Chebyshev-Padé型極點降階及傳輸線方程應用

劉 萌,苗 真,蔣耀林,

(1. 新疆大學數學與系統科學學院,新疆 烏魯木齊 830046;2. 西安交通大學數學與統計學院,陜西 西安 710049)

1 引言

隨著現代集成電路技術的快速發展,各類器件大規模集成化以及信號頻率不斷提高,大型或復雜動力系統仿真給工程技術人員帶來了巨大的挑戰。為了解決這個問題,必須給出新型的仿真方法來降低系統的復雜程度和分析難度,進而減少計算量,提高計算效率。這一背景下模型降階方法應運而生,其主要思想是用一個小規模的系統去近似原始大規模系統,降階系統在允許誤差范圍內保持系統輸入輸出特性的同時還要保持原始系統的穩定性、無源性等主要性質[1,2]。

在模型降階方法成體系出現之前,Padé逼近作為一種近似傳遞函數的方法,在數學領域已經被廣泛應用。以Padé有理逼近思想為基礎,進一步產生了漸近波形估計方法(AWE),它是一種顯式矩匹配方法[3],通過包含相對少量的主極點和零點的降階模型來近似傳遞函數。雖然電路可以產生大量的極點和留數,但在特定的頻率范圍內,所有的極點和留數的貢獻并不一定相等。瞬態響應通常可以由較少的主極點和留數控制,AWE方法可以提取這些主極點和留數,從而構建低階的傳遞函數,在合理精度內逼近電路的原始響應。這種方法只適用于較小規模的系統,其主要考慮降階系統如何保持系統的矩。文獻[4]提出了面向脈沖響應矩的計算方法,對大規模系統進行矩匹配過程提供了理論基礎。矩匹配類方法的基本思想是使降階后的傳遞函數匹配原始系統傳遞函數的前若干矩。針對單輸入單輸出系統,文獻[5]利用矩的概念研究了線性和非線性系統的模型降階問題。文獻[6]提出了一種獲得線性系統傳遞函數最優降階模型的新方法。它以迭代的方式使用多點Padé逼近來高效地生成最優模型。該方法通過將多個點的Padé逼近簡化為等價的Taylor級數來計算近似值。一維AWE的研究逐漸成熟,文獻[7]提出了M-D AWE方法,該方法將一維的AWE方法推廣至任意m維。一階極點AWE方法無法處理重復極點問題,文獻[8]將傳統的一階極點方法推廣到高階極點情形,提出了廣義AWE模型降階方法,對AWE方法進行了擴充。將有理逼近相關理論應用到模型降階領域當中,有助于提高模擬精度,例如,與經典Padé逼近相對照,Chebyshev-Padé逼近具有良好的整體逼近性質,且非常接近最佳一致有理逼近[9]。

本文在傳統AWE算法的基礎上提出Chebyshev-Padé型極點降階算法,使之能夠處理含重復極點的復雜問題,并進一步將其應用至傳輸線方程中。所提出的基本方法能夠在很少的降階階數下提高模型的近似精度。

2 Chebyshev-Padé型極點降階算法

本節主要介紹Chebyshev-Padé型極點降階算法,分別討論單重極點和多重極點情形。

考慮線性時不變系統

(1)

其中E,A∈Rn×n是常數矩陣,b∈Rn×1,c∈R1×n,x(t)∈Rn是系統的狀態變量,u(t)∈R是系統的輸入變量,y(t)∈R是系統的輸出變量。系統(1)經Laplace變換后滿足Y(s)=H(s)U(s)=c(sI-A)-1bU(s),其中Y(s)是y(t)的Laplace變換,U(s)是u(t) 的Laplace變換,H(s)表示系統的輸入輸出關系,即為傳遞函數。可簡記系統(1)為{E,A,b,c}。

2.1 Chebyshev多項式及其性質

定義1[9]多項式

Tn(x)=cos(narccosx),-1≤x≤1,n=0,1,…

稱為Chebyshev多項式。

性質1[9]Tn(x)=2xTn-1(x)-Tn-2(x),n=2,3,…

T0(x)=1,T1(x)=x

性質2[9]Tn是首項系數為2n-1的n次代數多項式,且T2k(x) 只含x的偶次冪,T2k-1(x)只含x的偶次冪。

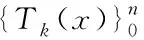
GT(x)=X

(2)

其中

(3)

2.2 Chebyshev-Padé型極點降階

對于線性時不變系統(1),將傳遞函數H(s)在s=0處做Taylor級數展開,可得

(4)

將傳遞函數H(s)在s=∞處進行Laurent展開,可得

(5)

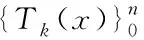
(6)

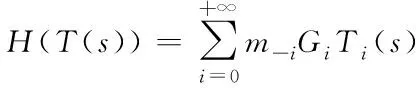
(7)

記Ci=miGi,C-i=m-iG(i=1,2,…)為廣義矩,其中Gi表示G的第i行。

用下述函數對原始系統進行有理逼近

(T(s))

(8)

(9)

(T(s))=1+b1T1(s)+…+bqTq(s)

(10)

(11)

(12)

上述降階過程可用算法1來描述。

算法1:Chebyshev-Padé型極點降階算法

輸入:線性系統{E,A,b,c},降階次數q

2) 將H(s)轉化為Chebyshev多項式

2.3 Chebyshev-Padé型逼近定理

為便于描述,下面簡記矩陣

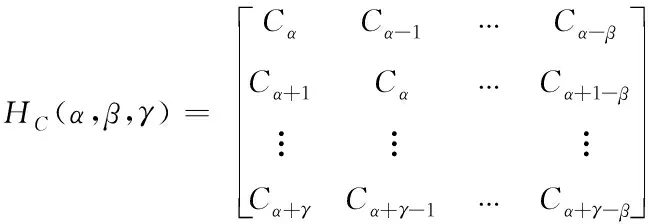
(13)

(14)

存在的充分必要條件是

rank{HC(L,M-1,M-1)}=rank{HC(L+1,M,M-1)}

(15)

證明:由于

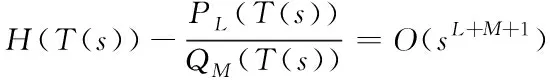
(16)

成立的充分必要條件是方程

QM(T(s))H(T(s))-PL(T(s))=O(s(L+M+1))

(17)

有解,令(17)式兩邊對應系數相等可得

(18)

進一步,方程(18)可改寫為

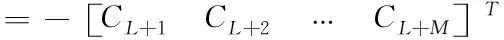
(19)

方程(18)和(19)的系數矩陣分別為HC(L+1,M,M-1)和HC(L,M-1,M-1),因此(17)式有解的充要條件為方程組系數矩陣和增廣矩陣具有相同的秩,即定理結論成立。

推論1 若矩陣HC(L,M-1,M-1)是非奇異的,則函數H(T(s))存在有理逼近式

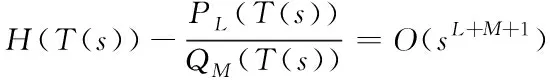
(20)

3 傳輸線系統的降階

本節將上述算法應用于傳輸線系統。傳輸線是一種導行電磁波結構,多導體傳輸線(MTL)的應用涵蓋了很寬的頻域范圍和各種傳輸線類型,從工頻輸電線路到微波電路。對于n+1個平行于z軸的導體構成的MTL,其傳輸線方程是一組耦合的2n個關于n個電壓Vi(z,t)和電流Ii(z,t) (i=1,2,…,n)的一階偏微分矩陣方程。大量的導體會產生巨大數目的耦合MTL系統,為了方便計算,需要降低結構的表征階數,用較少的有限個主導極點表示MTL傳輸函數[10]。

3.1 傳輸線模型

假設導體為理想導體,包圍在導體周圍的介質是均勻的,考慮傳輸線上的一個微分長度單元,可由單位長度電阻R,單位長度電感L,單位長度電導G,單位長度電容C對其進行描述。對傳輸線做出以下兩個假設:1)傳輸線的橫向尺寸在其長度方向上是連續的;2)傳輸線上的電磁波為準TEM波,即傳輸線上沿波傳輸方向的電磁分量遠遠小于其橫向分量。設i(x,t)與v(x,t)分別為傳輸線上x處的分布電流和分布電壓,根據基爾霍夫電壓定律KVL和基爾霍夫電流定律KCL可得如下傳輸線系統方程

(21)

其中R為電阻,L為電感,G為電導,C為電容。關于時間t做Laplace變換,可得

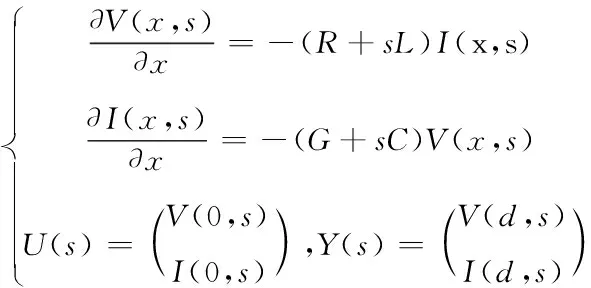
(22)

其中V(x,s),I(x,s),U(s),Y(s)分別表示,v(x,t),u(t),y(t)經過Laplace變換后的函數。可以將系統寫為如下矩陣形式

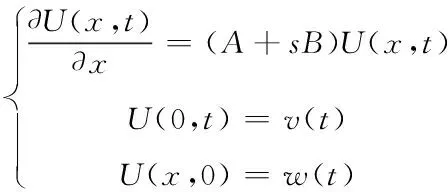
(23)

對傳輸線方程使用有限差分進行空間離散,將其轉化為狀態方程形式

(24)

其中

3.2 傳輸線模型的降階方法

對H(s)在s=0處做Taylor級數展開得

(25)

即Mi為系統的矩。對H(s)在s=∞處做Laurent級數展開得

(26)

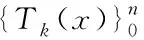
(27)

其中F(0)=F(s)|s=0是直流響應,且

(T(s))=a0+a1T(s)+…+aq-1Tq-1(s)

(T(s))=1+b1T(s)+…+bqTq(s)

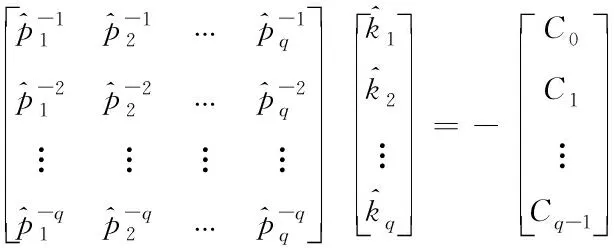
通過比較F(T(s))(T(s))=F(0)(T(s)) 中的項Ti(s)(i=q,q+1,…,2q-1)的系數,可得到如下線性方程組

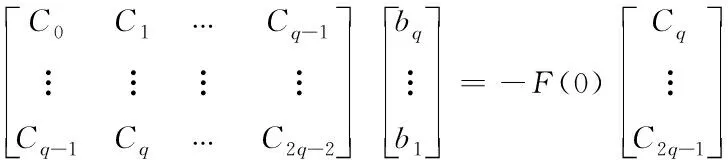
(28)

若pi≠pj(i≠j),將pj代入下式,得到關于kj(j=1,2,…,q)的線性方程組

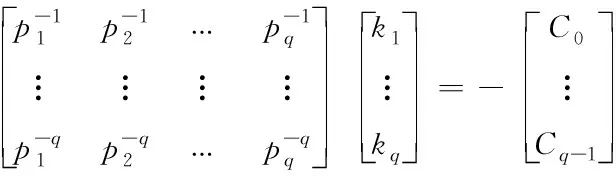
(29)

否則通過如下線性方程組求解出留數

4 數值實驗

為驗證本文算法的有效性,下面給出兩個數值算例。

例1 考慮如下的線性時不變系統

(30)

圖2 n=300,q=2時的系統輸出響應對比

由輸出響應對比圖可以看出n=300時,q=2的降階系統的輸出響應與原始系統的輸出響應曲線擬合程度更好。為了進一步表示算法的降階效果,在圖3、圖4中分別給出了基于Chebyshev-Padé型極點降階算法與傳統AWE的原始系統與降階系統的輸出相對誤差對比。

圖3 n=300,q=3時的系統輸出相對誤差

圖4 n=300,q=2時的系統輸出相對誤差

由相對誤差響應圖可以看出系統在較長時間模擬時,兩種算法均在q=2時的相對誤差更小。相比之下,Chebyshev-Padé型極點降階算法的相對誤差比傳統AWE更小。

例2 考慮一根半徑為rw=10mils,長l=1 m的導線位于無限大接地平面以上,距地高度h=2 cm。導線的電阻為5Ω,電感為L=3*10-4μH,電容為C=2.5*10-3μF。通過空間離散可得600階的傳輸線系統。分別采用Chebyshev-Padé型極點降階算法與傳統AWE,將上述傳輸線系統降至2階,得到如下結果。

圖5和圖6分別顯示了該傳輸線系統的傳遞函數在頻域上的幅值和相對誤差,可以看出將600階的傳輸線系統降至2階時,Chebyshev-Padé型極點降階算法的傳遞函數頻域幅值擬合效果良好,且擬合度相較AWE更高,具有明顯優勢。

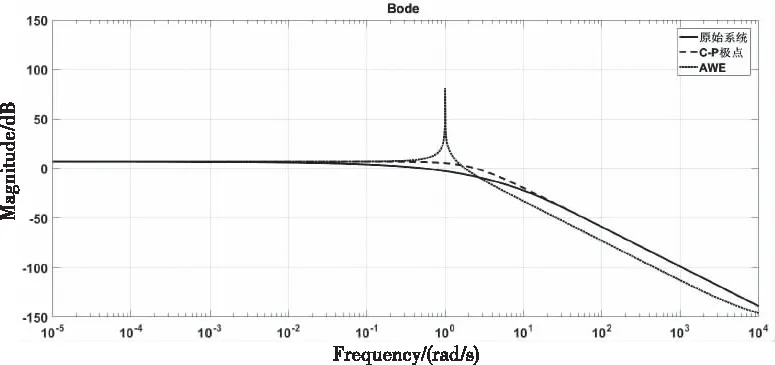
圖5 n=600,q=2時的傳遞函數幅值對比

圖6 n=600,q=2時的傳遞函數幅值相對誤差

5 結論

本文提出了Chebyshev-Padé型極點降階算法,通過將傳遞函數展開為Chebyshev級數,可以在匹配較少的廣義矩的條件下得到更為精確的降階系統。此外,根據傳遞函數的極點重數的不同情形可以通過Chebyshev-Padé型極點降階算法得到對應的留數,并進一步獲得傳遞函數和輸出響應。將該算法應用于傳輸線模型中,其數值結果表明降階系統能夠較好地近似原始系統。