電梯實驗臺的陪試電機加載算法研究與仿真

劉成源,韓震宇

(四川大學(xué)機械工程學(xué)院,四川 成都 610065)

1 引言

直升電梯是一種沿垂直導(dǎo)軌運行的箱體,利用電機進行升降運送人或貨物的特種機電設(shè)備[1]。由于其密閉的特點,一旦發(fā)生事故將會直接對電梯內(nèi)部人員造成嚴重傷害。數(shù)據(jù)調(diào)查顯示,2020年全國共發(fā)生25起電梯事故,因電梯自身故障的7起,共計造成19人傷亡[2],其中大多數(shù)事故都是電梯制動器失效而造成的沖頂或蹲底。為了保障使用者的人身安全,對電梯制動器的檢測顯得尤為重要。

目前對于制動力檢測,仍然使用GB 7588—2003《電梯制造與安裝安全規(guī)范》(下稱《規(guī)范》)[3]中定義的方法。該方法能夠?qū)崿F(xiàn)對電梯整機制動力的可靠檢驗,但是對于尚且未安裝到電梯井中的制動器無法做出可靠性評價。若使用《規(guī)范》中的方法將制動器安裝到電梯井中,不僅不便于操作,而且電梯井實驗設(shè)備造價和維護成本高,不利于整個行業(yè)的推廣。

由于《規(guī)范》中相關(guān)標準的缺失,目前對于制動器的獨立檢測尚且沒有形成統(tǒng)一的技術(shù)規(guī)范。目前趙海寧[4]等提出了對靜載荷制動能力性能指標的檢測方案與實驗設(shè)備,該種方案可以實現(xiàn)《規(guī)范》中對于靜力矩的制動需求,但不能對動態(tài)力矩進行檢測;而部分商家提供了制動器動態(tài)制動實驗,可以額外加載慣性力矩,但是測量再控制具有滯后性且力矩的輸出存在誤差,若根據(jù)t0時刻測量結(jié)果直接應(yīng)用到t1而不加以修正,將會帶來結(jié)果上的偏差;而謝小鵬等[5]和俞聲皋[6]等利用制動過程中動能與勢能的轉(zhuǎn)化關(guān)系,計算需要補償?shù)哪芰?填補理論上的缺陷,但在分析過程中直接忽略繩子重量,在面對高層建筑電梯繩子重量占比超過5%時,系統(tǒng)模型出現(xiàn)較大偏差。

為了解決上述文獻中存在的問題,本文提出了一種基于能量守恒的陪試電機力矩加載算法,通過分析制動過程的力學(xué)規(guī)律建立電梯的動力學(xué)模型,并利用運行過程中采集的加速度和轉(zhuǎn)矩,計算需要輸出的慣性力和額外補償?shù)霓D(zhuǎn)矩,在適當?shù)臅r候加載到系統(tǒng)中,實現(xiàn)使用電慣量的模擬。仿真表明,相較于現(xiàn)行方法,本算法不僅能夠有效模擬真實電梯的運行工況,而且能夠在一定范圍內(nèi)縮小力矩的輸出誤差,具有一定的抗干擾能力。

2 電梯物理學(xué)模型建立

常見的曳引式電梯的核心部件由曳引機、轎廂、對重塊、導(dǎo)向輪、曳引繩、補償繩和隨行電纜組成[7]。而出于安全性和舒適性的考慮,往往會安裝門系統(tǒng)、限位開關(guān)和彈簧緩沖器,此類非核心部件并不會顯著影響電梯的運行規(guī)律,因此在構(gòu)建物理模型時予以忽略。常見高層居民客用電梯的物理學(xué)簡化模型如圖1所示。

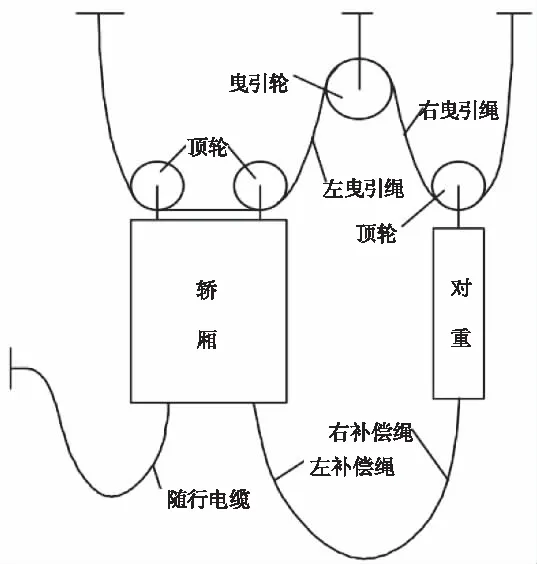
圖1 客梯簡化模型

3 電梯運行工況分析

電梯完成一次運行任務(wù)可簡單的使用S型速度曲線進行描述,在啟停階段都可以視為由曳引機控制的加減速運動。根據(jù)圖1所示的電梯簡化模型,假設(shè)曳引輪與曳引繩之間不發(fā)生相對滑動,對于曳引輪左側(cè)受力情況有

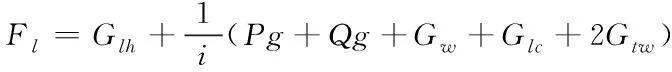
(1)

而曳引輪右側(cè)受力情況有

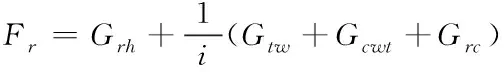
(2)

式中P為電梯轎廂質(zhì)量,kg;Q為電梯中的載荷質(zhì)量,kg;i為曳引比,1;R為曳引輪半徑,m;Gw為隨行電纜重量,N;Glc為轎廂補償繩(左補償繩)重量,N;Gtw為轎頂輪重量,N;Glh為轎廂曳引繩(左曳引繩)重量,N;Grh為對重塊曳引繩(右曳引繩)重量,N;Gcwt為對重塊重量,N;Grc為對重塊補償繩(右補償繩)重量,N。其中各部分繩子的重量由式(3)～(7)決定。

Glh=ρ1g(H-x)

(3)

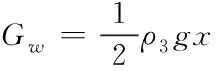
(4)

Glc=ρ2gx

(5)

Grh=ρ1gx

(6)

Grc=ρ2g(H-x)

(7)

其中H為轎廂最大提升高度,m;x為轎廂距地面高度,m;ρi分別為各繩子的線密度,kg·m-1。

當電梯位于不同樓層時,曳引輪兩端的偏載力矩由制動器提供的制動力抵消,此時偏載力矩為

M1=(Fl-Fr)R

(8)

代入以上各式有

2iρ1gH-Gcwt-ρ2gH)]R

(9)

當電梯在啟停過程中,曳引輪兩端會因為系統(tǒng)的加速度而產(chǎn)生額外的慣性力,對于常見的電梯,該部分慣性力是由轎廂、對重、轎廂中的載荷、各繩索的慣性以及各轉(zhuǎn)動部件的轉(zhuǎn)動慣量共同構(gòu)成。為了方便計算,將慣性折算到某回轉(zhuǎn)體中,由能量守恒定理和剛體轉(zhuǎn)動定理有[8]

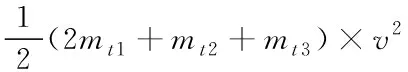
(10)

(11)

(12)

mt1=ρ1Hi

(13)

mt2=ρ2H

(14)

mt3=ρ3H

(15)

其中Js為直線部分等效后的慣量,kg·m2;mcwt為對重塊的質(zhì)量,kg;ws為等效后飛輪的角速度,rad·s-1;v為電梯轎廂的運行速度,m·s-1;D為曳引輪直徑,m;mt1為曳引繩質(zhì)量,kg;mt2為補償繩質(zhì)量,kg;mt3為隨行電纜的質(zhì)量,kg;ρ為繩子線密度,kg·m-1;H為電梯提升高度,m;Jd為回轉(zhuǎn)體的慣量,kg·m-2;wd為回轉(zhuǎn)體的角速度,rad·s-1;Jy、Jdw、Jtw分別為曳引輪、導(dǎo)向輪、轎頂輪的轉(zhuǎn)動慣量,kg·m2;wy、wdw、wtw分別為曳引輪、導(dǎo)向輪、轎頂輪的角速度,rad·s-1。

因此,可得到等效轉(zhuǎn)動慣量為直線部分慣性和轉(zhuǎn)動部分慣量之和,即

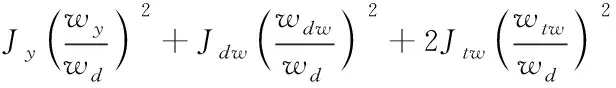
(16)

如圖1所示的電梯簡化模型,對其減速過程進行分析,則慣性力為[8]

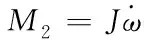
(17)

其中ω為系統(tǒng)曳引輪的角速度,J為系統(tǒng)等效慣量。

那么,對于制動過程中制動力M有

M-M1=M2

(18)

由上述計算可知,制動力矩是以高度x、載重量Q和角速度ω的三元函數(shù)。由于補償繩的存在,使得x前系數(shù)接近于0,在電梯系統(tǒng)中可以忽略由于高度不同而產(chǎn)生的力矩變化。考慮到Q和ω為線性疊加關(guān)系,對于選取不同常數(shù)參數(shù)的簡化系統(tǒng),在M1和M2同號取極限時,總力矩可以取得最大值。此時對應(yīng)著電梯過載下行和空載上行兩種極端狀態(tài),若制動力不足,電梯極易發(fā)生沖頂或墩底,因此需要對兩種狀態(tài)下的制動能力進行判定。

4 制動器制動力檢驗

4.1 檢驗設(shè)備

如圖2所示的是曳引機測試平臺的結(jié)構(gòu)示意圖,該平臺主要由陪試電機、減速器、轉(zhuǎn)矩轉(zhuǎn)速傳感器和被測曳引機等構(gòu)成。使用時由曳引機正常輸出轉(zhuǎn)矩,而使用陪試電機模擬輸出電梯轎廂、對重和載荷等所帶來的偏載轉(zhuǎn)矩和慣性力,在此期間,使用力矩轉(zhuǎn)速傳感器實時測量力矩和轉(zhuǎn)速用以反饋[9]。

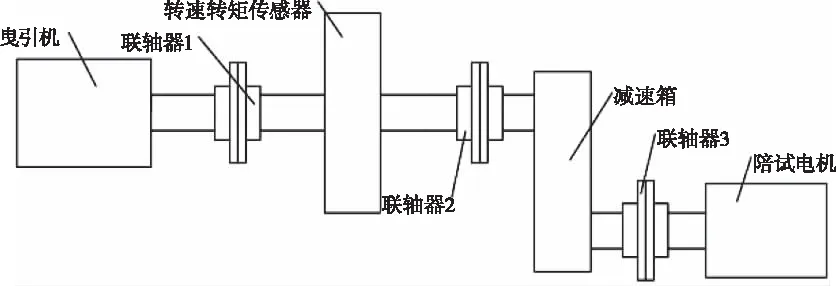
圖2 曳引機測試平臺

4.2 基于能量守恒的電機驅(qū)動方法

根據(jù)式(18)可知,減速過程中的制動力由恒定的偏載力矩和與加速度相關(guān)的慣性力矩構(gòu)成,在理論上只需要測量加速度值后,與理論加速度值進行比較便可得到下一時刻陪試電機需要補償輸出的力矩值。但在實際環(huán)境中,受制于電壓波動、溫升和負載波動等影響,偏載力矩的輸出無法保持恒定,理論值與實際值也并非相等。因此,需要對兩部分轉(zhuǎn)矩之和同時進行修正。

假定在一個電機控制周期內(nèi)傳感器能多次進行采樣且控制周期恒定,將整個制動過程劃分為n等分且步長為h,那么對于第i個周期的理論轉(zhuǎn)矩Mt(i)有[10]

Mt(i)=M1(i)+M2(i)+T(i)

(19)

其中T(i)為第i個周期內(nèi)需要補償?shù)霓D(zhuǎn)矩,M2(i)為使用上一個控制周期內(nèi)角加速度,即

M2(i)=Jαi-1

(20)

若假設(shè)第i個周期內(nèi)實際輸出的轉(zhuǎn)矩為Ma(i),則在第i周期內(nèi)轉(zhuǎn)矩差為

ΔM(i)=Mt(i)-Ma(i)

(21)

可以得到該周期內(nèi)的能量差為

(22)

該能量差需要在下一個周期內(nèi)進行補償,為保證總能量守恒有

(23)

考慮到在轉(zhuǎn)矩補償時無法提前獲知本周期內(nèi)的角速度,因此使用上一周期內(nèi)的角加速度估計本周期內(nèi)的角速度

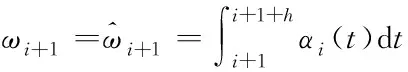
(24)

當控制周期h較小時,可以認為角加速度恒定,使用第i個周期內(nèi)速度的平均速度替代速度變化,則需要補償?shù)哪芰坎顬?/p>

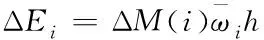
(25)

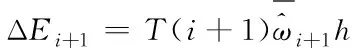
(26)

聯(lián)立式(25)和(26)則有i+1時刻增加的補償轉(zhuǎn)矩

(27)

綜上,可以得到每個控制周期所需要輸出的理論轉(zhuǎn)矩

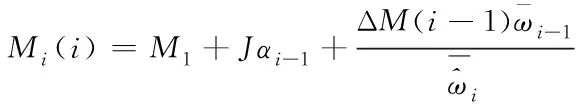
(28)

5 電機加載算法仿真

為了驗證該算法的可行性,需要獲知電梯在制動過程中的動能變化情況。如圖3所示,使用Adams建立電梯物理模型,其中最底端的兩輪僅為了方便建立模型且引導(dǎo)補償繩的走向,并無質(zhì)量和慣量,而隨行電纜質(zhì)量遠小于電梯總質(zhì)量,在模型中予以忽略。仿真中所使用的電梯模型數(shù)據(jù)如表1所示。

表1 電梯模型參數(shù)

圖3 adams仿真模型

使用上述數(shù)據(jù)模型進行仿真,使載荷為Q的電梯自頂層向下運行,當轎廂運行到額定速度且接近地面時制動器突然抱閘,采集制動過程中各部件的動能,并使用MATLAB處理后可得到系統(tǒng)的總動能如圖4所示,系統(tǒng)總動能最大值為4683.05 J。

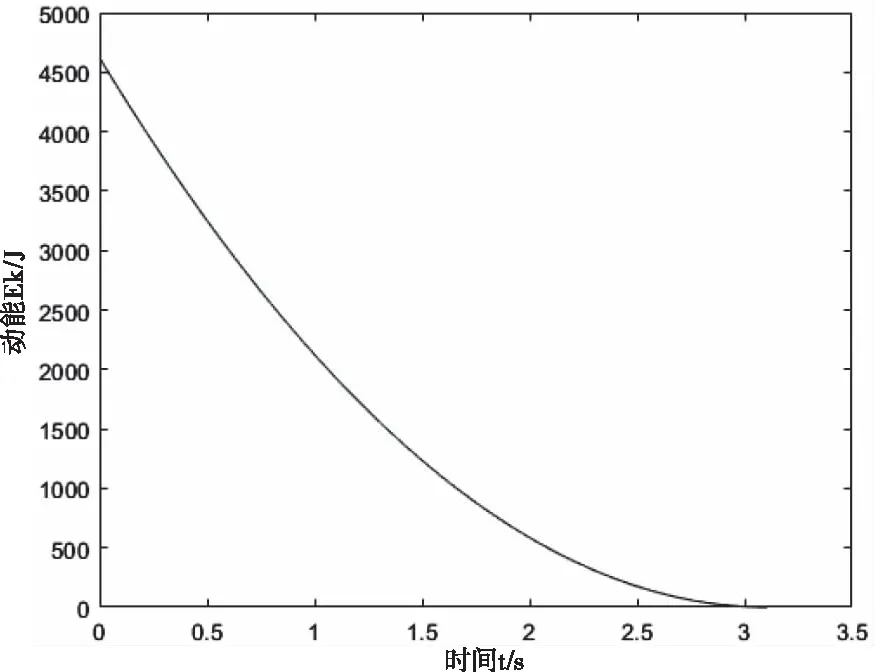
圖4 各部件總動能變化情況

基于圖2所示的實驗臺,使用MATLAB模擬制動器減速過程,對整體動能進行仿真檢測,驗證陪試電機加載算法的可行性。將折算慣量的回轉(zhuǎn)體定為曳引輪(安裝到曳引機輸出軸上),式(9)和(17)所提到的偏載轉(zhuǎn)矩和慣性力矩由本文提出的電機加載算法控制陪試電機進行輸出。假定陪試電機的控制周期為5ms,力矩速度傳感器采樣頻率滿足香農(nóng)采樣定理,力矩的實際輸出與理論輸出存在不超過1%的誤差。同時,使用現(xiàn)行商家提供的不補償?shù)目刂品椒ㄟM行比較,10次仿真結(jié)果如表2所示,其中一次的動能變化情況如圖5所示。

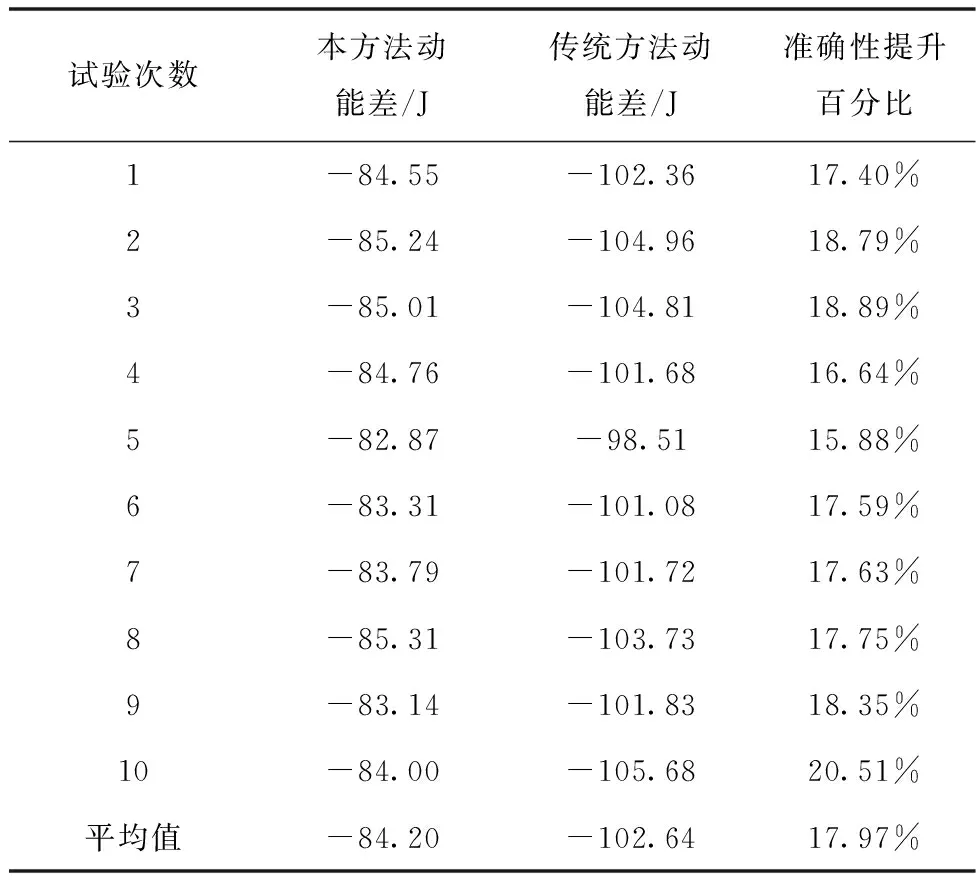
表2 力矩誤差為1%時仿真運行結(jié)果

可以看出,使用現(xiàn)行不補償?shù)姆椒ㄋ敵龅哪芰看笮〈笥诶碚撍枰膭幽?最終超出102.64J的能量,而本文的方法超出所需動能84.20J,輸出誤差為1.80%,力矩模擬的準確性提高17.97%。

將力矩的輸出誤差增大到5%,進行10次仿真結(jié)果如表3所示,其中一次的動能變化如圖6所示,現(xiàn)行不補償?shù)姆椒ǔ?26.49J,而本方法超出38.09J,輸出誤差為0.82%,力矩模擬的準確性提高69.88%,本方法依然能夠有效的控制輸出動能誤差。

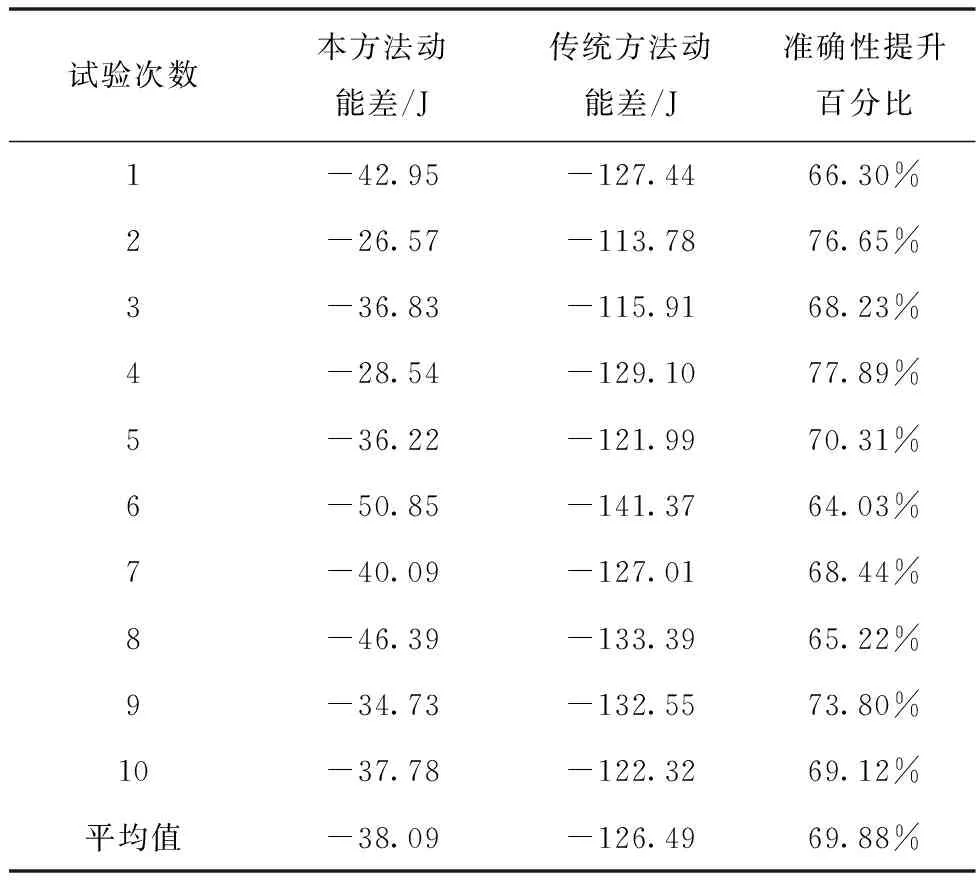
表3 力矩誤差為5%時仿真運行結(jié)果

圖6 誤差為5%時算法動能變化情況

根據(jù)兩次仿真誤差的趨勢也可以看出,隨著外界干擾的增大,現(xiàn)行檢測方法的動能跟隨誤差在逐漸增大,而本文方法的誤差在減小。基于能量守恒方法的陪試電機控制方法在力矩補償和誤差消除方面要優(yōu)于傳統(tǒng)的不補償方法。

6 結(jié)束語

本文通過對電梯的組成結(jié)構(gòu)和運行工況進行分析,得到了制動器在電梯制動過程中所受到的力矩的數(shù)學(xué)物理模型,針對現(xiàn)行制動力檢測方法中存在的力矩輸出滯后等問題,提出了一種基于能量守恒的陪試電機力矩補償算法。在力矩的實際輸出環(huán)節(jié)中加入隨機干擾,使用MATLAB對算法進行仿真并與利用Adams得到的電梯運行中的動能變化情況進行對比。仿真表明,與現(xiàn)行不補償?shù)姆椒ㄏ啾?本文提出的加載算法能夠有效的降低陪試電機輸出能量的誤差。但算法在面對較大電機輸出誤差時,不能完美跟蹤理論動能變化,存在制動時間縮短等與實際制動情況不符的現(xiàn)象,需要在未來的研究中不斷改進。