基于多懲罰因子優化VMD的滾動軸承故障特征提取方法

李 波, 胡哿郗, 石劍鈞, 劉恒暢, 洪 濤

(1. 電子科技大學航空航天學院, 四川 成都 611731; 2.飛行器集群智能感知與協同控制四川省重點實驗室, 四川 成都 611731)

0 引 言

滾動軸承因其摩擦阻力小、功率消耗小和機械效率高等特點,被廣泛應用于航空發動機[1-2]、鐵路運輸設備[3-4]以及大型工業機械設備[5-6],承擔動力傳遞和動力轉換的任務,是機械發生故障的主要故障源之一[7-8]。由于滾動軸承的健康狀態直接關系設備的安全穩定運行,因此及時發現關鍵滾動軸承中存在的故障,對確保機械安全穩定運行具有重大意義[9]。通常情況下,機械設備運行狀態的變化可通過其動態信號(例如振動信號)進行有效反映,利用信號處理技術分離出其中隱藏的故障特征信息。然而,其動態信號中蘊含了復雜機械結構中各個部件產生的信號成分,而且不可避免地存在背景噪聲,導致其中的故障特征信息被干擾成分淹沒。同時,滾動軸承復雜的工況使得動態信號表現出調頻、調幅等復雜的時變特性,提高了提取其故障特征信息的難度[10-11]。由于上述軸承工作環境的特點,如何在復雜噪聲環境下有效提取滾動軸承故障特征變得非常關鍵。

迄今為止,學者們提出了多種信號處理技術提取滾動軸承振動信號中的故障特征信息,而最有效的則是基于時頻域的信號處理技術。研究初期,小波變換被應用于滾動軸承的故障特征提取中,實現了對信號時頻變化特性的分析,但其變換效果極其依賴經驗選取的小波基函數[12]。為此,Huang等[13]首次提出了一種自適應時頻處理的經驗模態分解方法,合理解決了小波變換存在的“基選擇”經驗依賴問題,但其同時也存在端點效應和模態混疊的缺點。在此基礎上,Wu等[14]提出了集成經驗模態分解,有效地解決了經驗模態分解存在的模態混疊現象,但該方法存在一個白噪聲選擇問題,易出現分解效果不佳的情況。進而,Dragomiretskiy等[15]提出了變分模態分解方法,相比于集成經驗模態方法具有更好的信號局部性能和更優的噪聲抑制能力,但也存在分解過程中參數難以設定的缺點。

為了解決變分模態分解中參數難以確定的問題,學者們陸續開展了相應研究。王奉濤等[16]提出通過分解信號的能量差值來確定分解層數。畢鳳榮等[17]提出通過計算分解后各個本征模態函數(intrinsic mode function,IMF)的中心頻率差值來確定分解層數。李華等[18]提出通過最大峭度原則優化分解層數。然而,上述研究只優化了變分模態分解(variational mode decomposition, VMD)分解層數和懲罰因子中的一個,沒有全面考慮到這兩個參數之間的相互作用對分解效果的影響。為此,程軍圣等[19]以正交低峰值為優化目標函數,利用螢火蟲算法對分解層數與懲罰因子進行聯合優化。唐貴基等[20]提出以信號包絡熵作為粒子群算法的優化目標函數對參數進行優化。Xu等[21]引入Teager能量算子并結合最大峭度系數和平均峭度系數優化分解層數和懲罰因子。雖然上述研究實現了VMD分解層數與懲罰因子的自適應設定,解決了需手動設置參數的問題,但沒有考慮IMF各個分量對應的懲罰因子αk對VMD結果的影響。因此,鄭圓等[22]利用智能算法確定了分解層數和多懲罰因子αk,然而其在建立優化目標函數時,只考慮了分解后信號與原始信號的時域差異,無法有效地反映分解后信號包含原始信號的信息完整度。由此可見,當前利用VMD提取滾動軸承的故障特征時,其預先設置懲罰因子具有不確定性的問題并未得到合理解決,仍存在較大提升空間。

因此,本文提出一種基于多懲罰因子優化VMD的滾動軸承故障特征提取方法。首先,構建了融合皮爾遜相關系數、時頻譜相似度以及最大峭度值的優化目標,然后,通過最大峭度準則優化其分解層數,再利用灰狼優化(grey wolf optimization,GWO)算法獲取最佳分解層數以及最佳分解模態函數,保證了分解后模態函數最大限度地包含原始信號的故障特征信息,提升了滾動軸承振動信號經提取后故障特征的顯著性。最后,利用公開數據集分析驗證,通過對比多種不同方法,得出本文所提方法的故障特征提取效果優于其他同類方法,證明了該方法的有效性。

1 算法基本原理

1.1 VMD算法分解原理

VMD非遞歸式地將具有多個頻率成分的實信號分解為多個本征模態函數uk,并求得每個uk的單邊譜,同時對每個uk進行調頻,最后添加約束條件得到一個帶約束的變分模型[23]:

(1)

式中:ωk是假設分解得到的各階模態分量的頻率中心;uk是第k個IMF模態分量;f是原始信號;δ(t)為一脈沖函數。

通過拉格朗日函數將上述問題轉化為無約束變分問題[15]:

(2)

式中:α為懲罰因子;λ為拉格朗日乘子。再利用交替乘子方向算法求解,更新各IMF分量的中心頻率以及帶寬[15]:

(3)

(4)

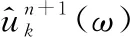
1.2 GWO算法原理

GWO算法將灰狼種群捕食活動中的追蹤、接近、圍捕以及進攻行為模擬運用到算法搜索尋優過程中,其種群將個體分為4個等級:α、β、γ和ω。通過前3種最好的個體α、β、γ引導群體向獵物方向(即最優解)靠近,該算法原理比較簡單。相比其他算法,在運算過程中需要調整的參數較少且比較容易實現,且收斂速度較快,收斂結果較準[23]。

灰狼種群追捕獵物的公式為

D=|C·Xp(t)-X(t)|

(5)

X(t+1)=Xp(t)-A·D

(6)

式中:C和A為系數;Xp(t)為獵物位置;X(t)為灰狼位置。C和A的更新公式為

C=2r2

(7)

A=2ar1-a

(8)

式中:r1和r2為隨機系數,其模值范圍為[0,1];a為收斂因子,隨迭代次數從2到0線性遞減。再由式(5)和式(6)求出3條頭狼的位置Xα(t+1)、Xβ(t+1)、Xγ(t+1),然后通過3條頭狼的位置確定種群中其他灰狼的位置:

(9)

GWO算法根據當前解空間中前3個最優解搜索全局最優解,同時在搜索過程充分借助輔助系數改變某個體權重,因此算法陷入局部最優的概率較低。

2 基于GWO-VMD的滾動軸承故障特征提取方法

2.1 基于皮爾遜相關函數、最大峭度和時頻譜相似度的優化目標函數

原始信號分解后的信號不能丟失原始信號的關鍵信息特征,且分解后的信號應更明顯地體現出其內部的特征,否則做此分解操作并無意義。因此,量化分解效果的有效性應有兩個準則[24-26]:一是分解后的信號應盡量包含原始信號完整信息;二是分解后應更明顯地突出故障特征。

基于上述兩個準則,本研究提出3個優化目標:皮爾遜相關系數、時頻譜相似度以及最大峭度。

(1) 皮爾遜相關系數

皮爾遜相關系數可衡量兩種信號的線性相關程度,絕對值越大代表線性相關的程度越強。

首先將信號進行VMD,然后通過得到的模態分量將信號重構,得到重構信號X(t),Xi為重構信號X(t)某一個樣本點。設原始信號為S(t),Si為原始信號S(t)某一個樣本點,則可計算X(t)和S(t)的皮爾遜相關系數如下:

(10)

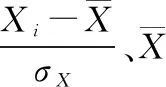
(2) 時頻譜相似度

時頻譜能夠描述兩種信號在時域上其頻率成分的變化情況,恰好解決了非平穩信號在時域上其頻率不斷變化的問題,通過時頻譜相似度可以有效地反映兩種非平穩信號的相關性。

利用希爾伯特黃變換求得重構信號時頻譜Xt-f和原始信號時頻譜St-f,其時頻譜相似度為

(11)

(3) 最大峭度

峭度是一種無量綱參數。通常情況下滾動軸承振動信號峭度值為3左右,信號幅值呈正態分布,當出現故障時,振動信號峭度值增大且信號幅值偏離正態分布。峭度值越大,表明該滾動軸承故障越嚴重。

當原始信號分解后,其各個模態分量中的最大峭度越大,說明分解后的信號故障特征變現越明顯,因此計算分解后各個本征模態分量的峭度,取最大的峭度:

(12)

兩個時域信號的皮爾遜相關系數只能表征兩個信號時域上的相關性,且在此背景下,皮爾遜相關系數只有正向判定而無反向判定,即數值高表征兩個信號高度相似,但數值低并不能表征兩個信號毫無相關性。因此,求得以上3個指標后,引入閾值融合皮爾遜相關系數、時頻譜相似度和最大峭度,融合流程圖如圖1所示。

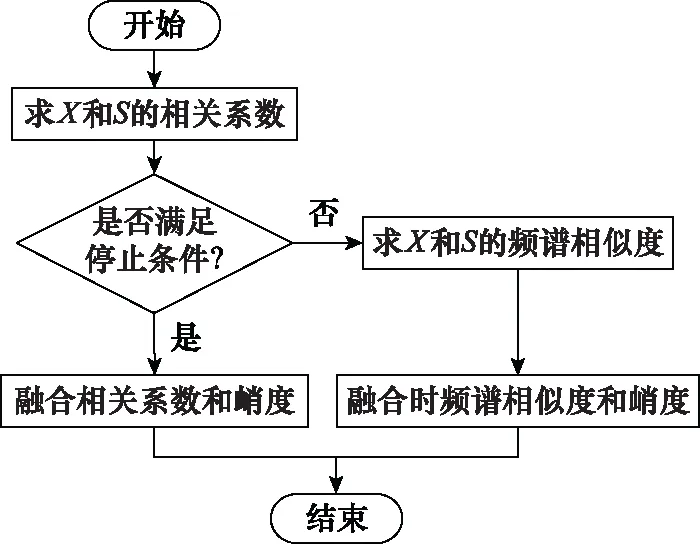
圖1 融合3個目標流程圖

如圖1所示,當兩種信號的皮爾遜相關系數大于某閾值時,則可充分表明重構信號包含原始信號的完整信息特征,因此融合最大峭度系數,提高其對故障特征的敏感性,不必再進行大量的計算求得時頻譜相似度。當皮爾遜相關系數小于閾值,此時皮爾遜相關系數失效,必須求得時頻譜相似度來標定重構信號與原始信號的相關性。

2.2 基于GWO-VMD的滾動軸承故障特征提取方法

在VMD算法中懲罰因子α是一個重要的參數,其決定著VMD后各IMF的帶寬。通常,滾動軸承的振動信號包含諧波分量與脈沖分量,諧波信號頻帶帶寬較小,因此VMD時需要較大的α,有利于提取其特征;而故障脈沖信號相反,其時域較短,頻帶帶寬較大,因此VMD時需要較小的α,有利于提取其特征。

由此可見,單懲罰因子VMD無法同時提取滾動軸承振動信號包含的諧波特征與故障脈沖特征。因此,本文首先利用最大峭度準則優化VMD的分解層數K,然后通過GWO算法,以上文的優化目標函數為適應度,為每個IMF分量搜尋最優的懲罰因子,信號經分解后,對各個本征模態分量作包絡譜分析,提取其故障頻率特征。算法具體流程圖如圖2所示。

算法具體步驟如下所示。

步驟 1首先需要確定分解層數K的值,設置K從2遞增到n,每次迭代中對振動信號作VMD得到K個模態分量,分別求得每個本征模態分量的峭度值,并取最大值,取第一個達到極大值時對應的K。

步驟 2設置GWO初始參數a,A、C的值。

步驟 4將每只灰狼的位置Xi作為懲罰因子[α1,α2,…,αK]對信號進行VMD,根據式(10)～式(12)計算得出適應度值,并記錄最優的3個頭狼個體位置Xα、Xβ和Xγ。

步驟 5通過式(9)更新其他灰狼個體的位置,并通過式(7)和式(8)更新參數A、C和a的值。

步驟 6循環執行步驟4和步驟5,直至迭代完畢。

步驟 7選取適應度值最大的個體作為優化后的懲罰因子[α1,α2,…,αK]以及最佳分解層數K作為VMD參數對信號作分解。

步驟 8對各個IMF做包絡解調,提取故障特征信息。

3 實驗與分析

3.1 數據源選擇

本實驗數據來源于某電氣工程實驗室的滾動軸承數據,是相關研究學者普遍采用的數據集。該實驗采用一個參數可調節的電機作為負載,負載可為1 hp、2 hp以及3 hp。實驗中的故障類型為表面加工的單點故障。實驗中被測試的軸承有兩種,其中SKF型號軸承的故障直徑包含0.007 mils、0.014 mils、0.021 mils,NTN型號軸承的故障直徑包含0.028 mils以及0.040 mils。本研究選擇了故障直徑為0.021 mils的SKF型號軸承振動信號數據來驗證所提方法的有效性,其轉速為1 772 r/min,采樣頻率為12 kHz。

3.2 實驗過程與結果分析

首先,根據模型算法求得最佳分解層數,固定分解因子,計算出不同分解層數對應的最大峭度值,最大峭度與分解層數的關系圖如圖3所示。由圖3可以觀察到,最大峭度值對應的分解層數為4,因此最佳分解層數為4層。求出最佳分解層數后,運用GWO-VMD算法,為每層模態求得最佳的懲罰因子。

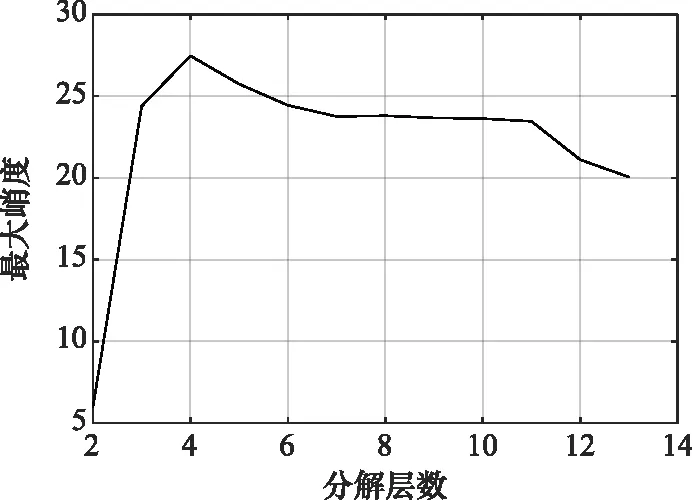
圖3 最大峭度與分解層數的關系

本實驗還將本算法與基于參數優化的VMD(parameter optimized VMD,PO-VMD)、基于蝗蟲優化算法的VMD(grasshopper optimization algorithm-VMD, GOA-VMD)兩種算法求解最優值的收斂情況進行對比,3種算法的收斂迭代折線圖如圖4所示。從圖4中可觀察到,GWO-VMD算法收斂效果最好,在47代左右基本收斂達到最優值;PO -VMD算法雖在前期收斂較快,但最終在70代左右才基本收斂達到最優值;GOA-VMD算法的效果則完全不如GWO -VMD算法。表1為各算法達到最優值的收斂情況,可觀察到雖然PO-VMD算法可達到最快的收斂速度,但其整體性能遠遠不如GWO-VMD算法,而GOA-VMD算法各項指標都不如GWO-VMD算法,因此可表明GWO-VMD算法的效率性強于其他算法。由算法求得4層對應的懲罰因子分別為[5 224, 4 110, 1 860, 540]。

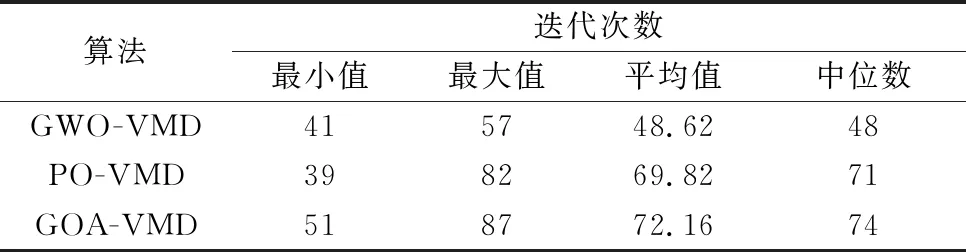
表1 3種算法收斂情況

將上述求得的最佳分解層數和懲罰因子代入,對信號作VMD,并通過分解后的各個模態分量重構原始振動信號數據如圖5和圖6所示。由圖5和圖6可觀察到,原始信號與重構信號的時域波形及其相似。對這兩種信號作包絡解調,如圖7所示,可觀察到原始信號與重構信號的包絡譜圖極其相似,重構信號包絡譜圖僅僅在某些頻率上的幅值有些許損失,因此表明該重構信號包含原始信號的完整特征,證明了該方法的有效性。

圖5 原始振動信號波形圖

圖6 重構信號波形圖

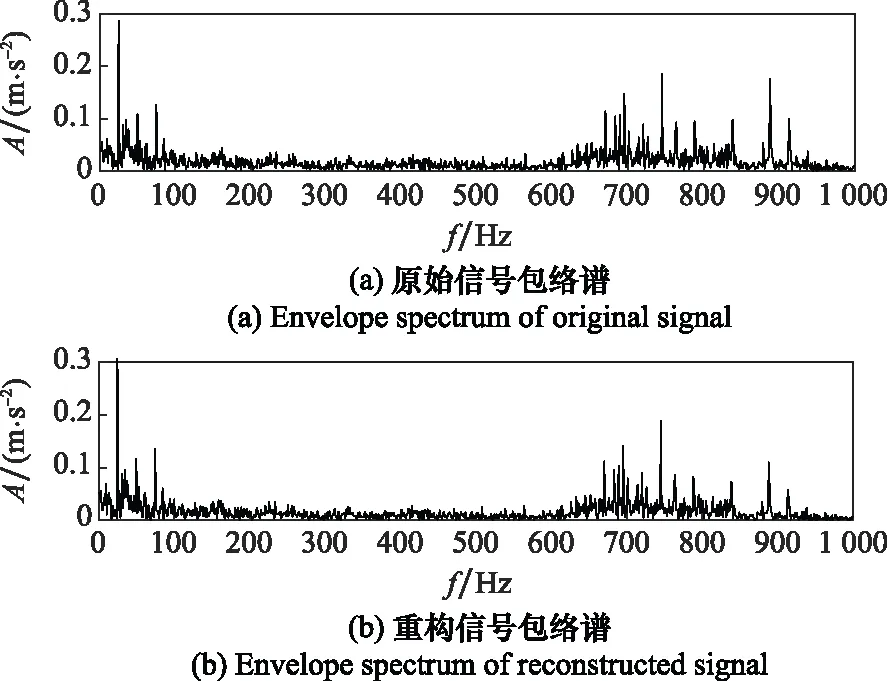
圖7 原始信號與重構信號包絡譜

再進一步對信號作分解,并求出各個IMF分量的頻譜圖。GWO-VMD算法分解后各個IMF的時域波形圖以及對應的頻譜圖如圖8所示。可觀察到,原始信號通過分解后,分離出了各個頻段部分的分量,分解效果較好。PO -VMD算法和VMD算法分解各分量時域波形和頻譜分別如圖9和圖10所示。可以觀察到,圖9中IMF2的頻譜圖與IMF4頻譜圖處有重疊,并且在低頻處丟失了信號應有的頻率特征。圖10也有相似的特點,圖10中IMF1的頻譜圖與IMF4的頻譜圖處有重疊,也丟失了信號本該有的低頻特征,這證明了本文方法的有效性以及優越性。

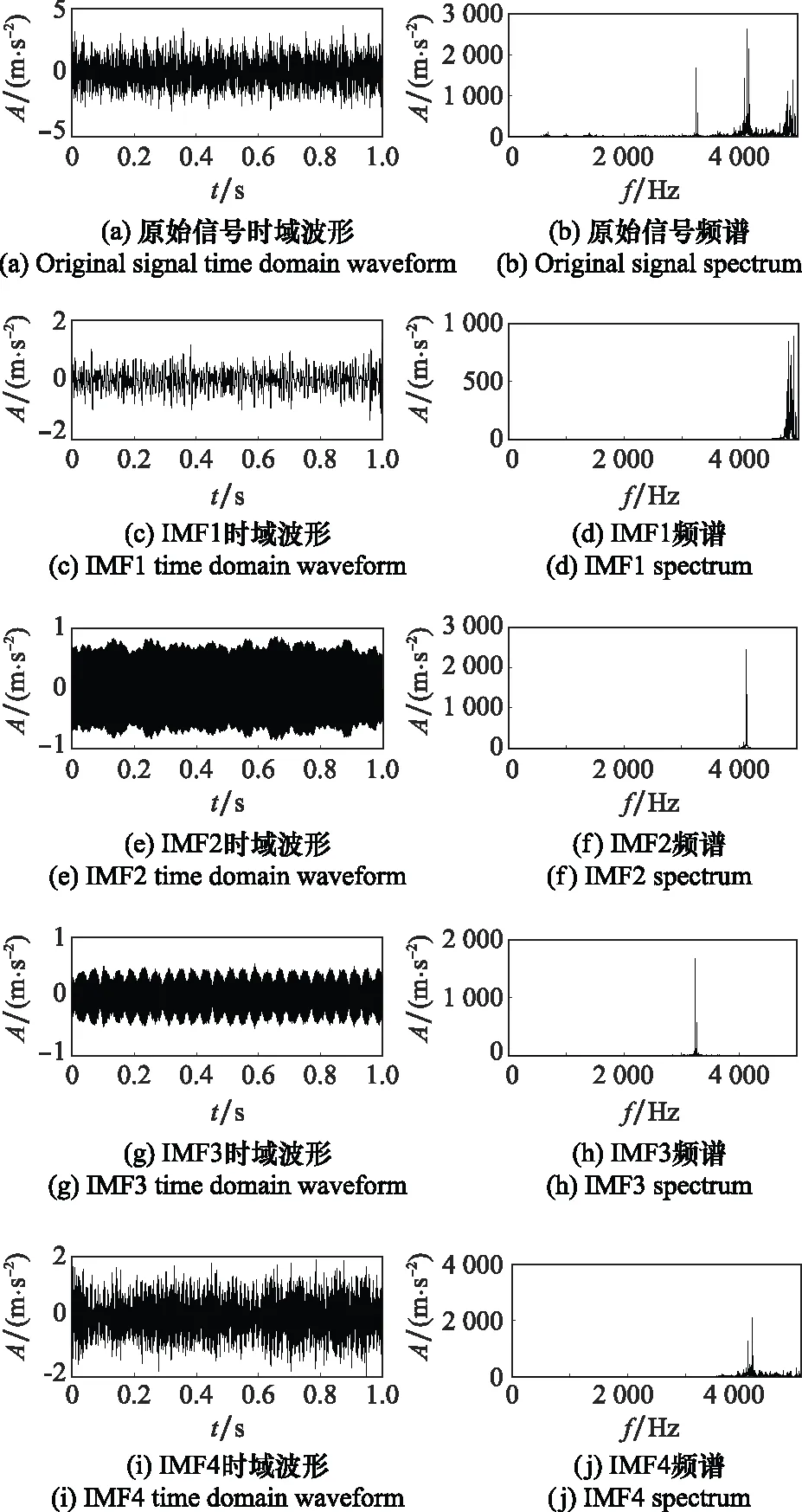
圖9 PO-VMD各分量時域波形和頻譜

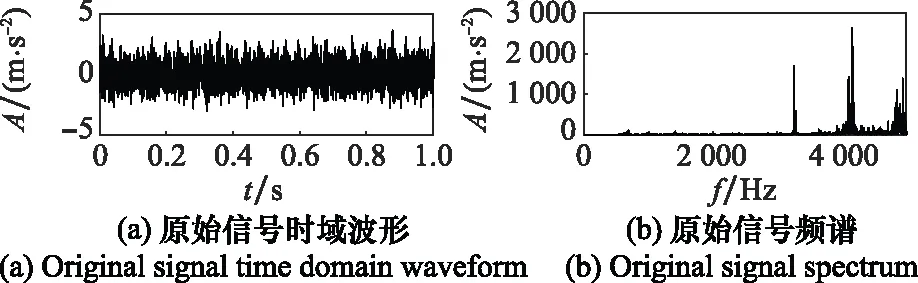
圖10 VMD各分量時域波形、頻譜

然后,再對3種算法分解得到的IMF分量作包絡解調,得到各個IMF分量的包絡譜圖。GWO-VMD后各IMF的包絡圖如圖11所示。可以看到,在故障頻率處以及其2～5倍頻處有明顯的譜峰,說明提取到了其故障特征頻率,證明本文提出方法的有效性,并且譜圖在故障頻率及其倍頻處比較干凈,干擾較少。

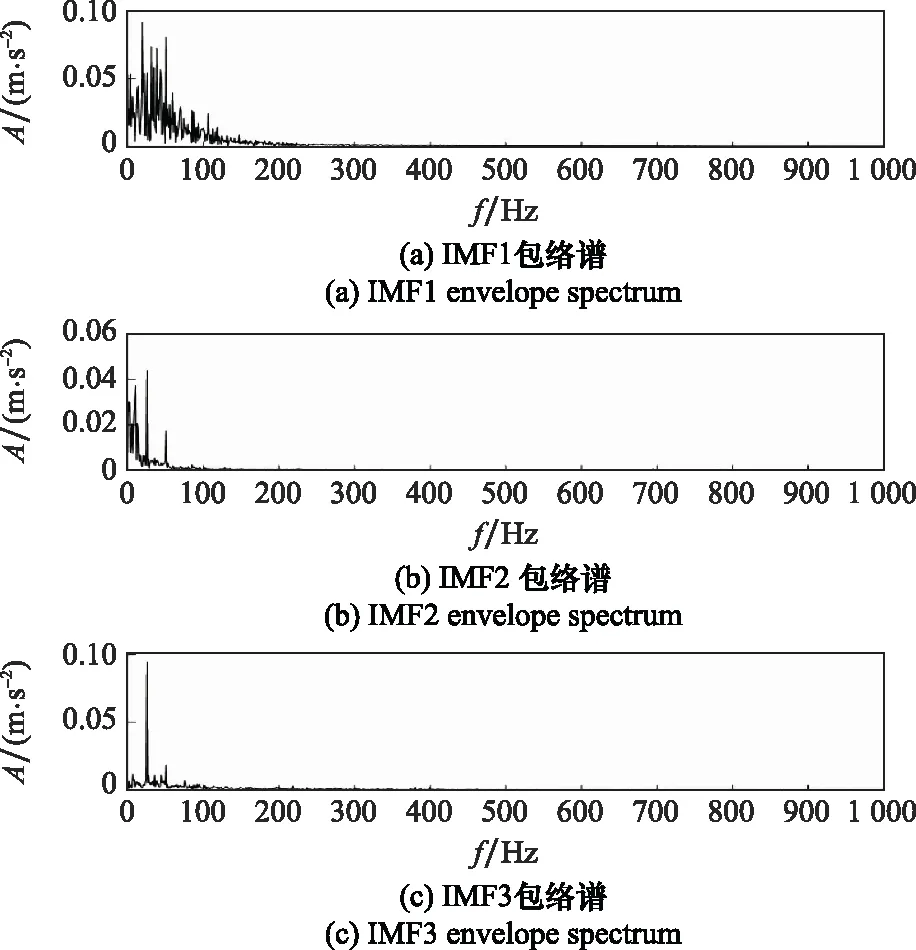
圖11 GWO-VMD后4個IMF的包絡譜

PO-VMD后的各IMF包絡譜圖如圖12所示。從圖12可以觀察到,通過PO -VMD后,雖在IMF4包絡譜圖中在故障特征頻率處以及其2～3倍頻處有譜峰,但是其譜峰不是很明顯,受周圍噪聲頻率干擾會比較大,并且在4倍頻以及4倍頻以上處基本看不到譜峰,抑制效果過于嚴重導致所需要的故障特征也被抑制,無法有效地表征信號中蘊含的故障特征信息。

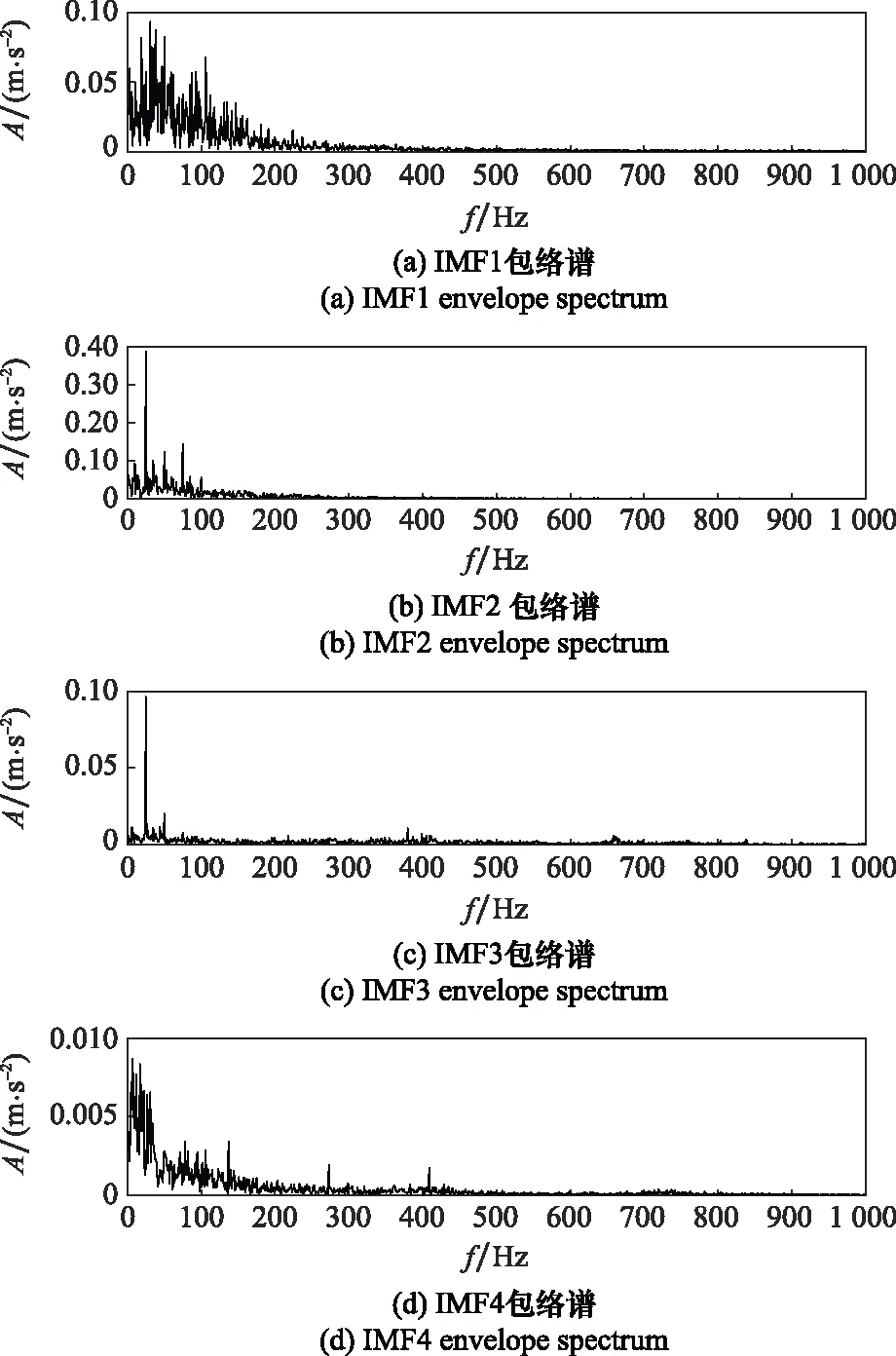
圖12 PO-VMD后各IMF的包絡譜

VMD后的各IMF包絡譜圖如圖13所示。從圖13可觀察到,VMD后各個IMF都出現了較大的噪聲,分解過程中噪聲抑制不明顯,并且分解后頻率成分幾乎集中在低頻中,該頻段噪聲干擾很大,無法有效地觀察到故障頻率特征。

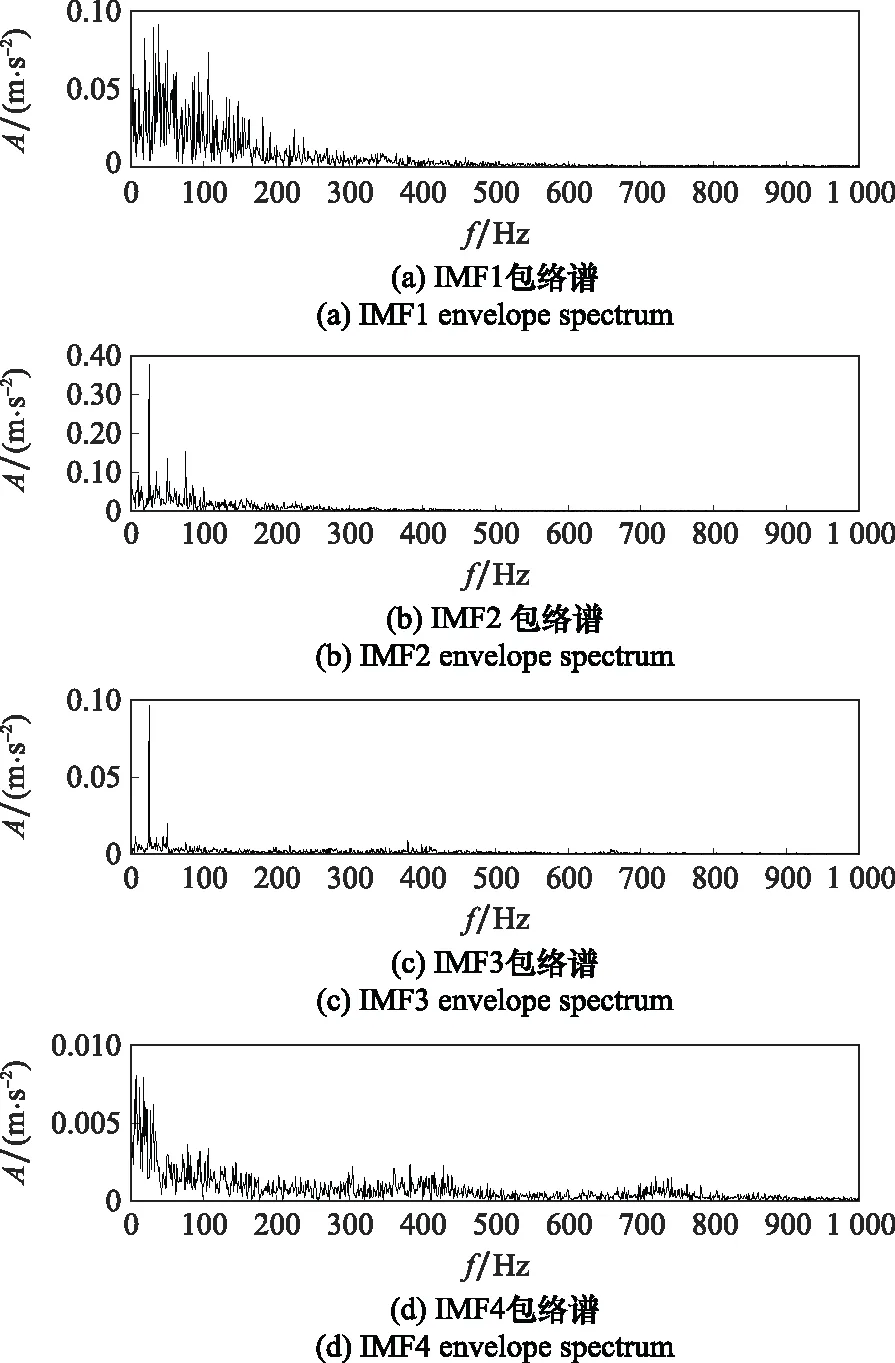
圖13 VMD后各IMF的包絡譜

上述分析結果表明了本文方法提取效果更好,能夠更有效地提取出故障特征頻率。表2中列出了3種方法提取的特征頻率幅值情況,并做了歸一化方便對比。同時,從表2也可以觀察到本文所提的GWO-VMD方法提取的特征頻率幅值遠大于其他兩種對比方法,進一步驗證了本方法的有效性和優越性。

表2 3種算法提取特征頻率幅值

4 結 論

本文提出了一種基于多懲罰因子優化VMD的滾動軸承故障特征提取方法,該方法以VMD理論為基礎,以提升故障特征顯著性和包含信息完整性為目標,構建融合皮爾遜相關系數、時頻譜相似度以及最大峭度值的優化目標函數,并利用GWO算法自適應地搜索VMD的最佳分解層數和每個IMF分量對應的懲罰因子,解決了VMD需根據經驗手動設置參數導致分解效果不佳的問題,實現了滾動軸承故障特征的有效提取。實驗結果分析表明,GWO-VMD與PO -VMD和VMD等算法相比,可以在噪聲環境下有效地提取軸承故障特征。