構造長度為4ps的量子重根循環碼

汪余婷, 劉 麗

(合肥工業大學 數學學院,安徽 合肥 230601)

0 引 言

自文獻[1]和文獻[2]提出量子糾錯碼以來,量子碼的相關研究開始受到關注。量子糾錯是量子計算和量子通信得以實現的重要保證,是信息科學的一個重要組成部分;循環碼作為經典糾錯碼中的重要環節,在量子糾錯方面具有重要作用。本文主要研究的是Fq上碼長為4ps的重根循環碼,并利用它們構造量子碼。

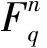
本文基于Steane擴展構造,給出Fq上線性碼C為自正交碼的條件,構造幾類參數較好的非二元量子碼。根據在Fq上碼長為4ps的重根循環碼的最小漢明距離以及對偶包含的關系,確定自正交碼的條件;根據Steane擴展構造的相關內容,構造幾類參數較好的量子碼。

1 基礎知識

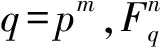
眾所周知,Fq[x]/〈xn-1〉的任一個理想都是主理想,即C=〈g(x)〉,其中g(x)是首一的且滿足g(x)|(xn-1),被稱為生成多項式。碼C的對偶定義為:

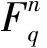
長度為n維數為k的q進制量子碼是希爾伯特空間H=Cqn=Cq?…?Cq的子空間。設|x>是Cq的正交基且x、a、b∈Fq。在Cq上,定義X(a)|x>=|x+a>和Z(b)|x>=ωtr(bx)×|x>,其中tr是從Fpm到Fp的跡映射,且ω=exp(2πi/p)是p次本原單位根。

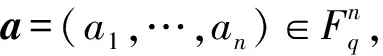
X1(a)=X1(a1)?X1(a2)?…?X1(an),

X2(a)=X2(a1)?X2(a2)?…?X2(an),

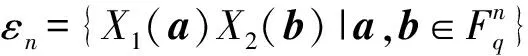
若C是[[n,k,d]]q量子碼,則k≤n-2d+2,稱該界為量子Singleton界;若量子碼C的參數滿足k=n-2d+2,則稱C為量子最大距離可分(maximum distance separable,MDS)碼。

2 長度為4ps重根循環碼的漢明距離

設C是Fq上碼長為4ps的循環碼,則C是環R=Fq[x]/〈x4ps-1〉的一個理想。

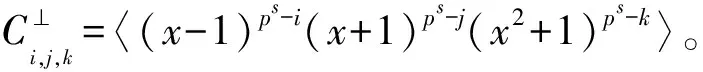
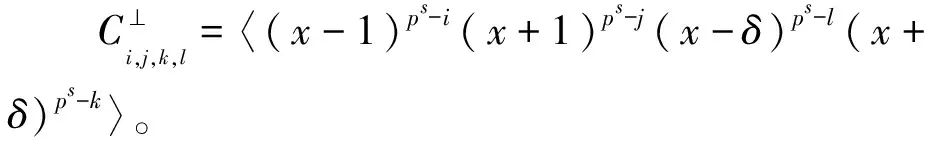
下面給出Fq上碼長為4ps的循環碼包含其對偶碼的充要條件。

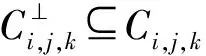
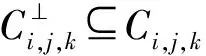
結合文獻[26]給出的Fpm上碼長為4ps的最小漢明距離,對偶包含碼的漢明距離見表1～表3所列。

表1 對偶包含碼Ci,j,k的漢明距離

3 構造量子碼

本節根據長度為4ps的重根循環碼構造幾類量子碼。

定理2 設q是奇素數p的冪次,若s≥2或p≥5且s=1,則存在一個參數為[[4ps,4ps-ps-1-4,3]]q的量子碼。

證明考慮Fq上碼長為4ps的循環碼

Ci,j,k=〈(x-1)i(x+1)j(x2+1)k〉,

其中:i=ps-1+1;j=0且k=1。

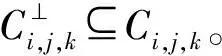
例1設q=p≥5且s=1,則存在一個p元參數為[[4p,4p-5,3]]q的量子碼。由量子Singleton界可知,這是一個碼長為4p且最小距離為3的q元量子碼,其維數是4p-4。經驗證,這是一個參數較好的量子碼。

定理3設q是奇素數p的冪次,若s≥2或p≥7且s=1,則存在一個參數為[[4ps,4ps-3ps-1-6,4]]q的量子碼。

證明考慮Fq上碼長為4ps的循環碼

Ci,j,k=〈(x-1)i(x+1)j(x2+1)k〉,

其中:i=2ps-1+1;j=0且k=1。

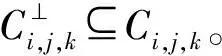
例2 設q=p≥7且s=1,則存在一個p元參數為[[4p,4p-9,4]]q的量子碼。由量子Singleton界可知,這是一個碼長為4p且最小距離為4的q元量子碼,其維數是4p-8,是一個參數較好的量子碼。

定理4 設q是奇素數p的冪次,且q≡1(mod 4),若s≥2或p≥5且s=1,則存在一個參數為[[4ps,4ps-ps-1-3,3]]q的量子碼。

證明考慮Fq上碼長為4ps的循環碼

Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,

其中:δ2=-1;i=ps-1+1;j=l=0且k=1。

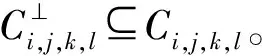
例3設q=p≥5且s=1,則存在一個p元參數為[[4p,4p-4,3]]q的量子碼。由量子Singleton界可知,這是一個碼長為4p且最小距離為3的q元量子碼,其維數是4p-3,是一個參數較好的量子碼。

定理5 設q是奇素數p的冪次,且q≡1(mod 4),若s≥2或p≥7且s=1,則存在一個參數為[[4ps,4ps-3ps-1-5,4]]q的量子碼。

證明考慮Fq上碼長為4ps的循環碼

Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,

其中:δ2=-1;i=2ps-1+1;j=k=1且l=0。

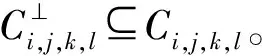
表2 0≤l≤j≤k≤i≤ps時對偶包含碼Ci,j,k,l的漢明距離

例4設q=p≥7且s=1,則存在一個p元參數為[[4p,4p-8,4]]q的量子碼。由量子Singleton界可知,這是一個碼長為4p且維數是4p-8,其最小距離最大為5的q元量子碼,因此是一個近似MDS碼。

定理6 設q是奇素數p的冪次,且q≡1(mod 4),若s≥2或p≥7且s=1,則存在一個參數[[4ps,4ps-ps-1-6,3]]q的量子碼。

證明考慮Fq上碼長為4ps的循環碼

Ci,j,k,l=〈(x-1)i(x+1)j(x-δ)k(x+δ)l〉,

其中:δ2=-1;i=2ps-1+1;j=k=1且l=0。

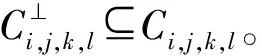
表3 0≤l≤k≤j≤i≤ps時對偶包含碼Ci,j,k,l的漢明距離

例5 設q=p≥7且s=1,則存在一個p元參數為[[4p,4p-8,3]]q的量子碼。由量子Singleton界可知,這是一個碼長為4p且維數是4p-8的q元量子碼,其最小距離最大為5的q元量子碼,因此是一個近似MDS碼。

5 結 論

本文在Fq上碼長為4ps重根循環碼的基礎上,基于Steane擴展構造,構造了幾類極小距離、維數等參數均有改進的非二元量子碼。利用循環碼的其他碼長來構造新的參數較好的量子碼是進一步可以研究的問題。