基于粒子群優化算法的模型超參調優方法應用研究

鐵錦程 趙戰營

(上海浦東發展銀行 上海 200120)

0 引 言

大數據、人工智能、云計算等技術的發展,推動著每一家金融機構探索科技創新賦能業務增長。ABCD(AI人工智能、Blockchain區塊鏈、Cloud Computing云計算、Big Data大數據)是金融科技創新發展的核心技術,金融行業良好的信息化建設與規范的大數據資源管理,為人工智能在獲客、風控、營銷等領域應用落地打好了堅實的基礎。數據是金融發展的重要戰略資源,數據驅動信用卡業務的發展,迫切需要提升數據價值應用的效率和效果,機器學習技術通過AI算法對歷史樣本數據進行學習,生成對未來的數據進行預測的模型,廣泛應用于獲客、營銷、風控、合規、消保等信用卡經營管理業務。

機器學習模型是數據價值應用的有效手段,然而數據和特征決定了機器學習效果的上限,而模型算法決定了逼近這個上限的程度。機器學習模型的性能與超參數直接相關,如何在現有數據特征的基礎上,提高機器學習模型的效果很大程度上取決于模型超參數調優(Hyper-Parameters Optimization,HPO)。超參調優是機器學習工作流中最難的工作,多組可調整參數構成的高維連續數值空間中存在海量的參數組合,每次調整后,都需要利用訓練得到的模型的準確率和泛化能力作為參數調優的評價標準[1]。人工調參是一種反復試驗的方法,需要消耗大量的時間,所得到的結果也無法保證是最佳的參數組合,因此誕生了很多自動化超參數優化的方法。本文提出基于粒子群優化算法的模型超參數調優方法,通過設置偏移量、慣性系數、個體學習因子和群體學習因子等超參數初始值,隨機選定若干組模型參數組合生成初始粒子群,通過動態更新慣性系數和偏移量來動態更新模型參數組合,不斷循環迭代,直至模型參數近似最優。通過對比實驗驗證,與常用的網格搜索、隨機搜索、貝葉斯優化等調優方法相比,本文提出的基于粒子群優化算法的模型超參數調優方法能夠提高調參效率,在相同的樣本集上使用該方法進行模型參數調優,通過多輪迭代逐步逼近最優解,更容易達到預期的模型效果目標,能夠提升機器學習模型的預測精度和泛化能力。

1 模型超參數優化問題研究

1.1 模型超參數優化及其重要性

隨著互聯網、大數據、人工智能技術的發展,新生信息層出不窮,知識總量爆炸式增長,為數據價值的挖掘提出了新的挑戰,機器學習能夠發現和挖掘數據規律,并應用于對未來的預測,實現數據價值驅動業務增長。然而,機器學習模型的開發和應用,既需要對業務的深入理解,又需要統計、算法理論分析等知識技能,門檻相對較高、流程較為繁瑣。業務分析人員完成模型定義之后,機器學習模型的開發應用主要涉及如下五個階段,如圖1所示。

機器學習算法模型的參數包含模型參數和超參數兩類,模型參數是在訓練過程中可進行自動優化或學習得到的參數,不需要手動設置;超參數是在模型訓練之前設置的,用于控制模型擬合數據的靈活性,無法通過數據學習得到,需要用戶手動配置[2]。在機器學習模型開發應用涉及的主要階段中,超參數優化的目的是對模型超參配置進行調優,使得訓練產出的模型具有較好的業務效果、穩定性和泛化能力。模型超參數優化是一項繁瑣但至關重要的任務,直接決定著模型效果的優劣,很大程度上影響了算法的性能。一個機器學習模型中,一般有著多個超參數,每個超參數可調整的數值范圍是非常廣的,也就是說,參數調優是在多維連續數值空間內,找到最優的一組參數組合,使模型效果最優。這個難度是非常大的,且不同機器學習模型的超參數并不一致,更增加了模型參數調優的困難。傳統參數調優時,需要高度依賴建模人員經驗,對參數進行不斷的調整優化,才能獲得較優性能,整個過程非常費時費力,且需要較高的專業領域知識。因此,如何實現自動化的超參數優化是機器學習中研究的重點。

1.2 模型超參數優化問題分析

為機器學習算法選擇較好的超參數是機器學習領域的一項重要研究課題,研究自動模型超參數優化方法,對于解放建模人員、快速尋找性能較好的模型超參數組合,提升模型參數調優的效率等具有重大的意義。自動超參數優化的方法主要有網格搜索、隨機搜索、貝葉斯優化、種群智能類方法等。(1) 網格搜索方法[3]對參數區間進行網格化,并通過遍歷網格參數的所有可能組合,來獲得最優結果,以提高機器學習最優參數的搜索效率。網格搜索法通過改變步長來提高參數搜索效率,參數的范圍和設置的步長會影響模型參數調優的速度,而且需要遍歷所有可能的組合,所以網格搜索法只能在參數較少且取值范圍較窄的模型中應用,在大規模的參數空間下性能往往表現很差。(2) 隨機搜索方法[4]和網格搜索類似,也需要在參數空間對參數進行搜索,但是搜索樣本點的選取服從概率分布,隨機搜索可以通過固定數量的搜索尋找到近似最優參數組合,得到的結果比網格搜索更好。但是隨機搜索沒有利用先前表現良好的區域,缺乏先驗經驗的使用造成存在大量不必要的評估,且不能保證尋找到的是最佳參數組合。(3) 貝葉斯優化方法[5-6]以高斯回歸模型作為代理模型,用先驗經驗與樣本信息進行綜合,不斷更新代理模型并產生新的采樣點,通過多次迭代從而產生最優超參數組合。貝葉斯搜索方法也可用來提升參數調優效率,但是貝葉斯搜索方法需要根據實際問題,結合相關領域知識選擇合適的代理函數與采集函數,而不同機器學習模型的參數是多樣的,很難找到一個全局的代理函數來近似。(4) 種群智能類方法,創建預定超參數的多個機器學習模型,通過模擬種群行為尋找最優變化趨勢,并據此調整搜索行為,從而找到最優超參數組合。實踐證明機器學習模型與種群智能方法相結合的超參數優化方法具有較好的應用效果。基于此,本文對粒子群優化算法進行改進,提出一種基于粒子群優化算法的模型超參數調優方法。

2 基于粒子群優化算法超參數調優方法

2.1 粒子群優化算法

粒子群優化算法[7](Particle Swarm Optimization,PSO)是Kennedy等提出的一種基于群體智能的優化方法。算法模擬了鳥類覓食的行為,由于鳥類在尋找食物時的有效策略是按照最近的飛行路徑進行搜索,算法模擬了該行為。PSO中每個粒子都代表優化問題的一個可能解,通過搜索每個粒子的最優解,并和粒子群整體共享,從而達到優化的目的。Shi等[8]對原始PSO進行優化,在速度更新公式中引入了慣性權重(w),慣性權重表明了對前一步粒子速度的繼承程度,含慣性權重的PSO稱為標準粒子群優化算法(SPSO)。SPSO的速度迭代公式可由式(1)表示。

(1)

2.2 慣性系數自適應調整策略

研究表明,隨著進化過程深入,慣性系數設置為遞減有助于算法優化性能的提高,取值范圍一般認為在0.4～0.9[9-10]。為使慣性系數能夠隨著搜索進程進行動態遞減,本文提出一種新的慣性系數更新的方法,具體為：更新的慣性系數=前若干輪迭代的慣性系數的均值×剩余迭代輪次+(模型參數組合中參數總數-本輪次更新的參數個數)/模型參數組合中參數總數,數學表達方式如式(2)所示。

(2)

改進后的慣性系數能夠跟隨算法的迭代運行而動態調整,擴大了算法的搜索空間,在初期能夠對全局進行充分探測,并在后期能夠針對可能有最優解的區域進行重點搜索。因而本文的粒子群算法在進行迭代過程中,每個粒子都能夠進行動態迭代更新,動態更新的慣性系數使得粒子尋優方法在性能上有所提高,針對不同的規模的數據都具有調整全局和局部的搜索能力。

3 基于粒子群優化算法超參數調優過程

3.1 機器學習模型超參數調優問題定義

基于粒子群優化算法的參數尋優過程可歸納成對一個數學優化問題的求解過程,該問題定義如下：設α1,α2,…,αn為機器學習模型的n個超參數,ek為機器學習訓練模型的損失函數,則基于粒子群優化算法的參數尋優問題定義如式(3)所示,約束條件如式(4)所示。

minek=F(α1,α2,…,αn)

(3)

s.t.αi∈[αimin,αimax]

(4)

式中：αimin、αimax為第i個超參數數值的最小值和最大值,即超參數αi的變化范圍。通過更新慣性系數和偏移量來動態更新粒子的速度和位置得到新的參數組合。當滿足基于訓練數據下的損失函數最小或達到設定訓練次數上限時,算法終止,并返回最優參數作為機器學習模型的超參數。

3.2 改進的模型超參數調優過程

基于粒子群優化算法的參數尋優過程如圖2所示。

圖2 基于粒子群優化算法的參數尋優過程

3.2.1設定超參數初始值和初始粒子群

確定粒子群算法超參數的初始值,包括偏移量、慣性系數、個體學習因子和群體學習因子。并確定機器學習模型的模型參數組合,隨機選出若干組模型參數組合訓練模型生成模型初始粒子群。

3.2.2迭代尋優,更新模型超參數組合

在整個迭代過程中,主要是通過更新粒子群算法中的慣性系數以及偏移量這兩個超參數,來更新粒子群中的模型參數組合。具體地,在每一輪迭代開始時,利用偏移量更新粒子群中的模型參數組合,每一次迭代結束更新慣性系數,并基于更新的慣性系數計算下一次迭代過程的偏移量。

1) 參數組合更新。在迭代過程中,新模型參數組合的具體方式如式(5)所示。

[α1,k,α2,k,…,αn,k]=[α1,k-1,α2,k-1,…,αn,k-1]+

[p1,k,p2,k,…,pn,k]

(5)

式中：[α1,k,α2,k,…,αn,k]為第k輪迭代的模型參數組合;[α1,k-1,α2,k-1,…,αn,k-1]為第k-1輪迭代的模型參數組合;[p1,k,p2,k,…,pn,k]為第k輪迭代的偏移量;下標n表示模型參數組合中的參數總數,k=1,2,…,K,K為最大迭代輪次,當k=1時,[α1,k-1,α2,k-1,…,αn,k-1]為模型初始粒子群中的模型參數組合。

2) 慣性系數更新。在迭代過程中,慣性系數的更新方式詳見2.2節,數學表達式參見式(2)。

3) 偏移量更新。在迭代過程中,下一次迭代過程的偏移量依據更新的慣性系數確定,如式(6)所示：

[p1,K+1,p2,K+1,…,pn,K+1]=GK+1·[p1,K,p2,K,…,pn,K]+

γg·[xg1,k,xg2,k,…,xgn,k]+

γq·[xq1,k,xq2,k,…,xqn,k]

k=1,2,…,K-1

(6)

式中：[p1,K,p2,K,…,pn,K]為第k輪迭代使用的偏移量;[p1,K+1,p2,K+1,…,pn,K+1]為更新的用于第k+1輪迭代使用的偏移量;Gk+1為更新的第k+1輪迭代使用的慣性系數;K為最大迭代輪次,下標n表示模型參數組合中的參數總數;γg為個體學習因子;γq為群體學習因子;[xg1,k,xg2,k,…,xgn,k]為第k輪迭代后當前個體與個體序列中最優解的差;[xq1,k,xq2,k,…,xqn,k]為第k輪迭代后當前個體與群體序列中最優解的差。

3.2.3算法參數限制和終止條件

模型參數組合中的每個參數設置一個最大偏移量,在迭代過程中更新偏移量時,每個參數的偏移量不超過其對應的最大偏移量。

在迭代過程中更新偏移量時,當參數的偏移量超過其對應的最大偏移量時,將該參數的偏移量賦值為最大偏移量。

當參數尋優迭代過程達到全局最優條件或者最大迭代輪次,結束迭代,并將得到的參數作為最優超參數組合返回給機器學習模型。

4 實證分析

4.1 應用場景說明

金融行業是數據高度密集型行業,數據不僅總量大,而且增長迅速。在金融行業企業數字化、智能化轉型過程中,機器學習算法模型發揮著無可替代的作用。因此探索自動化的機器學習超參數調優方法,將有助于金融行業企業深挖數據價值、提升機器學習模型性能,并有助于建立自動化的智能決策全流程,提升智能決策水平,豐富客戶體驗。

本文立足于提升模型超參數優化效果,在風控、營銷、推薦、催收、合規、消保等信用卡核心業務領域的模型中應用驗證,效果提升明顯。以下選取信用卡貸前審批和貸后催收兩個場景詳細介紹。其中信用卡貸前審批場景是信用卡企業綜合運用客戶各方面數據,決定客戶是否準入以及如何授信的場景,往往直接決定著信用卡業務的客戶質量,對信用卡企業的風險和收入有著直接的影響。信用卡貸后催收場景是指當客戶逾期后,銀行方面綜合運用各方面數據決定客戶的催收方式,以實現逾期款項收回的最大化。

本文選取金融業務中最常用的Xgboost、lightGBM和邏輯回歸(Logistic Regression,LR)模型作為研究的對象,進行對比分析。

4.2 實驗環境與編程示例

本文所涉及的實驗環境信息如下：(1) CPU型號：Intel(R) Xeon(R) Gold 6152 CPU @ 2.10 GHz。(2) CPU核心數量：88。(3) 內存：1 TB。(4) 操作系統：Red Hat Enterprise Linux Server 7.9(Maipo)。(5) 編程語言及主要框架：Python 3.8.4,Scikit-Learn 0.24,XGBoost 0.90.0,LightGBM 2.3.1,Matplotlib 3.5.3。

本文動態更新慣性系數和動態更新偏移量,核心偽代碼片段如下。

for i in range(max_iter)：

#迭代更新粒子移動速度

pop_velocity[i][index] =

weight*pop_velocity[i][index]+

c1*random.uniform(0,1)*(local_best[i][index]-pop[i][index])+c2*random.uniform(0,1)*(global_best[index]-pop[i][index])

#慣性權重線性遞減

if w_range：

weight-=w_range/max_iter

4.3 實驗結果

4.3.1信用卡貸前審批場景實驗效果

貸前風險模型基于客戶在準件前的相關數據,如客戶的征信信息、申請信息等,對客戶在未來的逾期概率做出預測。

分別選用Xgboost、lightGBM和LR模型進行訓練,訓練樣本共70萬條,初始特征2 000多個,每個模型在訓練時分別采用貝葉斯(BAYES)、粒子群優化(PSO)和網格(GRID)搜索算法進行超參數調優對比。三個模型進行參數調優的效果分別如圖3-圖5所示。

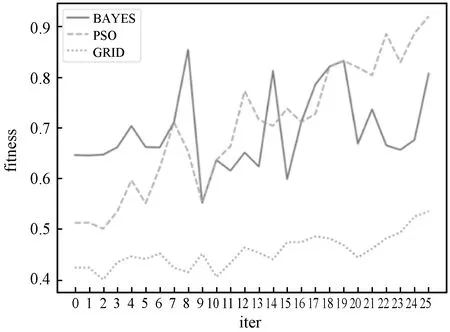
圖3 基于Xgboost貸前風險模型調優結果對比

圖4 基于lightGBM貸前風險模型調優結果對比

通過對比,可以看到在Xgboost、lightGBM和LR三種模型下,粒子群優化算法的調優效果都優于貝葉斯和網格搜索算法,且基于XGBOOST貸前風險模型得出效果較好,最終得到的最優參數如表1所示。

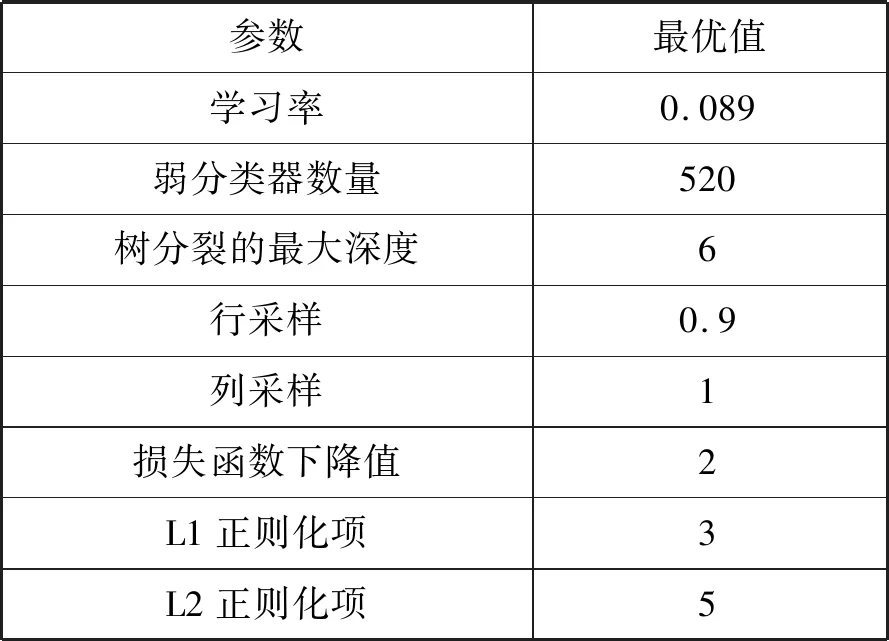
表1 貸前風險模型最終最優參數設置

4.3.2信用卡貸后催收場景實驗效果

貸后催收模型用來預判客戶最優的催收方式,應用于對逾期客戶制定差異化的催收分案策略。同貸前審批場景一樣,分別選用Xgboost、lightGBM和LR模型進行訓練,訓練樣本共17萬條,初始特征57個,每個模型在訓練時分別采用貝葉斯、優化后的粒子群搜索算法和網格搜索算法進行超參數調優對比。三個模型進行參數調優的效果分別如圖6-圖8所示。

圖6 基于Xgboost貸后催收模型調優結果對比

圖7 基于lightGBM貸后催收模型調優結果對比

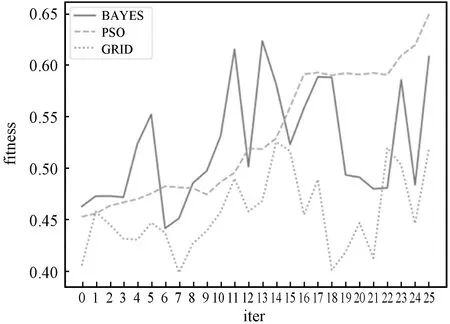
圖8 基于邏輯回歸算法貸后催收模型調優結果對比

通過對比,可以看到在貸后催收場景中,Xgboost、lightGBM和LR三種模型中,粒子群搜索算法的調優效果都優于貝葉斯和網格搜索算法,且基于XGBOOST貸后催收模型得出效果較好,最終得到的最優參數如表2所示。

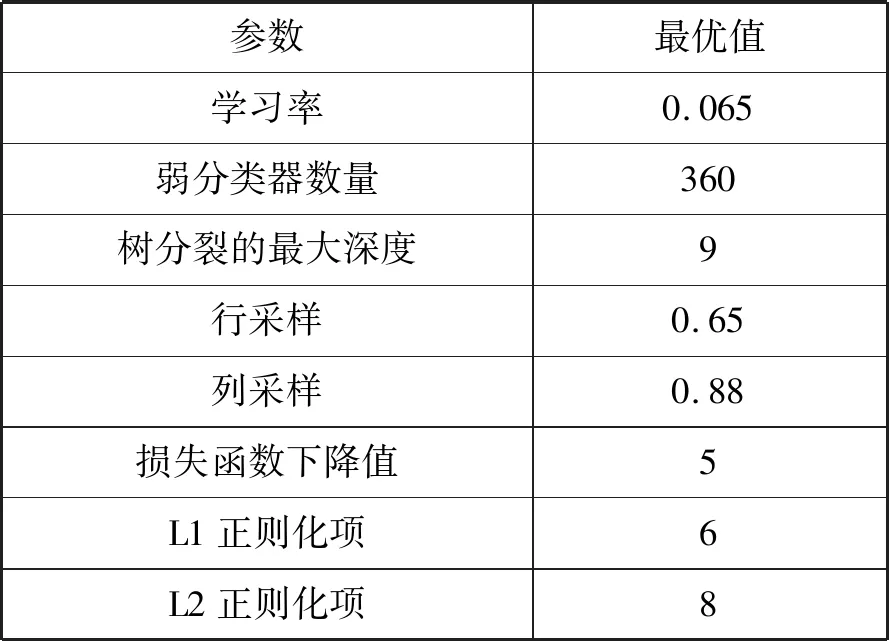
表2 貸后催收模型最終最優參數設置

4.3.3實驗結論

實驗數據表明,在信用卡業務常用的XGboost、lightGBM和LR三種模型中,本文提出的基于粒子群優化算法的模型超參數優化方法均優于貝葉斯算法和網格搜索的調優效果。貝葉斯算法在迭代尋優的過程中,波動性較大且隨著迭代輪次的加大,適應度與粒子群算法差距進一步拉大;而網格搜索算法,在預定的中止條件下無法得到相對于預期較理想的效果。相比之下,本文改進的粒子群算法能夠較好地提升模型的準確度,使得模型具有更高的預測精度和泛化能力。

5 結 語

本文基于標準粒子群優化算法,提出對其中慣性系數的設置方式進行優化,使之能夠隨著迭代處理過程進行動態調整,從而提高粒子群尋優方法的性能。通過在不同場景、不同模型中進行實驗對比,優化后的粒子群優化算法相對于貝葉斯算法、網格搜索算法都有著更優的調優能力,更適合在金融業務場景中應用。雖然粒子群超參數調優方法在金融數據中取得了較好的性能,但基于種群式的搜索成本是比較高的,無法直接適用于需要快速實現智能決策應用的場景。隨著金融科技的持續推進,越來越多的優秀算法被引入金融行業,從而不斷提升機器學習模型的應用成效。