關聯代數上零點可導映射的刻畫

莫增崇

(吉林師范大學 數學與計算機學院,吉林 四平 130000)

0 引言

關于代數在零點處的可導映射的研究一直是諸多學者關注的焦點[1-6]。朱軍[7]證明了有限CSL代數在零點處的范數連續的廣義可導映射是廣義導子。文獻[8]證明了δ是零點可導映射當且僅當有一個導子τ:T→T使得δ(A)=τ(A)+δ(I)A。李紅霞和段櫻桃[9]研究了標準算子代數上在零點處的可導映射與可導映射之間的關系,并得出了在零點處的可導映射是廣義內導子。文獻[10]證明了上三角矩陣代數上的零點Jordan可導映射是導子。近年來,對于關聯代數上映射的研究也引起了諸多學者的關注[11-14]。肖占魁[15]利用代數組合的方法刻畫了關聯代數上Jodan導子,并證明了關聯代數上的每一個Jordan導子是導子。張弦[16]證明了關聯代數上的Lie導子都是標準的。隨后文獻[17]把以上兩個文獻的結論推廣到Lie三重導子上。受以上研究的啟發,本文利用代數組合的方法刻畫了關聯代數上的零點可導映射。

1 預備知識

定義1設A是一個結合代數,φ:A→A是一個線性映射,如果對任意a,b∈A且ab=0,有φ(ab)=φ(a)b+aφ(b),則稱φ是零點可導映射。

定義2設A是一個結合代數,φ:A→A是一個線性映射,如果對任意a,b∈A且ab=0,有φ(ab+ba)=φ(a)b+aφ(b)+φ(b)a+bφ(a),則稱φ是零點Jordan可導映射。

定義3設R是含單位元的交換環,(X,≤)是一個局部有限的預序集,在R上定義關于X的關聯代數I(X,R):

I(X,R)

={f:X×X→R|f(x,y)=0,若x≤y不成立}

代數運算如下:

(f+g)(x,y)=f(x,y)+g(x,y)

(rf)(x,y)=rf(x,y)

?f,g∈I(X,R),r∈R,x,y,z∈X。其中乘積fg稱為卷積。

關聯代數I(X,R)的單位元定義為δ(x,y)=δxy,x≤y,其中δxy∈{0,1}是Kronecker符號。對于任意的x,y∈X滿足x≤y,定義基元exy(u,v)=1,若(u,v)=(x,y),其他情形為零。由卷積的定義可知exyeuv=δyuexv,關聯代數上的一組線性基記為B:{exy|x≤y}。

定義4設偏序集X中的序列為x=x0,x1,x2,…,xn=y,則對于任意的i=0,1,…,n-1滿足xi≤xi+1或xi≥xi+1,則在偏序集X中的元素x,y是連通的。

2 主要定理及證明

引理1[16]假設φ:I(X,R)→I(X,R)是一個R-線性映射,對任意i,j∈X且i≤j,記

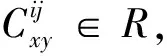
下面利用代數組合的方法給出了關聯代數上的零點可導映射的表達形式和滿足的系數關系式。

定理1設X是有限連通的預序集,φ是關聯代數I(X,R)上的零點可導映射,則

(1)

(2)

證明由零點可導映射的定義以及卷積的定義,對eii,eyy∈I(X,R),若y≠i,有eiieyy=δiyeiy=0,則

0=φ(eiieyy)=φ(eii)eyy+eiiφ(eyy)

(3)

(4)

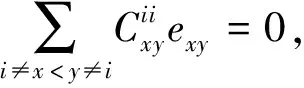
(5)

綜合(4)(5)可得

故(1)式得證。

由等式(1)知

對eii,eij∈I(X,R),有eijeii=δjieii=0,結合等式(1)則

0=φ(eijeii)=φ(eij)eii+eijφ(eii)

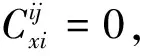
(6)

對ejj,eij∈I(X,R),有ejjeij=δjiejj=0,則

0=φ(ejjeij)=φ(ejj)eij+ejjφ(eij)

(7)

對eii,eij∈I(X,R),有eijeii=eiieijeii=0,則

0=φ(eijeii)=φ(eiieijeii)

=eiiφ(eij)eii+eijφ(eii)

(8)

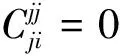
(9)

類似地,對exx,eij∈I(X,R),若x≠i,j,有exxeij=exxeijexx=0,則

0=φ(exxeij)=φ(exxeijexx)

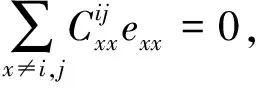
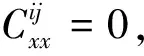
(10)

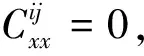
(11)

綜合(6)(7)(11)可得

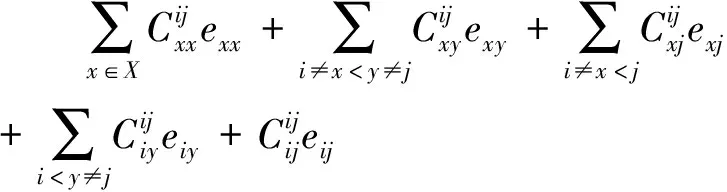
故(2)式得證。

(12)

(13)

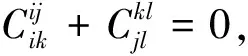
(14)

證明對任意的i≤j,k≤l,有eijekl=δjkeil,由零點可導映射的定義以及卷積定義,下面分三種情形討論。

情形1若i=j且k=l

情形1.1當i≠k時,有eiiekk=δikeik=0,結合等式(1)則

0=φ(eiiekk)=φ(eii)ekk+eiiφ(ekk)

當i=k時,由于eiiekk=δikeik≠0,不是零點,故不滿足。

情形2若i=j且k≠l(與若i≠j且k=l的情形對稱)

情形2.1當i≠k時,有eiiekl=δikeil=0,結合等式(1)(2)則

0=φ(eiiekl)=φ(eii)ekl+eiiφ(ekl)

當i=k時,由于eilekl=δikeil≠0,不是零點,故不滿足。

情形3若i≠j且k≠l

情形3.1當j≠k時,有eijekl=δjkeil=0,結合等式(2)則

0=φ(eijekl)=φ(eij)ekl+eijφ(ekl)

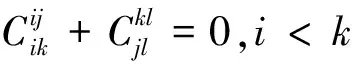
當j=k時,有eijekl≠0,不是零點,故不滿足。證畢。

引理2[16]假設φ:I(X,R)→I(X,R)是一個R-線性映射,對任意i,j∈X且i≤j,記

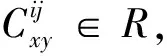
下面利用代數組合的方法給出了關聯代數上的零點Jordan可導映射的表達形式和滿足的系數關系式。

定理3設X是有限連通的預序集,φ是關聯代數I(X,R)上的零點Jordan可導映射,則

(15)

(16)

證明由零點Jordan可導映射的定義以及卷積的定義,對eii,exx∈I(X,R),若x≠i,有eiiexx=δixeix=0,則

0=φ(eiiexx+exxeii)

=φ(eii)exx+eiiφ(exx)+φ(exx)eii

+exxφ(eii)

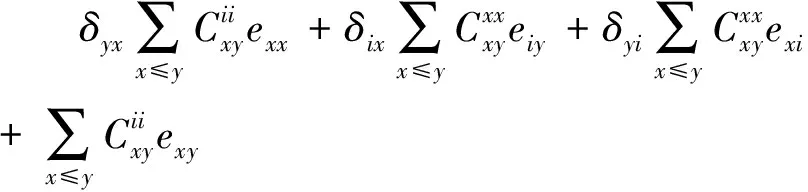
(17)

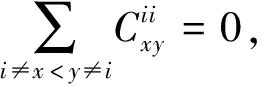
(18)

綜合(17)(18)可得

故(15)式得證。

對eij,eii∈I(X,R),有eijeii=δjieii=0,結合等式(15)則

φ(eij)=φ(eijeii+eiieij)

=φ(eij)eii+eijφ(eii)+φ(eii)eij

+eiiφ(eij)

(19)

對ejj,eij∈I(X,R),有ejjeij=δjiejj=0,結合等式(15)則

φ(eij)=φ(ejjeij+eijejj)

=φ(ejj)eij+ejjφ(eij)+φ(eij)ejj

+eijφ(ejj)

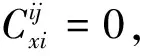
(20)

對于exx,eij∈I(X,R),當x≠i,j,有exxeij=exxeijexx=0,則

0=φ(exxeijexx+exxeijexx)

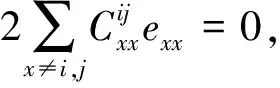
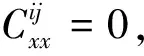
(21)

類似地,對eii,eij∈I(X,R),有eiieij=eiieijeii=0,則

0=φ(eiieijeii+eiieijeii)

=2eiiφ(eij)eii+2eijφ(eii)

(22)

類似地,對ejj,eij∈I(X,R),有ejjeij=ejjeijejj=0,則

0=φ(ejjeijejj+ejjeijejj)

=2φ(ejj)eij+2ejjφ(eij)ejj

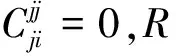
(23)

結合(21)(22)(23)可得

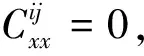
(24)

綜合等式(19)(20)(24)可得

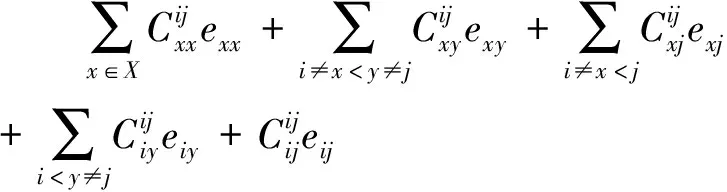
故(16)式得證。

(25)

(26)

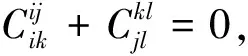
(27)

證明對任意的i≤j,k≤l,有eijekl+ekleij=δjkeil+δliekj,由零點Jordan可導映射的定義以及卷積定義,下面分三種情形討論。

情形1若i=j且k=l

情形1.1當i≠k時,對eii,ekk∈I(X,R),有eiiekk=δikeik=0,則

0=φ(eiiekk+ekkeii)

=φ(eii)ekk+eiiφ(ekk)

+φ(ekk)eii+ekkφ(eii)

當i=k時,eiiekk=δikeik≠0,不是零點,故不滿足。

情形2若i=j且k≠l(與若i≠j且k=l的情形對稱)

情形2.1當i≠k和i≠l時,對eii,ekl∈I(X,R),有eiiekl=δikeil=0,則

0=φ(eiiekl+ekleii)

=φ(eii)ekl+eiiφ(ekl)

+φ(ekl)eii+eklφ(eii)

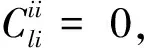
情形2.2當i≠k和i=l時,對eii,ekl∈I(X,R),有eiiekl=δikeil=0,則

φ(eki)=φ(eiieki+ekieii)

=φ(eii)ekl+eiiφ(eki)

+φ(eii)eki+eiiφ(eki)

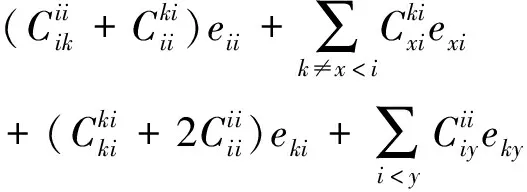
當i=k和i=l時以及i=k和i≠l時,不是零點,都不滿足。

情形3若i≠j且k≠l

情形3.1當j≠k且l≠i,對eij,ekl∈I(X,R),有eijekl=δjkeil=0,則

0=φ(eijekl+ekleij)

=φ(eij)ekl+eijφ(ekl)

+φ(ekl)eij+eklφ(eij)

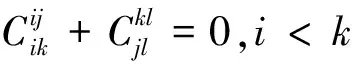
情形3.2當j≠k和l=i時,對eij,ekl∈I(X,R),有eijeki=δjkeii=0,則

φ(ekj)=φ(eijeki+ekieij)

=φ(eij)eki+eijφ(eki)

+φ(eki)eij+ekiφ(eij)

當j=k和l≠i以及j=k和l=i時,不是零點,都不滿足,證畢。

定理5設X是有限連通的預序集,R是含有單位元的2-扭自由的交換環,則關聯代數I(X,R)上的每一個零點Jordan可導映射是零點可導映射。

證明設φ:I(X,R)→I(X,R)是零點可導映射,由定理1和定理2可得

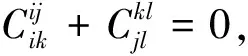
在R上定義線性映射φ

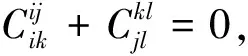
由定理3和定理4可知φ是零點Jordan可導映射且線性映射:θ=φ-φ滿足

θ(eii)=φ(eii)-φ(eii)=0

θ(eij)=φ(eij)-φ(eij)=0

故得證。