基于TypeB 卡閱讀器的數(shù)字解調(diào)算法

陳俊凝

（西北大學(xué) 信息科學(xué)與技術(shù)學(xué)院，西安 710127）

非接觸式IC 卡系統(tǒng)由鄰近卡（PICC）和近耦合設(shè)備（PCD）組成[1]，兩者通過無線通信來完成信息傳輸。然而，PCD 解調(diào)誤差大、速度慢，將出現(xiàn)系統(tǒng)無法正確通信的問題。解調(diào)能力提升，不僅可以發(fā)揮PICC 芯片性能優(yōu)勢(shì)，還能夠提升自身的可靠性和安全性，這對(duì)系統(tǒng)的運(yùn)行起到關(guān)鍵性作用[2]。

對(duì)于符合ISO/IEC 14443[3]TypeB 標(biāo)準(zhǔn)的PICC，其發(fā)送給PCD 的數(shù)字信息也是被附加在847 kHz 的副載波上的，再利用負(fù)載調(diào)制將雙重載波發(fā)送給PCD，波特率為106 kbps。簡而言之，就是通過106 kbps 的數(shù)字信號(hào)對(duì)847 kHz 的副載波信號(hào)進(jìn)行二進(jìn)制相移鍵控（BPSK）調(diào)制，根據(jù)協(xié)議規(guī)定，采用連續(xù)8 個(gè)周期初始相位固定的副載波信號(hào)來表示“0”，“1”則用與初始相位相差為連續(xù)8 個(gè)周期的副載波信號(hào)表示[4]。

1 BPSK 相干解調(diào)關(guān)鍵技術(shù)

BPSK 調(diào)制利用載波信號(hào)的相位信息調(diào)制，包絡(luò)檢波無法檢測(cè)到相位變化，因此采用相干解調(diào)方式更為理想[5]。特別是在PICC 和PCD 進(jìn)行信息交互時(shí)，由于信號(hào)較弱，再加上外界干擾，信號(hào)在傳送過程中很容易產(chǎn)生偏差，導(dǎo)致本地振蕩產(chǎn)生的相干載波不能嚴(yán)格實(shí)現(xiàn)同頻同相，并且大大影響了解調(diào)性能，因此在接收端實(shí)現(xiàn)載波同步非常重要[6]。

本文對(duì)傳統(tǒng)解調(diào)算法進(jìn)行了深入研究，結(jié)合實(shí)際工程的需要，針對(duì)BPSK 相干解調(diào)過程中的載波同步、碼元同步等關(guān)鍵技術(shù)進(jìn)行研究與實(shí)現(xiàn)，并且提出了優(yōu)化方案加以對(duì)比分析。

2 載波同步

2.1 傳統(tǒng)Costas 環(huán)路原理

鎖相環(huán)在調(diào)制解調(diào)中發(fā)揮著重要作用[7]，其是一種典型的反饋控制電路，能夠鎖定相位[8]。

然而傳統(tǒng)鎖相環(huán)技術(shù)對(duì)本地時(shí)鐘頻率要求較高，在跟蹤載波時(shí)無法有效糾正較大頻偏，也不適合寬率范圍內(nèi)的基帶碼元同步。

Costas 環(huán)[9]基于鎖相環(huán)原理，其原理框圖如圖1所示。

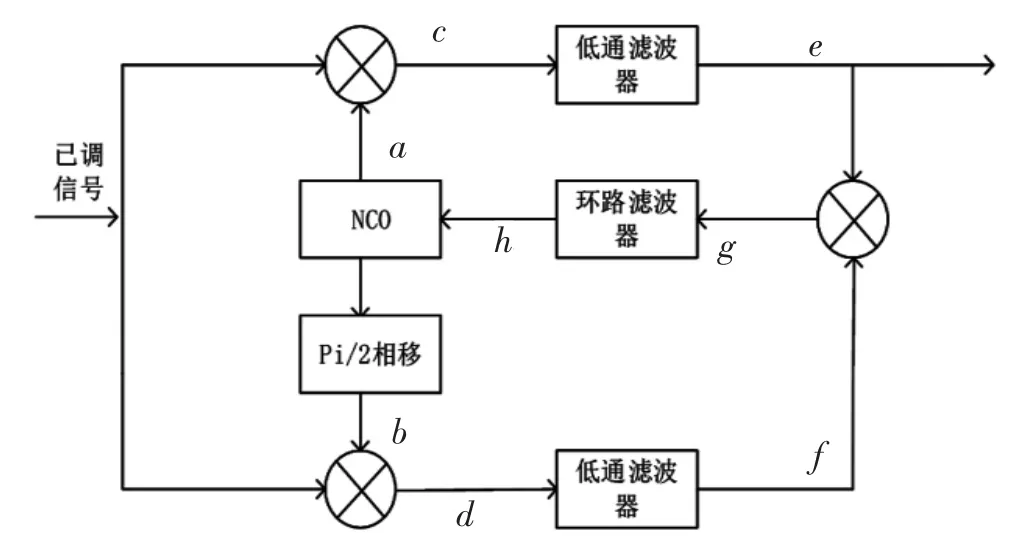
圖1 Costas 同步環(huán)路原理框圖

BPSK 信號(hào)被送入兩路相乘器，與壓控振蕩器產(chǎn)生的a、b 兩點(diǎn)電壓相乘，得到c、d 兩點(diǎn)電壓，分別經(jīng)過低通濾波器后相乘得到環(huán)路濾波器的輸入電壓vg為

式中：m（t）為調(diào)制信號(hào)，φ-θ 為本地信號(hào)與載波信號(hào)的相位差。對(duì)于BPSK 信號(hào)而言，m（t）=±1，并且在φ-θ 很小時(shí)，sin（φ-θ）=φ-θ，那么式（1）便可改寫為

這時(shí)vg通過環(huán)路濾波器間接控制數(shù)控振蕩器的頻率，環(huán)路濾波器的作用就是低通，僅允許vg中的直流分量通過，數(shù)控振蕩器（NCO）受到電壓控制后調(diào)整頻率不斷使φ-θ 盡可能變小，直到它減小為0 時(shí)，就可以得到vg=1/2m（t）。

此時(shí)的電壓和需要解調(diào)出的信號(hào)m（t）只是幅值不同，直接輸出這個(gè)電壓就可以得到近似的解調(diào)結(jié)果。

2.2 基于希爾伯特鑒相的解調(diào)算法原理

傳統(tǒng)的Costas[10]環(huán)解調(diào)效果較為理想，不過其仍然存在某些缺點(diǎn)，載波頻率高的時(shí)候，對(duì)濾波器特性要求也就變高，因此在實(shí)際應(yīng)用中，常搭配叉積鑒頻算法[11]來提高效率，實(shí)現(xiàn)起來會(huì)有些繁瑣。本文在Costas 環(huán)法上做了部分改進(jìn)，改進(jìn)的結(jié)構(gòu)如圖2 所示。

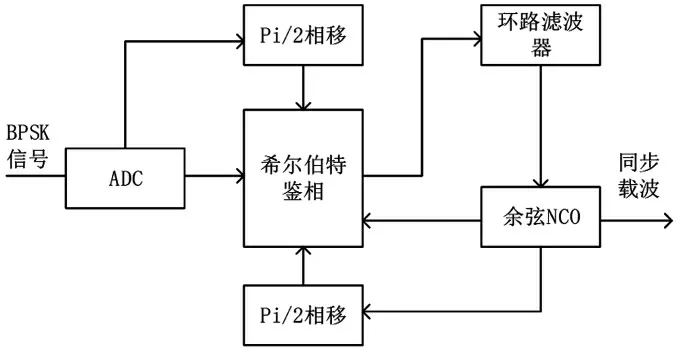
圖2 基于希爾伯特鑒相的解調(diào)原理框圖

希爾伯特鑒相模塊總共有四路輸入信號(hào)，與模數(shù)轉(zhuǎn)換器（ADC）采樣后的已調(diào)波和控制余弦NCO 產(chǎn)生的的信號(hào)有關(guān)，其中已調(diào)信號(hào)與其90°相移的信號(hào)固定不變，NCO 經(jīng)過環(huán)路不斷調(diào)整生成的余弦波和90°相移后的正弦波持續(xù)進(jìn)入鑒相模塊，這些信號(hào)在模塊內(nèi)部按照算法進(jìn)行數(shù)學(xué)運(yùn)算，得到相位差。計(jì)算過程如下。

設(shè)m為接收端收到的BPSK 調(diào)制信號(hào)，mh是調(diào)制信號(hào)移相90°后的信號(hào)，α 是余弦NCO 信號(hào)，β 是α 經(jīng)過90°相移的信號(hào)，ωc是載波中心頻率，△ω 為頻偏，θ是載波的相位差，即

因此可以得到

運(yùn)算結(jié)果便是本地載波與調(diào)制信號(hào)的相位差。

3 位同步

Gardner 算法[12]利用反饋環(huán)路，使得這種算法收斂速率高，運(yùn)算量更小，所以本文選用了Gardner 定時(shí)同步環(huán)路實(shí)現(xiàn)碼元同步，其原理框圖如圖3 所示。

圖3 Gardner 算法原理框圖

傳統(tǒng)Gardner 定時(shí)環(huán)路通常在每個(gè)碼元內(nèi)的采樣點(diǎn)數(shù)較少，不能根據(jù)初始賦值來直接鎖定最佳抽樣時(shí)刻，必須通過內(nèi)插濾波器和NCO 模塊不斷地反饋計(jì)算出最佳采樣點(diǎn)。對(duì)于本文所設(shè)置的參數(shù)，采樣頻率明顯超過了碼元速率，可以在每個(gè)碼元內(nèi)取得31 個(gè)采樣點(diǎn)，在這些采樣點(diǎn)中，有位于最佳采樣時(shí)刻附近的值。

4 硬件實(shí)現(xiàn)

4.1 載波同步的硬件實(shí)現(xiàn)

載波同步模塊采用Costas 同步環(huán)路由環(huán)路濾波器、NCO 以及希爾伯特鑒相器等構(gòu)成。

對(duì)于環(huán)路濾波器，為了節(jié)省系統(tǒng)的硬件邏輯資源，簡化計(jì)算，在不影響系統(tǒng)正常運(yùn)行、確保誤差在允許范圍內(nèi)，對(duì)環(huán)路系數(shù)的小數(shù)部分進(jìn)行數(shù)據(jù)處理，將其轉(zhuǎn)換為近似相等與2 的負(fù)整數(shù)次冪的值，這樣就可以直接采用右移法對(duì)環(huán)路進(jìn)行運(yùn)算。

NCO 模塊主要功能是產(chǎn)生同相的相干載波，然后通過低通濾波器得到數(shù)字基帶信號(hào)，可以利用直接數(shù)字式頻率合成器（DDS）原理實(shí)現(xiàn)NCO 功能。在設(shè)計(jì)時(shí)，為了減少ROM 占用的硬件資源，只在ROM 中存儲(chǔ)1/4 周期的余弦波對(duì)應(yīng)的值，其他周期的的值通過算法來計(jì)算。

希爾伯特鑒相器由4 個(gè)乘法器、2 個(gè)加法器以及1個(gè)實(shí)現(xiàn)反三角函數(shù)運(yùn)算的CORDIC 算法模塊[13]組成，其結(jié)構(gòu)如圖4 所示。乘法器和加法器采用QuartusⅡ中的IP 核即可生成，CORDIC 算法模塊采用16 級(jí)流水線設(shè)計(jì)，將x0、y0和θ=0 導(dǎo)入到寄存器中，利用流水線對(duì)n 個(gè)固定的右移結(jié)構(gòu)實(shí)現(xiàn)n 次迭代，這種結(jié)構(gòu)盡管沒有將邏輯資源的利用率降低，但是采用了較為簡單的右移結(jié)構(gòu)，簡化了邏輯結(jié)構(gòu)，有效提升了系統(tǒng)的時(shí)鐘性能。此外，采用流水線結(jié)構(gòu)也可以提高算法的運(yùn)行速率，相比直接循環(huán)式結(jié)構(gòu)的實(shí)現(xiàn)方法，速率提高了n倍，是高速系統(tǒng)中的關(guān)鍵點(diǎn)。反三角函數(shù)對(duì)應(yīng)的值存放在ROM 中，可以減少資源占用空間。

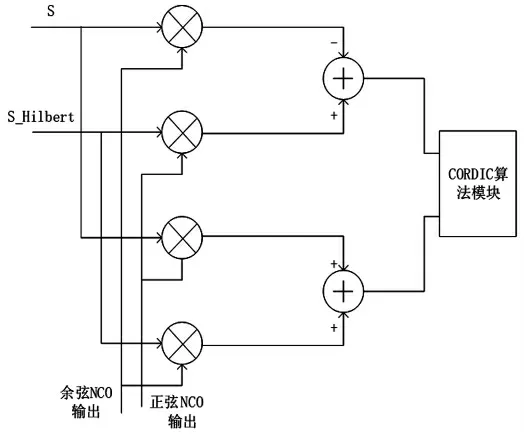
圖4 希爾伯特鑒相算法模塊

4.2 位同步的硬件實(shí)現(xiàn)

本文采用Gardner 定時(shí)同步環(huán)路實(shí)現(xiàn)位同步，由內(nèi)插濾波器、定時(shí)誤差檢測(cè)、環(huán)路濾波器以及NCO 模塊構(gòu)成。其中環(huán)路濾波器與NCO 模塊與內(nèi)插濾波器模塊使用Farrow 結(jié)構(gòu)，實(shí)現(xiàn)了基于拉格朗日多項(xiàng)式的立方插值濾波器功能[14]，該結(jié)構(gòu)的濾波器由FIR 濾波器實(shí)現(xiàn)，濾波器參數(shù)由仿真工具FDATOOL 得到。

4.3 硬件測(cè)試結(jié)果

硬件實(shí)現(xiàn)和模擬BPSK 通信搭建的現(xiàn)場(chǎng)可編程門陣列（FPGA）硬件仿真環(huán)境如圖5 所示。

圖5 BPSK 通信實(shí)物圖

為了得到與測(cè)試結(jié)果相比較的絕對(duì)基準(zhǔn)來評(píng)估解調(diào)效果，需要得到協(xié)議的誤碼率或丟包率的理論極限，推導(dǎo)出理論極限為

式（8）分別描述了1 bit 信號(hào)能量值Eb與有效電壓值VSrms和比特持續(xù)時(shí)間Tb、功率譜密度N0與噪聲有效電壓VNrms和噪聲帶寬BW 之間的關(guān)系；式（9）為BPSK 解調(diào)誤碼率計(jì)算公式；式（10）描述了數(shù)據(jù)丟包率和誤碼率的轉(zhuǎn)換關(guān)系。

將解調(diào)得到的數(shù)據(jù)導(dǎo)入Matlab 中進(jìn)行處理，得到數(shù)據(jù)在傳輸過程中的丟包率，將理論、實(shí)際以及原解調(diào)算法所得數(shù)據(jù)整合，得到丟包率（PER）對(duì)比結(jié)果，如圖6 所示。

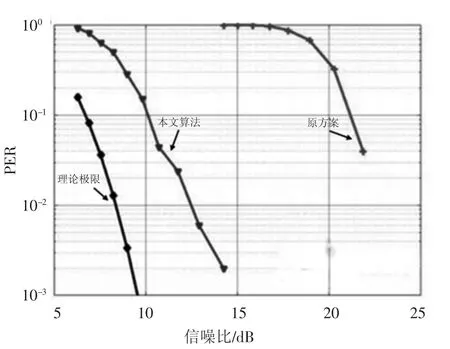
圖6 理論、實(shí)際及原算法丟包率對(duì)比

圖6 中由左至右曲線分別為理論極限、本文算法、原芯片解調(diào)方案在不同信噪比情況下的丟包率，每一個(gè)數(shù)據(jù)點(diǎn)發(fā)送500 個(gè)數(shù)據(jù)包。可以看到，在0.1 PER 值處，TypeB 的理論極限與實(shí)際測(cè)量結(jié)果存在3.1 dB 的差異，這是因?yàn)槔碚摌O限不包括數(shù)據(jù)包在開始或結(jié)束檢測(cè)時(shí)的錯(cuò)誤概率，只包含了誤碼率。可以看到在PER值為0.1 的情況下，相比原解調(diào)算法，本文設(shè)計(jì)算法所需信噪比環(huán)境降低了11 dB 左右，這說明本文設(shè)計(jì)算法可行，并且性能優(yōu)于原解調(diào)算法。

5 結(jié)論

本文提出基于希爾伯特變換的BPSK 解調(diào)算法并完成了算法的硬件實(shí)現(xiàn)，通過對(duì)該算法、某款PCD 芯片解調(diào)算法的仿真，比較其在不同噪聲環(huán)境下的丟包率得到該算法的解調(diào)優(yōu)勢(shì)：相比原算法，信噪比環(huán)境均降低了11 dB 左右，在低信噪比環(huán)境下，也能正確獲取數(shù)據(jù)，解調(diào)效果顯著提升。

因此，基于希爾伯特變換的BPSK 解調(diào)方案，合理可行且容易實(shí)現(xiàn)。有望在RFID 技術(shù)中得到廣泛應(yīng)用。