“一線三直角”全等模型的應用
孫衛華


在平面幾何中,有許多基本圖形,我們稱之為基本模型. 同學們解題時若能發現或構造基本模型,并靈活運用基本模型的有關性質來解決問題,往往會事半功倍.
模型解讀
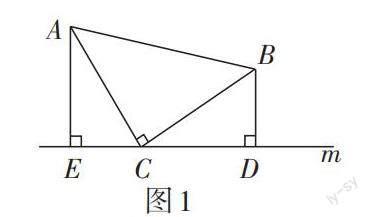
三個直角的頂點落在同一條直線上的圖形,被稱為“一線三直角”基本模型. 它的常見形式有兩種:一是兩直角三角形在直線的同側,如圖1(又稱“K”字型);二是兩直角三角形在直線的兩側,如圖2.
在圖1和圖2中,∠ACB = ∠AEC = ∠BDC = 90°,若AC = CB(或AE = CD或EC = DB),則△AEC ≌ △CDB.? 這兩個圖形分別在人教版教材第52頁和第56頁出現過.
在較復雜的圖形中,若能尋找或構造出“一線三直角”全等模型,則可迅速找到解決問題的路徑.
模型應用
變式1 將模型中的全等三角形的對應線段相等關系轉化為線段和差關系.
例1 如圖3,已知四邊形ABCD是正方形,G為線段AD上任意一點,CE⊥BG于點E,DF⊥CE于點F. 求證:DF = BE + EF.
解析:[∵]四邊形[ABCD]是正方形,[∴BC=CD],[∠BCD=90°],
[∴∠BCE+∠DCF=90°].
[∵]CE[⊥]BG,DF[⊥]CE,[∴∠BEC=∠CFD=90°],[∴∠BCE+∠CBE=90°],
[∴∠CBE=∠DCF],[∴△BCE≌△CDF(AAS)],[∴BE=CF,CE=DF],
[∴CE=CF+EF=BE+EF],[∴DF=BE+EF].
反思:由圖2迅速找到圖3中“一線三直角”全等模型是解題關鍵.
變式2 將模型中的全等三角形對應線段相等關系轉化為點坐標的確定.
例2 如圖4,在△ABC中,∠ACB = 90°,AC = BC,點C的坐標為(-2,0),點A的坐標為(-6,3),則點B的坐標是___________.
解析:過點A,B分別作AD⊥x軸于點D,BE⊥x軸于點E,則∠ADC = ∠ACB = ∠BEC = 90°. 由基本模型圖1可知圖4中△ADC≌△CEB,所以AD = CE,CD = BE. 又因為點C(-2,0),點A(-6,3),所以AD = 3,CD = 6 - 2 = 4,所以BE = 4,CE = 3,所以OE = 3 - 2 = 1,所以B的坐標為(1,4). 故應填(1,4).
反思:受基本模型圖1的啟發,添加輔助線,找到圖4中“一線三直角”全等模型是解題的關鍵.
變式3 將三個直角的頂點落在同一條直線上,并將部分直角隱去.
例3 如圖5,在四邊形ABCD中,∠B = 90°,AD[?]BC,△CDC′是等腰直角三角形,∠CDC′= 90°. 若AD = 2,△ADC′的面積等于3,求BC的長.
解析:盡管圖5中看上去沒有“一線三直角”模型,但受圖1的啟發,過點D作EF⊥BC于點E,過點C′作C′F⊥EF于點F,就出現了“一線三直角”模型,由上述模型可知△CDE≌△DC'F,所以CE = DF. 又因為AD = 2,△ADC′的面積等于3,所以DF = 3,所以CE = DF = 3,所以BC = BE + CE = 2 + 3 = 5.
反思:這里沒有“一線三直角”模型的影子,但受基本模型的啟發,可以“無中生有”地創新使用模型.
分層作業
難度系數:★★★解題時間:10分鐘
如圖6①所示,已知A,B為直線l上兩點,點C為直線l上方一動點,連接AC,BC,分別以AC,BC為邊向△ABC外作正方形CADF和正方形CBEG,過點D作DD1⊥l于點D1,過點E作EE1⊥l于點E1. (1)如圖6②,當點E恰好在直線l上時(此時E1與E重合),試說明DD1 = AB;(2)在圖6①中,當D,E兩點都在直線l的上方時,試探求三條線段DD1,EE1,AB之間的數量關系,并說明理由;(3)如圖6③,當點E在直線l的下方時,請寫出三條線段DD1,EE1,AB之間的數量關系,并說明你的理由. (答案見第37頁)
(作者單位:江蘇省泰州市姜堰區城西實驗學校)

