基于多項(xiàng)式混沌方法對(duì)C-J 爆轟參數(shù)不確定度的分析*

梁 霄，王瑞利，胡星志，陳江濤

（1. 山東科技大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，山東 青島 266590；2. 北京應(yīng)用物理與計(jì)算數(shù)學(xué)研究所，北京 100094；3. 中國(guó)空氣動(dòng)力研究與發(fā)展中心，四川 綿陽(yáng) 621000）

爆轟是極其劇烈的物理化學(xué)反應(yīng)，炸藥爆炸過(guò)程擴(kuò)展的速度高達(dá)每秒數(shù)千米到萬(wàn)米之間，所形成的溫度約為3 000～5 000 ℃，壓力高達(dá)102～104MPa，發(fā)生在極短的時(shí)間（10-9s 量級(jí)）和極窄的空間（10-4m量級(jí)），釋放極高的能量（102GW/cm2量級(jí)）[1-5]。爆轟過(guò)程的極端特征給試驗(yàn)精確測(cè)量和理論表征帶來(lái)了極大挑戰(zhàn)。由于爆轟試驗(yàn)成本高和化學(xué)反應(yīng)的不穩(wěn)定性，只有經(jīng)過(guò)多次試驗(yàn)才能標(biāo)定感興趣量（quantity of interest, QoI）的取值。即使是常規(guī)炸藥，也只有有限的試驗(yàn)數(shù)據(jù)。與試驗(yàn)相比，建模與模擬（modeling and simulation, M&S）是一種經(jīng)濟(jì)、安全的途徑。為降低運(yùn)算成本，提高計(jì)算可行性，通常還使用假設(shè)、簡(jiǎn)化和近似等手段，以降低模型的復(fù)雜性[1,4-6]。Chapman-Jouguet（C-J）理論假設(shè)流動(dòng)是一維的，不考慮熱傳導(dǎo)、熱輻射以及黏滯摩擦等耗散效應(yīng)，忽略沖擊起爆過(guò)渡和不定常效應(yīng)，將復(fù)雜非線性多物理爆轟過(guò)程簡(jiǎn)化為一個(gè)具有沖擊壓縮間斷面的一維問(wèn)題。C-J 理論能建立波后QoIs 和爆速、初始密度以及唯象參數(shù)的函數(shù)關(guān)系式，能預(yù)測(cè)爆壓和爆熱等不易測(cè)量或測(cè)量成本較高的物理量，具有實(shí)用性強(qiáng)、適用范圍廣的優(yōu)點(diǎn)，是高能炸藥爆轟研究的有效工具[5-6]。

C-J 理論是學(xué)術(shù)界公認(rèn)的成功理論，其模擬過(guò)程中使用的物理量和參數(shù)一直被認(rèn)為是確定的。事實(shí)上，由于炸藥組分的異質(zhì)性以及物理量測(cè)量的隨機(jī)特征，物理量和唯象參數(shù)都會(huì)受到不確定性的干擾。例如，爆速是描述炸藥力學(xué)行為的基本物理量，某些HMX 基高能炸藥的爆速超過(guò)9×103m/s，速度的瞬時(shí)極大變化率導(dǎo)致缺乏精密的試驗(yàn)裝置進(jìn)行測(cè)試。傳統(tǒng)的試驗(yàn)裝置如圓筒試驗(yàn)，所用金屬的純度和密度不均勻性、加工公差的存在以及試驗(yàn)數(shù)據(jù)的擬合誤差，都會(huì)導(dǎo)致測(cè)量結(jié)果的不確定性。同時(shí)，含能材料組分的細(xì)微變化、幾何邊界的不精確、極端荷載下金屬延展性變化以及黏結(jié)劑的存在也會(huì)導(dǎo)致試驗(yàn)結(jié)果的波動(dòng)[7-9]。

密度是決定爆轟性能的另一個(gè)基本物理量。密度的不確定度來(lái)自于炸藥加工過(guò)程中產(chǎn)生的空腔、孔隙、裂紋、扭結(jié)和顆粒結(jié)晶的隨機(jī)性以及雜質(zhì)的混入[10]。此外，存儲(chǔ)溫度的變化也會(huì)引起密度的波動(dòng)[11]。密度的微小變化會(huì)激發(fā)感度和熱點(diǎn)的變化，甚至?xí)鸨Z系統(tǒng)輸出結(jié)果劇烈的、奇異的甚至目前理論無(wú)法解釋的變動(dòng)[7,12]。

綜上所述，爆轟實(shí)際過(guò)程中，如爆速和初始密度等物理量都會(huì)受到噪聲擾動(dòng)。這類(lèi)不確定度是炸藥的固有屬性，即使增加樣本容量，也很難減少或降低這種不確定性。另一方面，爆轟產(chǎn)物狀態(tài)方程、反應(yīng)率函數(shù)等爆轟唯象模型中的參數(shù)，無(wú)法通過(guò)試驗(yàn)直接標(biāo)定，需要憑借工程技術(shù)人員的經(jīng)驗(yàn)[3,13-14]，這類(lèi)不確定性也會(huì)嚴(yán)重影響炸藥爆轟數(shù)值模擬的精度和可信性。

事實(shí)上，工程技術(shù)人員和學(xué)者們都已經(jīng)意識(shí)到爆轟中的不確定因素[1,5-6,9,15]。文獻(xiàn)[1, 6]甚至將物理量的容許不確定度（誤差）定為 ±5 %。然而，很少有學(xué)者專(zhuān)門(mén)研究不確定因素對(duì)QoI 的影響。實(shí)際上，不確定因素的存在使得研究人員一直面臨著試驗(yàn)成本太高和數(shù)值模擬不穩(wěn)定的矛盾心態(tài)。導(dǎo)致研究人員既想利用C-J 理論這種經(jīng)濟(jì)、安全的手段，又對(duì)C-J 理論的使用范圍和預(yù)測(cè)結(jié)果心存疑慮。因此，爆轟不確定度量化（uncertainty quantification, UQ）研究是增強(qiáng)炸藥爆轟唯象模型的可靠性、標(biāo)定模型的使用范圍、緩和試驗(yàn)與數(shù)值模擬矛盾的重要途徑，具有重要的學(xué)術(shù)意義和實(shí)用價(jià)值。

近10 年來(lái)，歐美UQ 技術(shù)在水文、地理、預(yù)報(bào)、經(jīng)濟(jì)、自動(dòng)控制和結(jié)構(gòu)力學(xué)分析等領(lǐng)域蓬勃發(fā)展。但爆轟UQ 研究結(jié)果較少，面臨眾多挑戰(zhàn)。首先，在刻畫(huà)炸藥爆轟模型中輸入不確定度方面，數(shù)理統(tǒng)計(jì)理論完備，技術(shù)成熟，是量化不確定度的最自然的工具。根據(jù)大數(shù)定律和中心極限定理，正態(tài)分布是描述輸入不確定度的有效工具，且參數(shù)易于通過(guò)經(jīng)典假設(shè)檢驗(yàn)法標(biāo)定。然而，正態(tài)分布無(wú)法保證密度和爆速的非負(fù)性。其次，在如何準(zhǔn)確得到炸藥產(chǎn)物狀態(tài)方程（equation of state, EOS）和反應(yīng)率函數(shù)等唯象模型中參數(shù)的可信取值范圍方面，通常根據(jù)工程技術(shù)人員的經(jīng)驗(yàn)給定取值范圍，存在很大的人為因素。若假設(shè)參數(shù)服從此區(qū)間上的、無(wú)信息的（un-informative）均勻分布，很多重要信息會(huì)丟失。獨(dú)立同分布是數(shù)理統(tǒng)計(jì)中的重要假設(shè)，但爆轟系統(tǒng)的輸入不確定度未必滿足此假設(shè)。除此之外，針對(duì)如何評(píng)估輸入不確定度對(duì)系統(tǒng)響應(yīng)量的影響方面，即使通過(guò)大規(guī)模工程計(jì)算，也很難給出QoIs 的概率密度函數(shù)（probability density function, PDF）的顯式函數(shù)關(guān)系。幸運(yùn)的是，計(jì)算技術(shù)的快速發(fā)展和數(shù)值分析方法的進(jìn)步提供了計(jì)算PDF 的有效方法。與Monte Carlo 方法相比，多項(xiàng)式混沌（polynomial chaos, PC）收斂速度快、運(yùn)算成本低，是目前工程技術(shù)領(lǐng)域處理不確定度傳播的主流工具[3,16-18]。特別是非嵌入式PC，不需要更改程序，且能給出Gauss 統(tǒng)計(jì)量的顯式表達(dá)，是處理爆轟UQ 的潛在工具。但是在爆轟UQ 研究中，會(huì)面臨輸入不確定度概率類(lèi)型不一致、隨機(jī)變量不獨(dú)立的問(wèn)題，導(dǎo)致PC 理論無(wú)法直接應(yīng)用。

面對(duì)眾多挑戰(zhàn)，本文中，結(jié)合真實(shí)的試驗(yàn)數(shù)據(jù)，通過(guò)參數(shù)估計(jì)和Anderson-Darling 假設(shè)檢驗(yàn)法標(biāo)定物理量的PDF，采用Beta 分布定量刻畫(huà)沒(méi)有物理意義的、唯象參數(shù)的不確定度，評(píng)估輸入不確定度對(duì)QoIs 的影響，以增強(qiáng)C-J 模型的可靠性和預(yù)測(cè)精度，以期為武器型號(hào)設(shè)計(jì)、裝甲防護(hù)和土木施工管理等提供決策依據(jù)。

1 Chapman-Jouguet 理論

假設(shè)爆轟波運(yùn)動(dòng)方向和波陣面垂直，忽略波陣面的厚度和化學(xué)反應(yīng)時(shí)間，忽略熱傳導(dǎo)和黏性效應(yīng)以及非定常效應(yīng)，則爆轟過(guò)程可簡(jiǎn)化為圖1 所示的C-J 模型。圖1 中，ρ0、p0、U0和e0分別代表未反應(yīng)物的初始密度、壓力、速度和內(nèi)能，D為爆速。爆炸物以D–U0的速度進(jìn)入波陣面，以D–U1的速度流出波陣面。

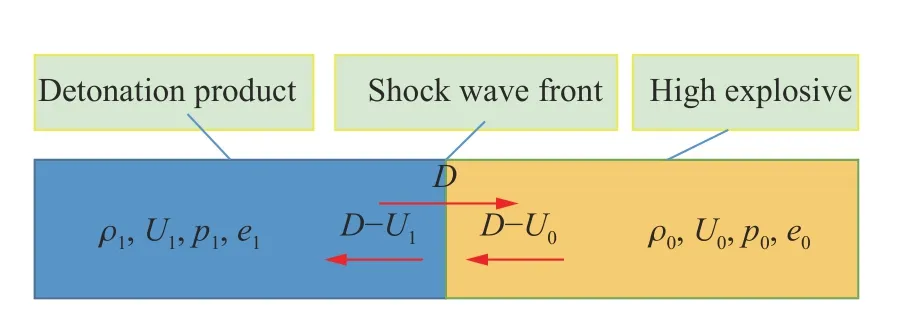
圖1 爆轟波在高能炸藥中的傳播示意圖Fig. 1 Sketch of propagation of detonation wave into high explosive

根據(jù)Hugoniot 守恒定律和C-J 假設(shè)，波陣面兩側(cè)物理量滿足如下關(guān)系。

(1) 質(zhì)量守恒：

(2) 動(dòng)量守恒：

(3) 能量方程：

(4) Chapman-Jouguet 假設(shè)：

(5) 聲速定義：

式中：v1=1/ρ1，為爆轟產(chǎn)物的比容；v0=1/ρ0，為未反應(yīng)炸藥的比容； ρ1為爆轟產(chǎn)物的密度；p1為波后壓力；U1為波后介質(zhì)速度；e1為爆轟產(chǎn)物的內(nèi)能；c為聲速；S代表等熵狀態(tài)。

對(duì)于高能炸藥，p0?p1，因而假設(shè)p0=0。由于爆轟波未到達(dá)時(shí)，圖1 右側(cè)高能炸藥近似認(rèn)為處于靜止?fàn)顟B(tài)，進(jìn)而假設(shè)U0=0。且高能炸藥反應(yīng)物和產(chǎn)物的EOS 均使用γ 律：

由式(1)～(6)導(dǎo)出波后介質(zhì)QoIs 的函數(shù)表達(dá)式：

式中：ρJ、pJ、UJ和cJ分別代表C-J 理論導(dǎo)出的爆轟產(chǎn)物的初始密度、壓力、速度和聲速。式(7)建立了C-J 狀態(tài)下波后介質(zhì)QoIs 和物理量D、ρ0以及唯象參數(shù)γ 的函數(shù)關(guān)系式。由于波后介質(zhì)物理量試驗(yàn)標(biāo)定困難且成本較高，因此式(7)成為預(yù)測(cè)波后介質(zhì)QoIs 的實(shí)用工具。

2 爆轟不確定因素的定量刻畫(huà)

受測(cè)量技術(shù)、含能材料自身固有屬性和人類(lèi)認(rèn)知的局限性等因素的影響，爆轟M&S 中的物理量和唯象參數(shù)均受到噪聲污染[12-14]。ρ0的不確定度主要來(lái)源于壓制成型時(shí)炸藥顆粒的扭結(jié)、隨機(jī)結(jié)晶、空洞和裂紋的存在以及雜質(zhì)的摻入；爆速D的不確定度主要來(lái)源于測(cè)量技術(shù)。即D和ρ0的不確定度與材料的固有屬性有關(guān)，即使增加樣本容量，不確定度也不會(huì)消失。

2.1 不確定物理量的表征

根據(jù)Wilkins 等[19]的理論，在爆轟計(jì)算中，合適的概率分布能合理描述含能材料密度的非均勻性。本文中，假設(shè)PBX-9502的初始密度服從對(duì)數(shù)正態(tài)分布，其中μ ?和 σ?分別為對(duì)數(shù)期望和對(duì)數(shù)標(biāo)準(zhǔn)差。與正態(tài)分布相比，對(duì)數(shù)正態(tài)分布的優(yōu)勢(shì)在于符合統(tǒng)計(jì)規(guī)律的同時(shí)能保證物理量的非負(fù)性。首先，利用浸液法測(cè)量炸藥的密度[20]，給出PBX-9502 初始密度的統(tǒng)計(jì)直方圖，如圖2 所示。根據(jù)矩估計(jì)法導(dǎo)出試驗(yàn)結(jié)果的期望μ=1.894 g/cm3和標(biāo)準(zhǔn)差σ=0.002 5 g/cm3。進(jìn)而，使用Anderson-Darling 假設(shè)檢驗(yàn)法，在5%顯著性水平下，ρ0接受服從對(duì)數(shù)正態(tài)分布的原假設(shè)。最后，通過(guò)曲線擬合技術(shù)，得到PBX-9502 的概率密度函數(shù)。如圖2 所示，初始密度的概率密度函數(shù)曲線與試驗(yàn)數(shù)據(jù)吻合很好。

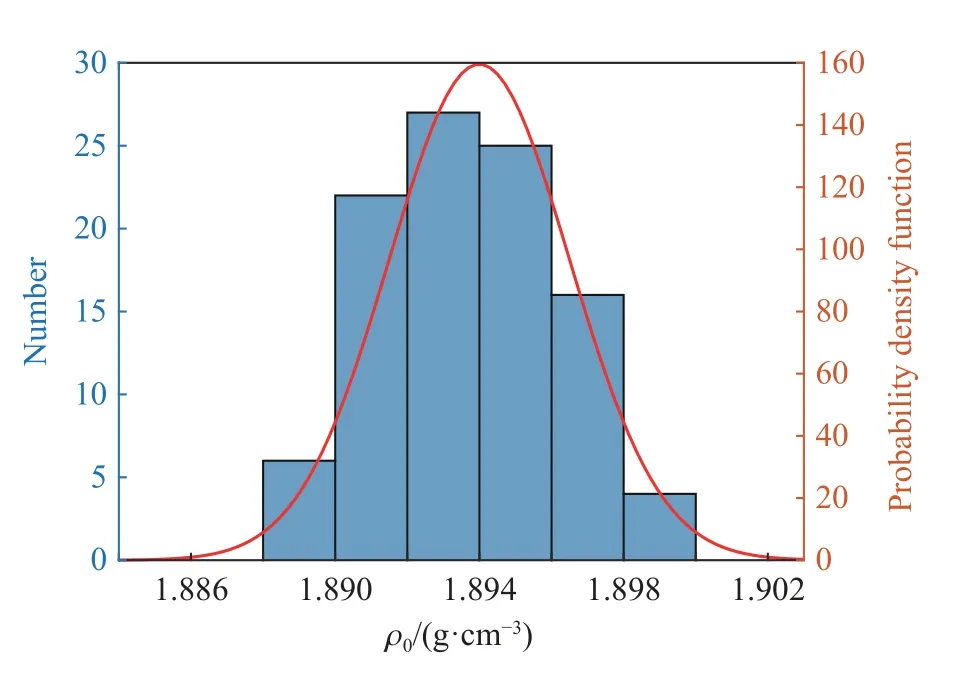
圖2 PBX-9502 初始密度的概率密度函數(shù)Fig. 2 PDF of initial density of PBX-9502

爆速是爆轟研究中唯一能使用較簡(jiǎn)單試驗(yàn)裝置和流程即可標(biāo)定的物理量，這里的試驗(yàn)結(jié)果來(lái)自于測(cè)時(shí)儀法[20]。假設(shè)D～，使用Anderson-Darling 假設(shè)檢驗(yàn)，驗(yàn)證得到：在5%顯著性水平下，D也接受服從對(duì)數(shù)正態(tài)分布的原假設(shè)。結(jié)合試驗(yàn)數(shù)據(jù)，使用矩估計(jì)法，導(dǎo)出爆速的期望μD=7710m/s，標(biāo)準(zhǔn)差σD=321m/s。代入式(8)，計(jì)算得到=8.9503，=0.0025。使用曲線擬合技術(shù)，得到PBX-9502 爆速的概率密度函數(shù)曲線如圖3 所示。

圖3 PBX-9502 爆速的概率密度函數(shù)Fig. 3 PDF of detonation velocity of PBX-9502

2.2 不確定的唯象參數(shù)

EOS 中的參數(shù)γ 無(wú)法通過(guò)試驗(yàn)直接標(biāo)定。由工程經(jīng)驗(yàn)和專(zhuān)家意見(jiàn)，假設(shè)γ～B[2.93, 2.99, 6, 6]，其中B[a,b,m,n] 代表4 參數(shù)Beta 分布，[a,b]表示參數(shù)的取值范圍，m、n表示形狀參數(shù)。根據(jù)經(jīng)驗(yàn)，形狀參數(shù)取m=6，n=6。與正態(tài)分布相比，Beta 分布的優(yōu)點(diǎn)在于取值范圍有界。與均勻分布相比，Beta 分布的PDF 曲線光滑而不間斷。γ 的PDF 的詳細(xì)信息如圖4 所示。

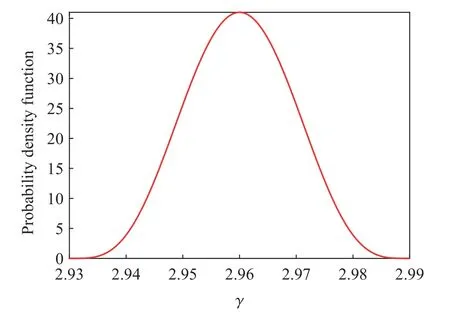
圖4 多方指數(shù)γ 的概率密度函數(shù)Fig. 4 PDF of polytrophic exponent γ

3 不確定度傳播方法

3.1 高維非嵌入多項(xiàng)式混沌

設(shè) ξ=(ξ1,ξ2,···,ξd)T是概率空間 ( ?,F,P) 中的d維獨(dú)立標(biāo)準(zhǔn)正態(tài)隨機(jī)向量，其中Ω為樣本空間，F(xiàn)為定義在Ω上的σ-代數(shù)，P為概率測(cè)度。L2(Ω)為Ω上的平方可積函數(shù)空間，設(shè)u∈L2(?) 代表爆轟系統(tǒng)的QoI。若賦予內(nèi)積：

式中： ω ∈? 代表基本事件， ρ(x)=(2π)-d/2e-xTx/2為隨機(jī)向量 ξ 的聯(lián)合概率密度函數(shù)，則L2(?) 構(gòu)成Gauss-Hilbert 空間。利用Cameron-Martin 定理[17]，u可以通過(guò) ξ 的正交多項(xiàng)式展開(kāi)：

隨機(jī)基函數(shù)：

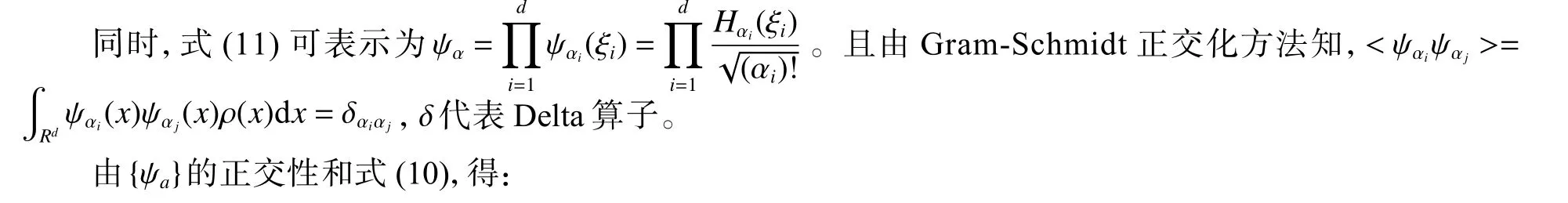
當(dāng)d=1 時(shí)，由式(10)、(13)和Hermite-Gauss 求積公式，得到：

式中：ξr、wr分別為求積點(diǎn)和權(quán)重。本文中取S=6，此時(shí)，Hermite-Gauss 積分的求積點(diǎn)和權(quán)重如表1 所示。

表1 6 節(jié)點(diǎn)Hermite-Gauss 積分的求積點(diǎn)和權(quán)重[21]Table 1 Quadrature points and weights for Hermite-Gauss integration with six points[21]

當(dāng)d＞1 時(shí)，使用全張量積Hermite-Gauss 求積公式，即：

實(shí)際應(yīng)用中，式(10)通常截?cái)酁椋?/p>

3.2 Rosenblatt 變換

由第2 節(jié)知，輸入不確定度不服從標(biāo)準(zhǔn)正態(tài)分布且概率類(lèi)型不一致，因此無(wú)法直接使用3.1 節(jié)所述PC 理論。本文中使用Rosenblatt 變換將一列相關(guān)隨機(jī)變量轉(zhuǎn)化成一列服從標(biāo)準(zhǔn)正態(tài)分布的獨(dú)立隨機(jī)變量。具體步驟為：

設(shè)X=(X1,X2,···,Xd)T為d維非高斯隨機(jī)向量，令FX(x1,x2,···,xd)為X的聯(lián)合累積分布函數(shù)(cumulative density function, CDF)。構(gòu)造如下映射關(guān)系Y=G(X)[22]：

式中：Fxd(xd|x1,x2,···,xd-1) 為條件CDF， Φ 為標(biāo)準(zhǔn)正態(tài)變量的CDF，則Y服從獨(dú)立標(biāo)準(zhǔn)正態(tài)分布。

4 結(jié)果的UQ 分析

利用3.2 節(jié)Rosenblatt 變換技術(shù)將第2 節(jié)標(biāo)定的輸入不確定度D、ρ0和γ 轉(zhuǎn)化為相互獨(dú)立的標(biāo)準(zhǔn)正態(tài)分布。然后利用3.1 節(jié)非嵌入PC 結(jié)合式(7)計(jì)算波后QoIs 的概率密度函數(shù)。具體流程如圖5 所示。

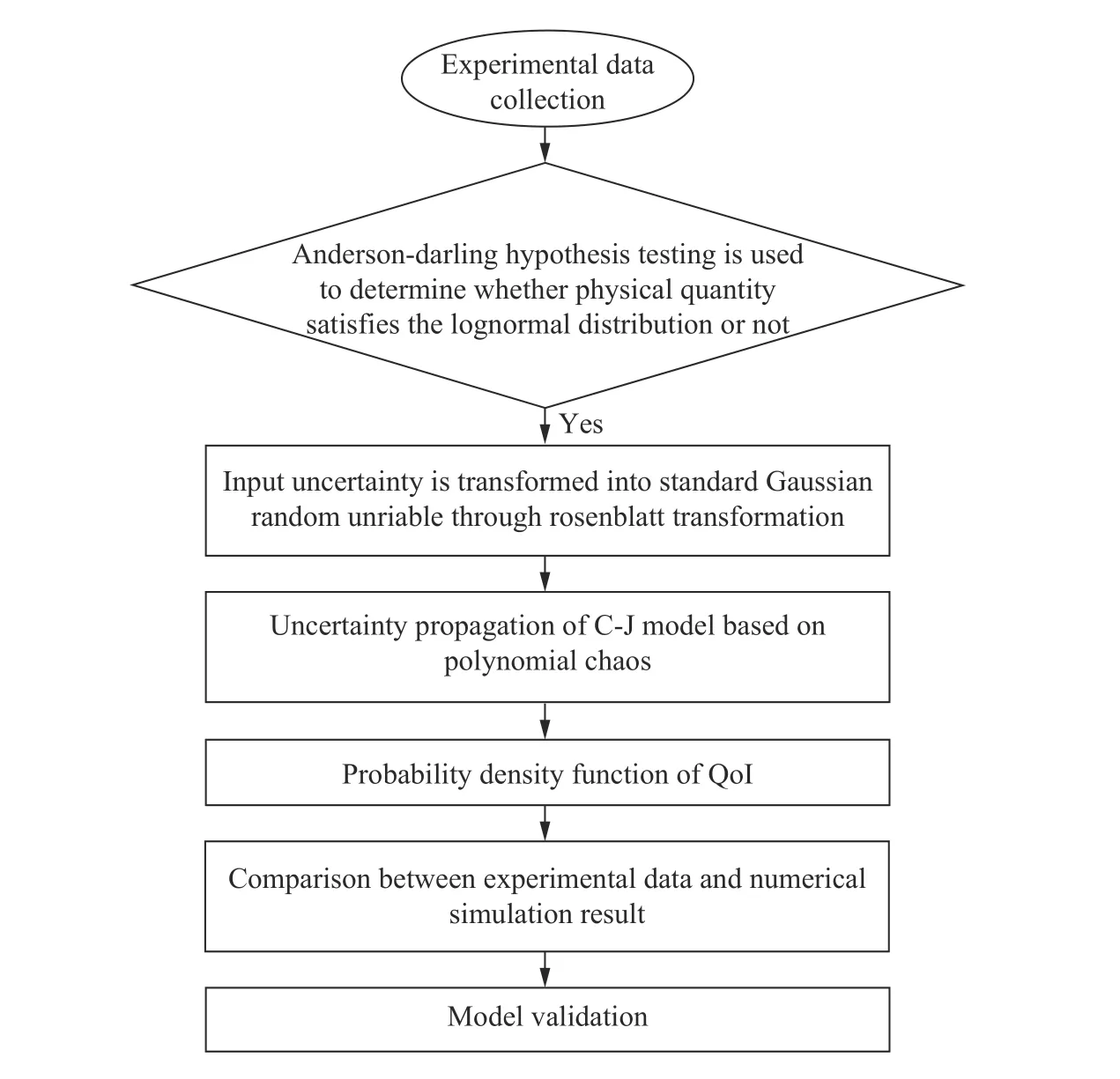
圖5 不確定分析算法流程圖Fig. 5 Flow chart of uncertainty analysis

本文中，d=3，Q=3，因此K=20。接著利用表1，構(gòu)造二維全張量Hermite-Gauss 積分求積點(diǎn)，如圖6所示。本文中計(jì)算將會(huì)用到的前6 階Hermite 多項(xiàng)式的具體形式如圖7 所示。結(jié)合式(1)～(7) 和(15)～(16)，利用圖5 所示的不確定度分析流程計(jì)算出QoIs 的概率密度函數(shù)，更多信息如圖8 所示。可以看出，波后QoIs 的概率密度函數(shù)沒(méi)有明顯的對(duì)稱(chēng)性，且峰度指標(biāo)均大于3，處于尖峰狀態(tài)，不服從Gauss 分布。特別是波后密度，峰度指標(biāo)最大，曲線最尖峭，且具有明顯的偏差，與正態(tài)分布差別很大。波后壓力的峰度系數(shù)最小，對(duì)稱(chēng)性最好，形狀最接近正態(tài)分布，可用正態(tài)分布近似替代。

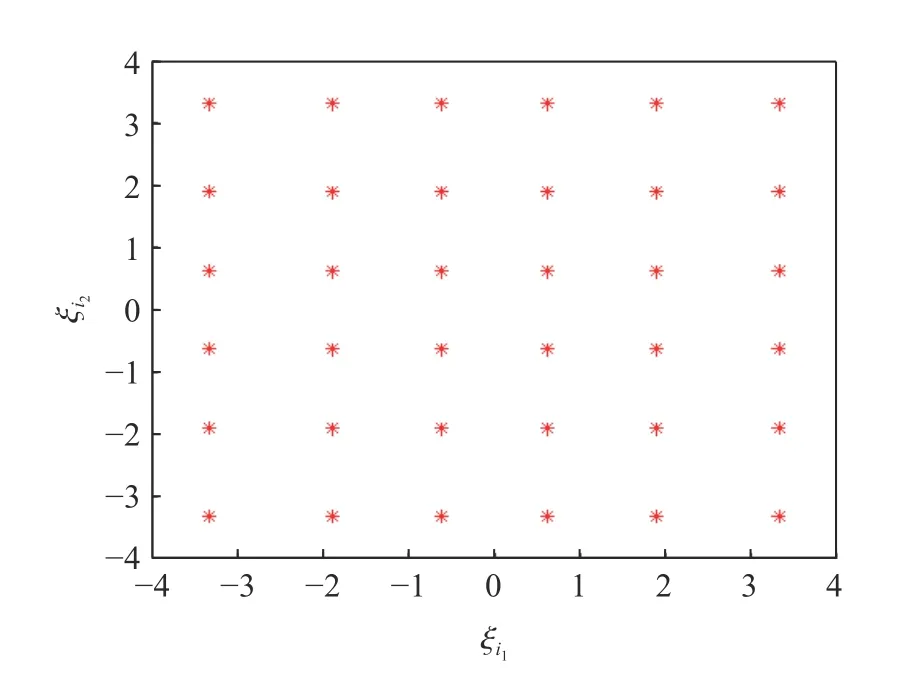
圖6 二維全張量積Gauss-Hermite 求積點(diǎn)的位置Fig. 6 Locations of Gauss-Hermite quadrature points used for two-dimensional tensor product

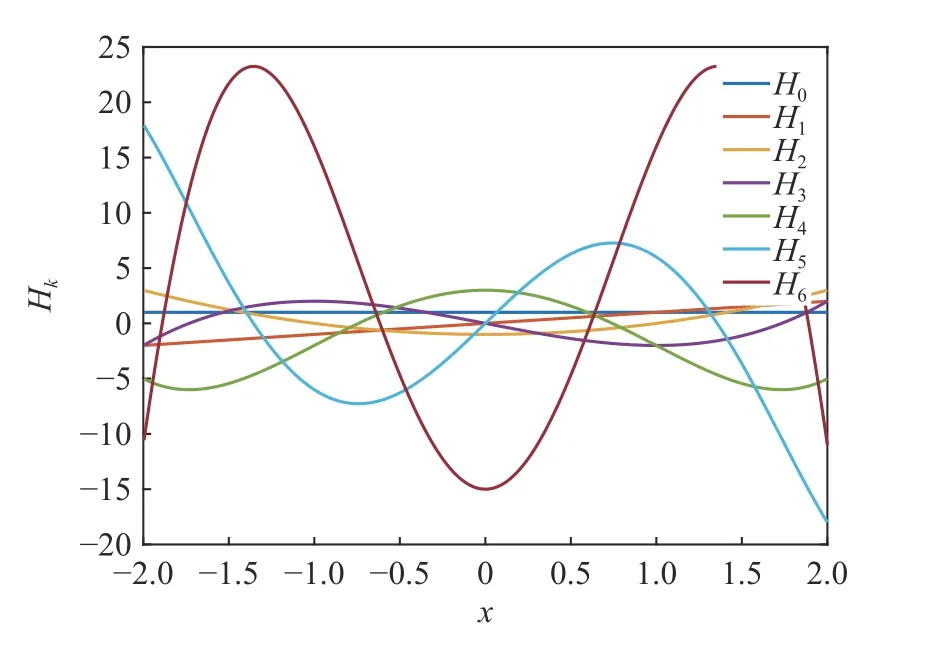
圖7 前6 階單變量Hermite 多項(xiàng)式Fig. 7 The first six orders of univariate Hermite polynomials

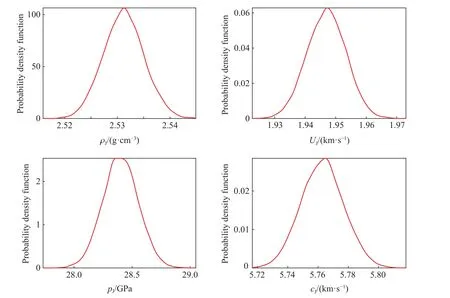
圖8 系統(tǒng)響應(yīng)量的概率密度函數(shù)Fig. 8 PDF of system response quantities

此外，QoIs 的統(tǒng)計(jì)量，如期望和方差，可通過(guò)uα顯性表達(dá)，即：

利用式(18)計(jì)算出波后QoIs 的期望，標(biāo)準(zhǔn)差，具體內(nèi)容見(jiàn)表2。從表2 可以看出，波后介質(zhì)密度的標(biāo)準(zhǔn)差與期望的比值小于5%，而波后介質(zhì)壓力的標(biāo)準(zhǔn)差與期望的比值大于5%。波后介質(zhì)壓力波動(dòng)較大，取值較寬，與文獻(xiàn)[6, 23]的“爆轟壓力測(cè)量值分散性較大”的結(jié)論相吻合。

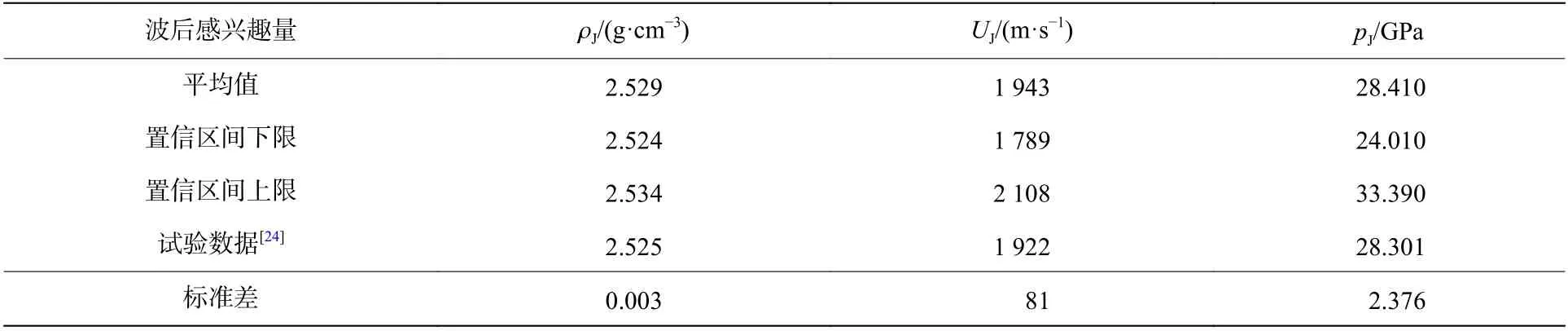
表2 波后感興趣量的試驗(yàn)和統(tǒng)計(jì)結(jié)果Table 2 Statistical and experimental result of QoIs at the rear of the shock wave

根據(jù)圖8 信息，可計(jì)算出95%置信水平下波后QoIs 的置信區(qū)間。同時(shí)，波后介質(zhì)的壓力、密度和速度等物理量也能通過(guò)試驗(yàn)標(biāo)定[6,23]。數(shù)值預(yù)測(cè)結(jié)果與洛斯阿拉莫斯國(guó)家實(shí)驗(yàn)室（Los Alamos National Laboratory, LANL）的試驗(yàn)結(jié)果[24]作比對(duì)。比較發(fā)現(xiàn)，波后介質(zhì)的壓力、密度和速度的試驗(yàn)數(shù)據(jù)落入95%置信水平下的置信區(qū)間內(nèi)，進(jìn)一步確認(rèn)了方法的有效性。

5 結(jié)果與討論

C-J 理論建立了波后介質(zhì)壓力、速度、聲速和密度等系統(tǒng)響應(yīng)量和初始密度、爆速以及多方指數(shù)的顯式函數(shù)關(guān)系。初始密度易于測(cè)量，爆速也容易通過(guò)較簡(jiǎn)單的試驗(yàn)標(biāo)定。C-J 理論成為試驗(yàn)之外的波后物理量標(biāo)定手段，成本低，實(shí)用性強(qiáng)。

本文中，在概率框架下研究C-J 理論，結(jié)果以PDF 表征，允許QoIs 在一定范圍內(nèi)變動(dòng)。首先給出了輸入不確定度的定量表征，使用Anderson-Darling 假設(shè)檢驗(yàn)法驗(yàn)證概率假設(shè)的正確性。運(yùn)用收斂速度更快的非嵌入PC 結(jié)合Rosenblatt 變換研究了輸入不確定度對(duì)波后QoIs 的影響，發(fā)現(xiàn)試驗(yàn)結(jié)果落入QoIs 的置信區(qū)間內(nèi)。這說(shuō)明密度、爆速等物理量在生產(chǎn)、加工和測(cè)試過(guò)程中的正常擾動(dòng)不影響C-J 理論的使用。同時(shí)，模型也允許多方指數(shù)在一定范圍內(nèi)變動(dòng)。基于C-J 理論的爆轟UQ 結(jié)果能為裝藥設(shè)計(jì)、裝甲防護(hù)等提供決策依據(jù)。方法具有普遍性，能推廣到其他狀態(tài)方程描述的爆轟UQ 研究。

下一步擬減少假設(shè)、簡(jiǎn)化和近似的使用次數(shù)，將C-J 理論UQ 研究推廣到更加復(fù)雜的情況，如非γ 律EOS，甚至推廣到ZND 理論的UQ 研究。對(duì)于非理想爆轟，聲速面后可能存在放能。引入放能后，預(yù)測(cè)結(jié)果的差異，即不同模型導(dǎo)致的不確定度，也叫模型形式不確定度量化。這是國(guó)際熱點(diǎn)，也是不確定度量化領(lǐng)域的難點(diǎn)之一。

另外，本文中，研究沿用Oberkampf 的思路[25]，即將試驗(yàn)結(jié)果看作是基準(zhǔn)的，用以評(píng)估模擬結(jié)果的可信度。事實(shí)上，QoIs 的試驗(yàn)結(jié)果也受到不確定因素的擾動(dòng)，下一步擬綜合試驗(yàn)不確定度和數(shù)值模擬不確定度開(kāi)展研究。同時(shí)，從爆轟研究角度看，更希望從包含不確定度的某一參數(shù)實(shí)測(cè)結(jié)果中通過(guò)統(tǒng)計(jì)分析得到盡量多相關(guān)參數(shù)的均值和標(biāo)準(zhǔn)差等信息。若能指導(dǎo)實(shí)驗(yàn)設(shè)計(jì)方法，用盡量少的實(shí)驗(yàn)次數(shù)得到QoIs 的結(jié)果，是另一個(gè)值得探討的課題。