基于自抗擾控制的分布式鉸接車輛轉向控制

曹國棟，王鐵，吉志勇，馬好娜，劉兆基

(太原理工大學車輛工程系，山西太原 030024)

0 前言

隨著國內外智能駕駛技術的快速發展，為保障礦運車輛安全、可靠地行駛，無人駕駛礦運車輛應運而生。分布式鉸接車輛作為礦運車輛的典型代表，具有承載能力高、機動性強、成本低等特點，在實際運輸作業中被廣泛應用。然而，鉸接車輛通過兩車體間的相對運動實現轉向，轉向過程中整車姿態持續變化，因此轉向穩定性差、路徑跟蹤困難。

近年來，為提高鉸接車輛路徑跟蹤控制精度，在深入研究其非線性動力學特性的基礎上，發展出多種鉸接車輛路徑跟蹤控制技術，典型的控制方法有比例-積分-微分(PID)控制、模糊控制(Fuzzy Control)、最優控制、模型預測控制(Model Predictive Control，MPC)等[1-2]。文獻[3]設計出不依賴鉸接車輛精確模型的PID路徑跟蹤器；文獻[4]設計了模糊控制器，并以PID控制器為對照組，進一步縮短了鉸接車輛進入穩定轉向狀態的時間；文獻[5]提出基于線性二次型調節器(Linear Quadratic Regulator，LQR)的鉸接車路徑跟蹤控制器，雖然該控制器的魯棒性較強，但不能適應路徑曲率變化較大的路況；文獻[6]基于線性化的鉸接車輛三自由度動力學模型，應用模型預測控制器對鉸接車輛的轉向驅動力矩進行控制，提高了車輛在縱向車速恒定狀態下的路徑跟蹤精度，但是沒有考慮鉸接車輛的非線性動態特性。在建立鉸接車輛路徑跟蹤控制器過程中，通常將液壓轉向系統等效為轉向驅動力矩，很少考慮轉向系統自身特性對鉸接車輛行駛穩定性的影響。

轉向系統的核心是在滿足轉向穩定性的前提下，靈活改變車輛的行駛方向。由于鉸接車輛轉向阻力矩較大，通常采用液壓轉向系統提供轉向驅動力矩[7]。文獻[8]建立了基于PID控制的雙閥控非對稱缸液壓轉向系統仿真模型，并通過試驗證明了所建模型的準確性；文獻[9]建立了基于二自由度拖拉機動力學模型的液壓轉向系統模糊控制器，將車輛轉向角度誤差控制在0.017 rad以內；文獻[10]針對液壓系統擾動的不確定性，設計了基于模糊滑模控制的全液壓轉向系統控制器，在一定程度上抑制了轉向控制系統的抖動，提高了液壓轉向系統的魯棒性。上述文獻在建立液壓轉向系統模型過程中，對流量-壓力特性進行了線性化處理，無法反映液壓系統的非線性動力學特性；同時，沒有考慮前饋控制，不能及時消除系統擾動，降低了液壓轉向系統的抗擾動性能。

ADRC(Active Disturbance Rejection Control )控制器繼承了PID控制器基于誤差來消除誤差的核心思想，采用擴張狀態觀測器測量并消除被控對象中的各種非線性干擾后，形成一個積分串聯型PID控制器，提高控制系統穩定性[11-12]。鉸接車輛轉向時受轉向阻力矩變化、質心位置偏移和路面不平度等非線性干擾的影響[13-14]，可采用ADRC控制器提高車輛的抗擾動性能。

本文作者首先建立包括車身模型、輪胎模型和液壓轉向系統模型在內的鉸接車輛11自由度非線性動力學模型，而后設計了考慮鉸接車輛轉向時轉向阻力矩變化、質心位置偏移和路面不平度等非線性干擾因素的自抗擾控制器(ADRC)，最后通過MATLAB/Simulink仿真驗證所設計的液壓轉向控制系統的性能。

1 分布式鉸接車輛動力學建模

1.1 車身動力學模型

為研究鉸接車輛行駛過程中前后車體各自的運動狀態，對其兩車體進行如圖1所示受力分析。

圖中：OXY為絕對坐標系；O1X1Y1為原點固結在前車體質心上的隨動坐標系，X1軸與前車體縱向軸線重合；O2X2Y2為原點固結在后車體質心上的隨動坐標系，X2軸與后車體縱向軸線重合；ui為車體質心縱向速度(i=1，2)；vi為車體質心側向速度(i=1，2)；Fxij為輪胎縱向力(i=1，2；j=1，2)；Fyij為輪胎側向力(i=1，2；j=1，2)；Ti為轉向驅動力矩(i=1，2)；Rx為鉸接點處沿車體縱向軸線方向作用力；Ry為鉸接點處沿車體側向軸線方向作用力；γ1為前車體質心處橫擺角速度；γ2為后車體質心處橫擺角速度；L11為鉸接點至前車體質心距離；L12為前車體質心至前橋距離；L21為鉸接點至后車體質心距離；L22為后車體質心至后橋距離；Lf為前車體輪距；Lr為后車體輪距。其中：(i=1,2)分別表示前車體和后車體；(j=1，2)分別表示車體左側和右側。

鉸接車輛兩車體質心間的運動學關系為

(1)

依據牛頓-歐拉法對前后車體進行動力學分析可知，前車體和后車體質心處的縱向運動、橫向運動和橫擺運動的表達式分別為式(2)和式(3)：

(2)

(3)

式中：I1、I2分別為前車體和后車體的轉動慣量；T1、T2分別為前車體和后車體的轉向驅動力矩；m1、m2分別為前車體和后車體的質量。

聯立式(1)—(3)可得X=[u1，v1，u2，v2，γ1，γ2]為狀態變量、u=[Fx11，Fx12，Fx21，Fx22，Fy11，Fy12，Fy21，Fy22]為輸入、Y=[u1，v1，u2，v2，γ1，γ2]為輸出的非線性鉸接車輛車身動力學模型。

1.2 液壓轉向系統模型

鉸接車輛液壓轉向系統采用恒壓油源，主要由三位四通比例換向閥和兩個非對稱液壓缸組成，結構簡圖如圖2所示。

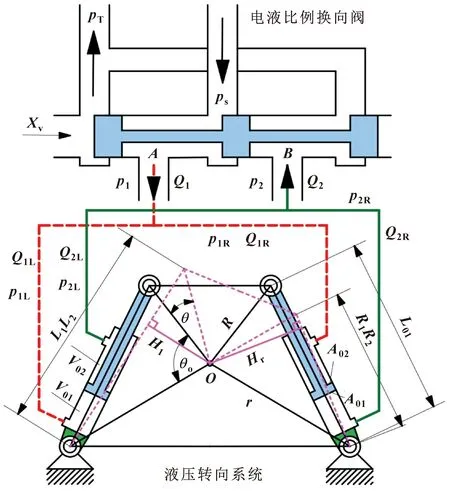
圖2 鉸接車輛液壓轉向系統結構簡圖

圖中：ps為液壓系統油源供油壓力；pT為液壓系統回油壓力；p1、p2分別為換向閥A口和B口壓力；p1L、p2L分別為左側液壓缸無桿腔和有桿腔壓力；p1R、p2R分別為右側液壓缸有桿腔和無桿腔壓力；Q1、Q2分別為換向閥A口和B口流量；Q1L、Q2L分別為左側液壓缸無桿腔和有桿腔流量；Q1R、Q2R分別為右側液壓缸有桿腔和無桿腔流量；A01、A02分別為液壓缸無桿腔和有桿腔工作面積；V01、V02分別為液壓缸無桿腔和有桿腔初始容積；θ0為兩側液壓缸初始安裝角；θ為鉸接車轉向角度；L01為兩側液壓缸初始長度；L1L2、R1R2分別為左側液壓缸和右側液壓缸實時工作長度；R、r分別為鉸接點至液壓缸與前、后車體連接點距離；Hl、Hr分別為左側液壓缸和右側液壓缸對鉸接點O的作用力臂。

液壓缸在車體兩側對稱布置，通過改變換向閥的閥芯位移，調整液壓油流入液壓缸的流量和方向，控制車輛轉向行駛。車輛轉向過程中，液壓缸實時長度為

(4)

液壓缸活塞桿位移量為

(5)

液壓缸作用力臂為

(6)

液壓桿位移和鉸接角間的運動學關系：

(7)

換向閥A閥口和B閥口的流量分別為：

(1)閥芯位移Xv> 0時，鉸接車輛正向轉向

(8)

(9)

式中：Cd為流量系數；ω為面積梯度；ρ為液體密度。

(2)閥芯位移Xv<0時，鉸接車輛反向轉向

(10)

其中：Q1=Q1L+Q1R；Q2=Q2L+Q2R。

鉸接車輛轉向時，液壓缸流量連續方程為

(11)

式中：βe為體積彈性模量；液壓缸內泄漏系數Cip和液壓缸外泄漏系數Cep取值均為5×10-3；A01=3.10×10-3m2，A02=2.20×10-3m2，V01=4.39×10-4m3，V02=3.42×10-4m3。

轉向驅動力矩和液壓缸壓力之間的關系為

T1=(A01Hl+A02Hr)p1-(A02Hl+A01Hr)p2-

sign(Xv)Tt

(12)

式中：Tt為轉向阻力矩。

鉸接車輛空載轉向時，前車體質量小，以前車體轉向為主，轉向阻力矩為

(13)

式中：L=L11+L12；L=L11+L12+L21+L22；n為系數；μ為滑動附著系數；Lw為輪胎寬度；f為滾動阻力系數。

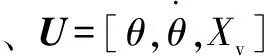
1.3 Fiala輪胎模型

Fiala非線性輪胎模型將胎體與路面之間的相互作用關系簡化為彈性梁結構，具有計算量小、通用性強的特點[15]。該模型中的縱向滑移率Sx與縱向力Fx間的關系為

(14)

式中：Kx為輪胎縱滑剛度；Ss為輪胎縱向滑移率；Ssc為輪胎接地印記內縱向滾滑臨界點；μ1為復合摩擦因數；Fz為輪胎垂向力。

側偏角α與側向力Fy間的關系為

(15)

2 ADRC控制器設計

ADRC控制器由跟蹤-微分器(TD)、非線性誤差反饋控制律(NLSEF)和非線性擴張狀態觀測器(NLESO)組成。首先應用跟蹤-微分器對輸入的轉向控制信號進行跟蹤和濾波，然后應用非線性擴張狀態觀測器對鉸接車輛的運動狀態和運動干擾量進行觀測，最后將兩者的輸出信號輸送至非線性誤差反饋控制律中，經運算后輸出液壓轉向系統控制信號Xv。

2.1 跟蹤-微分器

跟蹤-微分器的主要作用是快速、無超調地跟蹤期望轉向角度和期望轉向角速度控制信號，并對兩控制信號起到一定的濾波作用，降低控制信號的噪聲干擾，提高控制信號穩定性。其跟蹤算法為

(16)

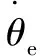
最速綜合函數fhan(·)的算法為

(17)

其中：

(18)

(19)

式(18)中：θt為期望轉向角度。

2.2 非線性誤差反饋控制律

非線性誤差反饋控制律為非線性的比例-微分(PD)組合，其控制參數可以在既定的變動范圍內進行非線性組合，從而達到更高的控制要求。此算法中應用的非線性函數fal(·)為

(20)

式中：i=1，2，3，4；ai為非線性函數控制參數；di為線性區間的長度。

非線性誤差反饋控制算法為

(21)

2.3 非線性擴張狀態觀測器

ADRC控制器的核心是非線性擴張狀態觀測器：一方面，通過它可以計算出鉸接車輛實際轉向角度和轉向角速度的觀測值，并將結果引入非線性誤差反饋控制律中形成閉環控制；另一方面，液壓轉向系統中的流量、壓力、工作溫度、機械磨損等內部狀態變量和路面不平度、前后車體相對運動干涉等外部狀態變量，被統一作為擾動量ω(k)，前饋至非線性誤差反饋控制律中消除。非線性擴張狀態觀測器的主要算法為

(22)

依據上述數學模型，在MATLAB/Simulink中搭建的ADRC控制器如圖3所示。

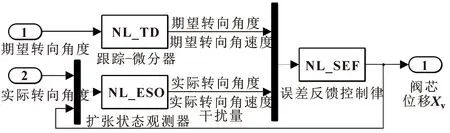
圖3 ADRC控制器結構

3 分布式鉸接車輛轉向特性仿真分析

3.1 整車仿真模型

分布式鉸接車輛整車模型主要包括非線性車身動力學模型、非線性液壓轉向系統動力學模型、非線性輪胎模型和液壓轉向系統控制器，該模型包括前車體速度閉環控制和整車轉向角度閉環控制。在MATLAB/Simulink中搭建的仿真模型如圖4所示。

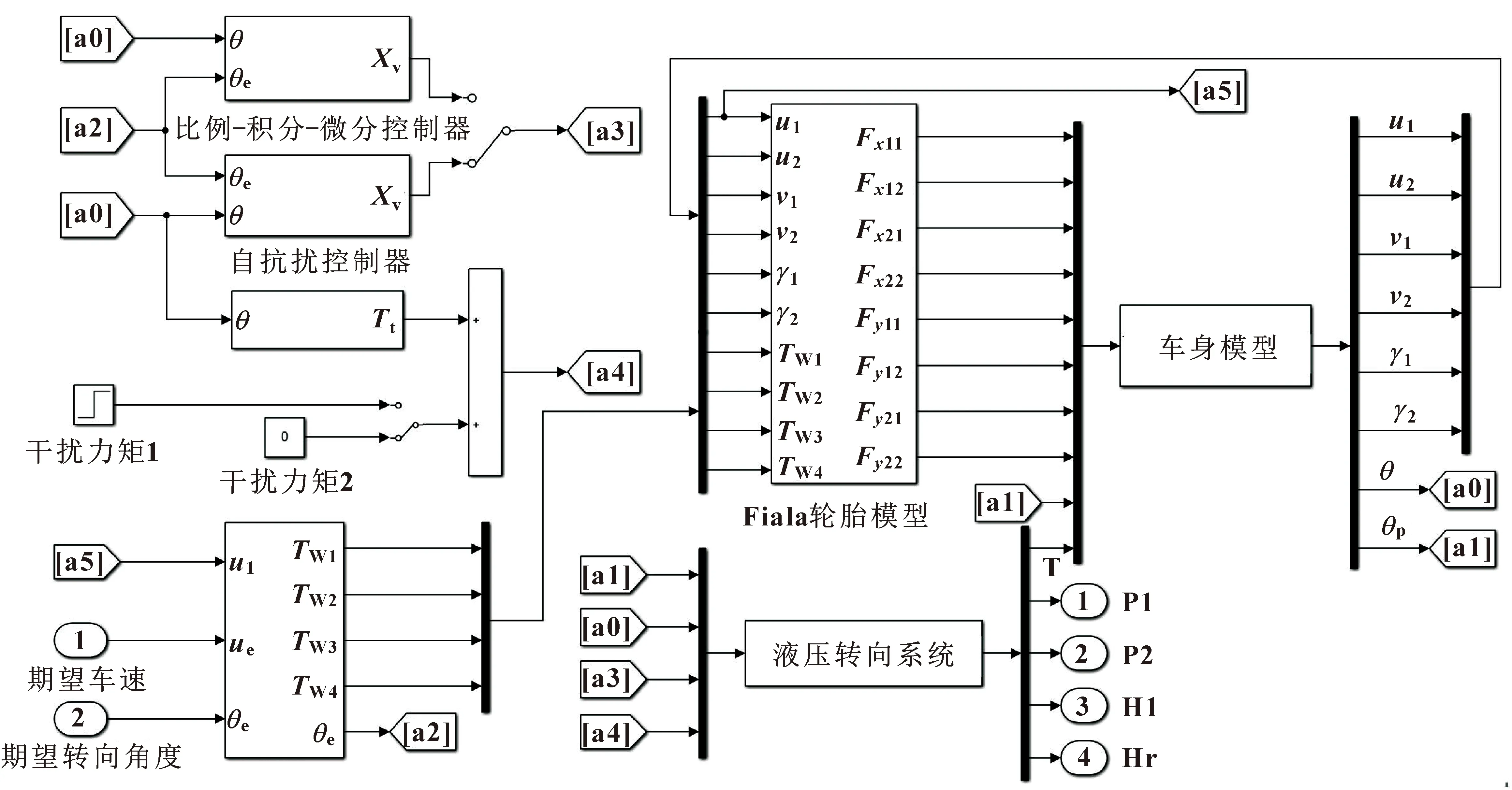
圖4 鉸接車輛整車仿真模型

3.2 鉸接車輛轉向特性仿真分析

為驗證ADRC控制器在鉸接車輛液壓轉向控制系統中的應用效果，分析鉸接車輛的轉向特性，基于上述模型，分別采用ADRC控制器和PID控制器作為液壓轉向系統控制器，進行初始車速為2.5 m/s的轉向分析。前車體質心在絕對坐標系中的運動軌跡如圖5所示，PID參數取KP=10、KI=0.02、KD=0.02，液壓轉向系統主要參數如表1所示，ADRC控制器參數如表2所示。

表1 液壓系統主要參數

表2 ADRC控制器參數

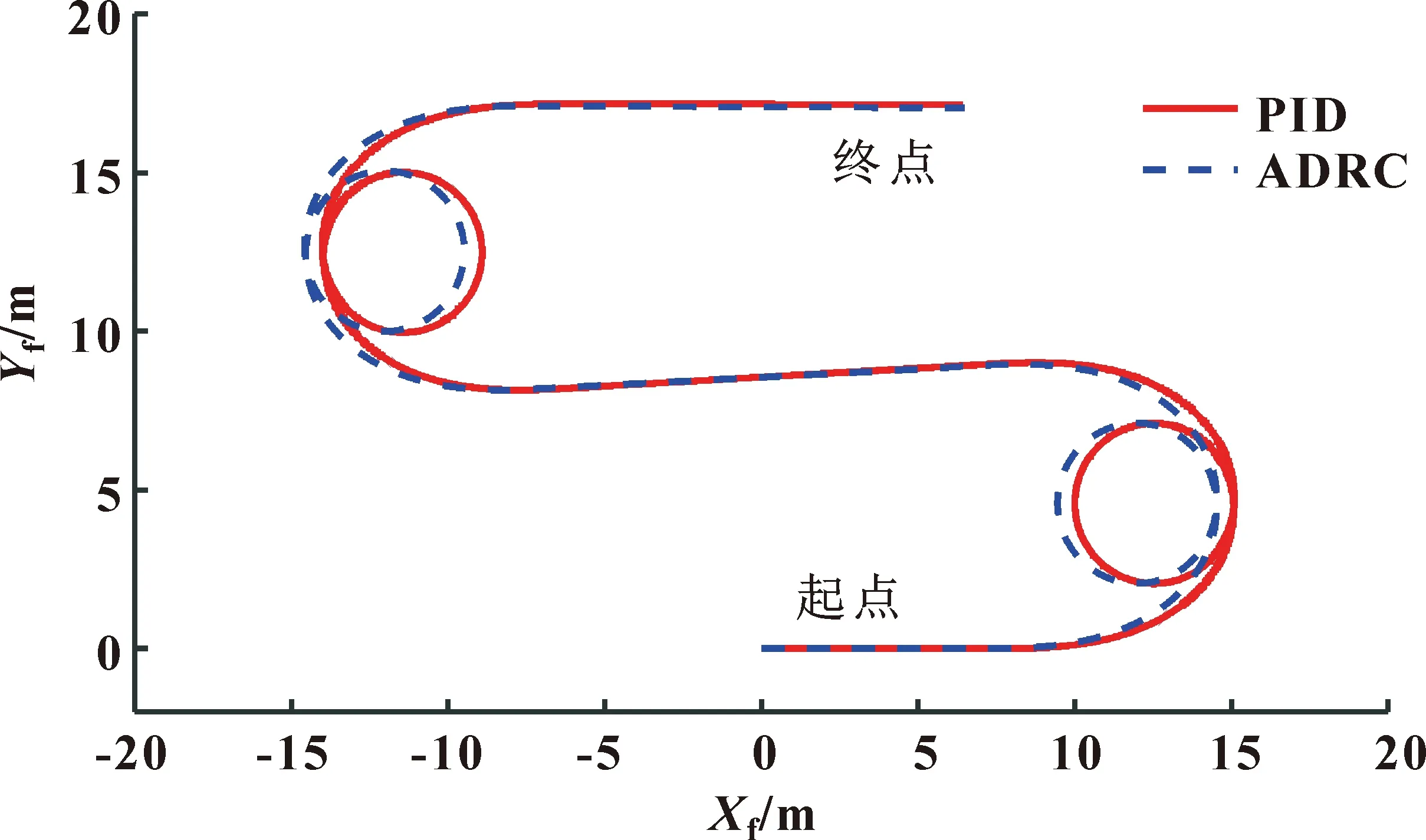
圖5 前車體質心運動軌跡

(1)鉸接車輛轉向運動學分析

仿真過程中，0～5 s內車輛處于擺正位，轉向角度為0 rad，此階段控制車速由0 m/s提升至2.5 m/s左右；5 s后車輛進行轉向行駛，最大轉向角度為0.8 rad。鉸接車輛的運動學狀態如圖6所示。

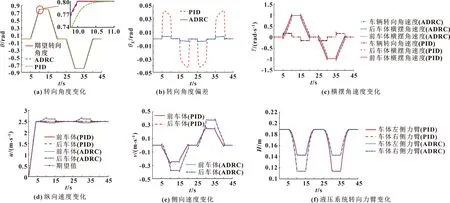
圖6 鉸接車輛運動學分析

由圖6知：5～10 s內鉸接車輛轉向角度由0 rad轉至0.8 rad，轉向角速度為0.16 rad/s，與預設轉向角速度基本相符，前后車體的橫擺角速度數值均逐漸增大，差值在0.14～0.16 rad/s間；為達到預設轉向角速度，后車體縱向速度上升，由于驅動力跟蹤滯后，前車體縱向速度下降；前車體側向速度下降，后車體側向速度先上升后下降；轉向系統兩側的轉向力臂長度呈逐漸減小趨勢，且左側轉向力臂長于右側，符合鉸接車輛前后車體相對轉動的特點。10～15 s內車輛的轉向角度穩定在0.8 rad，其他狀態曲線均保持平穩。15～20 s內車輛轉向角度仍以0.16 rad/s回轉至0 rad，各狀態曲線變化趨勢與5～10 s內相反，25～40 s內車輛運動狀態與5～20 s內相反。結果表明：相對于PID控制，基于ADRC控制的液壓轉向系統同樣可以滿足鉸接車輛0.8 rad轉向角度需求，車輛轉向角度調整更快，轉向角度實時跟蹤誤差更小，控制在0.017 rad以內，當期望轉向角度曲率改變后，車輛在0.1 s左右進入穩定行駛狀態，轉向角度控制精度更高。

(2)鉸接車輛轉向動力學分析

鉸接車輛轉向過程中所受作用力主要有轉向阻力矩、前后車體側向力、轉向驅動力矩和車體兩側的液壓缸壓力，各作用力變化趨勢如圖7所示。

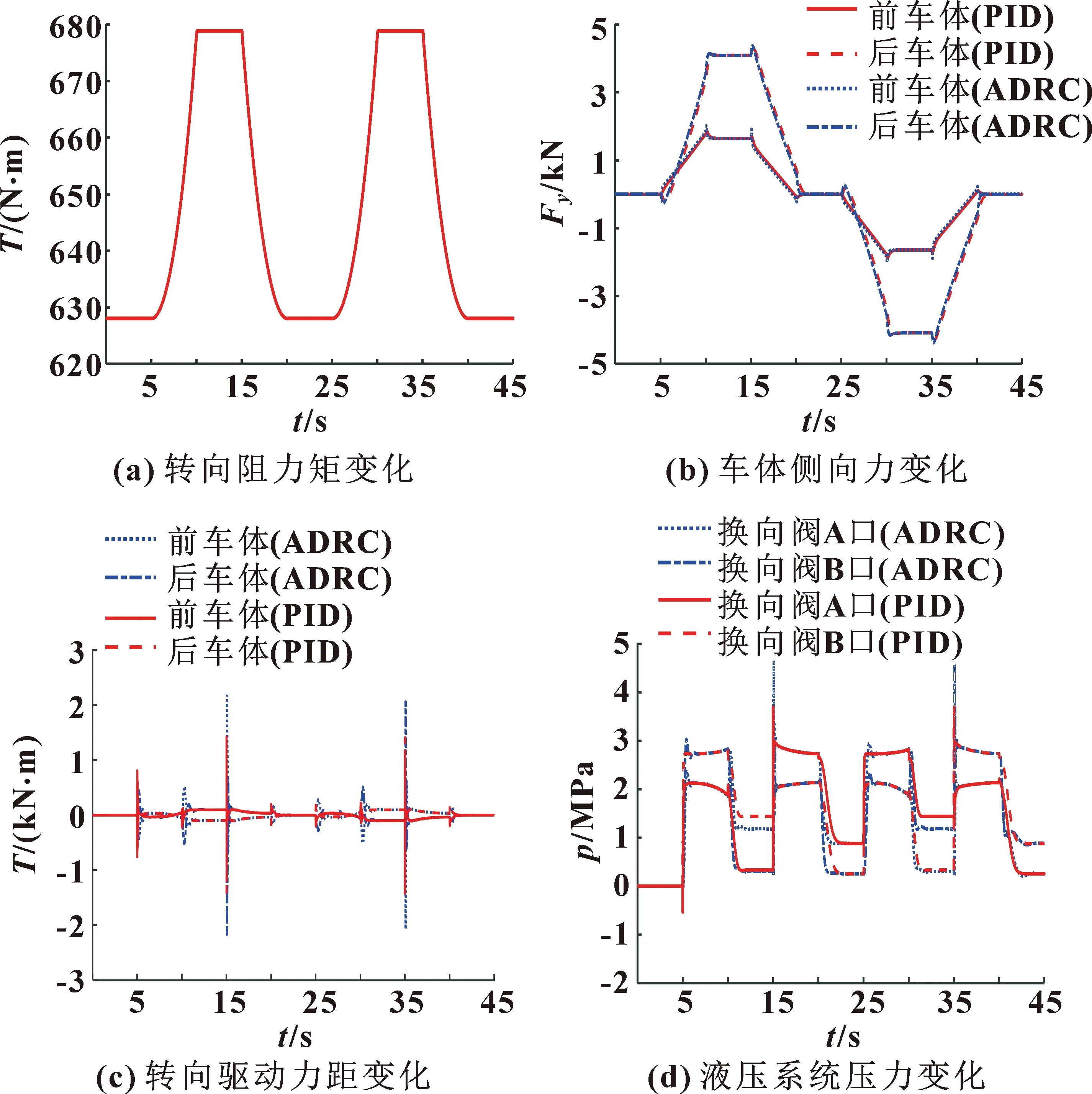
圖7 鉸接車輛動力學分析

結合圖6與圖7可知：鉸接車輛直線行駛時，轉向阻力矩最小，兩車體的側向力和轉向驅動力矩在0值附近，液壓缸壓力差基本穩定，用于抵消轉向阻力矩，維持鉸接車輛直線行駛狀態；轉向行駛時，隨著轉向角度的增加，轉向阻力矩逐漸增大，前后車體的側向力、車輛兩側液壓缸的壓差均逐漸增大，前車體轉向驅動力矩值呈上升趨勢，后車體轉向驅動力矩與前車體等大反向，相對于PID控制，基于ADRC控制下的車體側向力、轉向驅動力矩和液壓缸壓力調整速度更快，同時波動也較明顯；車輛以最大轉向角度穩定轉向時，各作用力狀態穩定，液壓轉向系統動力學穩定性好。

3.3 ADRC與PID控制下的轉向穩定性對比分析

為研究液壓轉向系統控制精度對鉸接車輛行駛穩定性的影響，以前文所述仿真條件為基礎，在第12 s時加入500 N·m轉向干擾力矩Tf，然后分別基于ADRC控制器和PID控制器進行鉸接車輛轉向抗干擾能力仿真分析。轉向干擾力矩信號如圖8所示，液壓轉向系統運動學與動力學仿真結果如圖9所示。

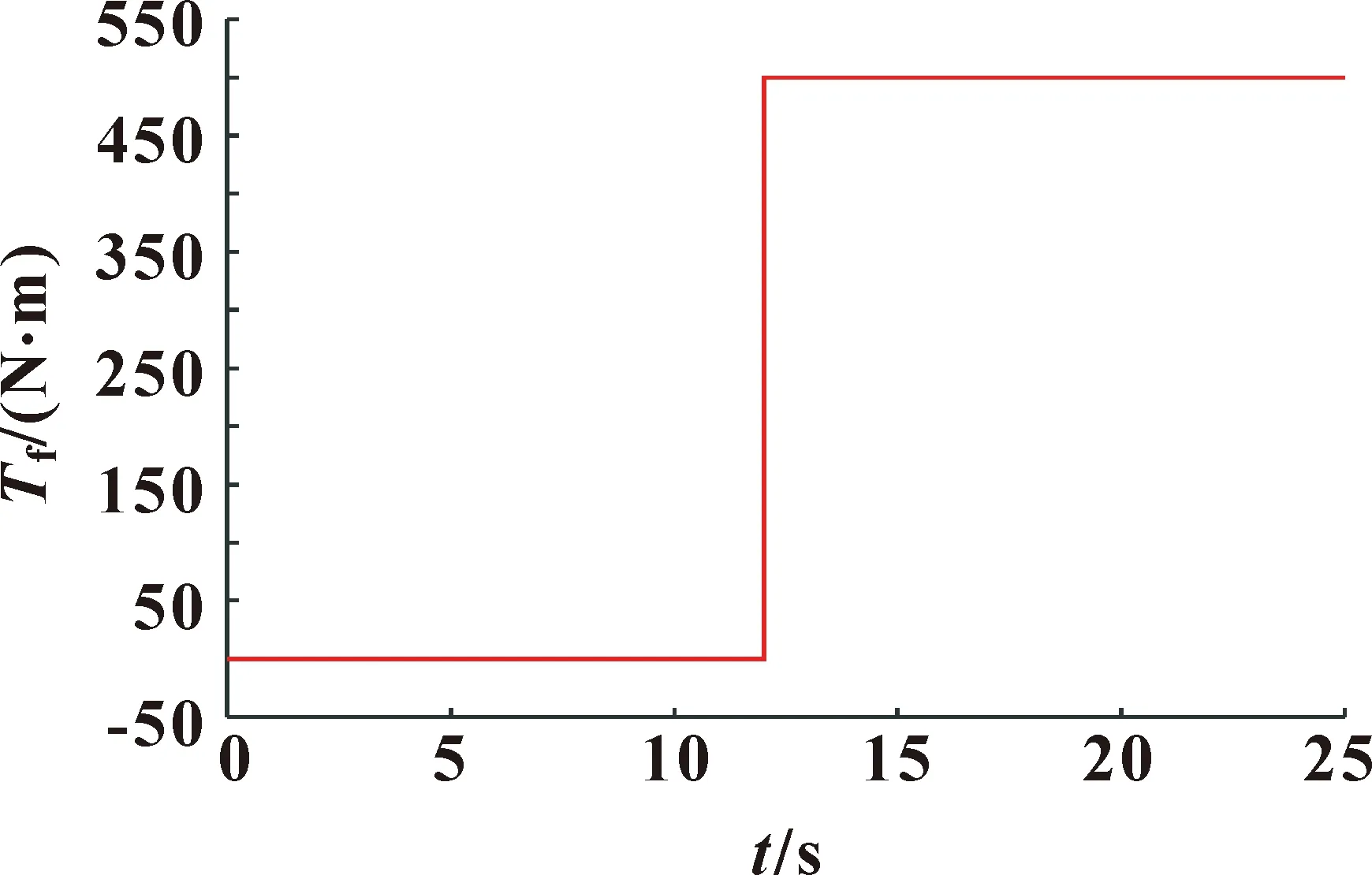
圖8 外界干擾力矩變化

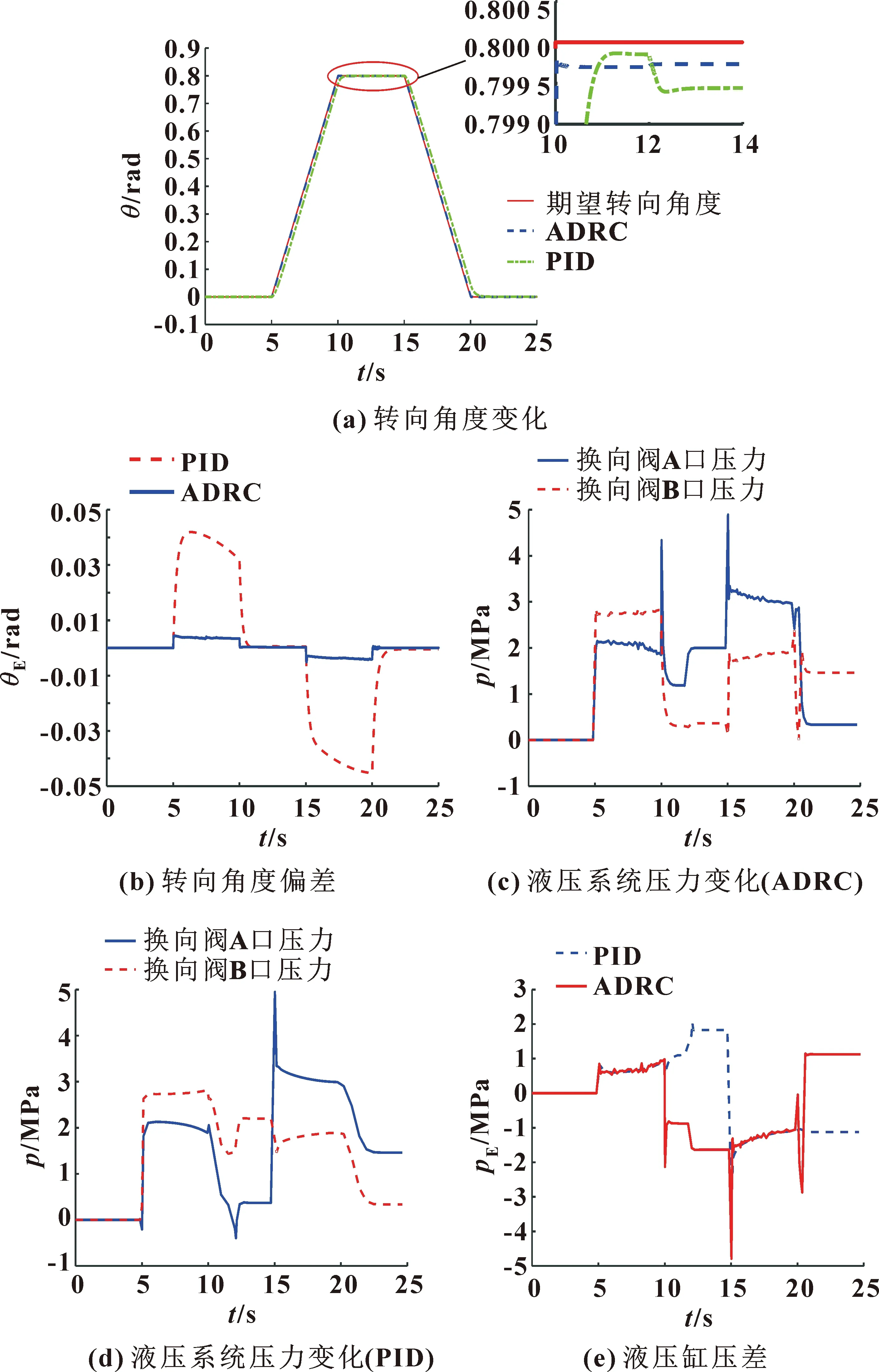
圖9 轉向控制器性能對比分析

由圖9可看出：在5～10 s和15～20 s內，鉸接車輛轉向角度均處于逐漸變化過程中。液壓轉向系統在5～10 s受轉向阻力矩的作用，在15～20 s同時受轉向阻力矩和轉向干擾力矩的作用。這兩個轉向階段中，基于ADRC控制的轉向角度實時跟蹤誤差小、跟蹤速度快。由前文知，12 s時車輛處于以最大轉向角度穩定轉向過程中，此時加入500 N·m的轉向干擾力矩后，為將車輛的實際轉向角度快速穩定在目標值，換向閥A口與B口間的壓差隨之增大，且ADRC控制下的轉向角度和液壓缸壓力以更快的速度趨于穩定。結果表明：相對于PID控制，基于ADRC控制的液壓轉向系統抗擾動性能更好，可以提高鉸接車輛的轉向穩定性和路徑跟蹤精度。

4 結語

根據鉸接車輛行駛過程中前后車體的力學特性，結合其運動學特點，基于MATLAB/Simulink建立包括非線性輪胎模型、非線性車身模型、非線性液壓轉向系統模型和ADRC控制器在內的鉸接車輛整車模型，并進行轉向運動學和動力學仿真分析。由分析可知，基于ADRC控制的液壓轉向系統可快速、穩定、無超調地跟蹤鉸接車輛的期望轉向角度，實時轉向角度誤差在0.017 rad以內，具有更好的抗擾動性能，可提高鉸接車輛的轉向穩定性和路徑跟蹤控制精度；同時注意到，液壓缸壓力在鉸接車輛轉向角度變化過程中存在波動，且在轉向角度曲率改變的瞬間，波動較明顯。這兩種現象與ADRC控制器參數的整定精度、車輪驅動力分配和液壓系統油液彈性模量等因素有關，后續將深入研究。