基于決策融合與機器學習的鐵路道岔故障診斷

張玉霞

(陜西交通職業技術學院,軌道交通學院,陜西,西安 710018)

0 引言

在鐵路運輸中,鐵路道岔故障嚴重影響了鐵路運行效率和安全,若不及時對道岔進行識別和診斷,極易出現重大交通事故。因此,對道岔健康進行實時診斷和提前預防具有重要意義。然而,傳統的鐵路道岔故障診斷依舊采用人工診斷方式,存在診斷時間長、效率低和準確率低的問題。針對此問題進行的研究有:楊菊花等[1]提出了基于CNN-GRU模型的道岔故障診斷算法研究,利用CNN網絡的深層特征學習特性,與GRU網絡相結合,很大程度上提升了道岔故障的準確率;謝博才等[2]深入探索了基于機器學習的道岔故障診斷與預測,利用機器學習中的BP神經網絡對道岔故障進行特征提取,實現了道岔故障診斷的有效性;李婉婉等[3]提出基于GMM聚類和PNN的道岔故障診斷研究,將GMM聚類與PNN進行決策融合,發揮兩者的優勢,使得故障診斷誤差減小,診斷效率和準確率提升。結合以上學者研究成果,本文提出將機器學習和決策融合技術相結合,構建基于PNN決策融合道岔故障診斷模型,通過該模型實現道岔故障準確診斷,降低安全事故發生概率。

1 PNN道岔故障診斷模型構建

概率神經網絡(PNN)是根據統計原理進行分析的前饋網絡,具備分類準確率高的優點[4],其網絡結構主要分為輸入層、模式層、求和層和輸出層等4個部分,具體結構如圖1所示。

圖1 PNN網絡結構

輸入層主要負責對樣本數據進行接收,數據維度與神經元相對應,輸入層單個神經元的輸出表示為

(1)

式(1)中,Wi表示輸入層與模式層間的連接權值,δ表示平滑因子[5]。通過式(1)可求出求和層樣本集類別的概率密度函數(PDF),其類別與求和神經元一一對應。

輸出層負責將上層的最大的概率密度進行輸出,其輸出神經元個數與上層對應[6]。

PNN故障診斷中,若故障類別表示為θA、θB,需判斷的故障樣本X=(x1,x2,…,xn)表示為

hAlAfA(X)>hBlBfB(X)

(2)

X∈θA

(3)

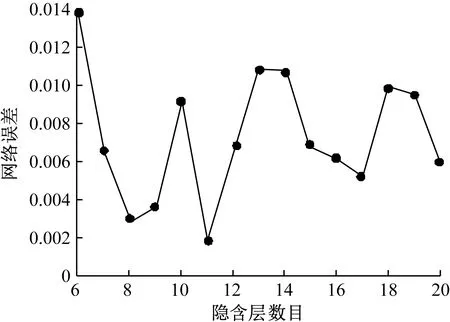
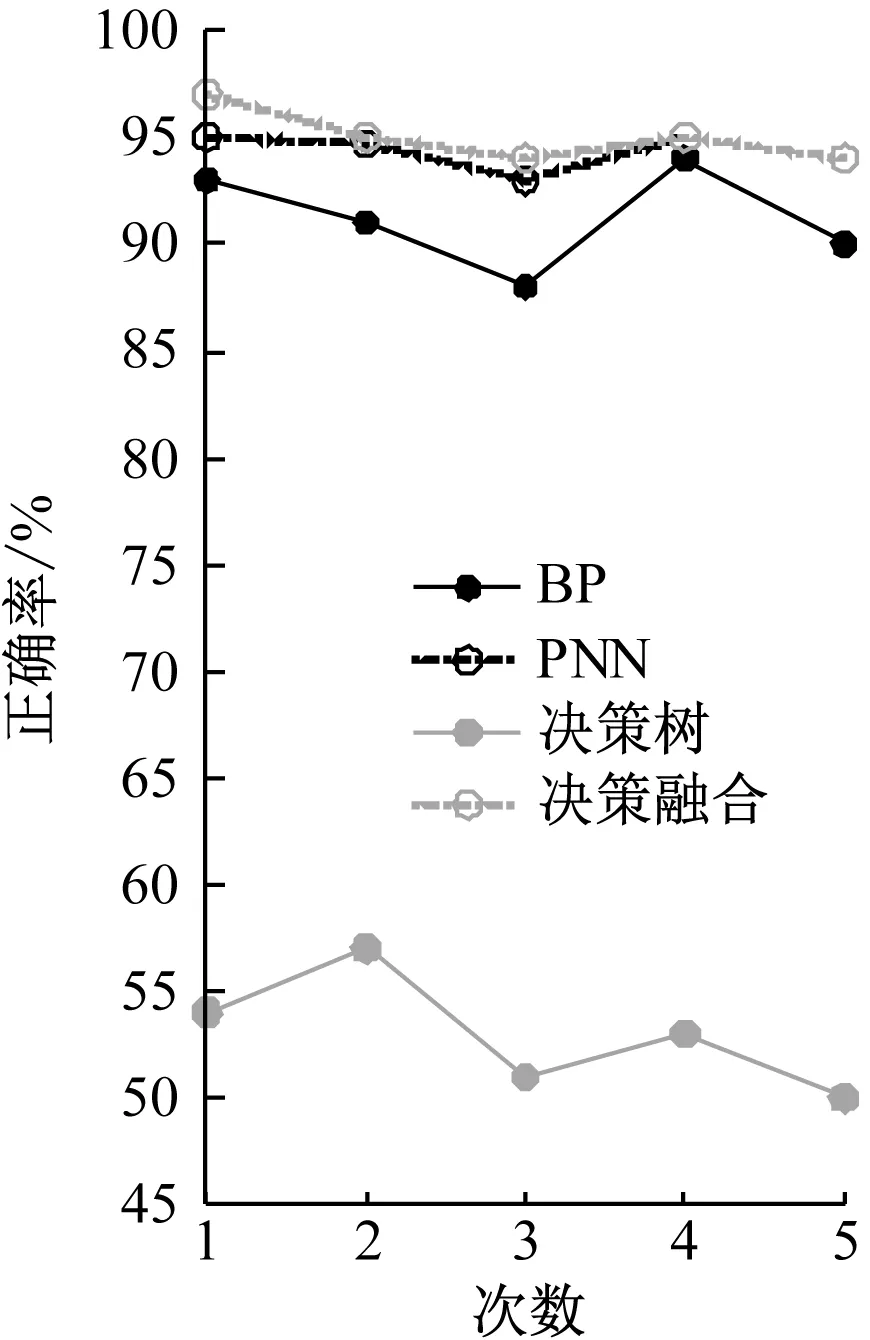
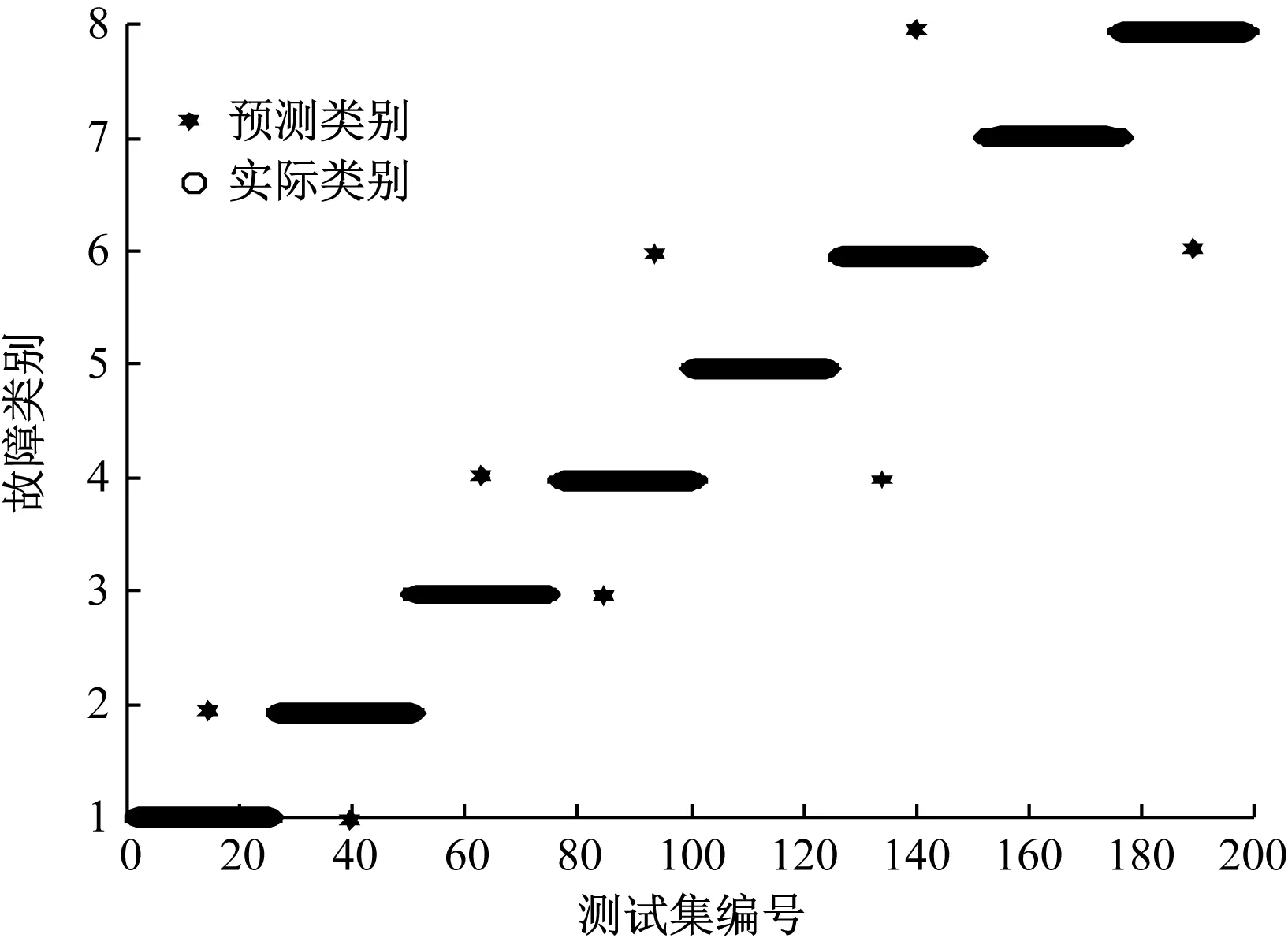
hAlAfA(X)

(4)

X∈θB

(5)

式(2)～式(5)中,hA、hB表示故障類別θA、θB的先驗概率(hA=NA/N,hB=NB/N),NA、NB分別表示故障類別θA、θB的樣本數目[7-10],N表示樣本總數,lA表示屬于θA類但劃分至θB類的代價因子,lB反之,fA、fB表示故障類別θA、θB的概率密度函數。

道岔故障診斷屬于非線性問題,通過PNN網絡能對非線性數據進行處理,因此構建基于PNN網絡的道岔故障診斷模型,見圖2。

圖2 PNN故障診斷模型

圖2中,采集訓練集數據后,即可建立平滑因子可變的PNN網絡,找出最佳平滑因子,確定參數,提升PNN網絡故障診斷正確率[11];最后建立PNN網絡,并利用測試集進行網絡測試,由此得到診斷結果。

2 基于 PNN 決策級融合的故障診斷

2.1 PNN 決策級融合故障診斷原理

為進一步提升故障診斷模型的預測能力,在結合PNN故障診斷基礎上,融合BP和決策樹的診斷模型,從而發揮決策融合技術和PNN網絡的優勢,降低錯誤判斷率。具體思路如圖3所示。

圖3 基于PNN決策級融合故障診斷模型原理

首先采集道岔樣本集;然后將樣本分別輸入至各模型中進行訓練和測試,輸出各模型的預測數據并進行歸一化處理;再利用平滑因子選出最優預測參數;最后將最優平滑因子輸入基于PNN網絡的故障診斷模型中,最終完成道岔故障診斷。

2.2 決策級融合的故障診斷模型構建

基于圖3的模型構建原理,構建基于PNN決策級融合的故障診斷模型如下。

(1) 對采集的原始數據進行預處理,獲得樣本集。

(2) 利用MATLAB構建基于BP網絡、決策樹和PNN網絡的故障診斷模型,進行比較分析后,將訓練測試完成的模型用于PNN決策級模型[12]。

(3) 將輸入層和輸出層分別設置為3個和8個神經元,且輸入和輸出分別為道岔狀態類別編號。PNN決策級融合結構如圖4所示。

圖4 PNN決策級融合結構

(4) 最后分別對基于PNN的決策級模型和初始模型在初始模型失效和模型完好的情況下進行模型性能測試,判別此模型故障診斷正確率是否得到提升。

3 實驗結果與分析

3.1 實驗環境

為了驗證構建模型的有效性,實驗開發鐵路道岔系統,軟件平臺選用Pycharm 2017,Visual Studio 2017,硬件平臺的處理器型號為Intel(R)Core i5,選擇Windows 7作為操作系統,開發語言為Python,C#。

3.2 實驗數據

為了取得更好的實驗效果,本次實驗數據來自某鐵路段監測系統對ZD6 型道岔設備采集的故障動作電流數據。正常的ZD6 型道岔動作電流如圖5所示。

圖5 正常的道岔電流

通過圖5可以看出,道岔動作電流曲線包含10個關鍵點,標記為T1～T10。根據道岔控制電路原理,圖5的電流曲線可分為3步,總共4個時間段。T1～T2表示1DQJ 吸起到道岔動作點,此時動作時間一般在0.2～0.3 s,動作電流一般在6～10 A;T2～T9 為道岔動作至鎖閉,該階段電機電流大、轉速慢,同時道岔電流通過轉換后,此時的曲線比較平滑;T9～T10為電流記錄結束區,此時電流值降為0。通過對動作電流曲線的分析,將道岔狀態分為8類,包含7種道岔故障和1種正常狀態,具體見表1。

表1 本實驗道岔故障類型

選擇t=(0.1,0.3,0.5,0.7,0.9,2.0,3.0,4.0,5.0,5.5,6.0,6.5)共12個瞬時電流值為特征信息,采集到的數據共1200條,然后按照8∶2的比例分為訓練集960條和測試集240條。由于故障樣本相對較少,所以選擇其中的720條正常樣本和480條故障樣本。在完成上述樣本數據集構建后,輸入MATLAB軟件中進行分析仿真。

3.3 參數設置

3.3.1 BP神經網絡參數

為達到最好的故障診斷效果,同時方便進行對比,設定隱含層神經元數目為14,網絡訓練的精度設定為0.001,最大訓練步長設定為2000,網絡學習的速率設定為0.1,同時采用均方誤差作為評價函數。在以上基礎數據下,比較不同訓練函數和最佳隱藏層節點對訓練結果的影響,具體結果見表2和圖6。通過表2看出,選擇trainlm訓練函數得到的均方誤差最小,且當隱含層數為11時網絡訓練誤差最小。

表2 不同訓練函數下的預測均方誤差

圖6 不同隱含層數下的網絡訓練誤差

綜上,BP神經網絡的訓練函數選擇trainlm,隱藏層節點數設定為11。

3.3.2 PNN參數設置

結合PNN網絡結構,將輸入層維度設定為12,輸出層維度為8,同時采用試湊法對PNN平滑因子進行優化,具體結果如圖7所示。

圖7 不同平滑因子對分類正確率的影響

通過圖7得出,當 SPREAD 為 0.5 時,模型正確率超過 95%,因此選其作為最優平滑因子進行最終網絡測試。

3.3.3 決策樹參數

決策樹的參數設定為max_depth=15,max_features=0.999,min_sampe_leaf=1.0,min_sample_split=25。

3.4 評價指標

選用準確率(P)、漏報率(MA)和虛警率(FA)作為故障診斷結果評價指標,具體計算式為

(6)

(7)

(8)

式(6)～式(8)中,TP、TN、FP、FN分別表示真正例、真反例、假正例和假反例。

3.5 基于PNN決策級融合故障診斷模型驗證

完成以上單一診斷模型測試后,對基于PNN決策級融合的故障診斷模型進行驗證和分析。分別在某一模型失效和模型完整兩種情況下進行驗證,通過2種方式測試決策級模型是否具備容錯性以及模型正確率是否得到提升。

3.5.1 某一模型失效情況下驗證與分析

(1) BP網絡失效或PNN網絡失效

將測試集的數據應用到基于PNN決策級融合的故障診斷模型中進行測試,當模型正確率低于60%時,說明此模型失效。對模型參數進行優化后,得到最終輸出的正確率模擬模型失效情況,如圖8、表3、表4所示。

表3 BP網絡失效正確率統計表 單位:%

表4 PNN網絡失效正確率統計表 單位:%

由圖8、表3、表4可知,在BP模型或PNN模型失效情況下,決策級融合模型的預測正確率均保持在92%以上,預測效果較好,沒有發生明顯變化,說明決策級融合模型具有較高的容錯性。

(2) 決策樹失效或BP和決策樹網絡失效

利用測試集進行測試,結果如圖9、表5和表6所示。

表5 決策樹失效情況下正確率統計表 單位:%

表6 BP和決策樹網絡失效情況下正確率統計表 單位:%

圖9 決策樹失效或BP和決策樹網絡失效情況下的關系圖

從圖9、表5、表6可知:在決策樹失效情況下,決策級融合的預測準確率高達98.7%,均保持在94%以上;而在BP和決策樹網絡失效情況下,決策級融合的預測準確率依舊在91%以上。由此說明,決策樹失效或BP和決策樹網絡失效對決策級融合的影響較小,該模型具備容錯性。

3.4.2 初始模型完好情況下的驗證與分析

在3種初始模型完好的情況下,通過5次不同測試集對決策級模型進行測試,測試結果如圖10、表7所示。

表7 初始模型完好情況下正確率統計表 單位:%

圖10 初始模型完好情況下正確率

由圖10、表7可知,在3種初始模型完好狀況下,決策級融合模型的預測效果依舊高于3種初始模型,且該模型的診斷正確率均在95%以上,高達98.1%,說明此模型的正確率得到提升。

完成準確率是否提升的測試后,利用測試集對PNN決策級模型進行測試,得到實際類別與預測類別的結果,如圖11、圖12所示。

圖11 PNN決策級融合模型實際圖與預測圖

圖12 PNN決策級融合模型各類別正確率統計圖

從圖11、圖12可以看出,PNN決策級融合模型的正確率為98%,明顯高于另外3種模型,漏報率和虛警率僅為3%,由此說明決策級融合模型的正確率得到提升,誤判率和漏判率下降,對道岔故障診斷具有較好的識別和分類效果。

4 總結

綜上,構建的基于PNN決策級融合故障診斷模型具備可行性和有效性,故障診斷的正確性進一步提升,并具有一定的容錯性,模型性能優越。實驗結果表明,在單一模型失效情況下,決策級融合模型依舊可以保持較高的準確率。同時,對比完好狀況下的模型,決策級融合模型的診斷正確率高達98.1%,比BP網絡、PNN模型和決策樹提升了6.3%、4.5%和9.6%,模型預測能力顯著提升。