P-RSHMU蒸發波導預測與湍流通量相關性分析

張利軍，張超，王紅光，郭相明，韓杰，張守寶

（中國電波傳播研究所，山東青島 266107）

0 引言

近海面水汽會隨著高度迅速下降而形成蒸發波導，該類型大氣波導發生概率高，因此受到雷達以及電波傳播學界的極大關注。這種反常的傳播環境會極大地影響海洋環境中的雷達、通信、電子對抗設備的性能，尤其會使得雷達實現超視距傳播或者形成雷達盲區等。從20 世紀60 年代開始，伴隨著微氣象學的發展，國內外的科研工作者基于海上氣象觀測數據，以相似理論為基礎開始了蒸發波導模型的研究分析，相繼提出了JESKES 模型[1]、ROTHERAM 模 型[2]、FAIRALL 模 型[3]、PAULUSJESKES 模型[4]、RSHMU（Russian State Hydrometeorological University，俄羅斯國立水文氣象大學）模型[5]、MGB（Musson-Gauthier-Bruth）模 型[6]、BYC（Babin-Young-Carton）模 型[7]、NPS（Navy Postgraduate School，海軍研究生院）模型[8]以及偽折射率模型[9]等。

RSHMU 模型公開發表時間較晚，針對此模型的適用性分析文獻較少。由于文獻[5]中的溫度濕度剖面穩定度函數存在編輯錯誤，導致張永剛等[10-11]在錯誤地引用了這些剖面穩定度函數后，得到RSHMU 模型預測風速特征參數的結果較差以及溫度、濕度剖面函數在南海海區不適用的結論。張利軍等[12]更正了溫度、濕度剖面穩定度函數的編輯錯誤，并基于正確的剖面穩定度函數給出了該模型在不穩定條件下的高度預測，結果優于美國NPS 模型。進一步地，張利軍等[13]借鑒了PAULUSJESKES 的訂正方法，給出了改進的RSHMU 模型（即P-RSHMU 模型），該模型在不穩定條件下的預測性能保持不變，穩定條件下的預測性能獲得極大提高，因此基于P-RSHMU 蒸發波導模型，能夠給出適合穩定條件以及不穩定條件下的合理蒸發波導高度。

郭相明等[14]基于海上梯度塔觀測數據，分析了多種蒸發波導預測模型的適用性。郭相明等[15]還應用湍流通量分析了蒸發波導的形成機理，并利用TOGA-COARE 實驗期間測試的1992 年11 月25—26 日的一組不穩定大氣時的實驗數據，定性分析了蒸發波導的生成和變化與代表湍流運動的湍流通量的關系。眾所周知，海氣界面通量交換是海氣相互作用的重要環節，海氣界面通量的確定在海氣相互作用研究方面具有重要意義，受到海洋學界和氣象學界的廣泛重視。張超等[16]從基本的氣象觀測資料出發，利用經海上觀測數據驗證有效的耦合海洋-大氣響應試驗（Coupled Ocean-Atmosphere Response Experiment，COARE）通量算法[17-18]以及改進的NPS蒸發波導預測模型，計算獲得了南海北部海域海面湍流通量以及蒸發波導高度，并定量分析了二者之間的相關性。由于穩定條件下低風速時改進的NPS 模型計算可能出現蒸發波導高度達40 m 的情形，進而可能影響穩定條件下蒸發波導高度與湍流通量的相關性計算，因此本文引入預測精度較高的P-RSHMU 蒸發波導模型，基于海上氣象水文數據計算蒸發波導高度，有效抑制了穩定條件下蒸發波導高度預測不合理的現象。進一步地，討論了PRSHMU 模型預測高度與張超等[16]給出的湍流通量結果的相關性。這些結果可為深入理解蒸發波導的形成機理和內涵提供參考。

1 湍流通量、蒸發波導高度計算方法

1.1 湍流通量計算方法

海氣界面通量的計算方法通常分為直接計算方法和整體參數化（Bulk Parameter）方法。直接計算方法是根據通量的定義直接測量氣象要素的湍流脈動量并計算其二階矩，該方法是相對最準確的方法，但由于實際中會受到人力、物力以及觀測手段的影響，因此通常采用整體參數化方法來估計海氣界面的湍流通量[17]。整體參數化方法依賴于風速、溫度、濕度等基本氣象參數，目前普遍使用的是計算湍流通量的整體公式，較為先進且普遍認可的通量算法是COARE 算法，該算法可以計算風速、溫度、比濕的特征參數，進而計算海氣湍流通量。海氣湍流通量關系式定義如下[18]：

式中：M為動量通量，單位：N/m2；HS為感熱通量，又稱顯熱通量，單位：W/m2；HE為潛熱通量，單位：W/m2；ρ為空氣密度，單位：kg/m3；cp為空氣定壓熱容，單位：m2/（s2·K）；LE是水的蒸發潛熱，單位：J/kg；w'、u'、θ'、q'分別表示垂直風速、水平風速、位溫、比濕的湍流脈動值；u*、θ*、q*分別為莫寧奧布霍夫相似（Monin-Obukhov Similarity，MOS）理論中的風速、位溫、比濕特征量。

1.2 P-RSHMU蒸發波導高度計算方法

蒸發波導高度采用P-RSHMU 模型[13]計算。近地層的溫度剖面以及比濕剖面計算公式如下[19]：

式中：Tsea、qs分別為海表溫度（單位：K）以及海面比濕（單位：kg/kg）；θ*、q*分別為位溫特征量、比濕特征量；κ為卡曼常數，取0.4；z0θ、z0q分別為溫度粗糙度和比濕粗糙度分別為溫度普適函數和比濕普適函數；Γd為干絕熱遞率，取0.009 76 K/m；z為高度，單位：m。

需要特別指出的是，溫度和濕度剖面穩定度函數的正確表達式為[12]：

式中：β1= 8；y1=(1 -β2ξ)13；β2= 35；γ2= 6。

大氣壓力剖面由流體靜力學公式以及理想氣體定律聯合確定，積分得到如下壓力剖面公式[19]：

式中：R為干空氣理想氣體率常數287.04 J/（kg·K）；為層高度z1和z2處平均虛位溫。

由比濕以及壓力剖面計算水汽壓e剖面[19]：

式中：ε為干空氣氣體常數以及水汽常數之比，取0.621 7）。一旦確定了溫度、水汽壓、壓強剖面，修正折射率[19]剖面可以按照下式計算得到：

通過尋找M 剖面中的最小值即可確定對應的蒸發波導高度。進一步地，當氣海溫差小于-1 ℃時，采用RSHMU 模型計算方法；當氣海溫差大于-1 ℃時，保持海溫不變，利用RSHMU 模型分別計算氣海溫差等于-1 ℃以及等于0 ℃的蒸發波導高度h-1和h0，如果h0>h-1，則蒸發波導高度為h-1，否則依照原來的氣溫與海溫來計算蒸發波導高度[13]。該方法即為蒸發波導P-RSHMU模型的計算方法。

2 數據資料與計算結果

2.1 數據資料

依托廣東茂名博賀海洋氣象科學試驗基地的海上試驗平臺[20]，采用要素集成的氣象傳感器以及海溫傳感器，以分鐘級為單位，采集了2017 年11 月26 日—2018 年5 月31 日的氣象數據，包含氣溫、海溫、相對濕度、氣壓、風速、風向、降雨量等數據，共計262 769 組。剔除湍動分量的影響，對分鐘級的氣象要素進行小時平均，獲得小時的氣象要素分布，共計4 395組。

基于P-RSHMU 模型計算獲得小時蒸發波導高度，結果見圖1。由圖可見，大部分蒸發波導高度位于0～20 m，沒有出現蒸發波導高度為40 m的現象，波導高度曲線呈現連續變化。而張超等[16]基于改進的NPS模型計算出的蒸發波導高度在5月中下旬風向穩定的時段，可能出現極其穩定的條件，此時蒸發波導高度為40 m，且呈現跳躍變化。為對比起見，圖2 給出該模型計算結果與改進的NPS 模型的結果對比圖，由圖可見，大部分情形下二者一致性較好，P-RSHMU 模型有效抑制了蒸發波導高度較高尤其預測的蒸發波導高度為40 m的情形。

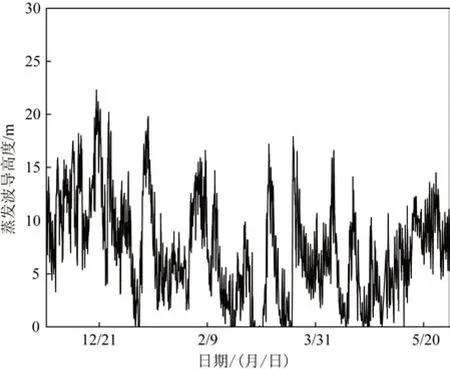
圖1 蒸發波導高度計算結果Fig.1 Calculation result of evaporation duct height

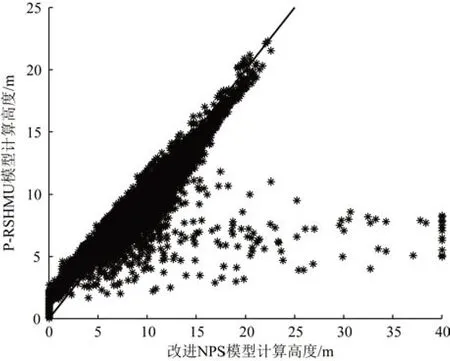
圖2 不同模型計算結果對比Fig.2 Comparison of calculation result between different models

2.2 相關性分析

將計算的蒸發波導高度與潛熱通量、感熱通量、動量通量作散點圖，由圖3 可見，蒸發波導高度與潛熱通量以及動量通量呈現某種線性關系，而與感熱通量的線性關系不明顯。進一步地，計算蒸發波導高度與潛熱通量、感熱通量、動量通量的相關系數分別為0.92、-0.12、-0.41。

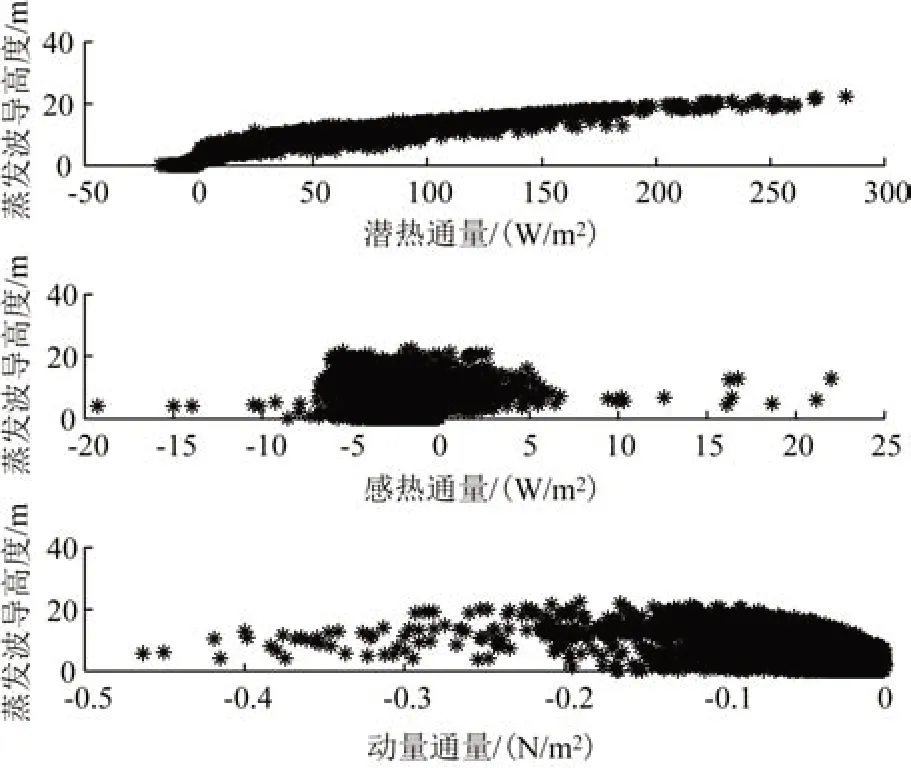
圖3 湍流通量與蒸發波導高度散點圖Fig.3 Scatter plot of turbulent flux and evaporation duct height

以大氣溫度與海水溫度之差為標準區分穩定條件，并分別給出不穩定條件（氣海溫差＜0 ℃）、中性條件（氣海溫差=0 ℃）、穩定條件（氣海溫差＞0 ℃）下的蒸發波導高度與湍流通量的散點圖，結果如圖4—6。不穩定條件（見圖4）以及中性條件下（見圖5）的散點圖與張超等[16]研究結果類似，而穩定條件下（見圖6）的散點圖顯著不同于文獻[16]，圖7給出了穩定條件下文獻[16]的散點圖進行對比。

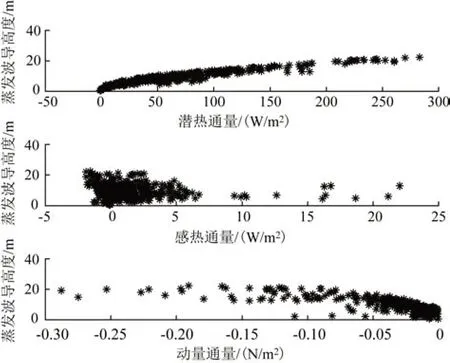
圖4 不穩定條件下湍流通量與蒸發波導高度散點圖Fig.4 Scatter plot of turbulent flux and evaporation duct height under unstable condition

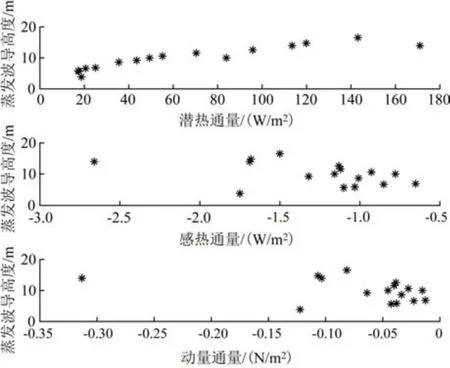
圖5 中性條件下湍流通量與蒸發波導高度散點圖Fig.5 Scatter plot of turbulent flux and evaporation duct height under neutral condition

圖6 穩定條件下湍流通量與蒸發波導高度散點圖Fig.6 Scatter plot of turbulent flux and evaporation duct height under stable condition

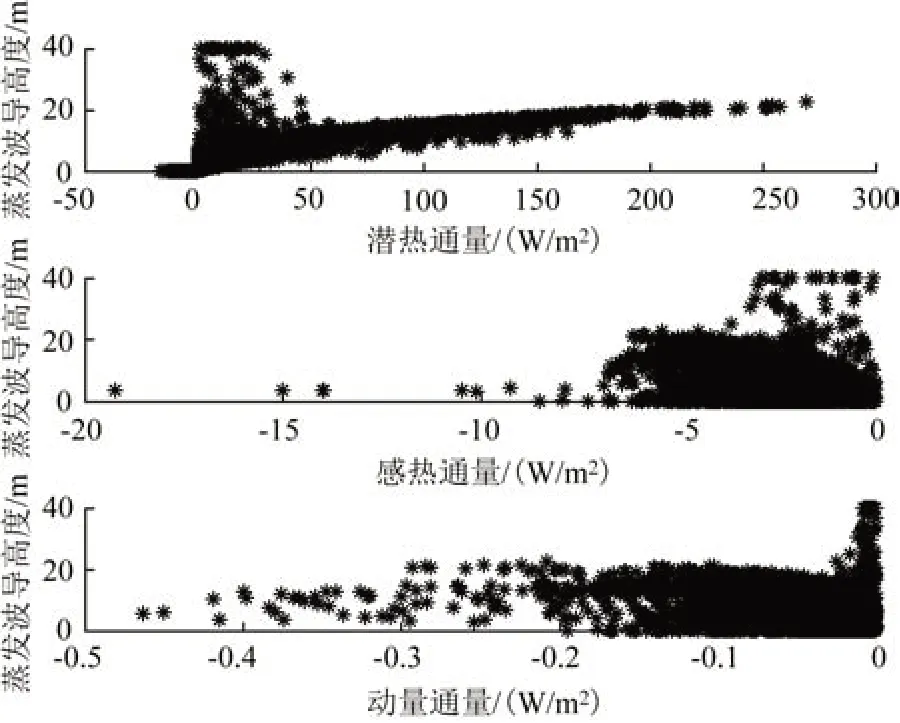
圖7 穩定條件下的計算結果（引自文獻[16]）Fig.7 Calculation result under stable condition(cited from literature[16])

張超等[16]指出，40 m 的蒸發波導高度存在于0 N/m2動量通量、-3～0 W/m2感熱通量以及0～40 W/m2潛熱通量附近。動量通量較小，對應風速較小，感熱通量為負，對應感熱由上面的大氣向下面的海洋傳輸能量，即氣海溫差＞0 ℃，因此在穩定條件下，較低的風速導致蒸發波導高度的預測效果較差。這可能與該條件下湍流輸運不夠旺盛進而導致蒸發波導預測理論MOS 中假定近海面空間為常通量不成立有關。

文中引入的P-RSHMU 模型則有效地避免了穩定條件下預測蒸發波導高度不合理的現象，在穩定條件下同樣可以獲得與不穩定條件、中性條件一致的預測結果。區分不同穩定性條件下蒸發波導高度與湍流通量的相關系數見表1，其中穩定條件計算樣本數為3 969，中性條件為16，不穩定條件為410。由表中數據可以看到，在不區分穩定性條件下，潛熱通量與蒸發波導的高度最相關，動量通量次之；不穩定條件下，兩者具有一致的相關性特征；中性條件下，感熱通量的相關性次之；穩定條件下，動量通量的相關性次之。整體來說，潛熱通量對應著水汽相變直接影響蒸發波導的生成，動量通量又或快或慢地影響海面水汽蒸發進而間接影響蒸發波導的生成，感熱通量僅僅代表由于溫度差異導致海洋向大氣或者大氣向海洋輸送的熱量，對整體的湍流通量貢獻較小，因此潛熱通量、動量通量與蒸發波導高度的相關系數大于感熱通量。

2.3 對比分析

作為對比，表1還列出了文獻[16]的相關系數結果。由表中數據可以看到，引入的P-RSHMU 模型顯著改變了穩定條件下即氣海溫差＞0 ℃時湍流通量與P-RSHMU 蒸發波導高度的相關系數，計算結果較為合理。

需要特別指出的是，穩定條件下改進的NPS 模型在氣海溫差＞0 ℃時以及動量通量較小（或者風速較小）時會出現蒸發波導高度為40 m 或者計算波導高度偏高的現象，導致該條件下計算的蒸發波導高度與潛熱通量的相關系數為0.73，而P-RSHMU模型則抑制了這種現象的出現，進而二者的相關系數提高到0.92，且保持了與不穩定條件以及中性條件一致的計算結果，即蒸發波導與潛熱通量顯著相關。

通常情況下蒸發波導被認為是由于近海面水汽蒸發從而引起大氣濕度隨高度銳減而形成的一種大氣層結。近海面水汽可認為是飽和的，隨著高度的增加，相對濕度迅速下降進而形成蒸發波導。而潛熱通量是由于水汽相變向大氣傳輸的熱量通量，因而文中計算的蒸發波導高度與潛熱通量的相關系數為0.92，有力支撐了蒸發波導的形成原因。

3 結論

本文基于海上平臺觀測的水文氣象數據，利用不同穩定性條件下預測效果都較好的P-RSHMU 模型，計算獲得不同時刻的蒸發波導高度，有效抑制了穩定條件下蒸發波導預測高度為40 m 或者預測偏高的不合理現象。進一步地，分析了該模型預測蒸發波導高度與動量通量、感熱通量、潛熱通量等湍流通量參數的相關性，結果表明蒸發波導高度與潛熱通量高度顯著相關，相關系數可達0.92，與動量通量相關性次之，相關系數為-0.41，與感熱通量的相關系數最小，為-0.12。這些結果進一步為豐富蒸發波導的內涵以及形成機理提供重要數據支撐。