一種基于集成機器學習的液態金屬電池快速分選方法

夏珺羿 石瓊林 蔣 凱 何亞玲 王康麗

（1.強電磁工程與新技術國家重點實驗室（華中科技大學電氣與電子工程學院） 武漢 430074 2.電力安全與高效利用教育部工程研究中心 武漢 430074）

0 引言

隨著國家“碳達峰、碳中和”目標的提出，適應大規模高比例新能源成為電力系統的未來發展趨勢。然而以太陽能和風能為代表的可再生能源具有較強的波動性與間歇性，大規模并網會對電力系統的穩定性構成巨大的挑戰，而儲能技術有望解決這一難題。在各種儲能技術當中，電化學儲能能量密度大、能量效率高、響應速度快、配置靈活，是規模儲能技術發展的重要方向[1-3]。

在諸多電化學儲能技術中，液態金屬電池（Liquid Metal Battery, LMB）是一種面向電網規模儲能的新型電池儲能技術，具有長壽命、低成本等明顯應用優勢[4-9]。據報道，2020 年12 月，TerraScale公司計劃為位于內華達州的Energos Reno 數據中心項目部署可再生能源發電設施和儲能系統，將采用規模為250 MW·h 的液態金屬電池儲能系統。近年來，電化學儲能電站的規模呈現集中式、大型化的發展趨勢。MW·h 甚至GW·h 級別的儲能系統涉及海量的電池成組運行[10-11]。系統性能與電池單體的狀態參數密切相關，成組電池間的不一致性不僅會顯著降低儲能系統性能，還可能會引起安全隱患。為了實現液態金屬電池在儲能系統中的應用，需要通過電池分選方法篩選出一致性較好的電池進行成組使用。電池分選是指通過容量、內阻等關鍵分選指標對電池進行篩選、分類并重組，是降低成組電池間不一致性，提升儲能系統性能的有效手段。

電池分選方法包括兩個重要的組成部分：分選指標的獲取與分類重組方法。與分選指標的客觀性相比，分類重組方法的標準更具主觀性并與應用場景密切相關。此外，分類重組方法結果在很大程度上取決于所獲得的分選指標的精度。因此，電池分選指標的獲取在電池分選中處于中心位置。傳統的通過電池標定獲取電池分選指標的方法雖然能實現對分選指標零誤差的測量，但是會耗費大量的測試時間與成本，難以適用于規模化儲能系統的電池分選。基于機器學習的分選方法具有快速、準確等優點，更適合海量電池的分選。

目前，電池分選的研究主要聚焦于鋰離子電池，特別是退役鋰離子電池的重組利用，而關于液態金屬電池分選的研究極為缺乏。對于分選指標的獲取，現有方法一般以獲取的電壓、電流等關鍵特征參數作為輸入，以容量或內阻等需要預測的分選指標作為輸出，通過數據訓練構建輸入輸出的映射，所得到的映射一般也被稱為機器學習模型。機器學習模型所需要的輸入特征通常需通過額外的電池測試獲取。例如，文獻[12-15]利用電池充電曲線獲取預測用特征，文獻[16]通過阻抗譜測試提取特征，文獻[17]將電池放電測試中特定時間點的三個電壓值作為特征。目前常用的機器學習模型為支持向量機[12]、高斯過程[15]、相關向量機[14]和神經網絡[13,16-17]等，其中神經網絡是主流的模型。現有的機器學習模型對分選指標的預測誤差一般在1%～4%之間。對于電池的分類重組，現有分選方法一般利用電池容量、內阻在內的多維特征對電池間的相似程度進行衡量，通過特定算法對多個電池進行重組與分選[18-23]。目前主要的分類重組算法為各種聚類算法，包括SOM（self-organizing map）聚類[18-20]、K-means 聚類[22]、模糊C 均值聚類[21]和高斯混合模型[23]等。現階段對于分選重組后電池間不一致性的衡量尚無固定標準，但在分選重組后，電池間放電曲線的差異得到顯著減小。

然而，現有的鋰離子電池分選方法難以直接運用于液態金屬電池的成組分選。一方面，目前的分選方法主要聚焦于退役鋰離子電池分選，電池間的不一致性差距顯著，而新制備的液態金屬電池單體間的不一致性相對較小，對分選指標的估計精度要求更高；另一方面，液態金屬電池具有容量大、內阻小的特點[24]，要求分選指標的估計有更小的相對誤差。此外，現有方法獲取輸入特征需要額外的電池測試，測試時間與成本還有進一步優化的空間。

針對上述問題，本文提出了一種基于集成機器學習的液態金屬電池分選方法。與現有方法相比，在數據來源上，利用活化期的數據作為輸入，無需額外的電池測試，分選速度更快；在模型算法上，利用特征選擇和集成學習方法，所獲得的特征更有效，集成模型對分選指標電池容量的預測誤差更小且更可靠。該方法主要分為四個步驟，如圖1 所示：首先對電池數據進行整理、選擇與劃分；然后獲得基礎模型的最優超參數；接著在訓練得到集成模型之后，在測試集上驗證得到最優模型；最后基于最優模型進行電池分選。

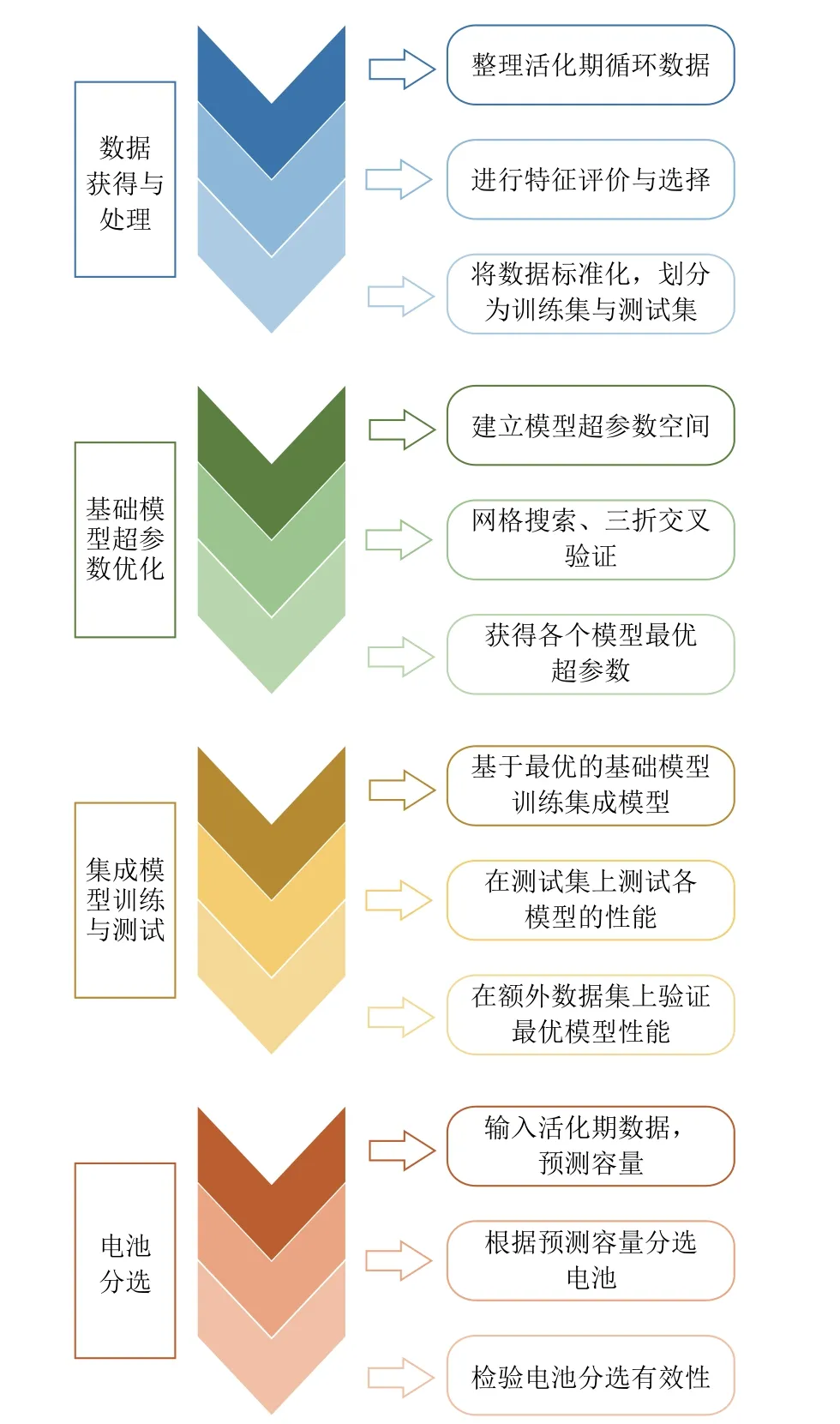
圖1 分選方法的主要工作流程Fig.1 Main workflow of proposed sorting method

本文首先介紹了液態金屬電池及其數據集，以及集成模型所用到的基礎模型和集成方法；再次，闡述了本文要解決的機器學習問題與評價指標；然后，介紹了主要工作，包括特征選擇、模型構建與優化、模型測試與驗證、電池分選四個部分；最后，根據模型的測試驗證結果和分選結果，對特征選擇方法和集成模型的優越性進行了評價與總結。

1 液態金屬電池簡介與電池數據集

1.1 液態金屬電池簡介

液態金屬電池是一類新型儲能電池，在300～700℃的工作溫度下，電池正負極和電解質分別為液態金屬和熔融態無機鹽，三者互不相溶，會根據密度差自動分層[25-26]。全液態設計使該電池在長期運行時不會出現電極形變和枝晶生長等現象，具有長壽命的顯著優勢。液態金屬電池的電極和電解質材料來源廣泛、價格低廉、無需隔膜、結構簡單、電池成本較低[27-28]。低成本、長壽命的特性讓液態金屬電池有望滿足未來電網大規模儲能的應用需求[29]。

本文采用的液態金屬電池為理論容量為50 A·h的Li||Sb-Sn 電池，其結構示意圖[30]如圖2 所示，基本參數見表1。

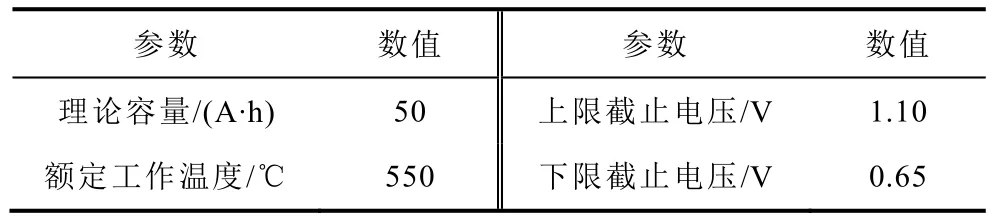
表1 Li||Sb-Sn 液態金屬電池基本參數Tab.1 Parameters of liquid metal battery

圖2 Li||Sb-Sn 液態金屬電池結構示意圖[30]Fig.2 Structure of Li||Sb-Sn liquid metal battery[30]

1.2 電池數據集與特征

本文所使用的電池數據來自50 A·h Li||Sb-Sn 液態金屬電池活化期的循環數據，共包括21 個電池的416 個循環。電池的活化期和穩定狀態的定義如下：活化為從新電池到穩定運行的過程，一般在20 個循環內電池即可到達穩定狀態，因此本文選取前20 個循環作為活化期；穩定狀態為經過活化期后再循環10 圈后的電池狀態。在活化期，電池以0.1C倍率進行充放電循環，放電容量為25 A·h。在活化循環測試中，每10 s 對電池的電壓、電流等信息進行一次采樣，每一個采樣點即為一個時間步。需要指出的是，電池在活化期循環時放電深度（Depth of Discharge, DOD）設定為50%，防止電池出現過充、過放和短路等故障。

本文將電池活化期的各個循環放電過程中的相關特征作為一個樣本，其標簽為循環所屬的電池穩定狀態的滿放容量。該數據集共有7 個特征：放電起始電壓、放電中壓、放電終止電壓、庫倫效率、直流內阻、歐姆內阻和平臺到達時間段。其中放電起始電壓、放電中壓、放電終止電壓和庫倫效率均可直接測得。歐姆內阻和直流內阻可通過放電結束后瞬間的電壓變化和靜置后的恢復電壓（如圖3 所示）計算得到，其計算公式分別為

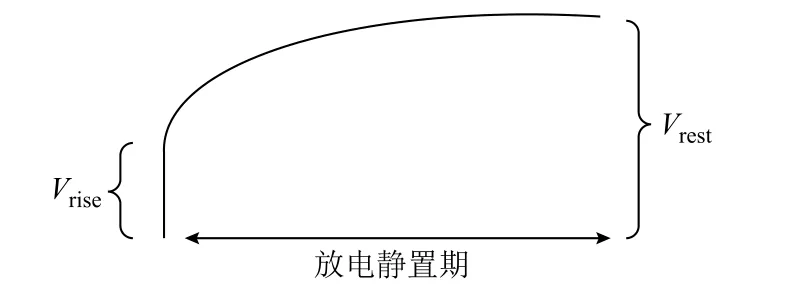
圖3 內阻計算示意圖Fig.3 Internal resistance calculation diagram

式中，Rohm為歐姆內阻；Rdc為直流內阻；Idischarge為電池放電階段的電流；Vrise為放電結束后進入靜置階段電壓的瞬時值；Vrest為靜置期電壓達到穩定的穩定值。

放電平臺的定義來自放電電壓曲線各點的切線斜率，當斜率小于某一閾值（接近于0）時可以認為放電進入平臺期。平臺到達時間示意圖如圖4 所示，本文認為電池放電電壓在10 s 內的變化小于或等于0.002 V 時電池即進入放電平臺期，這和液態金屬電池的放電特性密切相關。

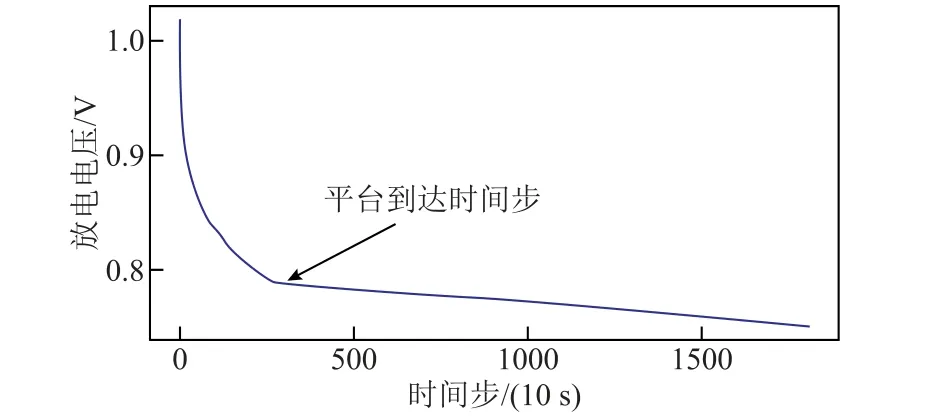
圖4 平臺到達時間示意圖Fig.4 Plateau arrival time diagram

如圖4 所示為液態金屬電池放電曲線，箭頭指示處的時間步即為平臺到達時間步。將時間軸劃分為若干個區間并對區間依次編號，平臺到達時間步所在的區間即為特征平臺到達時間段，其取值即為區間的編號。該特征能夠反映電壓曲線的部分形貌特征，從而有利于容量預測。

基于分層抽樣的方法，數據集被劃分為訓練集和測試集。其中測試集樣本數量為84，訓練集樣本數量為332。

2 所用模型與集成方法簡介

本文集成模型所用的基礎模型總共有三個，分別為支持向量回歸（Support Vector Regression,SVR）[31-32]、極端梯度提升（Extreme Gradient Boosting, XGBoost）回歸[33]和隨機森林回歸[34]；所采用的集成方法有兩種，分別為投票法和堆疊法[35]。

2.1 支持向量回歸

支持向量回歸是一種使用廣泛的機器學習模型。對于n個m維數據xi，支持向量回歸的目標是找到一個函數fsvr(xi)，對于所有訓練數據的fsvr(xi)與實際目標yi的最大偏差為ε。其函數表達式為

式中，wsvr為與x相乘的權重系數向量；b為偏置量。

實際應用中，常常允許有一定的誤差以提升模型的泛化性能，因此在優化問題中引入了兩個松弛變量ξ和ξ*，以及正則化系數C。在此條件下的優化問題為

對于非線性的回歸問題，支持向量回歸存在一種“核技巧”，即通過某種映射Φsvr將樣本映射到一個更高維的特征空間中，將樣本空間中的非線性問題轉換為高維空間中的線性問題。這種映射通常用核函數來隱式表示為

通過核函數，特征空間內的點積計算就轉換為原空間內核函數的計算。常見的核函數有高斯核、多項式核等。本文采用普適性更加廣泛的高斯核函數。

2.2 極端梯度提升回歸

XGBoost 是一種梯度提升樹的變體，其特點是運行速度極快、可擴展與可移植。

對于n個m維數據xi，該算法建立K個回歸樹來擬合實際目標yi。擬合表達式為

式中，Φboost為極端梯度提升模型中xi到yi的映射；每一個fboost-k都代表一個獨立的樹結構。

損失函數為

式中，l為一個可微的凸損失函數；T為決策樹中葉節點的數量；Ω為一個懲罰項，以避免過擬合；wboost為每棵樹中末端葉上的權重分數；γ和λ均為正則化參數。

該算法是一種貪心算法，訓練過程中在添加第t-1 棵樹后，通過添加最優的第t棵使得損失最小，即

最后根據最優損失計算得到第t個樹的最優劃分和權重。該過程會一直持續下去直到所有的K個樹都建立完畢，最終得到完整的模型。

2.3 隨機森林回歸

隨機森林是最常見的決策樹集成模型之一。隨機森林回歸算法會生成一系列不同的回歸決策樹形成一個“森林”。具體模型算法如下：

1）利用bagging 采樣方法獲得d個訓練集子集。

2）在每個子集上分別訓練一個回歸決策樹。

3）訓練時，每個決策樹分裂時不是采用所有特征，而是用隨機的特征子集來劃分數據。特征子集的最大數量是固定的，但所含特征是隨機選擇的。在分裂時從子集中選擇一個最優特征，然后找到最優劃分點。

4）隨機森林回歸模型預測的結果是所有d個決策樹模型的預測結果的平均值。

2.4 集成方法

將一組預測模型的預測聚合起來就稱為集成。集成方法能夠將較弱的模型集合成一個更強的模型，集成得到的模型性能與泛化能力一般強于用于集成的基礎模型。在諸多集成方法中，投票法和堆疊法適用于集成多個完全獨立的基礎模型，所以本文采用這兩種方法作為集成的備選方法。

對于回歸問題來說，投票法就是將e個基礎模型單獨訓練，然后將它們的預測結果進行平均。投票法能夠提升模型整體性能的原理是，不同的模型所犯的錯誤的類型不同，將不同模型的預測結果進行平均能夠減少整體的誤差，其表達式為

式中，Pi為對樣本xi的最終預測結果；Pe-i為第e個基礎模型對xi的預測結果。

堆疊法的思路是將一組基礎模型的預測結果作為訓練集，對一個簡單的頂層模型進行訓練，頂層模型輸出最終的預測結果，如圖5 所示。

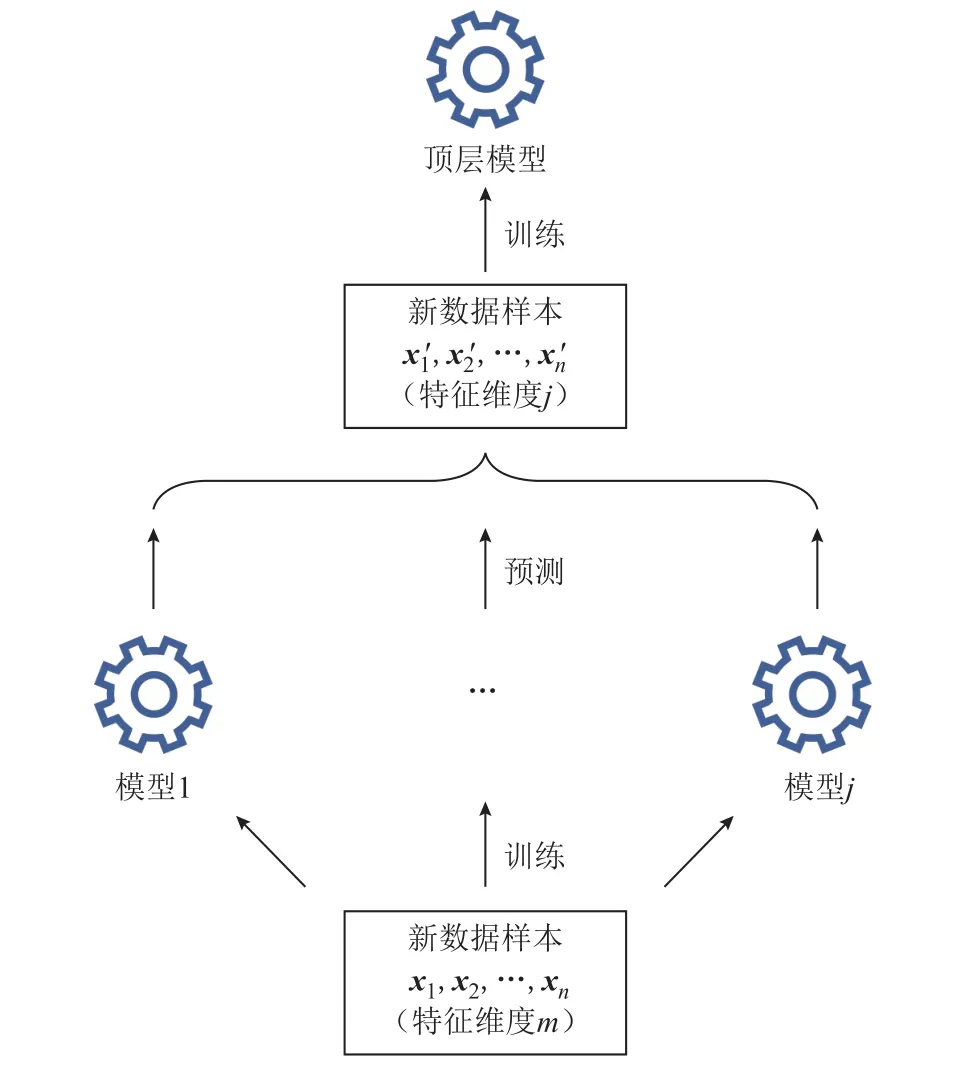
圖5 堆疊法示意圖Fig.5 Diagram of stack ensemble method

假設輸入樣本數為n，特征維度為m，存在j個底層基礎模型，基礎模型在整個訓練集上進行訓練。將它們對訓練集的預測結果當作新的訓練集傳遞給上層的一個簡單模型，那么這個新的訓練集的數目為n，特征維度為j。一般來說j要遠小于m，且底層模型預測的結果與目標輸出更加接近，頂層模型能夠利用維度更少的、質量更好的數據集進行訓練，從而實現整體上更精準的預測。

需要說明的是，集成方法的基礎模型應盡量選擇相互獨立的不同算法，這樣有利于提升集成模型的整體性能。本文采用SVR、XGBoost 和隨機森林作為基礎模型，三個模型采用的算法完全不同且都廣泛應用于回歸問題。具體而言，XGBoost 采用了梯度提升的算法，因此能夠在訓練集上實現更小的誤差，但相應地模型更容易過擬合；SVR 和隨機森林在訓練集上的誤差相比XGBoost 而言更大，但不易過擬合、泛化能力相對更強。因此，將它們結合起來能夠有效平衡模型訓練誤差和泛化能力之間的矛盾。

3 機器學習問題與評價指標

本文所要解決的機器學習問題是：基于機器學習的方法，構建活化期電池數據與電池容量的非線性映射。數據集包括活化期電池循環放電部分的特征。在獲得模型預測的容量后，根據預測容量來對電池進行初分選，按照給定容量閾值將不合格的電池淘汰。

電池容量的預測屬于回歸問題，回歸問題常用的評價指標為平均絕對誤差（Mean Absolute Error,MAE）、方均根誤差（Root-Mean-Square Error, RMSE）和方均根百分比誤差（Root-Mean-Square Percentage Error, RMSPE）等。本文采用RMSE 和RMSPE 作為電池容量預測的評價指標，分別表示為

式中，Qi為容量的真實值；iQ′為容量的預測值。

對于電池分選，采用準確率（Accuracy）和召回率（Recall）作為評價指標，有

式中，TP 表示本身是不合格的電池而被正確預測為不合格；TN 表示本身是合格的電池且被正確預測為合格；FN 表示本身為不合格的電池卻被誤認為是合格的；ALL 表示所有電池。電池分選方法的準確率和召回率越高，其分選效果越好。

4 主要工作

本文的主要工作包括特征選擇、模型構建與優化、模型測試與驗證和電池分選四個部分。其中，本文利用Scikit-learn 庫[36]對基礎模型和集成模型進行訓練與超參數優化。對于作為對照組的神經網絡模型，采用Keras 框架進行訓練與優化。數據處理與其他編程工作均通過Python 編程語言完成。

4.1 特征選擇

當數據維度很高時，許多機器學習算法的實現會變得相當困難，這種現象被稱為維數災難（curse of dimension）。本文所使用的數據集樣本數量較少（416 個），而特征維數較高（7 個），會導致訓練得到的模型泛化能力較差。目前解決這一問題的方法大致有兩種：一是增加樣本數量，使訓練實例達到足夠大的密度；二是降低數據維度，即特征的數量。第一種方法在本問題中難以實現，因為所需要的訓練實例數量隨著維度的增加呈指數上升。因此，本文采用特征選擇的方法實現數據降維。

數據降維的目標是盡可能保留有用的、信息量大的特征，剔除冗余的、信息量小的特征。為此采用一種綜合性的特征選擇方法，通過對特征進行量化評分來選擇出最優的特征組合，在對數據降維的同時保留最有用的特征，提升訓練得到的模型性能。本方法對特征的量化評價分為四個部分：

1）根據各個特征與目標容量之間的相關系數來評價特征。相關系數主要是衡量特征與目標之間的線性相關程度。

2）根據各個特征與目標容量間的互信息[37]來評價特征。互信息主要是衡量特征與目標之間的非線性相關程度。

3）利用模型選擇的方法來評價特征。模型選擇方法通過簡單的模型對特征進行評價，而這些模型擁有可以定量化的評價指標。

4）利用順序選擇[38]的方法來評價特征。順序選擇方法是一種貪心算法，該方法逐步尋找最優的特征添加到選擇的特征集合中，根據特征添加的順序可以判斷特征的有效性。

本文提出的特征選擇方法評分準則如下：每個部分中，根據各個部分對應的評價指標對所有特征按照其有效性從高到低進行排序。在第一部分和第二部分，排名第一至第四的特征分別評分為4、3、2、1 分。在第三部分和第四部分各采用兩個模型，Lasso 回歸模型和極端隨機樹模型[39]。選擇這兩個模型的原因為：①這兩個模型都有可以量化評價特征的指標，即回歸模型的系數和樹模型的特征重要性；②這兩個模型采用完全不同的算法、相互獨立，選擇兩種模型能增加對特征評價的全面性。針對單個模型，排名第一至第四的特征分別評分為2、1.5、1、0.5 分。最終每個特征的評分總和見表2。

表2 各個特征的評分結果Tab.2 Scores of all features

從最終合計分數可以看到，放電終止電壓是最有效的特征，分數顯著超過其他特征分數；庫倫效率、放電中壓、歐姆內阻及直流內阻四個特征分數基本接近，屬于可用特征；而放電起始電壓和平臺到達時間段這兩個特征分數非常低，屬于冗余、信息量低的特征。因此，最終選擇放電終止電壓、庫倫效率、放電中壓、歐姆內阻及直流內阻5 個特征為最終訓練所用特征，數據集的維度從7 維降低到5 維。關于特征選擇的有效性，將在本文4.3.2 節進行檢驗。

4.2 模型構建與優化

4.2.1 基礎模型訓練與超參數優化

在進行模型的集成與訓練之前，需要對三個基礎模型SVR、XGBoost 和隨機森林進行超參數優化以獲取各個模型的最優超參數。更優的超參數能夠提升模型性能、提升模型泛化能力并減小其預測的誤差。

本文采用網格搜索的方法對模型的超參數進行優化，針對給定的參數搜索空間尋找最優超參數組合。為了評價模型在不同超參數組合下的參數優劣，本文采用三折交叉驗證方法。具體為，將訓練集劃分為等樣本數量的三個部分，對模型進行三輪訓練與評估。每一輪訓練時，選擇不同的一折樣本作為驗證集來評價模型，剩下的兩折用來訓練模型。由于驗證集沒有用作模型訓練，模型在驗證集上的分數能夠反映模型的泛化能力與整體性能，是可信的評價指標。

模型的訓練與評價流程如圖6 所示，本文采用RMSE 作為模型驗證分數。將模型在三折交叉驗證中三個驗證集上的RMSE 分數進行平均即可得到該分數，該分數越小代表該模型的超參數越優。對于超參數空間的每一個組合，都進行一次三折交叉驗證得到模型驗證分數，直到窮舉完模型所有的超參數組合。最優的模型驗證分數對應的超參數組合就是最終的模型最優超參數。

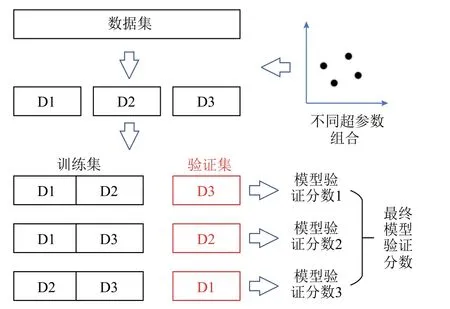
圖6 模型的超參數優化過程Fig.6 Process of hyperparameters’ optimization

經過網格搜索優化后，三個基礎模型的各自的最優超參數和最優模型驗證分數見表3。各個模型所選擇的可調整超參數都是模型比較有代表性的關鍵參數與正則化參數。比如，XGBoost 和隨機森林的超參數都是用來控制組成模型的決策樹的數量和復雜程度，而SVR 的Gamma 和C參數則分別控制模型對數據的擬合程度和對誤差的容忍程度。因此通過控制這些關鍵超參數的取值就能有效地控制模型在訓練后的復雜程度、誤差大小與泛化能力。

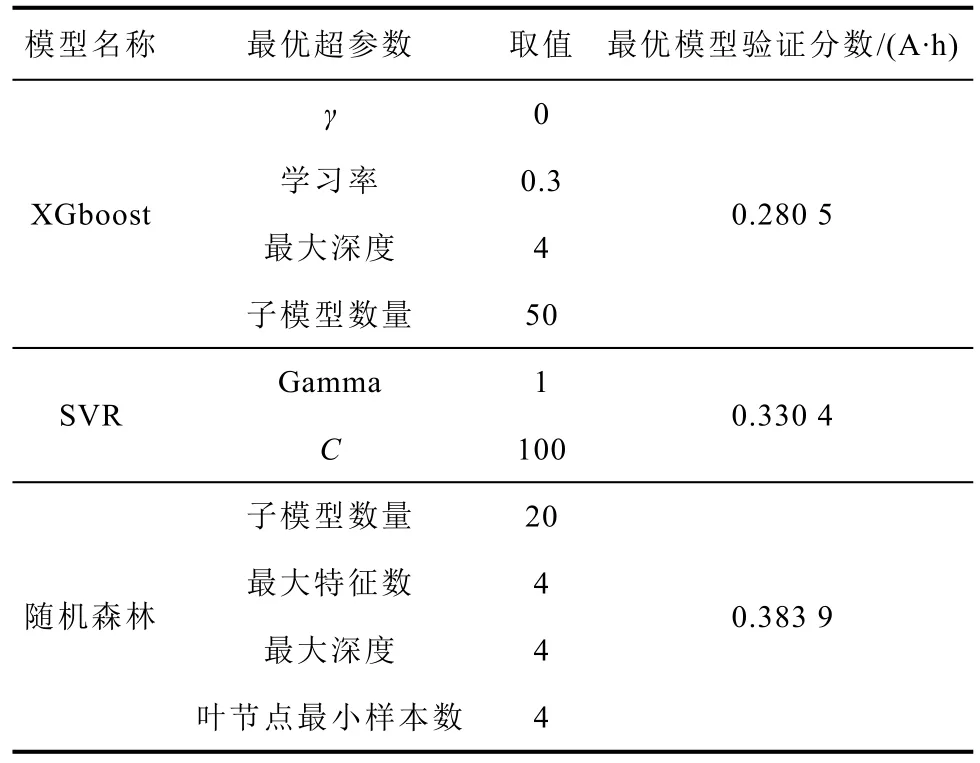
表3 各基礎模型的最優超參數取值與模型驗證分數Tab.3 Best hyperparameters and model validation scores of each model

三個模型的最優模型驗證分數分別為0.280 5、0.330 4 和0.383 9 A·h。從最終的最優模型驗證分數來看，具有最優超參數的三個模型的預測效果良好，電池預測的平均誤差在0.4 A·h 以內，相對誤差小于0.8%。從結果可知XGBoost 模型是性能最佳的基礎模型。

4.2.2 集成模型訓練與驗證

在獲取基礎模型的最優超參數后，進一步對集成模型進行訓練。對于投票集成模型，除基礎模型外不需要額外的模型。對于堆疊集成模型，除了基礎模型之外，還需要一個模型作為頂層預測器。本文采用L2正則化的線性模型嶺回歸模型作為頂層預測器。為了體現集成方法的有效性，同樣對兩種集成模型進行三折交叉驗證。兩個集成模型和基礎模型的模型驗證分數見表4。

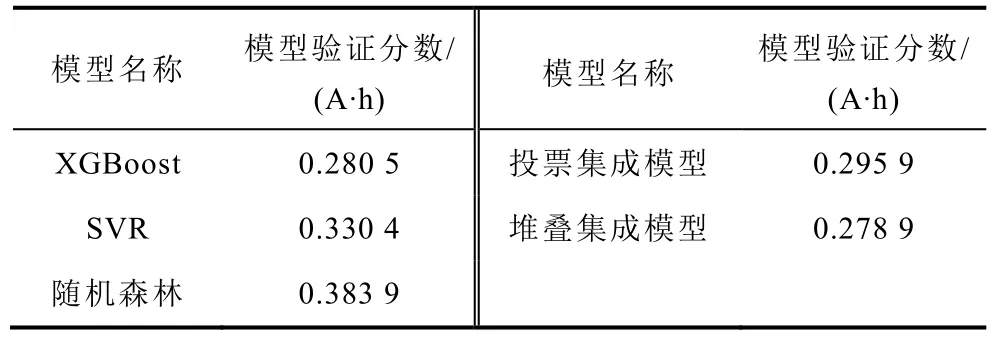
表4 基礎模型和集成模型的模型驗證分數Tab.4 Model validation scores of base models and ensemble models

從表4 可知，堆疊集成模型的效果最優；投票集成模型的性能雖然也比較好，優于SVR 和隨機森林模型，但仍弱于最優的基礎模型XGBoost。

4.3 模型測試與驗證

4.3.1 測試集上的測試與結論

在獲得集成模型的模型驗證分數進行初步判斷后，將兩個集成模型在整個訓練集上進行訓練得到最終的完整模型。對于基礎模型，同樣使用最優超參數在整個訓練集上進行訓練得到最終基礎模型，用來檢驗集成方法是否提升了模型性能。為了進一步體現集成模型的優越性，本文訓練了一個額外的神經網絡模型作為對照組。該神經網絡具有兩個隱藏層，每個隱藏層的神經元數目為32 個。此外，該神經網絡模型是經過三折交叉驗證與網格搜索調整后的最優模型，擁有最優的網絡結構與超參數，可以作為衡量集成模型性能的基準。

將所有模型在測試集上進行評估，得到基礎模型、集成模型和對照模型（神經網絡模型）的測試集分數，以評價模型的泛化能力。測試集分數為RMSE 和RMSPE，用來衡量預測容量同真實容量之間的誤差。分數越小，代表模型誤差越小、性能越好。最終結果見表5。

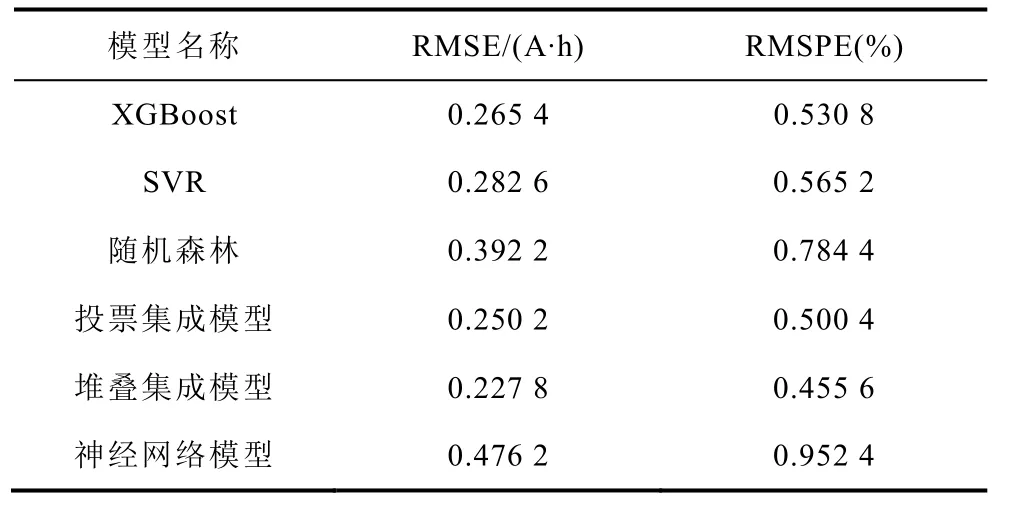
表5 所有模型在測試集上的分數Tab.5 Scores of all models on the test set

由表5 可知，兩個集成模型的測試誤差均小于基礎模型及對照模型，由此可見集成方法確實能有效提高模型的泛化能力、減小預測誤差。同時，堆疊集成方法比投票集成方法在本問題上更優，預測誤差為0.227 8 A·h 和0.455 6%，實現了對電池容量高精度的預測。

對于電池分選而言，除了關注模型對容量預測的整體誤差，也要考察其出現較大誤差的概率。如果模型出現較大誤差的概率過高，即使整體誤差較小也不能有效地進行電池分選。所有模型在測試集84個樣本上的預測值與真實值的絕對誤差如圖7 所示，其中藍色虛線表示絕對誤差為± 0.75 A·h 的邊界線。可以看到，即便所有模型的整體預測誤差都較小，對于個別樣本依然存在誤差較大的情況。比如對于第83 個樣本，所有模型的絕對誤差都超過了0.75 A·h。

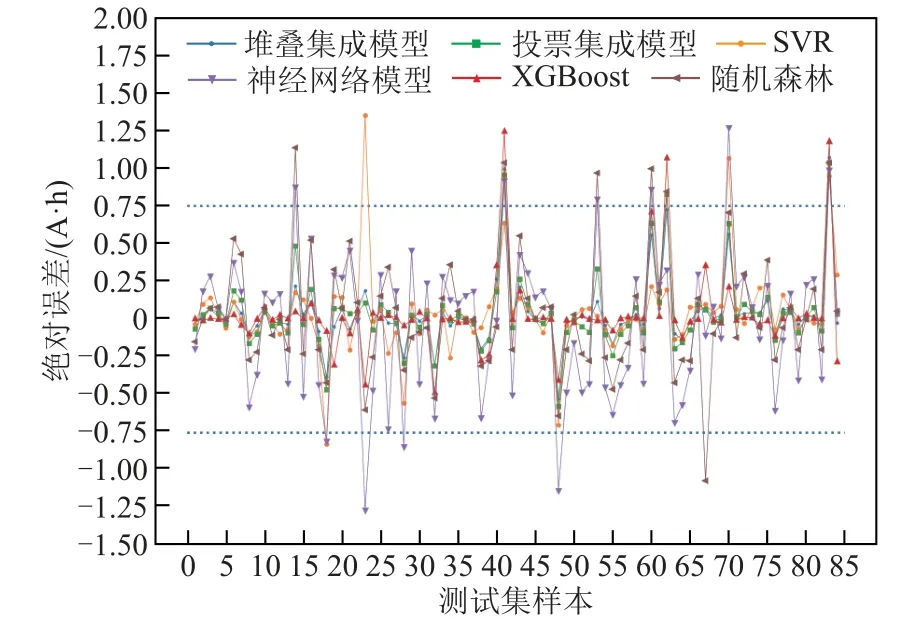
圖7 基礎模型、集成模型和對照模型在測試集各樣本上的絕對誤差Fig.7 Absolute errors of each model on the test set

考慮到神經網絡模型在本文中為對照模型，其在測試集上的RMSE 分數為0.476 2 A·h。因此，本文選擇采用其RMSE 的1.5 倍左右的數值作為預測失效的閾值，即0.75 A·h，并規定當模型超越誤差上限時模型失效。

各個模型在測試集上出現超越誤差上限的次數與頻率可以用來衡量模型的可靠性。本文利用失效頻率來估計失效概率，然后根據失效概率計算模型的可靠性。各個模型的失效次數、失效頻率和可靠性見表6。

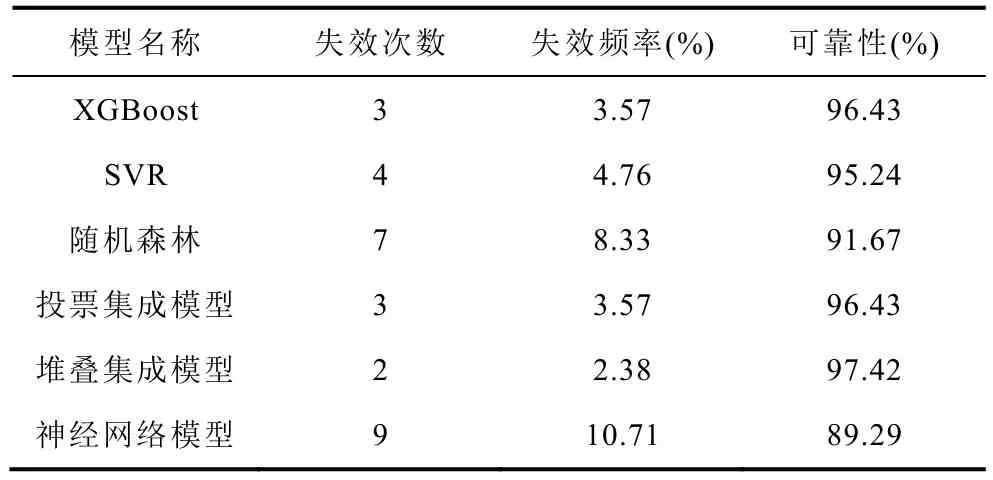
表6 所有模型在測試集上可靠性評估Tab.6 Reliability evaluation of all models on the test set

從失效次數和頻率來看，堆疊集成模型是最優的，僅失效2 次、失效頻率為2.38%。從模型的可靠性層面來看，集成方法也能有效地改善模型的可靠性。相較于主流的有監督學習方法（神經網絡模型），堆疊集成模型的預測誤差顯著降低，降低了52.16%；可靠性有了一定的提升，提升了9.10%。因此本文最終選擇堆疊集成模型作為分選模型用來預測滿放容量。

為了進一步檢驗根據測試集檢驗所得到的最優模型堆疊集成模型的泛化能力，本文采用三個50 A·h Li||Sb-Sn 液態金屬電池，電池活化期循環數據均未用于訓練和測試。電池穩定滿放容量分別45.22 A·h、47.28 A·h 和48.97 A·h，總共有57 個活化期循環樣本。最終堆疊集成模型在額外電池數據集上的RMSE 和RMSPE 分數分別為0.320 6 A·h 和0.641 2%，失效次數為4 次，可靠性為92.98%。盡管由于額外電池數量比較少，且與訓練測試用電池容量分布不同，模型在該數據集上的整體性能比測試集差，但從驗證結果來看，堆疊集成模型依然是有效的，在不同于訓練與測試的電池上仍擁有較小的預測誤差和較好的可靠性。

4.3.2 特征選擇方法有效性驗證

為了評價在訓練模型之前特征選擇的有效性，本文設置了一個對照組實驗，即在不進行特征選擇的情況下，對基礎模型進行超參數優化、集成模型訓練和測試集測試。對比結果如圖7 所示。

由圖8 可知，無論是模型驗證分數，還是測試集上的分數和失效次數，經過特征選擇后的基礎模型與集成模型的表現是全方位更優的，在相同類型的模型下誤差更低、失效次數更少，表明本文所提出的特征選擇方法的有效性與必要性。

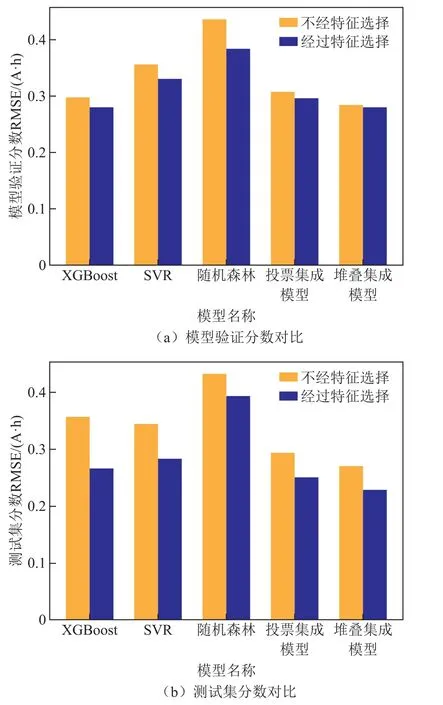
圖8 經過特征選擇與不經過特征選擇的模型性能對比Fig.8 performance comparison between models with feature selection and models without selection

4.4 電池分選結果

本節基于堆疊集成模型進一步預測了電池容量并進行電池分選，將容量大于或等于48 A·h 的電池視作合格，小于48 A·h 的電池視作不合格。本文在選擇該閾值時主要考慮了樣本數據的分布與電池性能。根據大量正常運行的電池樣本數據分布，大部分電池樣本集中在48 A·h 附近。將48 A·h 作為閾值，能更加考驗模型容量預測的精度與可靠性。同時，電池在容量大于等于48 A·h 時性能更加穩定，因此綜合考慮選擇48 A·h 作為閾值。

現對訓練測試用的24 個電池的所有循環通過堆疊集成模型進行預測，根據預測結果進行電池分選。其分選結果見表7。

表7 整個數據集的分選結果（混淆矩陣）Tab.7 Sorting results on the whole dataset (confusion matrix)

從表7 可知，實際情況與預測結果的重合度非常高，絕大部分樣本集中在混淆矩陣的右對角線上（即TN 和TP），表明該方法對絕大多數的電池循環作出了正確的判斷。

根據最終的混淆矩陣可知，電池分選的準確率達到了96.62%。且對于不合格電池混入合格電池的情況，即對不合格電池的召回率，堆疊集成模型的預測結果達到了93.18%，滿足分選的精度要求。

為了進一步驗證該模型在電池分選中的有效性，對4.3.1 節中的額外電池數據通過堆疊集成模型進行預測與分選，在57 個樣本上的分選的準確率和召回率均為100%。這充分說明了該集成模型在分選中的應用潛力。

5 結論

針對液態金屬電池的快速準確分選問題，本文提出了一種基于集成學習的機器學習模型，通過特征選擇和集成學習的方法，實現了電池容量的精確預測和電池的準確分選，研究結果表明：

1）基于集成模型預測容量對電池的分選方法是準確高效的。該方法不僅利用活化期的數據節省了大量的測試時間，也通過高精度的集成模型實現了高準確率和高召回率的電池分選，準確率達到了96.62%，召回率達到了93.18%。

2）本文提出的綜合特征選擇方法是有效的。與沒有進行特征選擇所得到的模型相比，選擇后訓練得到的模型無論是在基礎模型上還是在集成模型上都實現了全面的性能提升，擁有更小的誤差和更高的可靠性。

3）經過模型驗證分數、測試集測試分數和可靠性等指標檢驗，本文提出的集成模型性能不僅優于用于集成的基礎模型，也優于對照組的主流神經網絡模型。相較于主流的有監督學習方法（神經網絡）模型，所提出的集成模型的預測誤差有了顯著降低，降低了52.16%；可靠性有了一定的提升，提升了9.10%。這充分說明了集成方法的有效性。最優的堆疊集成模型實現了對電池滿放容量的高精度預測，在測試集上的RMSE 和RMSPE 僅有0.227 8 A·h 和0.455 6%，可靠性達到97.42%。

本文提出的方法可用于液態金屬電池的快速分選，為電池的分選重組提供高精度與可靠的分選指標。相關的研究方法，比如特征選擇方法與集成學習方法，同樣可以遷移到其他體系的儲能電池的分選研究中。