基于分裂Bregman全變分算法的金標試紙圖像去噪研究

賀鳳娟 陳偉利

（吉林建筑大學電氣與計算機學院，吉林 長春 130118）

1 引言

金標試紙一般采用兩種方法制備而成：雙抗體夾心法和競爭法。本文實驗選取的試紙條是由競爭法制備的，圖1為競爭法金標試紙結構組成，由左至右分別為樣品點、結合墊、檢測線(T線)、NC膜、質控線（C線）以及吸水紙。當T線顏色比C線顏色淺，表示為陽性；當T線顏色比C線顏色深，表示為陰性。盡管金標試紙檢測方便迅速，但是它只能定性分析。金標試紙的定量分析引起廣泛關注，現如今開發定量分析設備都離不開對金標試紙圖像的處理。圖像采集設備獲取金標試紙圖像時，由于傳感器內部結構和外部環境因素的影響使獲取的金標圖像存在較多噪聲，這對后續的試紙定位和特征值提取有很大的干擾。因此，金標試紙圖像去噪處理對金標試紙定量分析起到至關重要的作用。現如今大多金標試紙定量分析儀多采用中值濾波算法[1-3]進行降噪處理，該算法受濾波窗口尺寸影響較大，容易造成圖像不連續，對于定量分析精度要求高的硬件設備來說不太理想。為了更好地消除金標試紙圖像的噪聲，本文將結合各向同性和異性的擴散原理對分裂Bregman迭代的全變分算法進行改進，利用改進的算法對林可霉素金標試紙圖像進行降噪處理。

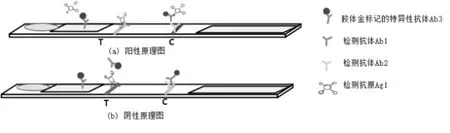
圖1 競爭法金標試紙原理圖

2 獲取金標試紙圖像

本文涉及的實驗均以林可霉素免疫層析試紙條作為目標樣本，奶類中定量檢測林可霉素為食品安全做出了重要貢獻。取200uL不同濃度的林可霉素稀釋液分別滴入同一生產批林可霉素金標樣品墊上。反應結束后用OV2640捕獲不同濃度的金標試紙圖像。本文目標是將試紙圖像中的噪聲精準剔除，為后續實現精確分割T線和C線做鋪墊。

3 基于分裂Bregman算法的全變分圖像去噪

金標試紙存在噪聲有許多因素，首先是金標試紙在發生免疫反應時，由于溫度、濕度以及抗原抗體反應物滲透不均等因素的影響，導致圖像本身具有一定的噪聲[1-3]。這對于后續提取T線和C線的特征值建立濃度曲線有很大的干擾，因此定量分析金標試紙圖像需要一種有效的圖像去噪算法。Tom Goldstein和Stanley Osher于2009年首次提出：結合各向同性擴散和各向異性擴散性質，應用分裂Bregman算法解決L1正則化優化問題，文章中分別討論了基于Bregman各向異性全變分（SBITV）算法和基于Bregman各向異性全變分(SBATV)算法[4]。但是該算法只是加速了各向同性全變分(ITV)和各向異性全變分(ATV)的求解問題，并沒有解決ITV去噪導致的圖像邊緣模糊問題和ATV去噪導致的圖像存在偽輪廓現象[5,10-11]。因此,本文融合各向同性擴散使圖像平滑以及各向異性保留邊緣信息的優點，應用分裂Bregman算法加速全變分算法的求解。

目前，基于分裂Bregman全變分算法的圖像降噪還沒有在金標圖像處理中應用，本節討論如何將各向同性擴散和各向異性擴散性質融合入分裂Bregman全變分算法中，對金標試紙圖像進行去噪，填補該算法在這一領域應用的空缺[6]。

3.1 分裂Bregman全變分算法（SBTV）

討論分裂Bregman全變分算法前，我們需要了解Bregman距離和Bregman迭代算法，Bregman距離公式如下：

Bregman迭代算法基本模型如下，其中A為線性算子，b為向量：

分裂Bregman算法處理L1正則化問題的常用形式：

引入Bregman距離d使d=φ(u)，將式4改寫為非約束問題：

綜合公式1～5，得到分裂Bregman公式：

因為分裂Bregman算法使式6的L1范數和L2范數分裂，所以可把式6分解為兩個子問題：

3.2 基于分裂Bregman各向異性全變分(SBATV)

公式10為SBITV去噪模型的無約束形式，u為原始圖像；g為u的噪聲圖像：

然后應用公式5SBTV算法得到公式11：

應用公式8解決式11的最小化問題，得到公式12：

公式12的目的是使u平滑，即求解u的最小值，所以令u的一階變分導數為零，得到：

然后應用Gauss-Seidel方法求解u問題：

根據式11可知，dx、dy元素之間沒有耦合，所以d問題可以使用收縮算子求解即可得到，dy與dx形式相同，將下標x改為y即可：

根據公式7，解決b問題：

3.3 基于分裂Bregman各向同性全變分(SBITV)

公式17為SBATV去噪模型的無約束形式，u為原始圖像；g為u的噪聲圖像：

各向同性擴散性質與各向異性擴散性質應用SBTV求解過程基本相似，唯一不同的是應用各向同性擴散性質的d元素之間沒有解耦，所以對于d問題的求解有所不同。對于d最小化問題：

以上是SBATV和SBITV的推導過程，具體內容詳見參考文獻[4-5,7-11]。

3.4 改進的基于分裂Bregman全變分

3.1 節至3.3節詳細介紹了各向異性擴散和各向同性擴散性質在SBTV中的推導過程。當把SBITV和SBATV實際應用到林可霉素金標試紙，結果顯示前者導致T線和C線的邊緣模糊，后者導致T線和C線產生階梯效應。為了更好地消除金標試紙圖像的噪聲，使T線和C線能保留邊緣信息且不會產生偽輪廓現象，于是將各向同性擴散性質的d元素的求解與各向異性擴散性質的d元素的求解按一定權重相加，則改進的去噪模型如下：

本文改進的算法本質上是對d問題求解過程的改進，對于u問題和b問題的求解過程與SBITV和SBATV的推導過程相同。對于d的最小化問題，公式15解出各向異性擴散性質的，公式19求出各向同性擴散性質的得到公式22，dy與dx形式相同，將下標x改為y即可。

所以改進的算法求解如下：

步驟1初始化u=0,b=0,d=0；

步驟2利用公式15和公式19分別求出各向異性擴散性質和各向同性擴散性質的dx和dy，然后代入公式22求出d問題；

步驟3利用公式14的Gauss-Seidel方法求解u問題；

步驟4更新bx，by的值；

步驟5如果‖uk-uk-1‖2>Tol，則跳至步驟2繼續迭代，否則迭代結束。

4 實驗結果和分析

為了驗證該算法對于金標試紙去噪處理的優越性，利用Matlab 2021b軟件編寫SBITV、SBATV、中值濾波以及本文改進的算法處理同一批林可霉素金標試紙圖像，實驗環境配置為Intel(R)Core(TM)i5-10200H CPU@2.40GHz 2.40 GHz處理器，機帶RAM 16.0GB，64位操作系統的計算機上。

通過比較不同算法的圖像視覺效果和圖像去噪數值指標的優劣，分析改進算法的優缺點。實驗獲取的金標試紙圖像分辨率為230×90，其中去噪參數γ=0.1，β=0.2，各向異性和各向同性的權重w1=0.9，w2=0.1，中值去噪算法的模板為4×4。

4.1 圖像視覺效果對比

在實際應用中，由于外界環境、圖像采集設備硬件電路設計等因素的影響，導致獲取的金標試紙圖像存在噪聲。因此給林可霉素試紙圖像添加10dB高斯白噪聲（圖2）、方差為0.08的乘性噪聲（圖3）和椒鹽噪聲（圖4），分析不同濃度的林可霉素試紙在不同噪聲干擾下的圖像，評估三種算法的視覺效果。

圖2 高斯白噪聲的去噪圖像

圖3 乘性噪聲的去噪圖像

圖4 椒鹽噪聲的去噪圖像

從圖2(c)、圖3(c)和圖4(c)可以看出在三種不同噪聲的干擾下，雖然SBATV去噪后的圖像T線邊緣和C線邊緣比相應噪聲圖像略清晰，但是SBATV去噪后圖像整體產生許多細微的馬賽克，導致圖像失真。可能是金標試紙原始灰度圖像的量化等級太少，圖像層次欠豐富，因此出現了偽輪廓現象。圖2(e)、圖3(e)和圖4(e)是經SBITV算法去噪后的圖像，SBITV去噪后的圖像與本文改進的算法去噪圖像相比。SBITV去噪后的圖像T線和C線相對模糊，在T線和C線邊緣處可以明顯觀察到經SBITV算法去噪后邊緣不清晰。圖2(f)、圖3(f)和圖4(f)是中值濾波后的圖像，對比三種噪聲干擾下中值濾波處理后的金標試紙圖像，觀察到中值濾波處理乘性噪聲和椒鹽噪聲的視覺效果更好。但處理高斯白噪聲時，明顯觀察到金標試紙圖像的T線和C線邊緣模糊。圖2(d)、圖3(d)和圖4(d)是改進的算法去噪后的圖像，改進的算法克服了SBITV導致的圖像邊緣模糊問題以及SBATV產生的階梯效應，不但消除了噪聲而且保留了金標試紙圖像的T線和C線細節信息，獲得了優越的降噪性能。

綜合對比圖2、圖3和圖4在三種不同噪聲干擾下的去噪圖像，可以看出改進的算法是四種去噪算法中保留金標試紙圖像結構和邊緣信息最為完整的去噪算法，該算法處理后的圖像和原始圖像視覺效果相似度最高。所以在金標試紙圖像去噪視覺效果上，改進的算法去噪效果最完善。

4.2 圖像去噪數值指標

為了更準確地評估噪聲去除效果，通過引入峰值信噪比（PSNR）作為評估四種算法的圖像去噪數值指標。其中PSNR計算公式為：

圖像數據為8位無符號整數時：n=8，MSE為原始圖像與去噪圖像之間的配給平方誤差。去噪效果與PSNR值成正相關，PSNR的值越大，代表該算法的去噪效果越好[6,11]。

從圖5、圖6和圖7可以看出，在數值指標上，觀察到改進的算法去噪的數值指標明顯要比其它三種算法的去噪效果更好，其中SBATV的效果最差。高斯噪聲干擾下，改進的算法PSNR值約為64dB，比SBITV、SBATV和中值濾波的PSNR值分別增大了約4dB、25dB和22dB；乘性噪聲干擾下，改進的算法PSNR值約為56dB，比SBITV、SBATV和中值濾波的PSNR值分別提高了約2dB、20dB和15dB；椒鹽噪聲干擾下，改進的算法PSNR值約為58dB，比SBITV、SBATV和中值濾波的PSNR值分別上升了2dB、20dB和16dB左右。因此可以得出結論：改進的算法在數值指標上對金標試紙圖像去噪效果更優。

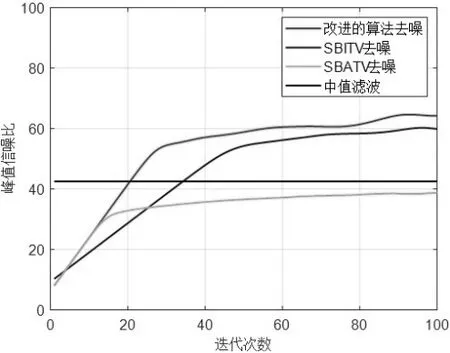
圖5 林可霉素高斯白噪聲PNSR圖像

圖6 林可霉素乘性噪聲PNSR圖像

圖7 林可霉素椒鹽噪聲PNSR圖像

5 結語

本文在研究SBATV和SBITV對林可霉素金標試紙圖像去噪的基礎上，成功將兩者算法的各向同性擴散性質和各向異性擴散性質融合到分裂Bregman全變分算法中，該算法極大改善了SBATV導致的金標試紙圖像T線和C線處產生的偽輪廓現象，同時優化了SBITV導致的金標試紙圖像模糊。并從圖像去噪視覺效果和圖像去噪數值指標兩方面對比改進的算法、SBATV、SBITV以及中值濾波。我們可以得出結論：在三種不同噪聲干擾下，改進的算法對金標試紙圖像的去噪視覺效果和去噪數值指標最優。改進的算法應用到金標試紙圖像去噪具有很大的優勢。它的計算復雜度低，能夠顯著提高金標試紙圖像的質量，保留T線和C線的紋理信息。高精度的去噪有利于后續進行T線和C線的分割和特征值的提取，這為提高金標定量分析設備的精度提供了一種有效的方法。