基于廣義正態分布算法優化支持向量機的電機軸承故障診斷研究

陳鑫洋 李水明

（柳州鐵道職業技術學院，柳州 545616）

隨著工業的發展，電機軸承在旋轉機械設備中得到廣泛應用。但是，大多數旋轉機械設備通常在滿負載的條件下運行，而且工作環境極為惡劣，導致電機軸承損壞加劇，如果不及時處理，會導致設備損壞，甚至對操作人員的人身安全產生嚴重威脅。因此，研究一種高精準度的算法來識別故障零件十分必要。

旋轉機械設備的故障診斷問題，一直是國內外專家的研究熱點。崔建國等通過使用改進的灰狼算法（Improved Grey Wolf Optimization，IGWO）來優化核極限學習機（Kernel Based Extreme Learning Machine，KELM），對航空發動機進行了故障診斷技術研究[1]。張婕等通過將變分模態分解（Variational Mode Decomposition，VMD）與精細復合多尺度均值散布熵（Refined Composite Multiscale Mean Dispersion Entropy，RCMMDE）相結合的形式，提取電機軸承的故障特征數據，以此提高診斷精度[2]。

為了準確辨別旋轉機械設備的故障振動信號，提出一種基于廣義正態分布優化（Generalized Normal Distribution Optimization，GNDO）的支持向量機（Support Vector Machine，SVM）算法，并通過實驗證明了GNDOSVM 算法在故障診斷中的有效性和準確性。

1 GNDO-SVM 算法

1.1 廣義正態分布優化算法

GNDO 算法是一種基于正態分布的優化算法，用于解決連續型優化問題[3]。GNDO 算法通過模型建立和分布采樣來平衡全局尋優和局部尋優，在一些復雜的優化問題中體現其優越性和準確性[4]。

1.1.1 局部尋優

局部尋優的過程通過式（1）～式（4）來展現。

式中：a、b、λ1和λ2均為rand（1），表示0 ～1的隨機數。

1.1.2 全局尋優全局尋優的過程通過式（5）～式（8）來展現。

式中：λ3和λ4為滿足高斯分布的隨機數；β為rand（1）；v1和v2為軌跡向量。

式中：p1、p2和p3分別為rand（1,N），表示1 ～N的3 個隨機整數，且p1≠p2≠p3。為了避免算法陷入局部最優解，GNDO 算法在尋優過程中設計了一種篩選機制，即

1.2 支持向量機算法

SVM 算法是一種基于統計學理論的機械學習算法，主要思路是通過在特征空間中找到一個超平面，并有效分開不同類別的數據點。SVM 算法工作原理如下。

式中：ω和ξi分別為權重向量和松弛因子；a'和b'分別為懲罰因子和算法的部分向量。

SVM 算法對于數據分類問題的最終表達式為

式中：W(c')為分類目標函數；c'為對偶變量；y為樣本；h為標簽；K(hi,hj)為SVM 算法的核函數。

本文選用徑向基作為算法的核函數，即

式中：g為SVM 算法的核函數參數。

1.3 GNDO-SVM 算法

為了進一步提高SVM 算法的泛化性和準確性，使用GNDO 算法對其進行尋優求解，找到最佳參數組合[c'best,gbest]，以此推導出GNDO-SVM 算法，提高算法對電機軸承數據故障診斷的準確性[5]。GNDOSVM 算法具體步驟如下。

（1）數據集、種群初始化。將數據集分為訓練集和測試集，并對其進行歸一化處理，初始化GNDO算法的種群數量、尋優范圍以及最大迭代次數。

（2）設計適應度函數并進行尋優求解。以歸一化訓練集的分類準確率作為適應度函數，并通過GNDO算法對其尋優求解，獲取迭代中的最優個體xbest。

（3）更新個體位置。通過GNDO 算法篩選機制更新種群個體位置，并計算種群最優適應度值來更新xbest。

（4）判斷GNDO 算法是否迭代完成。若GNDO算法沒有達到最大迭代次數，將重復步驟（2）～（3）。反之，若GNDO 算法達到最大迭代次數，算法將輸出xbest=[c'best,gbest]給SVM 算法，并對測試集進行檢測。

2 電機軸承故障診斷實驗驗證

為了驗證GNDO-SVM 算法在電機軸承故障診斷中的有效性和準確性，以美國凱斯西儲大學的電機軸承數據作為實驗對象，并與基礎SVM 算法進行對比分析。文中共選取3 種軸承故障數據和1 種正常軸承數據作為實驗對象，其中3 種故障數據包含2 種不同的故障程度，分別為0.18 mm 和0.36 mm。利用加速度傳感器在采樣頻率為12 kHz 和負載功率為0 kW 條件下，采集7 種振動信號。

本研究采用時域特征提取的方式提取振動信號的特征，以此構成時域特征故障數據集，使算法更好地對電機軸承故障振動信號進行分類。時域特征分別為信號的方差、均值、均方根值、偏度、峭度、波性指標、裕度指標、脈沖指標、峰值指標以及峭度指標，本研究具體特征曲線如圖1 所示。

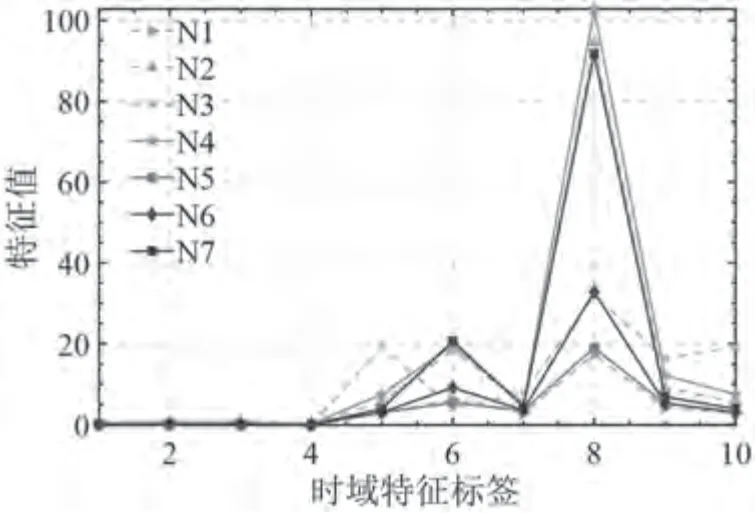
圖1 振動信號時域特征曲線

為了更加生動形象地觀測兩種算法的準確率，建立故障分類結果點圖和熱力圖，分別如圖2 和圖3 所示。

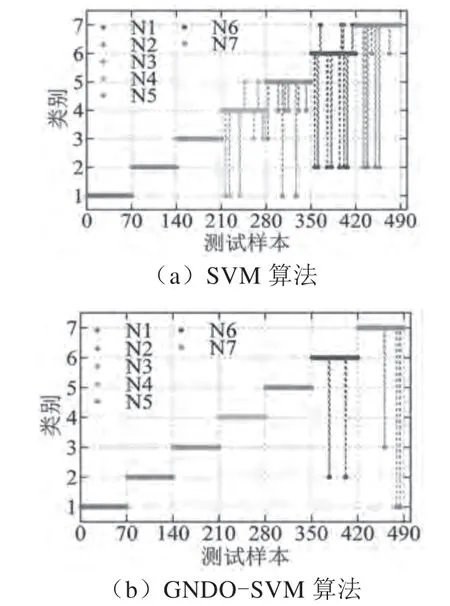
圖2 故障分類結果點圖

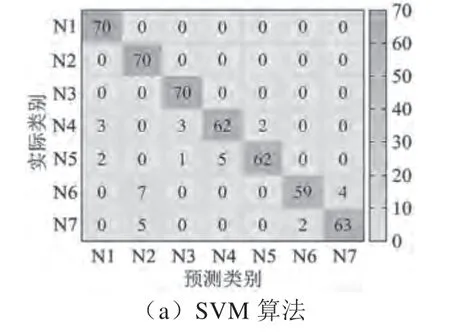
圖3 故障分類結果熱力圖

SVM 算法對電機軸承故障振動信號的識別率低于GNDO-SVM 算法，共計有34 個故障樣本識別錯誤，而GNDO-SVM 算法僅有5 個故障樣本識別錯誤，錯誤分類樣本個數減少29 個。通過熱力圖可以計算出SVM 算法的故障識別準確率為95.1%，而GNDOSVM 算法故障識別準確率為99%，其準確率相較于SVM 算法提高了3.9 個百分點。上述實驗結果表明，與基礎的SVM 算法相比，提出的GNDO-SVM 算法可以更好地提供支持向量機的最優參數，以此提高電機軸承故障分類的準確率。

3 結語

SVM 算法在對電機軸承進行故障診斷時，其c'參數和g參數的選取會嚴重影響診斷的準確率。針對這一現象，采用GNDO 算法對SVM 算法尋優求解，以此解決參數選取問題。為了進一步驗證GNDOSVM 算法在故障診斷中的準確性，本研究以凱斯西儲大學的電機軸承數據作為實驗對象，并與基礎支持向量機進行對比分析。結果表明，GNDO-SVM 算法的故障識別率高于SVM 算法，可以準確地對軸承故障進行分類，實際應用前景較為廣闊。