土工構筑物的逆幾何可靠性分析算法

吳興征 劉赫

DOI： 10.11835/j.issn.2096-6717.2021.176

收稿日期：2021?06?15

基金項目：河北省自然科學基金（E2019201296）；河北省高等學校科學技術研究重點項目（ZD2018216）；一省一校專項資助（801260201262）。

作者簡介：吳興征（1971- ），男，博士，副教授，主要從事巖土、防洪與海岸工程的不確定性模型研究，E-mail：xingzhengwu@163.com。

Received： 2021?06?15

Foundation items： Hebei Natural Science Foundation （No. E2019201296）; Key Project of Science and Technology Research in Colleges and Universities of Hebei Province （No. ZD2018216）; Advanced Talents Incubation Program of the Hebei University （No. 801260201262）.

Author brief： WU Xingzheng （1971- ）， PhD， associate professor， main research interests： uncertainty models in geotechnical， flood defence and coastal engineering， E-mail： xingzhengwu@163.com.

摘要：針對特定場地下土工構筑物的正常使用極限狀態，考慮鉆孔灌注樁、抗浮錨桿或CFG樁單樁荷載-位移測試曲線之間的離散性，將測試曲線擬合得到的回歸參數集視作隨機變量，基于幾何可靠性算法框架，運用高斯Copula函數聯合分布模型實施由標準正態空間到原始物理空間中隨機變量的表征轉換，構建基于概率密度等值線的逆幾何可靠性算法。該算法假定描述隨機變量服從正態分布的某一參數（均值或變異系數）未知，給定目標可靠指標，可推求隨機變量的概率密度等值線。通過極限狀態方程限定概率密度等值線的幾何輪廓，可求解特定目標可靠指標下隨機變量的未知均值或變異系數，并求出相應的安全系數。當隨機變量服從其他非正態邊緣分布時，等值線的幾何輪廓仍由一系列離散點近似表征，逆可靠性分析同樣適用。建議的算法主要用于解決隨機變量部分統計參數缺失或不完備的難題，給定目標可靠指標時可根據構筑物重要性等級進行安全系數校準。

關鍵詞：逆幾何可靠性；概率密度等值線；安全系數；高斯Copula函數

中圖分類號：TU473.1 ? ? 文獻標志碼：A ? ? 文章編號：2096-6717（2023）05-0106-10

Inverse geometric reliability analysis algorithm for geotechnical structures

WU Xingzheng， LIU He

（College of Civil Engineering and Architecture， Hebei University， Baoding 071002， Hebei， P. R. China）

Abstract： For serviceability limit state of geotechnical structures at a specific site， the scatter among the load-displacement curves of bored piles， floating anchors or CFG piles is considered， and the set of regression parameters obtained by fitting these test curves is treated as a random variable. On the basis of theoretical framework of the geometric reliability method， a Gaussian Copula function is used to facilitate the transformation of random variables from the standard normal space to the original physical space， and then an inverse reliability algorithm based on probability density contours （PDCs） is constructed. In this algorithm， if one parameter of a normal probability density distribution is unknown， such as the mean or coefficient of variance， the PDC of the random variables can be derived when a target reliability index is specified. If the PDC is bounded by the limit state equation， the unknown mean value or coefficient of variance for the random variable under a given target reliability index is solved， and the corresponding safety factor is derived. While a non-normal marginal distribution is followed by random variables， the geometric configuration of the PDC can be still approximated by a set of discrete points， and the inverse reliability analysis is also applicable. The proposed algorithm is mainly used to solve problems with statistical parameters of random variables ?missing or incomplete. When the target reliability index is specified， the safety factor can be calibrated according to the importance hierarchy of the structure.

Keywords： inverse geometric reliability； probability density contour； safety factor； Gaussian Copula function

可靠性分析可細分為正分析與反分析兩類。前者通過建立構筑物的極限狀態方程求解可靠指標或失效概率，據此核算構筑物是否滿足規范設定的量值。在給定目標可靠指標的情況下，后者根據構筑物的極限狀態方程進行逆分析，反求待定參數或隨機變量。反分析在部分輸入變量待定的情況下尤為適用，亦稱作逆可靠性分析，旨在解決隨機變量部分統計參數缺失或不完備的難題。此外，在給定目標可靠指標下，根據構筑物重要性等級可以校準安全系數。一次逆可靠性法[1-2]（inverse FORM）是目前解決逆可靠性問題的常用方法，在一次二階矩法[3]的基礎上發展而來。Der Kiureghian等[1]給出了逆可靠性算法的迭代公式，Li等[2]將該算法推廣至多個設計參數的情況。

學者們對逆可靠性算法在工程中的應用進行了探討。姬建等[4-5]基于一次逆可靠性法對多種土工構筑物（土質邊坡、條形淺基礎、淺埋圓形隧道）進行概率優化計算。蔣水華等[6]基于一次逆可靠性算法，對土坡坡角進行了分析。Winterstein等[7]基于一次逆可靠性法原理，建立了環境等值線法，著重分析了概率密度等值線（Probability Density Contour，PDC）并用于描述極端結構響應，奠定了一次逆可靠性分析的特殊地位。目前，環境等值線法多應用于海洋工程的逆可靠性分析中。Zhao等[8]將該算法用于推求與目標重現期相應的海洋浮式結構物的設計荷載。而環境等值線法在巖土工程中的應用尚未見報道。為了更直觀地定義與求解可靠指標，吳興征等[9-10]在隨機變量原始物理空間下構建了幾何可靠性算法，將發散概率密度等值面與單倍標準差概率密度等值面之間的相對關系定義為可靠指標，稱為幾何可靠指標。此指標在原理上與常規的可靠指標定義無異，區別在于求解的算法，主要表現在：1）幾何可靠性算法構建于具有明確物理意義的空間內，無需對隨機變量進行標準化處理；2）因采用一系列離散點近似表述概率密度等值線（PDC），幾何可靠性算法對任意非正態聯合分布均適用；3）幾何可靠性算法將常規可靠性尋優求解的過程替換為PDC的幾何演化，使求解過程更簡明。

筆者將幾何可靠性算法與極限狀態分析相結合來構建逆可靠性求解模型，并應用于土工構筑物的承載性能評估。以兩變量隨機問題為研究對象，給定目標幾何可靠指標，假定某一隨機變量的均值（或變異系數）為未知，推求出兩個隨機變量的聯合PDC，通過迭代求解出該待定均值（或變異系數）。這種給定幾何可靠指標而推求未知量的算法稱作逆幾何可靠性算法，力求解決實際工程中檢測數據缺失或無法全面給定所有參數的概率密度分布問題。分別以京畿地區3個建筑場地（順義、后沙峪、燕郊上上城）為例，整理相應土工構筑物（灌注樁、抗浮錨桿、CFG樁單樁）的現場荷載-位移測試數據（共697組），采用兩參數回歸形式（冪函數）對每一條荷載-位移曲線測試結果進行擬合。首先，假定冪函數回歸參數間的相關性，采用高斯Copula函數聯合分布模型構建并推求給定目標可靠指標的PDC；然后，結合極限狀態方程推求未知隨機變量的均值（或變異系數）；最后，求解相應可靠指標下構筑物的安全系數。由此可確保在滿足目標可靠指標的前提下，依據構筑物重要等級校正安全系數。

1 逆幾何可靠性算法

土工構筑物安全性評價中，逆幾何可靠性算法基于目標可靠指標求解描述隨機分布函數的待定參數，如正態分布的均值或變異系數，或者其他分布參數。其包括3個構成部分：極限狀態方程與極限狀態線、聯合概率密度函數與PDC、未知參數的推求工況及其求解過程。

1.1 構筑物的極限狀態方程及極限狀態線

正常使用狀態下構筑物的極限狀態方程g可定義[11]為

g=Q_ua-Q_LD （1）

式中：Q_ua為構筑物的容許承載力；Q_LD為施加荷載。當g為負值時，構筑物處于失效狀態。若采用冪函數進行回歸實測得到的荷載-位移（Q-s）曲線，Q_ua表示為

Q_ua=p_1 〖s_a〗^（p_2 ） （2）

式中：p_1、p_2為Q-s曲線由冪函數擬合的回歸參數。其中，p_1為加載系數，為正值，其大小取決于加載水平；p_2為冪指數，為非負值。理論上講，p_2的值應該小于1，對應于Q與s關系呈凸曲線（p_2等于1時，Q與s呈線性關系）。s_a為容許位移值，正常使用極限狀態下該值可預先給定。同一場地下通常得到多條Q-s測試曲線，由于土體側摩阻力及樁端阻力的空間變異性[12-13]，這些曲線的回歸參數間表現出離散性，故將回歸參數集視作隨機變量。

基于傳統安全系數F_s的定義，平均承載能力與平均設計加荷之間的關系可寫為

F_s=Q_ua/Q_LD （3）

一旦定義了隨機變量，基于式（1）的極限狀態方程，根據變動參數法可求出極限狀態線，具體算法參見文獻[10]。

1.2 聯合概率密度函數與PDC

1.2.1 標準正態空間下的聯合PDC

當可靠指標β已知時，以二元隨機變量為例，給出推求隨機變量聯合PDC的方法。在常規一次可靠性算法中，可靠指標β表示標準正態空間（u1-u2）中某一圓形的特定半徑。標準正態分布是以0為均值、以1為標準差的正態分布，u_1、u_2分別為標準正態空間中的隨機變量。若給定目標可靠指標β_t，則可在標準正態空間中確定半徑為β_t的PDC（即概率密度等值圓形），如圖1所示。顯然，β_t值越高，其對應的PDC輪廓也越大。

由此，二元獨立隨機變量U=（u_1，u_2 ）可隨角度θ變換，并表示為

式中：θ為角度，介于0°～360°之間。

依據《中國建筑結構可靠度設計統一標準》（GB 50068—2018）[14]中給定的某一目標可靠指標，如β_t=3.2，在二元標準正態空間中，通過設定不同的角度θ，即可確定與該可靠指標相對應的PDC上的n個點（圖1中以加號“+”示意出20個離散點）。

1.2.2 原始物理空間下的聯合PDC

若已知隨機變量的邊緣分布和相關系數，通過不同的聯合分布模型，構建原始物理空間中隨機變量的PDC，更易被工程技術人員理解。該空間中的所有隨機變量均具有明確的物理意義，可由前述標準正態空間中的PDC通過聯合分布模型變換得到。以采用高斯Copula函數[15]聯合分布模型構建PDC為例進行說明，盡管建議的算法并不局限于此函數。Copula函數又稱為聯結函數，它將邊緣分布函數和依存關系分開考慮，且不要求變量服從同種邊緣分布，具有較強的靈活性。

將標準正態空間中不相關的隨機變量轉換為W空間中相關的隨機變量[16]，表示為

式中：Φ為標準正態分布的累計分布函數；ρ為標準正態空間中隨機變量u_1與u_2之間的相關系數。基于高斯Copula函數變換，可建立式（5）中w_i與u_i的函數關系，其中i=1或2，與此有關的表達式參見附錄。

進而將W空間中相關的隨機變量映射到含有x_1和x_2的原始物理空間X中，表示為

式中：F_i^（-1）為隨機變量累計分布的逆函數。

可見，基于高斯Copula函數的變換模型可以將標準正態空間中相互獨立的隨機變量U=（u_1，u_2 ）轉換為原始物理空間中具有相依關系的隨機變量X=（x_1，x_2 ），此過程要求給定每個隨機變量的邊緣分布及隨機變量間的相關系數。由此，可靠指標給定時可得到原始物理空間中隨機變量的PDC構型，如圖2所示。亦即將標準正態空間中PDC上的n個點通過高斯Copula函數聯合分布模型轉化為原始物理空間中的n個點并連線，當n趨于無限大時，該輪廓線無限接近于β=β_t時實際的PDC形狀（圖2以乘號“×”示意出20個離散點）。這種離散化近似體現了回歸參數可服從任意概率密度分布形式（如參數化或非參數化聯合分布）的靈活性。隨著β_t值的增大，其對應的PDC輪廓逐漸擴張。

1.3 逆可靠性分析步驟與求解工況

給定不同的目標可靠指標，得到擴張程度不同的PDC。由于可靠指標在幾何上度量了回歸參數的聯合PDC與極限狀態線之間的偏差，PDC的擴張最終被極限狀態線限定。此外，PDC的形狀還取決于隨機變量的邊緣分布類型及其分布參數，以及隨機變量間的相關特性。在逆可靠性分析中，可靠指標β_t已知，且隨機變量的分布類型給定，若描述隨機分布的部分參數未知，則可聯合PDC形狀與大小推求得出，由該等值線與極限狀態線的相切位置可得到未知分布參數，此外，可求出構筑物滿足特定性能的安全系數。

逆幾何可靠性算法的具體求解流程如圖3所示，其由3個模塊組成：1）PDC的推求；2）極限狀態線的構建；3）通過幾何演化求解描述隨機變量的未知參數及構筑物的安全系數。

此處PDC與極限狀態線相切位置是通過判斷一個點（位于極限狀態線上）是否在任意多邊形（PDC）內部來進行的。若在R語言中，可通過調用ptinpoly包中的pip2d函數來實現[17]。

在逆可靠性分析中，假定冪函數回歸的2個隨機變量p_1與p_2之間的相關系數ρ已知，且給定目標可靠指標β_t，可存在4種求解工況。

工況1：假定某一隨機變量（p_1或p_2）的概率密度服從正態分布，且給定該分布的變異系數δ（標準差σ與均值μ之比），待求此分布的均值。設定隨機變量的取值范圍為（0，p_（1 max） ）和（0，p_（2 max） ），繪制出給定目標可靠指標的PDC，沿著已知均值線（由大值到小值）進行PDC移動，PDC的形狀與大小將隨著均值的改變而變化，直至找出其與極限狀態線的切點，從而得到待求均值。

工況2：仍假定某一隨機變量（p_1或p_2）的概率密度服從正態分布，且給定該分布的均值，待求此分布的變異系數。變異系數的大小控制著PDC的扁平程度，扁平程度將隨著變異系數的增大（由小值到大值）而改變，直至PDC與極限狀態線相切，得到待求變異系數。

工況3：給定p_1、p_2均服從最優分布，推求構筑物的安全系數F_s。將隨機變量p_1、p_2的均值代入式（3），得到構筑物的安全系數。可見，確定性安全系數的推求并不能考慮到變量的分布類型。這種情況下，仍可繪制出給定目標可靠指標下的PDC，便于直觀地判定其與極限狀態線間的相對距離。

工況4：假定某一隨機變量（p_1或p_2）的概率密度服從非正態分布，且給定該分布的某一模型參數，待求此分布的另一模型參數。給定目標可靠指標，相應PDC的位置與形狀隨著未知模型參數的改變而變化，直至PDC與極限狀態線相切，得到待求模型參數。這與工況1的求解類似，即這里的逆幾何可靠性算法可適用于多種邊緣分布類型。

4種求解工況下隨機變量的已知量與未知量如表1所示。其他求解工況還可以有相關系數ρ未知時的推求等。

2 算例分析

結合北京市建設工程質量第一檢測所地基室完成的京畿地區3個場地（鉆孔灌注樁、錨桿、CFG樁單樁）的荷載-位移測試成果[10，18]進行分析。除非特別說明，計算中目標可靠指標β_t設定為3.2。

2.1 最優邊緣分布與相關系數

各場地下多條荷載-位移曲線各不相同，則冪函數回歸參數p_1（或p_2）組成一個數據集（隨機變量），服從的候選兩參數邊緣分布概型有正態（Normal）、對數正態（Log-normal）、伽瑪（Gamma）、耿貝爾（Gumbel）和威布爾（Weibull）。

各場地下隨機變量的最優邊緣分布可通過Akaike信息準則（Akaike Information Criterion， AIC）[19]判定，是在極大似然估計原理的基礎上提出的一種模型選擇準則，表達式為

AIC=-2ln（L┴? ）+2p （7）

式中：ln（L┴? ）為極大似然函數；p為模型參數個數（此處為2）。當AIC最小時，對應于最優統計模型。

各場地下隨機變量服從的最優邊緣分布類型如表2所示[10]，具體分布參數值在表中括號內給出。隨機變量p_1與p_2之間的相關系數ρ可采用場地水平下的經驗數據，文獻[20]給出了多個場地下的冪函數回歸參數間的ρ，其均值為-0.77。

2.2 灌注樁的PDC

鉆孔灌注樁豎向抗壓承載力檢測項目位于北京市順義區南法信鎮，共完成了23個荷載-位移測試。

假定p_1服從正態分布且變異系數為0.15，但均值未知，而p_2服從表2中的最優分布。通過逆幾何可靠性算法可求出p_1均值為431.03，灌注樁的安全系數為1.47，求解過程中3個PDC的幾何演化如圖4（a）所示。計算開始時，p_1均值可設置為較大值，此時特定可靠指標（β=3.2）下的PDC與極限狀態線仍有相當的距離，隨著均值的減小，PDC將逐漸接近極限狀態線，直至相切。

假如p_2服從正態分布，其變異系數設定為0.15但均值未知，而p_1服從表2中的最優分布。隨著p_2均值的變化（由大值到小值），PDC將演化至與極限狀態線相切，此時的均值即為待求量。求出p_2均值為0.74，灌注樁安全系數為3.02，PDC如圖4（b）所示。

若灌注樁的p_1與p_2均服從正態邊緣分布，且其均值已知，當p_1變異系數未知而p_2變異系數為0.15時，由圖5（a）可知，PDC隨著p_1變異系數的增大而發生幾何構型演化，當PDC與極限狀態線相交時，得到變異系數為0.78。當p_2變異系數未知而p_1變異系數為0.15時，由圖5（b）可知，PDC隨著p_2變異系數的增大而發生形狀改變，進而求出p_2變異系數為0.49。

若p_1和p_2均為已知隨機變量且服從表2中給出的最優分布形式，給定可靠指標β_t下的PDC如圖6所示。此時若將p_1和p_2的均值代入式（3），可求出灌注樁安全系數為3.13。

2.3 錨桿的PDC

抗浮錨桿抗拔承載力檢測項目位于北京市順義區后沙峪村，共完成了620個荷載-位移測試。若p_2服從表2中給出的最優分布，假定p_1服從正態分布，其變異系數為0.15但均值未知，通過逆幾何可靠性算法可求出p_1均值為48.32，抗浮錨桿安全系數為1.72。均值未知的求解過程中部分PDC如圖7（a）所示。若p_1服從表2中給出的最優分布，假定p_2為正態分布，其變異系數為0.15但均值未知，可求出p_2均值為0.85，抗浮錨桿安全系數為1.63。求解過程中的部分PDC如圖7（b）所示。

假定p_1和p_2均為已知隨機變量且服從表2中給出的最優分布時，給定可靠指標β_t下的PDC，如圖8所示，求得相應的抗浮錨桿安全系數為1.28。

2.4 CFG樁單樁的PDC

CFG樁單樁豎向抗壓承載力檢測項目位于河北燕郊上上城，共進行了54個荷載-位移測試。假定p_2服從最優分布，p_1為正態分布但其均值未知時，由逆幾何可靠性算法求出p_1均值為144.35，CFG樁單樁安全系數為1.61。未知均值求解過程中的部分演化PDC如圖9（a）所示。由圖9可見，隨著未知均值的變化，PDC的位置與形狀發生相應改變，直至與極限狀態線接觸。

若p_1服從最優分布，假定p_2服從正態分布但均值未知時，求出p_2均值為0.67，CFG樁單樁安全系數為2.44。未知均值求解過程中的部分演化PDC如圖9（b）所示。

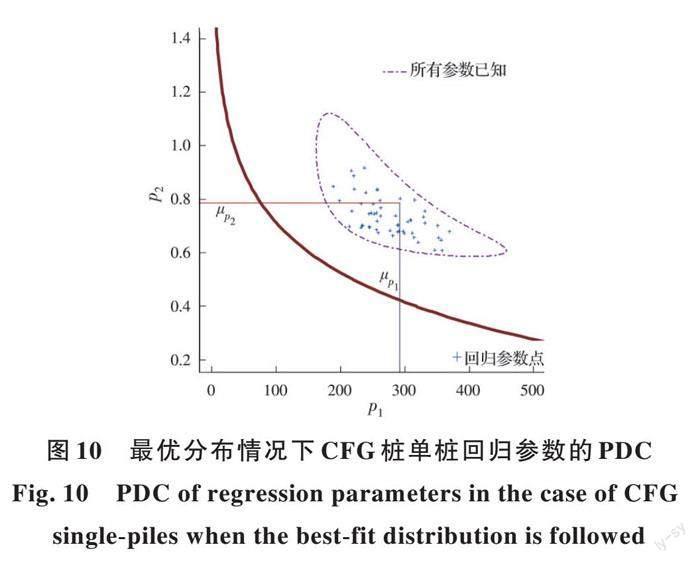
假定p_1和p_2均為已知隨機變量且服從表2中給出的最優分布形式時，給定可靠指標β_t下的PDC，如圖10所示。同樣可求出CFG樁單樁的安全系數為3.98。

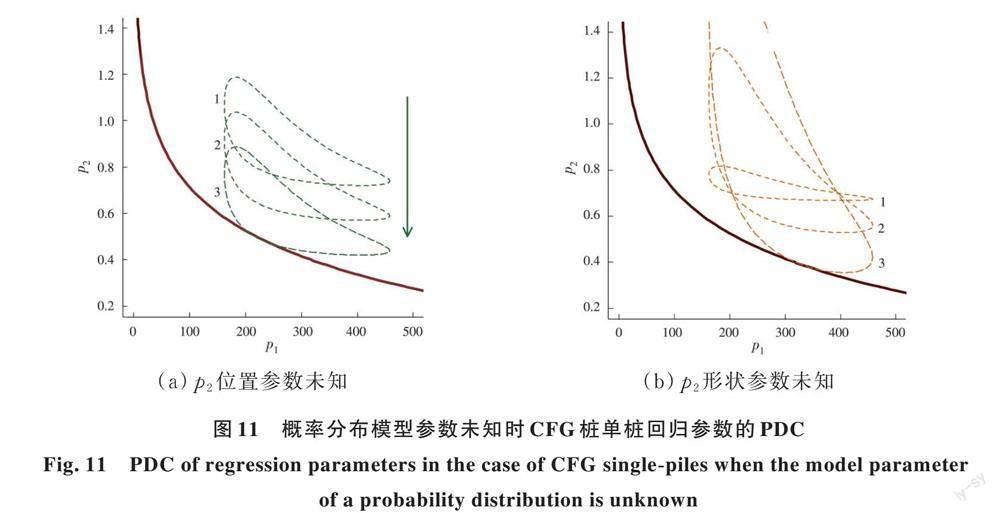
若CFG樁單樁的p_2服從最優邊緣分布，即兩參數Gumbel分布形式，包括位置參數與形狀參數，當p_2的位置參數未知而形狀參數為0.05時，由圖11（a）可知，PDC隨著p_2位置參數的減小而發生幾何構型演化，PDC與極限狀態線相交時得到位置參數為0.52。當p_2的形狀參數未知而位置參數為0.70時，由圖11（b）可知，PDC隨著p_2形狀參數的增大而發生形狀改變，進而求出p_2的形狀參數為0.42。

2.5 算法驗證

以雙變量正態聯合分布為例，選取文獻[10]中由幾何可靠性正分析算法求出的可靠指標與相關系數進行驗證。采用逆幾何可靠性算法求解隨機變量p_1的均值，求得3個場地下p_1均值分別為863.23、36.17、274.11，與文獻[10]給出的隨機變量p_1的實際均值（分別為893.29、36.01、275.94）較為接近。可見，逆幾何可靠性算法在土工構筑物安全性評價中具有一定精度。

該算法基于R語言平臺進行編程實施，可在數秒內完成計算。代碼編寫主要包括：1）由已知量確定聯合分布PDC構型上的離散點，通過未知量的增減實現PDC構型的平移；2）采用等值線Contour函數構建極限狀態線[10]；3）采用pip2d函數進行PDC與極限狀態線相切位置的判定。

3 給定目標可靠指標下各場地的安全系數

根據《建筑結構可靠度設計統一標準》（GB 50068—2018）[14]，不同構筑物等級下發生延性破壞模式時對應的可靠指標β可分別取為2.7（次要）、3.2（一般）、3.7（重要）。分別求解出p_1均值未知（工況1）、p_2均值未知（工況2）、p_1和p_2已知且服從最優分布（工況3）時相應的安全系數，如表3所示。可以看出，隨著目標可靠指標量值的增大，計算得到的安全系數逐漸變大，尤其是p_2均值未知的情況下。應當指出，安全系數由式（3）計算求出，其中Q_ua的值可由p_1和p_2的均值代入式（2）得到。這里的算法使安全系數和可靠指標相互對應，可用于給定目標可靠指標時構筑物安全系數的校正[21]，為建立確定性設計和可靠性設計安全判據的定量關系提供了有效工具。

4 結論

結合京畿地區3個典型場地的荷載-位移測試結果，采用冪函數構建各場地測試曲線的回歸參數集。將回歸參數集視作隨機變量，假定描述隨機變量的某個正態分布參數（均值或變異系數）未知，推求原始物理空間下與目標可靠指標相應的聯合PDC。同時，結合正常使用極限狀態線得到正態分布的未知均值（或變異系數），并求出構筑物的安全系數。將安全系數與可靠指標相結合，根據給定可靠指標即可判斷構筑物的安全性，且充分考慮輸入變量的隨機性，確保構筑物安全。提出的逆幾何可靠性算法對于求解非正態邊緣概率密度分布的未知參數及基于非高斯Copula函數的聯合分布模型變換等情況均適用。對特定案例分別采用幾何可靠性分析的正算法與逆算法得到互為驗證的結果，說明通過逆幾何可靠性算法實現土工構筑物的未知量直觀推求與設計核算是可行的。

基于構筑物施工驗收的荷載-位移檢測結果，建議的逆可靠性方法主要針對設計階段。土工構筑物的極限狀態受到地質條件、物理力學參數、破壞機理、地下水及地震等影響，材料性能劣化或構件性能損傷導致設計基準期內構筑物的抗力發生變化，構筑物在服役期的時變目標可靠指標的確定及逆分析算法有待研究。然而，該算法目前僅局限于低元隨機變量的情況，多元問題的求解有待進一步深入研究。

參考文獻

[1] ?DER KIUREGHIAN A， ZHANG Y， LI C C. Inverse reliability problem [J]. Journal of Engineering Mechanics， 1994， 120（5）： 1154-1159.

[2] ?LI H， FOSCHI R O. An inverse reliability method and its application [J]. Structural Safety， 1998， 20（3）： 257-270.

[3] ?HASOFER A M， LIND N C. Exact and invariant second-moment code format [J]. Journal of the Engineering Mechanics Division， 1974， 100（1）： 111-121.

[4] ?JI J， ZHANG C S， GAO Y F， et al. Reliability-based design for geotechnical engineering： An inverse FORM approach for practice [J]. Computers and Geotechnics， 2019， 111： 22-29.

[5] ?姬建， 張哲銘， 夏嘉誠， 等. 基于逆可靠度分析的隧道開挖面極限支護壓力優化設計[J]. 巖土工程學報， 2021， 43（6）： 1-9.

JI J， ZHANG Z M， XIA J C， et al. Inverse reliability-based design of limit support pressure for tunnel face stability [J]. Chinese Journal of Geotechnical Engineering， 2021， 43（6）：1-9. （in Chinese）

[6] ?蔣水華， 劉賢， 黃發明， 等. 基于一階逆可靠度方法的空間變異土坡坡角設計[J]. 巖土工程學報， 2021， 43（7）： 1245-1252.

JIANG S H， LIU X， HUANG F M， et al. Reliability-based design of slope angles for spatially varying slopes based on inverse first-order reliability method [J]. Chinese Journal of Geotechnical Engineering， 2021， 43（7）： 1245-1252. （in Chinese）

[7] ?WINTERSTEIN S R， UDE T C， CORNELL C A， et al. Environmental parameters for extreme response： Inverse FORM with omission sensitivity[C]//Proceedings of the International Conference on Structural Safety and Reliability， ICOSSAR-93， 1993.

[8] ?ZHAO Y L， LIU D H， DONG S. Estimating design loads with environmental contour approach using copulas for an offshore jacket platform [J]. Journal of Ocean University of China， 2020， 19（5）： 1029-1041.

[9] ?WU X Z. Geometric reliability analysis applied to wave overtopping of sea defences [J]. Ocean Engineering， 2015， 109： 287-297.

[10] ?吳興征， 王瑞凱， 辛軍霞. 特定場地下土工構筑物的幾何可靠性分析[J]. 巖土力學， 2020， 41（6）： 2070-2080.

WU X Z， WANG R K， XIN J X. Geometric reliability analysis of geotechnical structures at a specific site [J]. Rock and Soil Mechanics， 2020， 41（6）： 2070-2080. （in Chinese）

[11] ?辛軍霞， 吳興征， 高偉， 等. 基于Copula函數的CFG樁復合地基載荷-變形曲線的概率分析[J]. 巖土力學， 2016， 37（Sup1）： 424-434.

XIN J X， WU X Z， GAO W， et al. Copula-based analysis of load-displacement curves of cement-fly ash-gravel pile [J]. Rock and Soil Mechanics， 2016， 37（Sup1）： 424-434. （in Chinese）

[12] ?張峰， 周峰， 王旭東. 成層地基中單樁豎向承載力魯棒性設計[J]. 巖土力學， 2017， 38（11）： 3311-3318.

ZHANG F， ZHOU F， WANG X D. Robust geotechnical design of a single pile under vertical loads in layered soils [J]. Rock and Soil Mechanics， 2017， 38（11）： 3311-3318. （in Chinese）

[13] ?TANG C， PHOON K K. Statistics of model factors in reliability-based design of axially loaded driven piles in sand [J]. Canadian Geotechnical Journal， 2018， 55（11）： 1592-1610.

[14] ?建筑結構可靠度設計統一標準：GB 50068—2018 [S]. 北京： 中國建筑工業出版社， 2018.

Unified standard for reliability design of building structures： GB 50068—2018 [S]. Beijing： China Architecture and Building Press， 2018. （in Chinese）

[15] ?NELSEN R B. Archimedean copulas [M]//An Introduction to Copulas. New York： Springer New York， 1999： 89-124.

[16] ?MONTES-ITURRIZAGA R， HEREDIA-ZAVONI E. Environmental contours using copulas [J]. Applied Ocean Research， 2015， 52： 125-139.

[17] ?MAISOG J M， WANG Y， LUTA G， et al. Ptinpoly： Point-in-polyhedron test （2D and 3D） [Z/OL]. R package， version 2.0， 2012. http：//ptinpoly.pbworks.com.

[18] ?吳興征， 王瑞凱， 辛軍霞， 等. 特定場地下土工構筑物荷載變形曲線的概率密度分布[J]. 工程質量， 2017， 35（9）： 41-45， 60.

WU X Z， WANG R K， XIN J X， et al. Probability density distribution of load deformation curves of geotechnical structures at a specific site [J]. Construction Quality， 2017， 35（9）： 41-45， 60. （in Chinese）

[19] ?AKAIKE H. A new look at the statistical model identification [J]. IEEE Transactions on Automatic Control， 1974， 19（6）： 716-723.

[20] ?WU X Z， XIN J X. Probabilistic analysis of site-specific load-displacement behaviour of cement-fly ash-gravel piles [J]. Soils and Foundations， 2019， 59（5）： 1613-1630.

[21] ?陳祖煜. 建立在相對安全率準則基礎上的巖土工程可靠度分析與安全判據[J]. 巖石力學與工程學報， 2018， 37（3）： 521-544.

CHEN Z Y. Reliability analysis and safety criterion in geotechnical engineering based on the index of safety margin [J]. Chinese Journal of Rock Mechanics and Engineering， 2018， 37（3）： 521-544. （in Chinese）

[22] ?ROSENBLATT M. Remarks on a multivariate transformation [J]. The annals of mathematical statistics， 1952， 23（3）： 470-472.

[23] ?WU L. Tuning the bivariate meta-Gaussian distribution conditionally in quantifying precipitation prediction uncertainty [J]. Forecasting， 2020， 2（1）： 1-19.

（編輯 黃廷）

附錄參考文獻：

[1] ROSENBLATT M. Remarks on a multivariate transformation [J]. The annals of mathematical statistics， 1952， 23（3）： 470-472.

[2] NELSEN R B. Archimedean copulas [M]//An Introduction to Copulas. New York： Springer New York， 1999： 89-124.

[3] WU L. Tuning the bivariate meta-Gaussian distribution conditionally in quantifying precipitation prediction uncertainty [J]. Forecasting， 2020， 2（1）： 1-19.