預留土支護基坑旋轉破壞模式下的極限抗力上限解

張輝 吳曙光 楊凱丞

收稿日期：2021?06?13

基金項目：國家重點研發計劃（2018YFC1505501）

作者簡介：張輝（1997- ），男，主要從事巖土工程研究，E-mail：13883690532@163.com。

通信作者：吳曙光（通信作者），男，副教授，E-mail：wushuguang@cqu.edu.cn。

Received： 2021?06?13

Foundation item： The National Key Technologies R&D Program of China （No. 2018YFC1505501）

Author brief： ZHANG Hui （1997- ）， main research interest： geotechnical engineering， E-mail： 13883690532@163.com.

corresponding author：WU Shuguang （corresponding author）， associate professor， E-mail： wushuguang@cqu.edu.cn.

摘要：對于支撐式或錨拉式支擋結構，進行預留土輔助支護時需驗算繞支點的抗傾覆穩定性，然而目前還未找到合理的計算方法。基于極限分析上限定理，提出預留土支護基坑的3種可能破壞模式，運用斜條分法對被動區土體進行離散，并構建相容速度場，分別推導3種破壞模式下基坑抗傾覆力矩的計算表達式，采用遺傳算法編程，分析支擋結構與土體間摩擦系數、土體黏聚力及預留土幾何參數等對破裂角及抗傾覆力矩的影響規律。結果表明：當墻背光滑且土體黏聚力為零時，利用朗肯被動土壓力理論計算得到的抗傾覆力矩為一上限解；存在黏聚力時，朗肯被動土壓力理論計算值偏于保守，存在摩擦系數時，庫倫土壓力理論計算的抗傾覆力矩偏大；與預留土寬度和坡度相比，預留土高度對抗傾覆力矩的影響更加顯著。

關鍵詞：預留土；上限法；極限分析；旋轉破壞；基坑工程

中圖分類號：TU432 ? ? 文獻標志碼：A ? ? 文章編號：2096-6717（2023）05-0116-09

Upper bound solution of ultimate resistance of berm-retained excavations under rotating failure mode

ZHANG Hui， WU Shuguang， YANG Kaicheng

（School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China）

Abstract： For strutted or anchored retaining structures， the anti-overturning stability around the fulcrum needs to be checked for the berm-retained excavations. However， a reasonable calculation method has not yet been found. Based on the upper limit theorem of limit analysis， three possible failure modes of the berm-retained excavations were proposed， the slice method with inclined interfaces was used to separate the passive soil area， and a compatible velocity field was constructed. The expressions for calculating the anti-overturning moment of foundation pit under three failure modes were derived respectively. Through the calculation example， the effects of friction coefficient between retaining structure and soil， soil cohesive force and the berm-retained geometric parameters on the rupture angle and anti-overturning moment were analyzed by using genetic algorithm. The results show that when the wall is smooth and the soil cohesion is zero， the anti-overturning moment calculated by Rankine's passive earth pressure theory is an upper bound solution. When cohesive force exists， the theoretical value of Rankine's passive earth pressure theory is conservative， when friction coefficient exists， the anti-overturning moment calculated by coulomb earth pressure theory is too large. In addition， the berm-retained height has a more significant influence on the anti-overturning moment than the berm-retained width and slope.

Keywords： retained berm； upper bound method； limit analysis； rotational failure； excavation engineering

在基坑施工中，常利用預留土作為支擋結構的臨時支撐，不僅可以有效減小支擋結構的嵌固深度，還能提高支護體系的整體穩定性，在大型基坑中，采用預留土輔助支護可取得較好的經濟效益[1-2]。此外，基坑中經常會因需要容納電梯井、集水井等局部結構而進行二次開挖，形成坑中坑，此時支擋結構與坑中坑之間也可看作是具有一定寬度和高度的預留土臺。

對于錨拉式或支撐式支擋結構，若嵌固深度過小，則會發生繞支點的整體失穩，即旋轉破壞。《建筑基坑支護技術規程》（JGJ120—2012）[3]中對錨拉式或支撐式支擋結構的穩定驗算采用基坑外側主動土壓力相對支點產生的傾覆力矩等于基坑內側被動土壓力產生的抗傾覆力矩的理論，其中土壓力計算一般采用經典朗肯或者庫侖土壓力理論。由于經典朗肯土壓力理論采用半無限土體的假設條件，且兩者均基于平移破壞模式。由于預留土的存在，而基坑被動區土體明顯屬于有限土體范疇，且平移破壞模式的假定也與實際有較大差別。因此，對于預留土支護基坑的穩定性驗算，仍然采用經典朗肯或庫侖土壓力理論并不合適。

近幾十年，許多學者運用不同的方法，包括靜力平衡法[4-5]、多重庫侖楔體分析法[6-7]、彈性抗力法[1-2]、模型試驗法[8]、數值分析法[9-13]、極限分析法[14]等，對預留土的作用機理進行了研究。其中，數值分析法因能模擬較復雜的條件，如多級臺階預留土[15]、不連續預留土的空間效應[16-18]等，故其應用較為廣泛，但計算精度受材料參數和網格尺寸的影響較大；而理論與試驗研究則主要集中在基坑平移破壞模式下預留土對支擋結構內側土壓力大小及分布的影響，這些理論對平移破壞模式下懸臂式支擋結構的設計具有較好的適用性。但在旋轉破壞模式下，錨拉式或支撐式支擋結構的土壓力大小及作用點位置與平移破壞模式下有較大差別[19]，若仍采用平移破壞模式下土壓力大小及作用點位置進行計算，計算結果可靠性得不到保證。

極限分析上限法通過構建機動許可的速度場并運用能量原理求解極限狀態下真解的上限，由于將實際土簡化為理想完全塑性材料，故計算方法簡單、高效。目前，極限分析方法已在邊坡穩定[20-21]、基坑穩定性[22-23]、地基承載力[24]、擋墻地震永久位移及屈服加速度[25-26]等方面得到成功應用，但是將極限分析法應用于基坑旋轉破壞模式下抗傾覆穩定性計算成果相對較少。基于此，將極限分析上限定理和數學規劃法相結合，建立預留土支護基坑3種可能的破壞模式，運用斜條分法對每種破壞模式下預留土支護基坑被動區進行離散，構建相容速度場，得到預留土支護基坑抗傾覆力矩的目標函數。根據算例，采用遺傳算法編程，分析土體參數及預留土幾何參數對破裂角及基坑抗傾覆力矩的影響規律。

1 旋轉破壞模式建立

基本假定：1）墻背豎直，滑裂面為平面；2）墻后土體為可變形體，且與墻體不發生分離；3）土體服從相關聯的流動法則；4）基坑無限長，按平面應變問題分析。

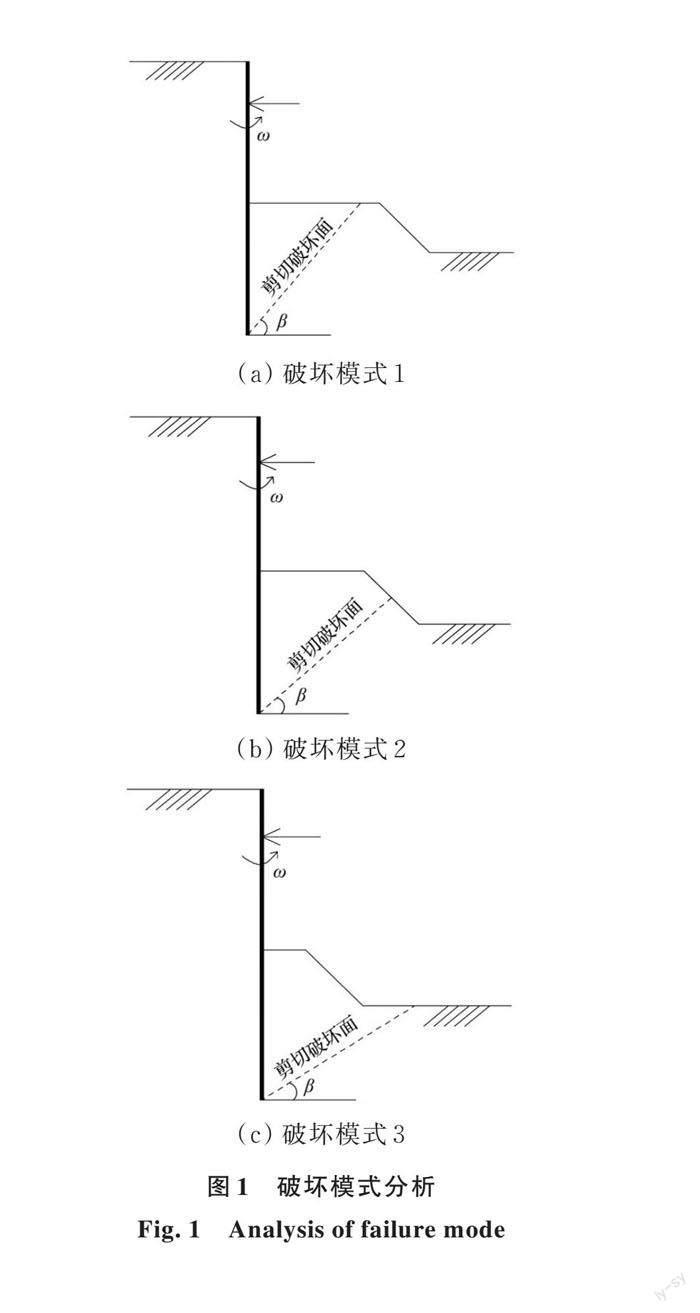
建立3種破壞模式，如圖1所示。當預留土頂部寬度較大時，極限狀態下被動區土體將從預留土頂部剪出；隨著預留土頂部寬度的減小，逐漸轉變成從預留土邊坡和預留土底部剪出。

忽略支擋結構的平動位移，即只考慮繞支點O的轉動，建立如圖2所示的相容速度場，V_oi為墻背點P的速度，V_i為點P處土體以角度β+φ斜向上做直線運動的速度，V_wi為V_oi和V_i的相對速度。φ為土體內摩擦角，ω為支擋結構繞支點O旋轉的角速度，l為支點至點P的距離。

3 參數分析

對于3種破壞模式，均應考慮土體速度方向與水平線夾角在0～π?2，即0<（β+φ）<π?2；考慮垂直擋墻方向外力做功功率與墻背摩擦功率之和大于零，即tan（β+φ）<1?tanδ。另外，如圖6所示，對破壞模式1，還應考慮π?2>β≥β_2；對破壞模式2，應考慮β_2≥β≥β_1；對破壞模式3，應考慮0<β≤β_1。當預留土高度為零時，可視b_f=H?tanβ，此時，破裂角將不受β_1和β_2約束。

對于工程實例，應根據上述約束條件分別計算3種破壞模式的抗傾覆力矩最小值，并以三者中的最小值作為實際的抗傾覆力矩。遺傳算法屬于進化算法的一種，具有良好的全局尋優能力。利用Matlab軟件中遺傳算法工具ga函數來分析土體參數與預留土幾何參數對破裂角及抗傾覆力矩的影響，具體實現步驟為：1）分別將式（19）、式（27）、式（33）創建成函數形式的M文件；2）根據給定參數計算相應的約束條件；3）將3個M文件與對應的約束條件分別帶入Matlab中ga函數，求解出3種破壞模式的抗傾覆力矩M_P，然后取三者中的最小值作為實際的抗傾覆力矩。各參數取值見表1。

3.1 土體參數對β及M_P的影響

對于無預留土的一般基坑，由式（19）可知，抗傾覆力矩M_P是土體力學性質、墻背摩擦系數、支擋結構嵌固深度、基坑底部至支點的長度及破裂角的函數，其一般表達式為M_P=f（γ，c，φ，δ，H，l_0，β）。

3.1.1 c的取值對β及M_P的影響

由圖7可以看出，墻背摩擦系數和土體黏聚力均為0時，利用朗肯被動土壓力理論計算得到的抗傾覆力矩與計算結果相同，說明在此類情況下，利用朗肯被動土壓力理論得到的計算值為一上限解。當黏聚力增大時，計算的抗傾覆力矩增加較朗肯被動土壓力理論計算值更快，原因是該方法在考慮旋轉破壞時假定墻后土體為可變性楔體，土體內部耗能隨黏聚力增大而增大，而朗肯土壓力理論考慮平移破壞模式下墻后土體為剛體，內部沒有能量耗散，故利用平移破壞模式下的朗肯被動土壓力理論計算抗傾覆力矩值偏于保守。另外，該方法計算的破裂角與黏聚力無關，與大主應力面夾角均為π?4-φ?2，與朗肯被動土壓力理論計算的破裂角完全相同。

3.1.2 δ的取值對β及M_P的影響

如圖8所示，墻背摩擦角δ對破裂角的影響較大，破裂角β與墻背摩擦角δ近似呈線性關系，隨著δ從0逐漸增加到30°，β逐漸減小。對于同一摩擦系數，c越大，則β也越大。c=0時，計算得到的破裂角與庫侖被動土壓力理論得到的完全一致。

由圖9可以看出，M_P與δ呈明顯的非線性關系，在c一定時，隨著δ從0逐漸增加到30°，M_P逐漸增大，且變化幅度也增大。當δ與c均為0時，庫倫土壓力理論計算的M_P與本文方法一致，說明庫倫土壓力理論計算的旋轉破壞模式下抗傾覆力矩為一上限解。當墻背存在摩擦角δ時，由庫侖土壓力理論計算得到的M_P大于本文方法計算值，且δ越大，偏差越大。

3.2 預留土幾何參數影響分析

3.2.1 b_f、h_f的取值對β及M_P的影響

由圖10、圖11可以看出，預留土高度h_f為某一定值時，預留土寬度b_f與β和M_P近似呈線性關系，隨著b_f的增加，β遞減，M_P遞增；b_f存在一臨界值，當達到臨界值后，會突變為破壞模式1，此時β及M_P均由破壞模式1確定；預留土高度h_f越大，臨界寬度越大，且M_P的增加幅度也越大；由曲線可以看出，相比增加單位預留土頂部寬度，增加單位預留土高度對M_P的提高更為有效，且預留土頂部寬度越大，提高效果越顯著。

3.2.2 m、h_f的取值對β及M_P的影響

如圖12、圖13所示，對于一定的預留土頂部寬度b_f和高度h_f，在預留土邊坡坡度m較小時，以破壞模式3發生破壞，此時破裂角β隨著m的增加近似呈線性減小，M_p近似呈線性增加，隨著m繼續增大，逐漸轉變成破壞模式2，此時β和M_P均呈非線性增加，且增加幅度逐漸減小，當坡度趨近于無窮時，可看作按破壞模式1破壞；對于不同的預留土高度，當坡度超過一定值后，破裂角幾乎不受坡度影響，且最終均趨近于破壞模式1所確定的破裂角（0.42 rad）；預留土高度越高，坡度對M_P的影響越顯著。

4 案例計算

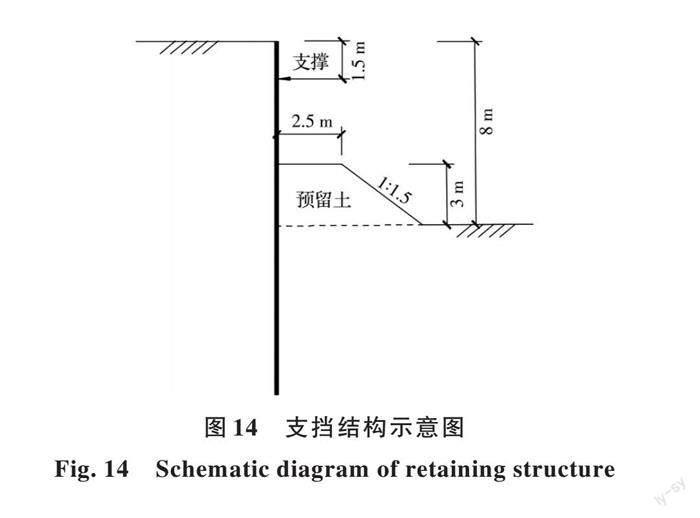
某基坑工程支擋結構形式如圖14所示，樁長17 m，基坑深8 m，支撐距地表1.5 m，基坑內預留土臺進行臨時加強，預留土頂部寬度2.5 m，高3 m，按照1：1.5進行放坡。均質土重度γ為18 kN/m3，黏聚力c為10 kPa，內摩擦角φ為（π?18）rad。

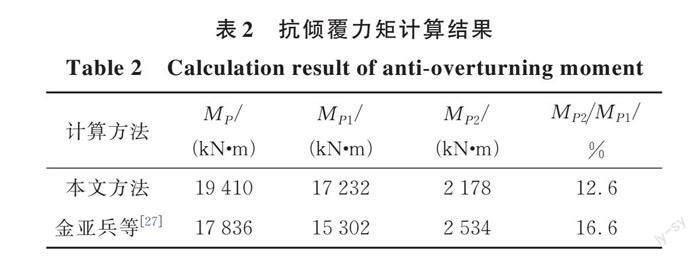
分別采用金亞兵等[27]提出的附加荷載法和本文方法進行計算，結果見表2，其中，M_P表示總的抗傾覆力矩，M_P1為不考慮預留土時基坑提供的抗傾覆力矩，M_P2為預留土提供的抗傾覆力矩。

本文方法計算得到的總抗傾覆力矩大于金亞兵法計算值，但預留土對抗傾覆力矩的貢獻則略小。金亞兵等[27]將預留土與基坑土體分開進行計算，通過附加荷載的方式考慮預留土的作用，本文方法則將預留土與基坑土體作為整體進行分析，更接近于土體實際性狀。

5 結論

1）基于極限分析上限定理直接推導了預留土支護基坑旋轉破壞模式下抗傾覆力矩M_P的表達式，而無需確定被動土壓力的大小和分布，計算上具有一定的簡潔性。

2）對于無預留土的一般基坑，當墻背光滑且土體黏聚力為零時，利用朗肯和庫侖被動土壓力理論計算得到的抗傾覆力矩值均為一上限解。當存在黏聚力時，朗肯土壓力理論計算值偏于保守；當存在墻背摩擦系數時，庫倫土壓力理論計算的抗傾覆力矩偏大。

3）預留土寬度b_f存在一臨界值，當達到臨界值后，會突變為破壞模式1，此時β及M_P均由破壞模式1確定，且預留土高度h_f越大，臨界寬度越大，另外，相比預留土寬度和坡度，預留土高度對抗傾覆力矩的影響更加顯著。

參考文獻

[1] ?李順群， 鄭剛， 王英紅. 反壓土對懸臂式支護結構嵌固深度的影響研究[J]. 巖土力學， 2011， 32（11）： 3427-3431， 3436.

LI S Q， ZHENG G， WANG Y H. Influence of earth berm on embedment depth of cantilever retaining structure for pit excavation [J]. Rock and Soil Mechanics， 2011， 32（11）： 3427-3431， 3436. （in Chinese）

[2] ?鄭剛， 陳紅慶， 雷揚， 等. 基坑開挖反壓土作用機制及其簡化分析方法研究[J]. 巖土力學， 2007， 28（6）： 1161-1166.

ZHENG G， CHEN H Q， LEI Y， et al. A study of mechanism of earth berm and simplified analysis method for excavation [J]. Rock and Soil Mechanics， 2007， 28（6）： 1161-1166. （in Chinese）

[3] ?建筑基坑支護技術規程： JGJ 120—2012 [S]. 北京： 中國建筑工業出版社， 2012.

Technical specification for retaining and protection of building foundation excavations： JGJ 120—2012 [S]. Beijing： China Architecture & Building Press， 2012. （in Chinese）

[4] ?韓同春， 謝靈翔， 劉振. 坑中坑條件下基坑有限土體的被動土壓力計算[J]. 巖土力學， 2018， 39（12）： 4404-4412.

HAN T C， XIE L X， LIU Z. Calculation of passive earth pressure for finite soil in foundation pit under pit-in-pit condition [J]. Rock and Soil Mechanics， 2018， 39（12）： 4404-4412. （in Chinese）

[5] ?陳富強， 楊光華， 孫樹楷， 等. 考慮基坑坑內反壓土作用的實用方法及應用[J]. 地下空間與工程學報， 2019， 15（Sup1）： 299-304.

CHEN F Q， YANG G H， SUN S K， et al. A practical method and engineering application considering the effect of earth berm in foundation pits [J]. Chinese Journal of Underground Space and Engineering， 2019， 15（Sup1）： 299-304. （in Chinese）

[6] ?SMETHURST J A， POWRIE W. Effective-stress analysis of berm-supported retaining walls [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering， 2008， 161（1）： 39-48.

[7] ?DALY M P， POWRIE W. Undrained analysis of earth berms as temporary supports for embedded retaining walls [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering， 2001， 149（4）： 237-248.

[8] ?POWRIE W， DALY M P. Centrifuge model tests on embedded retaining walls supported by earth berms [J]. Géotechnique， 2002， 52（2）： 89-106.

[9] ?陳福全， 吳國榮， 劉毓氚. 基坑內預留土堤對基坑性狀的影響分析[J]. 巖土工程學報， 2006， 28（Sup1）： 1470-1474.

CHEN F Q， WU G R， LIU Y C. Effect of berms on behaviors of excavation supported by sheet-pile walls [J]. Chinese Journal of Geotechnical Engineering， 2006， 28（Sup1）： 1470-1474. （in Chinese）

[10] ?尹盛斌. 基坑預留土臺的簡化分析方法研究[J]. 巖土力學， 2016， 37（2）： 524-536.

YIN S B. A simplified analysis method for earth berm in foundation pit [J]. Rock and Soil Mechanics， 2016， 37（2）： 524-536. （in Chinese）

[11] ?劉暢， 孫盼盼， 趙露偉， 等. 基坑開挖反壓土截面特性對基坑性狀影響的有限元分析[J]. 地下空間與工程學報， 2017， 13（3）： 788-795.

LIU C， SUN P P， ZHAO L W， et al. Finite element analysis of earth berm wxcavation pit traits affect section properties [J]. Chinese Journal of Underground Space and Engineering， 2017， 13（3）： 788-795. （in Chinese）

[12] ?FAN J L， REN Y H， WU Y H， et al. Application of earth berm in foundation pit engineering [J]. Applied Mechanics and Materials， 2014， 638/639/640： 389-392.

[13] ?LEE M H， KIM T H. Parametric study on displacement of earth retaining wall by the bermed excavation using back analysis [J]. Journal of the Korean Geosynthetic Society， 2015， 14（4）： 23-33.

[14] ?秦會來， 周予啟， 黃茂松， 等. 基于上限理論的預留土支護基坑極限抗力分析[J]. 巖土工程學報， 2020， 42（6）： 1101-1107.

QIN H L， ZHOU Y Q， HUANG M S， et al. Passive earth pressure analysis of berm-retained excavation by upper bound method [J]. Chinese Journal of Geotechnical Engineering， 2020， 42（6）： 1101-1107. （in Chinese）

[15] ?ZHANG G， NIE D Q， DIAO Yet al. Numerical and experimental study of multi-bench retained excavations[J]. Geomechanics and Engineering， 2017， 13（5）： 715-742.

[16] ?GOURVENEC S M， POWRIE W. Three-dimensional finite element analyses of embedded retaining walls supported by discontinuous earth berms [J]. Canadian Geotechnical Journal， 2000， 37（5）： 1062-1077.

[17] ?EL-SHERBINY M M， EL-SHERBINY R M， EL-MAMLOUK H. Three dimensional effect of grouted discontinuous berms for passive support of diaphragm walls [C]//Grouting 2017. Honolulu， Hawaii. Reston， VA： American Society of Civil Engineers， 2017： 571-583.

[18] ?EL-SHERBINY M M， EL-SHERBINY R M， EL-MAMLOUK H H. Three dimensional analysis of diaphragm walls supported by passive berms [C]//Engineering Challenges for Sustainable Underground Use， 2018： 115-127.

[19] ?FANG Y S， CHEN T J， WU B F. Passive earth pressures with various wall movements [J]. Journal of Geotechnical Engineering， 1994， 120（8）： 1307-1323.

[20] ?夏元友， 陳春舒. 考慮土體多參數非均質性及各向異性錨固邊坡抗震穩定性極限分析[J]. 巖石力學與工程學報， 2018， 37（4）： 829-837.

XIA Y Y， CHEN C S. Seismic stability limit analysis of reinforced soil slopes with prestressed cables considering inhomogeneity and anisotropy of multiple parameters [J]. Chinese Journal of Rock Mechanics and Engineering， 2018， 37（4）： 829-837. （in Chinese）

[21] ?年廷凱， 劉凱， 黃潤秋， 等. 多階多層復雜邊坡穩定性的通用上限方法[J]. 巖土力學， 2016， 37（3）： 842-849.

NIAN T K， LIU K， HUANG R Q， et al. A generalized upper-bound limit analysis approach for stability analysis of complex multistep and multilayer slopes [J]. Rock and Soil Mechanics， 2016， 37（3）： 842-849. （in Chinese）

[22] ?洪利， 仉文崗. 漸近搜索算法在軟土基坑基底抗隆起上限分析中的應用[J]. 土木與環境工程學報（中英文）， 2020， 42（6）： 46-53.

HONG L， ZHANG W G. Application of progressive search algorithm in upper bound analysis of basal stability for braced excavations in soft clay [J]. Journal of Civil and Environmental Engineering， 2020， 42（6）： 46-53. （in Chinese）

[23] ?李澤， 胡政， 彭普， 等. 基坑穩定性的塑性極限分析上限法研究[J]. 水資源與水工程學報， 2019， 30（3）： 230-236.

LI Z， HU Z， PENG P， et al. Research on upper bound method of plastic limit analysis for excavation stability [J]. Journal of Water Resources and Water Engineering， 2019， 30（3）： 230-236. （in Chinese）

[24] ?瑜璐， 楊慶， 張金利. 基于上限法分析橢圓形結構的極限承載力[J]. 巖土工程學報， 2021， 43（2）： 356-364.

YU L， YANG Q， ZHANG J L. Ultimate bearing capacity of elliptical tip by upper bound analysis [J]. Chinese Journal of Geotechnical Engineering， 2021， 43（2）： 356-364. （in Chinese）

[25] ?王桂林， 趙飛， 張永興. 重力式擋土墻地震旋轉位移下的屈服加速度[J]. 巖土力學， 2013， 34（6）： 1579-1585.

WANG G L， ZHAO F， ZHANG Y X. Earthquake yield acceleration of seismic rotational displacement of gravity retaining wall [J]. Rock and Soil Mechanics， 2013， 34（6）： 1579-1585. （in Chinese）

[26] ?李志浩， 肖世國. 不同運動模式的懸臂式擋墻地震永久位移算法[J]. 巖土力學， 2021， 42（3）： 723-734.

LI Z H， XIAO S G. Calculation method for seismic permanent displacement of cantilever retaining walls considering different movement modes [J]. Rock and Soil Mechanics， 2021， 42（3）： 723-734. （in Chinese）

[27] ?金亞兵， 周志雄. 擋土墻（樁）前堆載反壓或預留土體分析與計算[J]. 巖土力學， 1999， 20（3）： 56-60， 65.

JIN Y B， ZHOU Z X. Analysis and calculation method of surcharge reaction and remaining soils near retaining wall [J]. Rock and Soil Mechanics， 1999， 20（3）： 56-60， 65. （in Chinese）

（編輯 ?胡玲）