計算軸線擺度的公式法
李建民,李正才
(水利部海委引灤工程管理局,河北 唐山 064309)
1 概述
對于立式水輪發電機組,轉動部分的幾何中心線為機組軸線,簡稱軸線,主要包括水輪機軸線與發電機軸線,實際軸線是一條折線,且發電機軸線與鏡板摩擦面不垂直。機組固定部分的幾何中心線稱為機組中心線,理想的機組中心線是一條鉛垂線。過鏡板摩擦面中心點的鏡板摩擦面的法線為旋轉中心線[1]。
在機組運行過程中,軸線上某點在某個方向偏離機組中心線的量稱為在該方向的運行擺度。在盤車過程中,軸線上某點在某個方向偏離旋轉中心線的量稱為該方向的盤車擺度,以下所述擺度指盤車擺度[2]。
軸線的測量與調整是水輪發電機組的安裝[3]和檢修中的一項重要內容,一般均分8 個軸號,通過等角盤車法測量軸線擺度,在剛性盤車過程中,鏡板摩擦面可以傾斜但沒有水平變化,假設旋轉軸沒有徑向位移,軸線上任何一點的運動軌跡都是一個標準圓,稱之為擺度圓。彈性盤車時,鏡板摩擦面的水平可能產生細微變化,可以精確測量并參與擺度計算,傳統做法是盡量監測控制鏡板水平變化,不參與擺度計算。
盤車后,先計算出目標位置如水導處的百分表讀數,減去基準位置如發電機導軸承處的同方位百分表讀數,一般稱該差值為凈擺度,從嚴格意義上講,這是錯誤的,為了方便起見,下面仍沿用該錯誤叫法。計算出所有方位的凈擺度后再繪制擺度曲線:以軸號為橫坐標,凈擺度為縱坐標,標記所有盤車點,依次光滑連接形成一條近似正弦曲線,稱之為盤車擺度曲線,盤車擺度曲線最高點的橫坐標為最大擺度方位,最高點與最低點的縱坐標之差為擺度圓直徑。擺度曲線完全等效于一個近似圓,稱之為盤車擺度圓,由于擺度圓是軸線上某點的運動軌跡,比擺度曲線更直觀反映軸線擺度,判斷盤車擺度圓是否接近標準圓比判斷盤車擺度曲線是否接近標準正弦曲線也更簡單直觀。
2 擬合擺度圓
如圖1,取測量位置如水導或法蘭處的軸的橫斷面作為研究對象,實線圓為軸的理想位置,軸表面上的M 點位于基準方位即0°方位,軸表面上某點與M 點形成的圓心角稱為該點的方位角,即該點位于所述角度的方位,方位角按俯視逆時針方向遞增,方位是基于旋轉軸而言,軸表面上的N 點朝向最大擺度方位,軸心的實際位置朝該方位的偏移量為擺度圓半徑。

圖1 測點關系示意圖
在x方向與y方向架設百分表測量擺度,當ωi方位朝向x方向時停止盤車,讀取各百分表的讀數,記其凈擺度分別為xi、yi,此時,坐標系原點O 點位于旋轉中心線上,軸心實際位置P 是虛線圓弧的圓心,由于軸半徑R遠遠大于擺度圓半徑r,可知有向線段:
絕對精確的凈擺度(x,y)反映P 的實際位置,即:
其中a、b為常數,與測量方位無關,與百分表對0 有關,這也是xi、yi不能稱為嚴格意義上的凈擺度的根本原因。由于存在測量誤差,根據凈擺度計算的軸心位置為Q,將所有點(xi,yi)(i=1,2,…,k)繪制在一個坐標系中并依次光滑連接形成近似圓,則為實際擺度圓。
下面根據最小二乘法求出一個滿足⑴式的最接近實際擺度圓的標準圓,稱為擬合擺度圓。分析處理測量誤差,記:
(rsin(θ-ωi)+b-yi)2達到最小
可求得:
在0°~360°范圍內,存在兩個θ 值滿足⑵式,其中一個使r為正,另一個使r為負,取前者。當k=2t且測點勻布時,m=n=0,編號2t相當于軸號0,規定為基準方位。
下面舉例說明利用擺度圓分析處理盤車記錄的完整流程。
潘家口水電廠位于河北省遷西縣境內,裝有一臺150 MW 機組。2008 年擴修時進行了彈性盤車,分10 個軸號,其編號記為0~9,俯視逆時針遞增,以軸號0 為基準方位。在X 方向與Y 方向各設一組百分表測量軸線擺度,各軸號轉至X 方向時,記錄各百分表讀數。
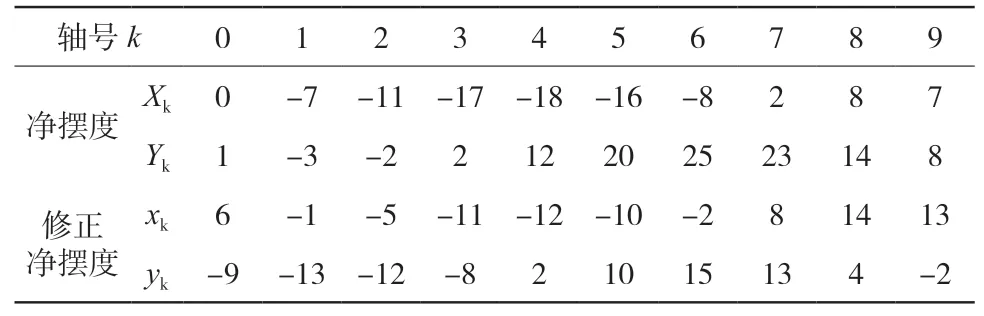
表1 水導處基于發電機導軸承的凈擺度單位:0.01 mm
修正擺度值可使(1)式中a=b=0,對稱軸號處的修正凈擺度應為相反數,依此可簡單判斷盤車是否成功,這是判斷盤車精度的必要但非充分條件。將(xi,yi)(i=0,1,2,…,9)繪制在坐標系中并依次光滑連接,得到實際擺度圓即圖2,近似反映了水導處的軸心運動軌跡,選取適中半徑如r=13.5 為擺度圓半徑,根據(1)式可知,最大擺度方位朝向圖2 的x方向即軸號8 偏9 大約20°,θ=8×36°+20°=308°,可根據擺度圓參數及最終停軸位置分配水導瓦間隙。
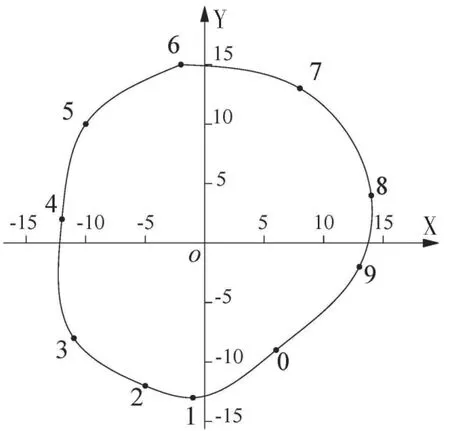
圖2 擺度圓
圖2中圓點編號的含義:當相應軸號朝向X 方向時,測量得到的水導處軸心位置。軸號按逆時針方向遞增而圓點編號按順時針方向遞增的原因在于:在圖1 中,∠CON 與ω1的遞增方向相反,(1)式也可體現。
根據(2)、(3)式可求得擬合圓參數:θ=312°,r=13.4,這是最接近實際擺度圓的標準圓,與實際擺度圓參數基本吻合。分配水導瓦間隙時,宜優先依據擬合擺度圓。
3 擬合擺度曲線
前面介紹了在互成90°的正交方向測量擺度從而求出擬合擺度圓的方法,單方向測量擺度,可繪制出實際擺度曲線,是一條近似正弦曲線,也可求出最接近實際擺度曲線的標準正弦曲線即擬合擺度曲線,擬合擺度曲線的一般表達式:
求出r,φ,t,可自然生成擬合擺度圓:
其中s可為任意常數,因此,任何擬合擺度曲線都等效于某個擬合擺度圓,擬合擺度曲線與擬合擺度圓在本質上相同,其根本目的是確定擺度圓半徑與最大擺度方位。
下面給出由一組測量值(ωi,yi)(i=1,2,…,k)確定的(4)式擬合擺度曲線:
當k為偶數且測點均布時,m=n=p=q=0。
這是太平灣電廠提及的多點任意角盤車的擺度計算公式,太平灣電廠未給出該公式,由電腦近似處理,為此開發相應軟件實無必要,其計算精度也不及上述公式。
4 總結
擺度圓處理方法適合互成90°正交測量盤車擺度,比擺度曲線直觀精確,消除了人為的誤差。給出了正交測量的擬合擺度圓及單方向測量的擬合擺度曲線的計算公式,減小了確定擺度圓半徑及最大擺度方位的主觀性,為處理機組軸線及分配軸瓦間隙提供更精確的理論依據。采用偶數點等角盤車,計算擺圓半徑及最大擺度方位的公式并不復雜,實用性比較強。

