基于關鍵翻轉集合的極化碼Fast-SSC-Flip譯碼算法

郭 銳 孫 荷 楊 沛

(杭州電子科技大學通信工程學院 杭州 310018)

1 引言

極化碼是目前唯一一種通過理論證明能夠達到香農極限的信道編碼方案[1]。由于極化碼具有低復雜度的編譯碼結構和優良的糾錯性能，其已成為5G增強移動寬帶場景(Enhance M ob ile B road Band,EM BB)中控制信道的編碼方案。當極化碼的碼長趨近于無窮大時，串行抵消譯碼算法(Successive Cancellation,SC)被證明是一種可使極化碼的糾錯性能達到信道容量的譯碼算法。但SC譯碼算法在有限碼長情況下的譯碼性能并不理想，并且具有較高的譯碼時延。

為此，研究者提出了串行抵消翻轉(Successive Cancellation Flip,SC-Flip)譯碼算法[2]。該算法在首次SC譯碼失敗后，繼續嘗試多次SC譯碼，選擇易錯的候選比特(Candidate B it,CB)進行翻轉。Chandesris等人[3]提出了一種動態SC-Flip(Dynam ic-SC-Flip,D-SC-Flip)譯碼算法。該算法通過一種新的度量準則來權衡候選比特的譯碼順序和決策對數似然比(Log-Likelihood Ratio,LLR)對候選比特可靠性的影響，動態構建及更新候選翻轉比特集合，同時翻轉多位錯誤比特。文獻[4]通過比較LLR計算得到的錯誤概率與高斯近似(Gaussian Approximation,GA)計算得到的錯誤概率，以此來縮小D-SC-Flip譯碼算法的候選翻轉比特集合。文獻[5]通過優化候選翻轉集合的構造，減少D-SC-Flip譯碼算法的搜索復雜度。文獻[6]提出了基于門限的候選翻轉集合構造算法，進一步提升了譯碼性能。文獻[7]提出了一種新型的SC-Flip譯碼算法，同時利用奇偶校驗(Parity Check,PC)和循環冗余校驗(Cyclic Redundancy Check,CRC)的校驗作用，相比于CRC輔助的SC-Flip譯碼算法，獲得了更好的性能和復雜度的折中。

為了降低SC算法的譯碼時延，文獻[8]提出了簡化的SC(Sim p lified SC,SSC)譯碼算法。SSC譯碼算法能夠在Rate0節點以及Rate1節點直接進行硬判決譯碼，有效地降低了譯碼時延。隨后，Sarkis等人[9]進一步提出了單奇偶校驗(Sing le Parity Check,SPC)以及重復(REPetition,REP)節點，并提供了這兩種特殊節點的直接譯碼方法，使得改進后的快速簡化串行抵消(Fast-Sim p lified Successive Cancellation,Fast-SSC)譯碼算法相較于SC譯碼算法在不損失糾錯性能的前提下極大地降低譯碼時延。進一步地，文獻[10]對Fast-SSC譯碼算法中的各種特殊節點做了歸納總結，提出了更具一般性的Type-I,Type-II,Type-III,Type-IV以及Type-V節點，通過對這5種節點直接譯碼，從而極大地改善SC譯碼算法的譯碼時延。

Giard等人[11]將Fast-SSC譯碼算法與SC-Flip譯碼算法相結合，提出了Fast-SSC-F lip譯碼算法。Fast-SSC-Flip譯碼算法允許在初始Fast-SSC譯碼失敗之后，繼續嘗試執行最多Tmax次Fast-SSC譯碼算法，且每次執行Fast-SSC譯碼時選擇候選翻轉比特集合中的某個比特進行翻轉。然而傳統Fast-SSC-Flip譯碼算法在對SPC節點進行翻轉譯碼時會有輕微的性能損失，為此研究者提出了一種新的Fast-SSC-Flip[12](New-Fast-SSC-Flip,N-Fast-SSCF lip)譯碼算法，能取得優異的譯碼性能。同一作者在文獻[13]中提出了一種適用于衡量Fast-SSC譯碼過程中候選比特可靠性的度量準則，該度量準則能夠更精確地定位到首位譯碼錯誤比特。文獻[14]提出了基于易錯比特列表和分段CRC校驗的Fast-SSC-F lip譯碼算法，進一步提升譯碼性能。文獻[15,16]提出了兩種增強型的多比特翻轉Fast-SSC譯碼算法來糾正Fast-SSC譯碼過程中的多位譯碼錯誤比特。

候選翻轉比特集合是影響Fast-SSC-Flip算法譯碼復雜度以及譯碼性能的關鍵因素之一，集合大小影響候選比特的搜索效率以及復雜度。當前Fast-SSC-Flip譯碼算法搜索候選翻轉比特的范圍與全部信息比特構成的集合的維度一致。因此，本文在CS的基礎上提出了關鍵翻轉集合(Critical Flip Set,CFS)，將Fast-SSC-Flip譯碼中候選比特搜索范圍定位到CFS中，并提出了基于CFS的Fast-SSCFlip譯碼算法，從而降低傳統Fast-SSC-Flip譯碼算法的候選翻轉比特集合大小，減小搜索復雜度。

2 Fast-SSC-Flip譯碼算法

2.1 Fast-SSC譯碼算法

圖1 所示的極化碼S C 譯碼樹利用R a t e 0，Rate1，REP以及SPC節點進行剪枝之后，可以得到如圖2所示的Fast-SSC譯碼樹。Fast-SSC譯碼樹相較于最初的SC譯碼樹而言，其高度已經大大降低，因此深度優先遍歷的效率可以得到提升，相應的譯碼時延也會降低。

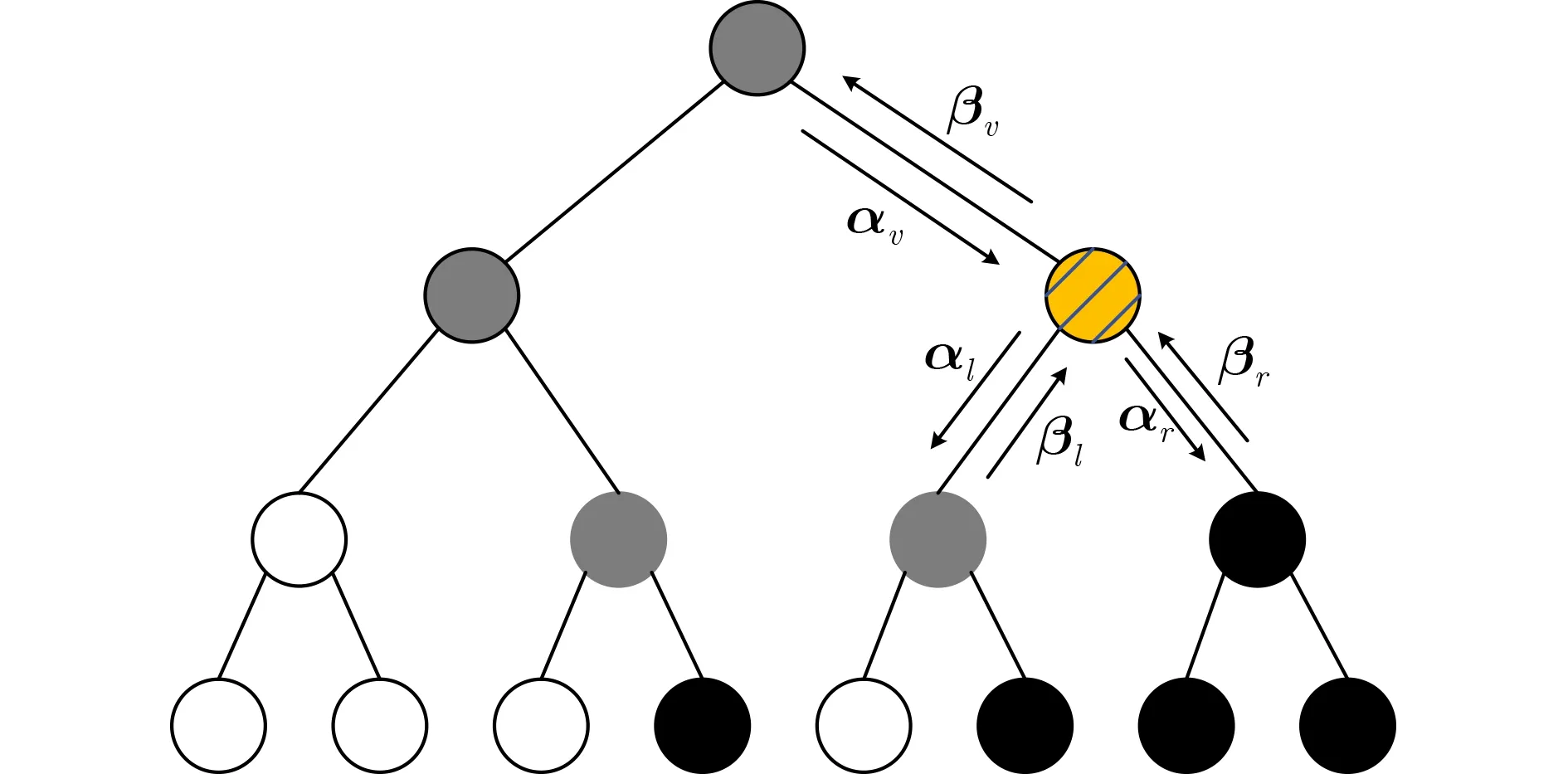
圖1(N,K)=(8,4)的極化碼SC譯碼樹

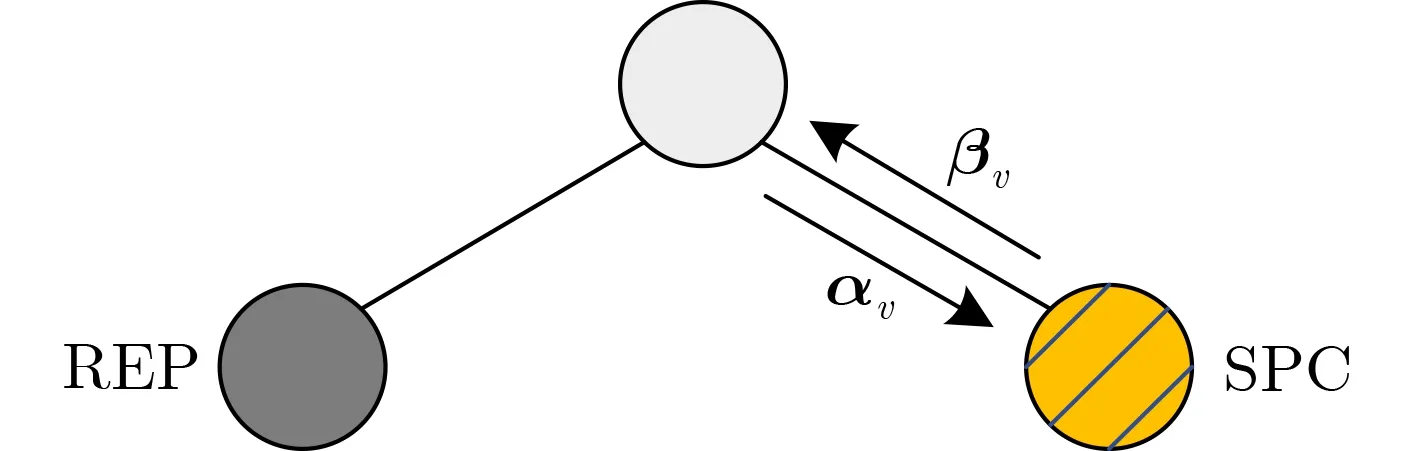
圖2(N,K)=(8,4)的極化碼Fast-SSC譯碼樹

Rate0節點表示該節點有連續 2S個比特為凍結比特，因此將該節點的所有碼字比特硬判決為全0比特；Rate1節點表示該節點有連續 2S個比特為信息比特，在該節點直接利用硬判決方法進行譯碼。REP節點僅僅只有最右側的葉節點是信息比特，而其余的葉節點全是凍結比特。Fast-SSC譯碼算法在REP節點直接利用最大似然譯碼算法進行譯碼。SPC節點是指在以該節點為根節點的譯碼子樹中，只有最左側的葉節點是凍結比特，其余的葉節點全是信息比特。同理，Fast-SSC可以直接在SPC節點進行硬判決(Hard Decision,HD)，譯碼輸出結果為

其中，HD[i]表 示根據SPC節點內的第i個比特的LLR值進行硬判決，判決方式如式(2)所示；p表示SPC節點內所有比特的譯碼估計值的總和，計算方式如式(3)所示；iε表示SPC節點內最不可靠的一位信息位的索引位置，選擇方法如式(4)所示

2.2 Fast-SSC-Flip譯碼算法

Fast-SSC-Flip算法通過找到Fast-SSC譯碼中不可靠的比特加入到候選翻轉比特集合中，并在額外譯碼中嘗試逐次翻轉不可靠的比特，直至譯碼輸出正確結果或者達到設置的最大額外嘗試譯碼次數Tmax。

在衡量Fast-SSC譯碼過程中候選比特可靠性時，需要根據不同節點類型分別計算各個節點內候選比特的可靠性。由于Rate0節點內包含的所有比特全是凍結比特，這些凍結比特在接收端和發送端也被假設是已知的。因此本文在構建候選翻轉比特集合時，僅考慮Rate1，REP以及SPC 3種節點內的信息比特。

Rate1節點內的任意第i個CB的可靠性度量計算方式為

當需要翻轉的比特位于該節點內時，相應位置的比特進行翻轉。

REP節點內僅含有一個信息比特，即在該節點內有且僅有1個CB，且該CB位于末尾位置。該CB的可靠性度量計算方式為

其中，N v表示該節點的長度，即包含凍結比特以及信息比特的總數量。當需要翻轉的比特位于REP節點內時，該節點內的末尾比特進行翻轉。

SPC節點內CB的可靠性度量計算及其無損翻轉譯碼方法為

其中，p以及iε計 算方式參見式(3)和式(4)，ε表示節點內最不可靠的比特的決策LLR值，可用式(8)計算

在Fast-SSC-F lip譯碼算法中，無論是計算候選比特的度量值，還是選擇不可靠的候選比特執行翻轉譯碼，都與候選翻轉比特集合的大小相關。然而大部分現存文獻中的Fast-SSC-Flip算法的候選翻轉比特集合的大小都等于信息比特集合的大小，因此若能有效縮小候選翻轉比特集合的大小，則可以有效減少度量值計算以及排序復雜度，并且可以提升候選比特的搜索效率。為此，本文利用極化碼的生成矩陣得到與CS中信息比特相應的碼字比特，并用這些碼字比特構建關鍵翻轉集合CFS作為候選翻轉比特集合。從而降低Fast-SSC-F lip譯碼算法的候選翻轉比特集合大小，減小搜索復雜度。

3 Fast-SSC譯碼算法中CS構造及其有效性

為了降低Fast-SSC-F lip譯碼算法搜索候選翻轉比特的復雜度，一種直接的思想是縮小譯碼過程中首位錯誤比特的搜索范圍，文獻[16]提出的關鍵集合CS能夠將SC譯碼算法中首位錯誤比特定位到CS中，CS在SC譯碼算法中有極大概率包含首位錯誤比特。然而由于Fast-SSC并不是在SC譯碼樹的葉節點得到譯碼信息比特值，而是在Fast-SSC譯碼樹的各種特殊節點得到相應的碼字比特序列。故本節首先研究了CS在Fast-SSC譯碼算法中的有效性。

3.1 CS構造方法

構建CS的方法簡述為：首先將SC譯碼樹裁剪為SSC譯碼樹，裁剪后的譯碼樹中編碼速率為1的葉節點(等效于Rate1節點)被稱為極化子塊，每個子塊都是一個僅包含信息比特序列的極化碼。將所有子塊中的首位比特依次放入到初始化為空集的CS中完成CS的構建。CS詳細的構建方法如算法1所示。

3.2 CS有效性

本節主要驗證CS集合在Fast-SSC譯碼算法下是否能夠有效地包含Fast-SSC譯碼算法的首位錯誤比特。本節的仿真參數如下：極化碼編碼方式為非系統編碼，接收端采用Fast-SSC譯碼算法。設置極化碼碼長N=1 024，信息比特長度K=512，碼率R=0.5，蒙特卡羅仿真次數為Tsim=106。

仿真結果見表1，“譯碼錯誤幀數”表示采用Fast-SSC譯碼得到的錯誤譯碼總幀數；“首錯在CS中”表示Fast-SSC譯碼中的首位錯誤信息比特在由算法1構造的CS中的總幀數；“準確性”由兩者的比值得到；“CS的維度”表示CS集合的大小。

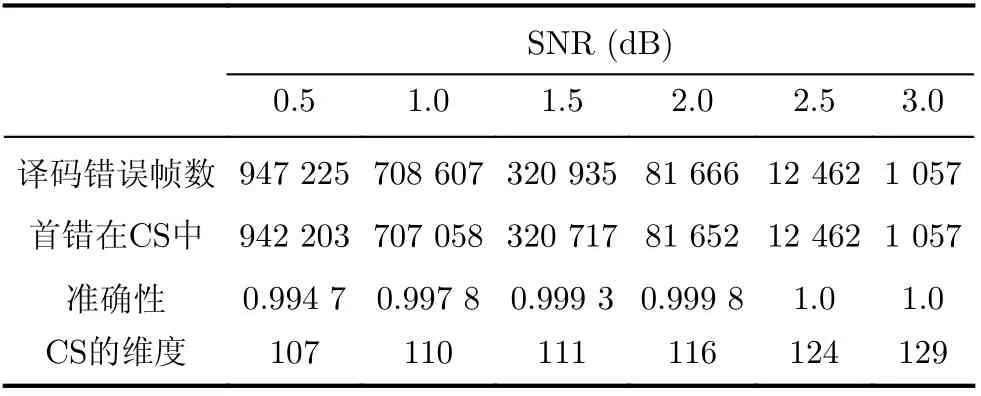
表1 N =1 024, K =512 T sim =106, 時CS的有效性驗證

仿真結果驗證了CS在Fast-SSC譯碼過程中仍然有效，即CS有接近100%的概率能夠包含Fast-SSC譯碼過程中的首位譯碼錯誤比特，且CS的維度小于信息比特集合的大小。

4 關鍵翻轉集合CFS的構造

4.1 基礎理論及結論證明

圖3給出了SC譯碼樹轉換成Fast-SSC譯碼樹的過程。{u1,u2,u3,u5}表 示凍結序列，{u4,u6,u7,u8}表示信息序列。右邊的譯碼樹表示該極化碼的Fast-SSC譯碼樹。其中左邊葉節點為REP節點，該節點可以描述成一個長度為4，包含{u1,u2,u3,u4}的子極化碼。同理，右邊葉節點為SPC節點，可以描述為一個長度為4，包含{u5,u6,u7,u8}的子極化碼。

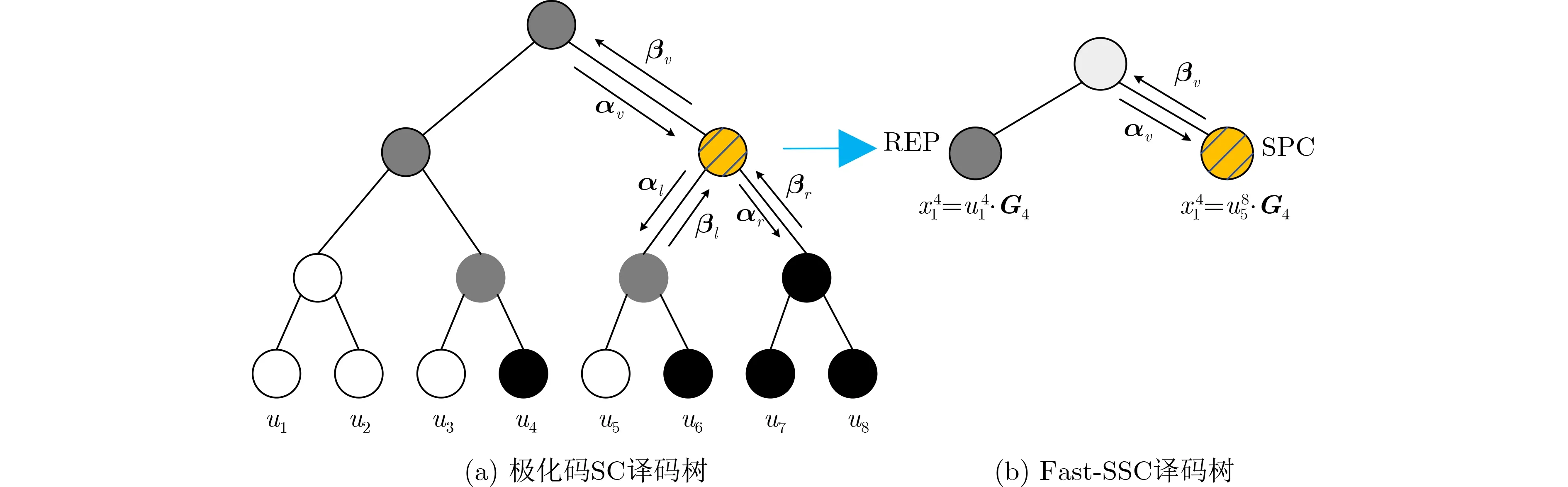
圖3 極化碼SC譯碼樹以及Fast-SSC譯碼樹

當進行Fast-SSC譯碼時，利用硬判決方法對REP以及SPC節點直接譯碼得到的結果稱為碼字序列。在Fast-SSC譯碼過程中，只有翻轉首位錯誤碼字比特才能避免錯誤傳播對Fast-SSC譯碼過程的影響。然而CS是相對于信息比特序列而言的，因此對于Fast-SSC譯碼，需要尋找與CS中的信息比特相應的候選比特(碼字比特)才能構建候選翻轉比特集合。

對于一個碼長為N=2n的極化碼，其生成矩陣G N=(g1,g2,...,g N)=F?n，其中GN的列向量gi中元素1的位置構成的集合為Ωi。若葉節點l長 度為L，當前子極化碼對應于極化碼的索引為(τ+1,τ+2,...,τ+L)，l由包含的信息比特序列經過極化編碼構成，在節點l處可得到碼字序列為

其中，G L為 該子極化碼的生成矩陣。當譯碼樹的葉節點l為Rate1或者REP節點時，在2元域下，本文給出如下命題：

命題1若Fast-SSC譯碼中首位錯誤信息比特uτ+i在 譯碼樹的葉節點l內，且是由l譯碼得到的部分碼字比特x?Φ錯誤導致的，則必然有Φ?Ωi且有極大概率|Φ|=1，其中Φ表示為候選翻轉比特集合。

證明 若節點l得到的譯碼碼字序列為，則該節點包含的信息序列為

其中，第2步等式是根據文獻[1]中給出的G N=，故可以得到首位錯誤比特uτ+i的估計值為

因此對于Rate1及REP節點而言，若確定首位錯誤信息比特uτ+i，則其相應的候選比特集合Φ可由命題1得到。當譯碼樹的葉節點l為SPC節點時，若首位錯誤信息比特uτ+i在該節點內，則根據文獻[17]可知，SPC節點有極大概率僅存在兩位錯誤比特，一位為固定翻轉碼字比特(由于該比特是固定翻轉比特，因此并沒有被包含于該文獻中的節點內錯誤比特數量統計結果)，另一位為待確定的由信道噪聲導致譯碼錯誤的某個候選碼字比特e。由于命題1是在2元域討論下得到的結論，則兩位錯誤比特必然不可能同時在xΩi中，否則根據式(11)可知，兩位錯誤比特將導致uτ+i正確譯碼。將uτ+i相應的固定翻轉位記作με，且計算為

綜上所述，對于Rate1，REP以及SPC 3種特殊節點，若確定首位錯誤信息比特uτ+i，則都能夠利用命題1來構建uτ+i相應的候選比特集合。

為了便于理解命題1，本文以圖2中的SPC節點為例。該SPC節點為一個碼長N=4的子極化碼，包含信息比特序列(u6,u7,u8)，u5為凍結比特且設置為0，該子極化碼對應的子樹結構如圖4所示，其中藍色節點表示SPC節點，白色葉節點表示凍結比特，黑色葉節點表示信息比特。當利用Fast-SSC算法進行譯碼時，在SPC節點得到的正確譯碼碼字為

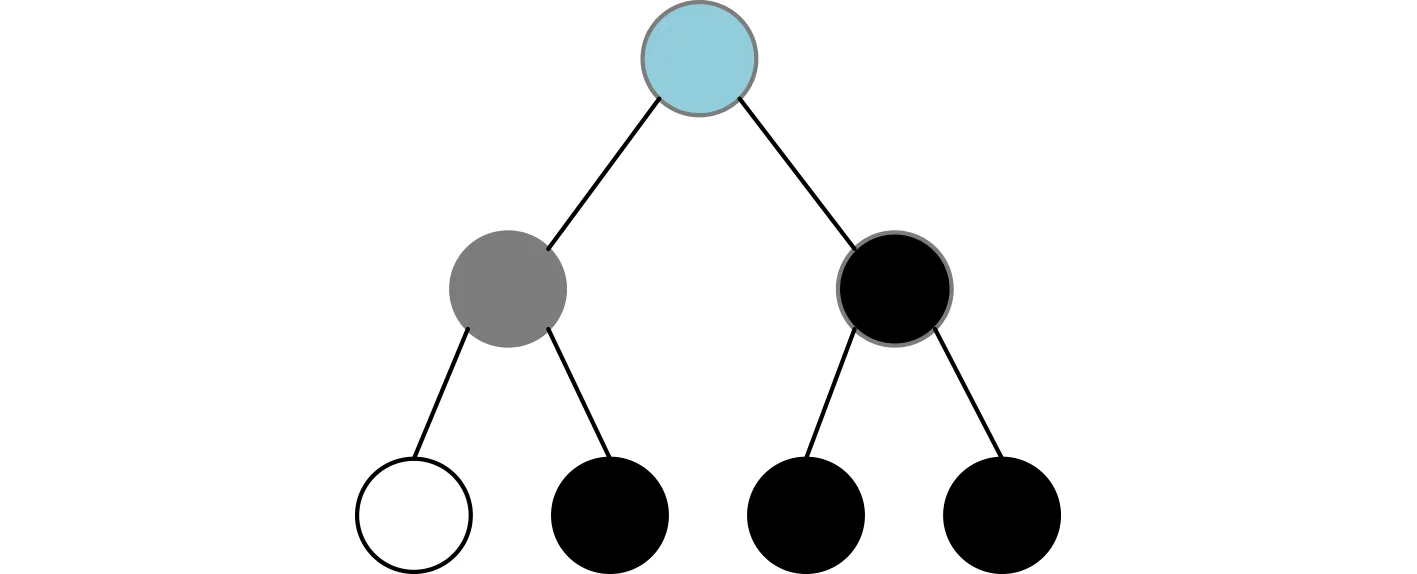
圖4 譯碼樹SPC節點對應子樹結構

其中，G4為該子極化碼的生成矩陣。假設上述的極化碼在Fast-SSC譯碼中首位錯誤比特為u6，則根據式(13)有

根據式(14)可知，導致u6譯碼錯誤的原因是x2或x4譯碼錯誤，即有Φ={2}或Φ={4}；顯然Ω2={2,4}，故Φ?Ωi成立。證畢

4.2 CFS構造算法

基于上述的命題1，在Fast-SSC譯碼過程中，首位錯誤信息比特一般都是由其所在的子極化碼的某位碼字比特xΦ譯碼錯誤導致的；同時根據Fast-SSC譯碼中首位錯誤信息比特有接近100%的概率在CS中的結論，本文將CS中的每個信息比特對應的xΦ收集起來構成一個關鍵翻轉集合CFS。不同于CS的構建方法，CFS在CS的基礎上，需要利用LLR以及生成矩陣完成，其不僅與極化碼的結構有關還與譯碼過程有關。

CFS構建方法如算法2所示：注意到算法2所述算法的第1行利用的是算法1所述的CS構造函數；第3行根據Fast-SSC譯碼樹結構確定CS(i)相應的Ω，先確定C S(i)所 在的子極化碼生成矩陣GN以及其相對節點內的首位信息比特的位置i，根據GN以及i確定相應的Ω；第4行描述的衡量碼字比特可靠性的度量準則，所使用的度量準則為碼字比特的決策LLR。表示碼字比特序列相應的決策LLR向量。

算法2 CFS構造算法

CFS構造算法一個直觀的解釋是，Fast-SSC譯碼過程中首位錯誤比特一般是由于該比特所在的子極化碼某位譯碼錯誤導致的，且該比特必然屬于因此本文選擇xΩ中最不可靠的碼字比特作為CFS集合中的一員。同時，由于CS集合有極大概率包括Fast-SSC譯碼的首位錯誤比特，故為了減少復雜度，本文僅考慮在CS基礎上構建相應的CFS。

5 CFS-Fast-SSC-Flip譯碼算法及性能

5.1 CFS-Fast-SSC-Flip譯碼算法

本文基于提出的CFS設計了一種單比特翻轉Fast-SSC譯碼算法，命名為CFS-Fast-SSC-Flip譯碼算法。CFS-Fast-SSC-Flip譯碼算法詳細的描述見算法3。所提算法與傳統的Fast-SSC-Flip譯碼算法的主要區別為：所提算法選擇候選比特進行翻轉譯碼時僅從CFS中選擇，相較于傳統的Fast-SSCFlip使用整個信息比特集合的搜索范圍而言，減小了搜索復雜度，有效提升候選比特的搜索效率。

5.2 CFS-Fast-SSC-Flip譯碼器性能分析

為了研究提出的CFS-Fast-SSC-Flip譯碼算法譯碼性能，本節將算法3中第4行的度量準則設置為根據候選比特的決策LLR升序排序，并與Fast-SSC-Flip(s=0.5，算法補償系數)，N-Fast-SSCFlip,Fast-SSC以及SSC-Oracle譯碼算法進行性能比較。由于本文所提的CFS-Fast-SSC-Flip譯碼算法的CFS是基于CS構建的，因此本文同時比較了基于CS的Fast-SSC-Flip(Fast-SSC-Flip-CS)譯碼算法的性能。SSC-O racle譯碼算法是一種理想的Fast-SSC譯碼算法，該算法能夠完美糾正Fast-SSC譯碼過程中由信道噪聲導致的單個錯誤比特，即該算法的性能代表單比特翻轉Fast-SSC算法的譯碼性能上限。

算法3 CFS-Fast-SSC-Flip譯碼算法

當設置極化碼的參數N=512,R=0.5時，上述各個譯碼算法的BER性能曲線如圖5(a)所示。從圖5(a)可以看出所提的CFS-Fast-SSC-F lip譯碼算法與N-Fast-SSC-Flip譯碼算法的BER性能曲線幾乎保持一致，相較于傳統的Fast-SSC-Flip譯碼算法以及Fast-SSC-Flip-CS譯碼算法，所提的CFSFast-SSC-F lip譯碼算法并沒有明顯的BER性能損失。相較SC,Fast-SSC譯碼算法在BER=10-3條件下有0.78 dB的性能增益。

圖5 CFS-Fast-SSC-Flip譯碼算法與各種譯碼算法在R =0.5時BER性能比較圖

類似地，圖5(b)表示N=1 024,R=0.5時上述的各個譯碼算法的BER性能數值仿真圖。綜合圖5(a)與圖5(b)可得，所提的CFS-Fast-SSC-Flip譯碼算法與N-Fast-SSC-Flip譯碼算法的BER性能曲線幾乎保持一致，相較于傳統的Fast-SSC-Flip譯碼算法以及Fast-SSC-F lip-CS譯碼算法，所提的CFSFast-SSC-Flip譯碼算法并沒有明顯的BER性能損失。

類似地，圖6(b)表示在極化碼參數N=1 024,R=0.5時上述的各個譯碼算法的FER性能數值仿真圖。通過觀察兩圖可以發現，提出的CFS-Fast-SSC-Flip算法的譯碼性能略優于傳統的Fast-SSCFlip譯碼算法以及Fast-SSC-Flip-CS譯碼算法，且與N-Fast-SSC-Flip譯碼算法的性能幾乎相同。

為了研究CFS-Fast-SSC-Flip譯碼算法的性能開銷以及譯碼延遲，本節利用翻轉譯碼算法的平均迭代次數Iave來表示每一幀需要進行譯碼的次數，其最小和最大的迭代次數分別為1和Tmax+1。Iave的計算方法為

為了更好地分析所提算法的譯碼延遲[18]，對各種算法的時鐘周期(C lock Cycles,CC)進行比較。為了便于表述每個譯碼階段所消耗的CC數，其中Fast-SSC譯碼算法消耗的CC數、排序操作消耗的CC數、CRC校驗消耗的CC數以及一輪額外迭代的CC數分別用CFast-SSC，CSort，CCRC以及CExtra進行表示。假設在第1次譯碼過程中，首先進行Fast-SSC譯碼操作，然后執行排序操作，其中CRC校驗和排序操作同時執行。因此在第1次譯碼過程中消耗的C1=CFast-SSC+CSort。在額外的迭代譯碼過程中仍然先執行Fast-SSC譯碼操作，與第1次譯碼不同的是，后續的迭代譯碼過程不需要進行排序操作。因此，每一輪額外的迭代譯碼消耗的CExtra=CFast-SSC+CCRC。綜上，譯碼一幀所需CC數量的計算表達如式(16)所示

由于所對比的幾種不同算法均基于Fast-SSC，在保持參數一致的情況下，譯碼過程中消耗的CFast-SSC，CCRC一致。因此，譯碼一幀中消耗的CC數量取決于CSort。傳統的Fast-SSC-Flip譯碼算法對K個信息比特的LLR值進行排序，而CFS-Fast-SSC-Flip僅對CFS中η個信息比特的LLR值進行排序。在排序過程中消耗的時鐘周期CSort(η)＜CSort(K)。由表2可以得到，本文所提的CFS-Fast-SSC-Flip譯碼算法的平均迭代次數Iave要小于等于目前現存的Fast-SSC-Flip譯碼算法。綜上，本文所提算法的譯碼延遲要優于Fast-SSC-Flip算法、且與N-Fast-SSC-Flip譯碼算法的譯碼延遲接近。

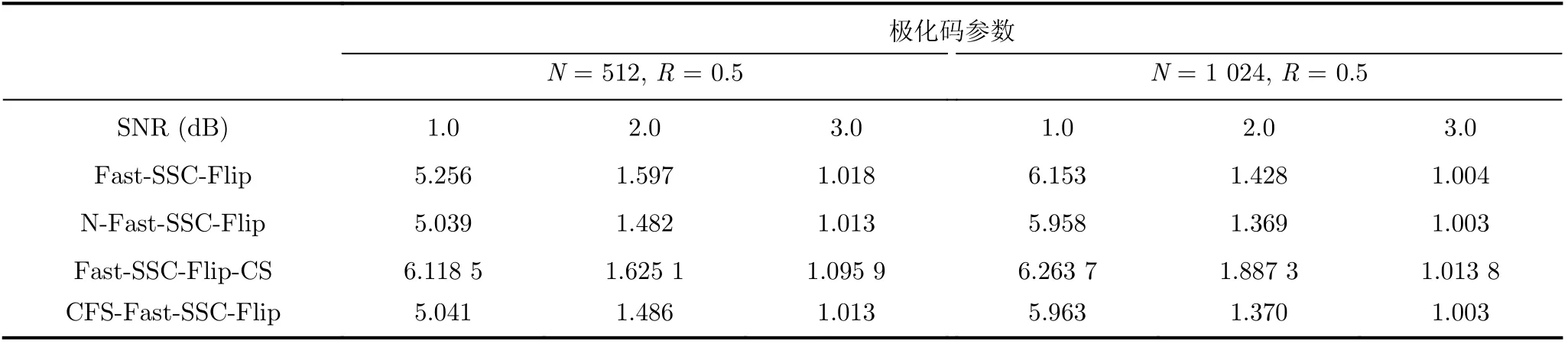
表2 各種譯碼算法的平均迭代次數

本文所提的CFS-Fast-SSC-F lip譯碼算法相較于傳統Fast-SSC-Flip以及N-Fast-SSC-Flip譯碼算法的一個直觀優勢是在候選比特的搜索效率。傳統的Fast-SSC-Flip譯碼算法在搜索候選比特方面的復雜度為O(Klog2K)，而CFS-Fast-SSC-F lip譯碼算法的搜索復雜度為O(ηlog2η)。其中K表示信息比特集合大小，η表示CFS集合的大小。

表3比較了本節所提的CFS相較于傳統的Fast-SSC-Flip所使用的候選翻轉比特集合大小。從表3可以得到本文所提的CFS集合的大小在不同極化碼編碼參數以及信噪比的情況下都要小于傳統的Fast-SSC-Flip譯碼算法所使用的候選翻轉比特集合大小。在極化碼的碼長N=1 024，碼率R=0.5，本文所提的CFS-Fast-SSC-Flip譯碼算法相較于傳統Fast-SSC-Flip(N-Fast-SSC-F lip與傳統Fast-SSC-Flip兩種譯碼算法的候選翻轉比特集合大小相同)，至少能縮小77.93%的候選翻轉比特集合大小。

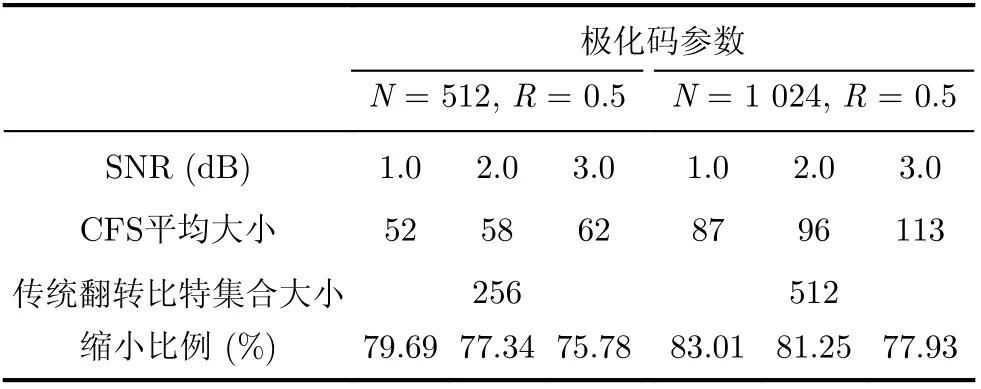
表3 CFS與傳統Fast-SSC-Flip譯碼算法的候選翻轉比特集合大小比較

6 結論

本文從縮小Fast-SSC-Flip譯碼算法中的候選翻轉比特集合大小出發來提升Fast-SSC-Flip的候選比特搜索效率，由此提出了CFS-Fast-SSCFlip。本文所提的CFS能夠有效地包含候選翻轉比特，但集合大小遠小于全部信息比特集合大小，從而減小搜索復雜度。實驗結果表明，本文提出的基于CFS的Fast-SSC-F lip算法在和N-Fast-SSCF lip取得相近的譯碼性能和平均迭代次數的情況下，顯著地縮小了候選翻轉比特集合的大小，減小了搜索復雜度，提升了候選比特的搜索效率。