金屬網在剛性彈頭靜壓下的力學性能分析

黃祺臨，汪 敏，陳輝國，周 帥

(陸軍勤務學院軍事設施系，重慶 401311)

金屬網是指由鋼絲編織成的三維網狀結構(圖1)[1]，因其具有重量輕、力學性能優異等特點，在工程領域應用愈加廣泛。在交通工程中，應用金屬網作為主要組成構件的防護裝置(如被動防護網、主動防護網等)，用于攔截落石、泥石流等自然災害[2-3]；在建筑工程中，采用金屬網對鋼筋混凝土結構構件進行加固，提高構件的承載能力和延展性等[4-6]；在防護工程中，增設金屬網加強鋼筋混凝土結構抗侵徹、抗爆炸等防護性能[7-8]，利用金屬網作為攔截颶風中風力卷起的碎片，從而降低撞擊戶外門窗而引起的破壞等[9-10]。隨著編織用鋼絲強度、韌性等的提高，利用高強鋼絲編織而成的金屬網在輕型坦克或裝甲車的格柵裝甲中也得到了應用(圖1～圖2)，主要目的是用于攔截近程武器(如火箭彈、迫擊炮彈等)的打擊，提高戰時輕型坦克或裝甲車的生存概率[11-13]。

圖1 金屬網格柵裝甲Fig.1 Wire nets grille armor

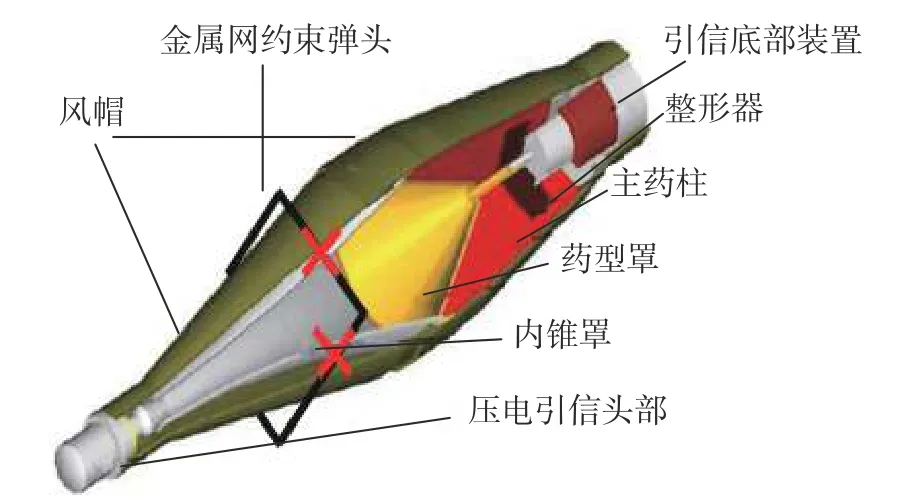
圖2 彈頭與金屬網間的相互作用Fig.2 Interaction between the warhead and the wire nets

關于高強金屬絲編織而成的金屬網，相關力學性能研究較多，但主要集中在落石災害防治領域。在靜力性能研究方面，主要考慮金屬網平面內雙向拉伸性能[14]、平面外抗頂破性能等[15-16]。然而，為提高金屬網攔截近程武器的效率，金屬網在彈頭靜壓下的力學性能研究是一個重要的工作，這對于理解金屬網與彈頭相互作用下的力學性能和破壞特點，合理設計金屬網的網孔尺寸和規格等都具有較好的指導意義。

圖3 中給出了金屬網的實彈攔截試驗及破壞情況。從圖中可以看出，金屬網在彈體打擊作用下的破壞局限于單個網孔區域，這與落石沖擊金屬網存在明顯的區別[17]。從目前的研究成果看，現階段關于金屬網的抗頂破性能試驗，主要是根據落石災害實際情況而設計的試驗裝置和試驗方法，獲得金屬網在頂破作用下的荷載-位移曲線和承載力理論計算方法[18]，為落石災害防護中的金屬網選型和設計提供參考。但根據落石災害特點而設計的金屬網試驗條件與彈頭和金屬網相互作用的狀態差別較大，對研究金屬網在彈頭靜壓下力學性能的借鑒作用有限。

圖3 金屬網的實彈攔截試驗及破壞情況Fig.3 Short-weapon intercepted tests and the fracture feature of the wire nets

基于以上原因，為研究金屬網在彈頭靜壓下的力學性能，結合金屬網的實彈攔截試驗情況和破壞特點，設計了剛性彈頭加載裝置和金屬網靜壓試驗平臺，開展了直徑為82 mm 和107 mm 的彈頭加載裝置靜壓金屬網的試驗，分析了金屬網的破壞特點。此外，在試驗研究的基礎上，建立了剛性彈頭加載裝置靜壓金屬網的理論模型，推導了剛性彈頭加載裝置靜壓金屬網臨界荷載的理論計算方法，研究成果可為金屬網攔截彈體的初步設計提供參考依據。

1 剛性彈頭靜壓金屬網的試驗設計

1.1 剛性彈頭加載裝置和金屬網的設計

由于近程武器種類繁多，形狀各異，根據典型近程武器的外形和試驗加載條件[19]，設計了口徑為D=82 mm和D=107 mm兩類剛性彈頭加載裝置，前半部分按彈頭外形制作，后半部分為彈頭支撐部分，用以保證試驗的正常進行。彈頭加載裝置的布置及具體尺寸如圖4(a)所示，制作的剛性彈頭加載裝置見圖4(b)。

圖4 剛性彈頭加載裝置尺寸及照片Fig.4 Dimensions and photos of rigid warhead loading device

根據彈體口徑，設計了金屬網的尺寸，如圖5所示。圖中：d為編網鋼絲直徑；x為沿水平方向菱形網孔短邊尺寸；y為沿豎直方向菱形網孔長邊尺寸； β為菱形網孔銳角；Di為網孔內切圓直徑；ht為沿平面外法線方向外邊界厚度；hi為內凈厚度。金屬網近似為正方形，nL≈1 m，nQ≈1 m。試驗中，共設計了2 種鋼絲直徑編織而成的金屬網，具體參數見表1(由于金屬網為松散結構，因此表中為拉緊后的尺寸)。

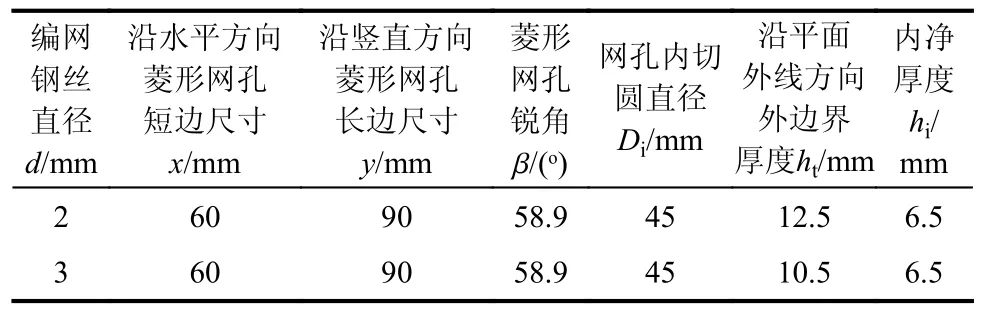
表1 金屬網規格尺寸參數Table 1 Size parameters of the wire nets

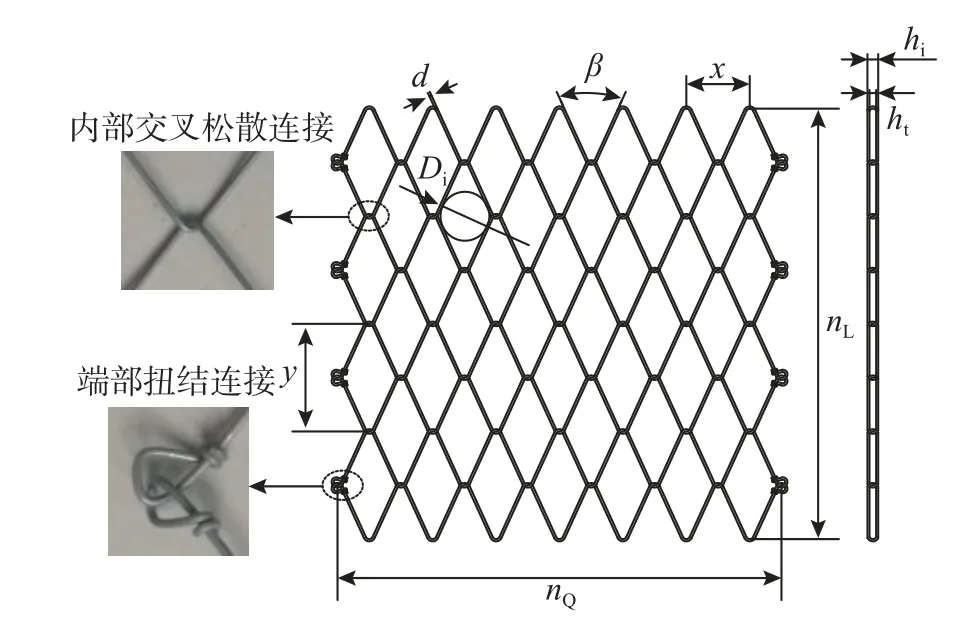
圖5 金屬網規格尺寸圖Fig.5 Specification and dimension drawing of wire nets

1.2 靜壓試驗平臺設計

設計的靜壓試驗平臺如圖6(a)所示，外輪廓尺寸為2 m×2 m×1.5 m，其中主要部件為金屬網懸掛與張拉裝置，如圖6(b)所示。

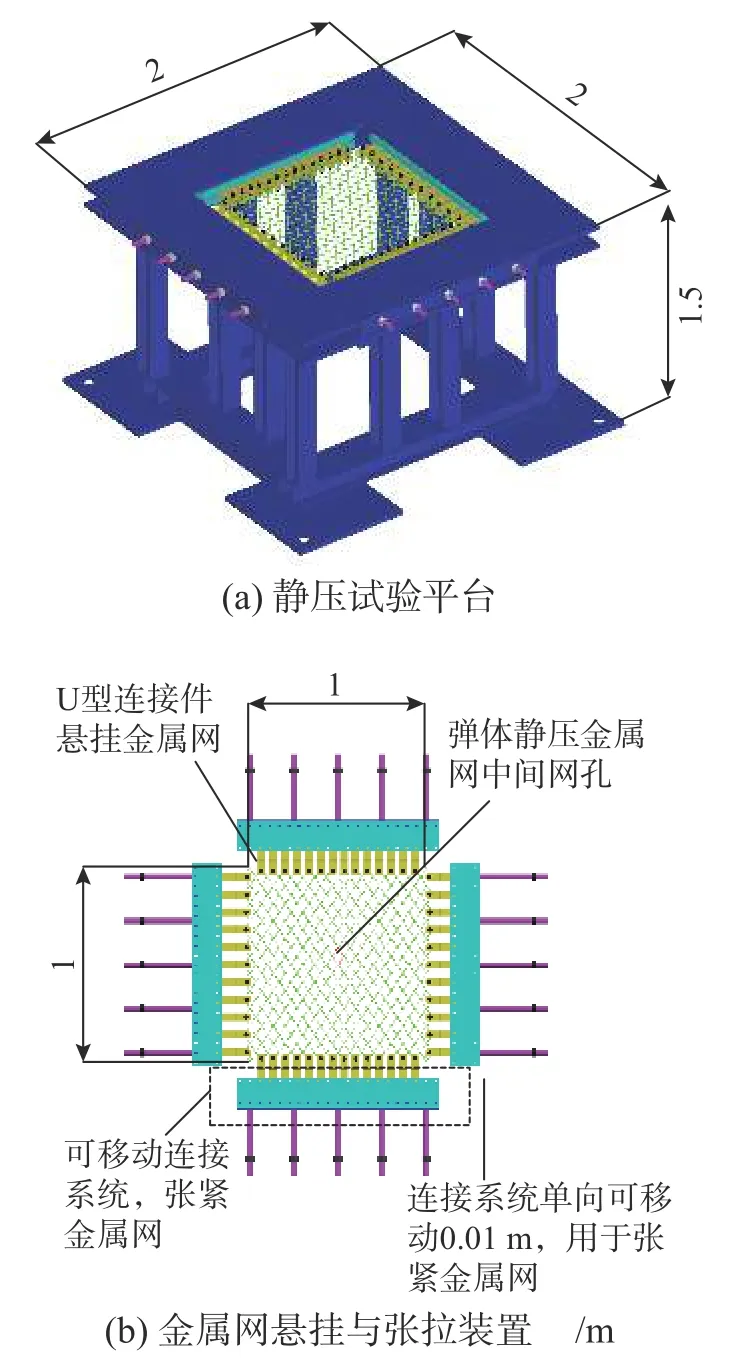
圖6 金屬網靜壓試驗平臺尺寸及細部圖Fig.6 Dimensions and details of static pressure experimental platform for the wire nets

金屬網懸掛與張拉裝置分為兩部分：一部分為連接金屬網的U 型連接件；另一部分為可移動連接系統。U 型連接件可以固定金屬網的四個邊界，約束金屬網平面內的自由度；可移動連接系統可以對金屬網進行張拉，單側單向可張拉約0.01 m，這樣可以保證每次試驗前，金屬網均處于張緊狀態。試驗平臺可開展1 m×1 m 金屬網的靜壓試驗。

1.3 試驗加載方案設計

考慮到金屬網的幾何大變形特性，靜壓試驗在20 kN 液壓試驗機上進行，液壓試驗機行程為500 mm。試驗開始前將彈頭加載裝置的連接板與試驗機端承板連接，彈頭對準金屬網中間菱形網孔的中間位置(見圖6(b)、圖7)。

圖7 剛性彈頭加載裝置安裝照片Fig.7 Installation photo of rigid warhead loading device

根據金屬網規格(表1)和加載彈頭直徑情況(圖4)，開展了2 類金屬網、2 類彈頭加載裝置共8 次破壞性試驗，具體如表2 所示。試驗時，彈頭加載裝置下壓采用位移速率控制，即彈頭以勻速慢慢往下壓，彈體的下壓速度為10 mm/min。當彈頭與金屬網接觸、彈頭受到反向荷載作用時，記錄彈體向下的位移與反向荷載，待金屬網破壞后即停止加載，讀取并繪制荷載-位移曲線。

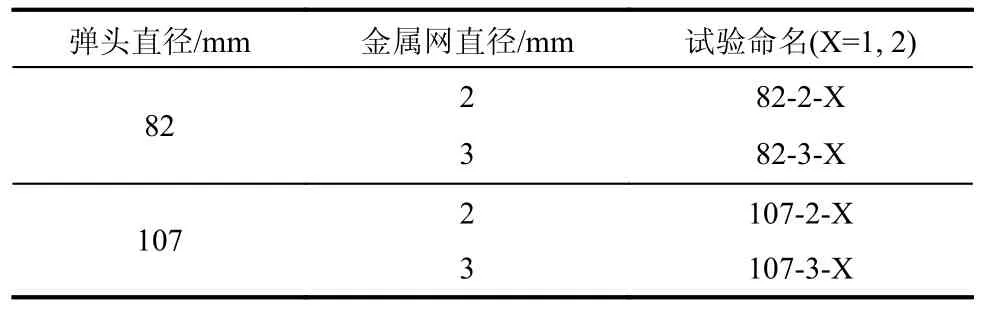
表2 靜壓試驗加載方案Table 2 Test loading scheme for static pressure

2 靜壓試驗結果分析

根據試驗情況，可以將金屬網與剛性彈頭加載裝置間的相互作用分為以下4 個狀態(圖8)。

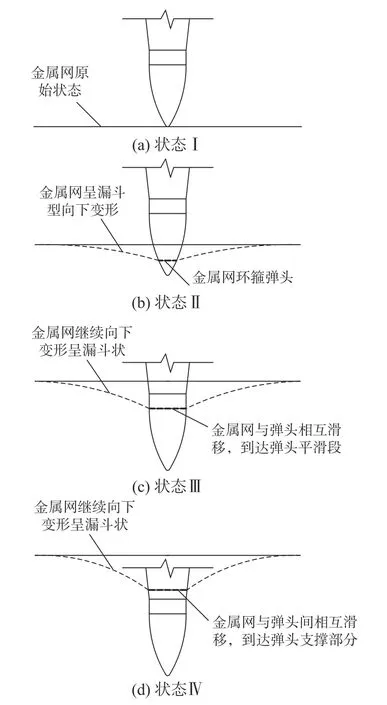
圖8 金屬網與剛性彈頭加載裝置間相互作用的狀態圖Fig.8 State diagram of interaction between the wire mesh and the rigid warhead loading device

狀態Ⅰ：彈頭加載裝置緩慢向下移動，彈頭前端與金屬網平面接觸。

狀態Ⅱ：彈頭部分居中垂直插入金屬網菱形網孔中，金屬網中菱形網孔被彈頭擠壓逐步擴大，同時逐漸變成彈頭剖面形狀并環箍住彈頭。當金屬網環箍作用力達到一定程度時，金屬網與彈頭一起向下移動，金屬網整體變形呈現漏斗型。

狀態Ⅲ：隨著金屬網中菱形網孔在彈頭環向擠壓和豎向拉伸共同作用下，菱形網孔進一步擴大，造成網孔對彈頭的環箍力無法限制金屬網與彈頭之間的相對位移，金屬網隨著彈頭繼續向下變形的過程中，與彈頭發生相對位移。

狀態Ⅳ：金屬網在隨著彈頭繼續向下變形的過程中，與彈頭也存在一定程度上的相對位移，到達彈頭加載裝置的支撐部分。

由于金屬網與彈頭加載裝置間的相互作用比較復雜，金屬網不斷受到加載裝置向下靜壓的運動過程中，分為整體變形和局部變形。整體變形為金屬網受到的漏斗型拉伸變性，局部變形為金屬網中菱形網孔受到的彈頭擠壓變形。在這個過程中，金屬網的網孔尺寸和彈頭的直徑等對靜壓過程均有影響。根據彈頭直徑的不同，金屬網所經歷的狀態也有所區別。

對于82 mm 彈頭的靜壓試驗，金屬網的變形均經過了圖8 所示的四個狀態，進入狀態Ⅳ后，與彈頭接觸部分的菱形網孔中鋼絲交接處發生斷裂，狀態Ⅱ、狀態Ⅳ的情況如圖9 所示。對于107 mm彈頭的靜壓試驗，金屬網的變形僅經歷了圖8 所示的兩個狀態，由狀態Ⅱ到狀態Ⅲ的過度過程中，與彈頭接觸部分的網孔發生破壞。

圖9 金屬網與彈頭相互作用的試驗照片Fig.9 Test photos of interaction between the wire mesh and the warhead

82 mm 彈頭和107 mm 彈頭靜壓金屬網造成的破壞形態基本一致。圖10 中給出了典型的金屬網在彈頭加載裝置靜壓下的破壞照片，從圖中可以看出，除了與彈頭加載裝置接觸部分的菱形網孔發生變形，逐步接近于彈頭剖面形狀直至破壞外，其余部分的網孔基本保持為菱形；接觸部分的菱形網孔破壞位置均位于鋼絲交叉節點處。對比圖3和圖10 可以看出，實彈打擊和剛性彈體靜壓金屬網的破壞形態基本一致，其最終破壞均僅局限于網孔與彈體接觸部位。

圖10 金屬網網孔破壞后照片Fig.10 Photos of the wire mesh after fracture

圖11～圖12 中分別給出了82 mm 彈頭和107 mm彈頭加載裝置靜壓金屬網的荷載-位移曲線圖，對比分析圖11～圖12 可以看出：

圖11 82 mm 彈頭加載裝置靜壓金屬網的荷載-位移曲線Fig.11 Load displacement curves of static pressure for the wire mesh of 82 mm rigid warhead loading device

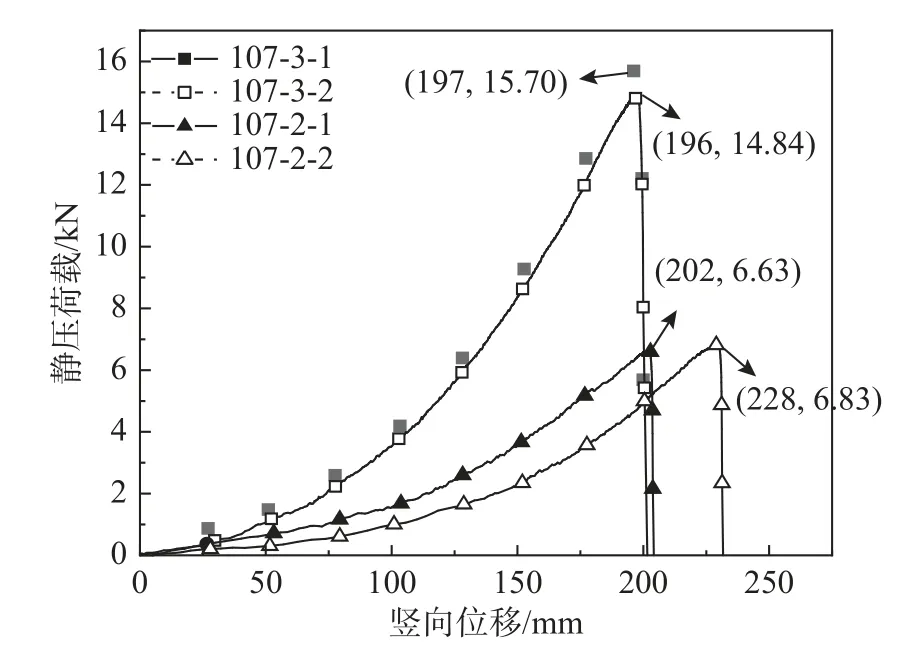
圖12 107 mm 彈頭加載裝置靜壓金屬網的荷載-位移曲線Fig.12 Load displacement curves of static pressure for the wire mesh of 107 mm rigid warhead loading device

1) 82 mm 彈頭加載裝置靜壓金屬網的荷載-位移曲線經歷上升-下降/近似平穩-上升三個階段。在第一個上升階段，彈頭存在3 個狀態，第一個狀態的峰值荷載發生時，金屬網位于彈頭加載裝置的平滑段起始部分(對應圖8 中的狀態Ⅲ)；第二個狀態，金屬網在彈頭平滑段時，由于此處彈頭直徑保持不變，豎向荷載突然降低，并保持一段距離(對應圖8 中由狀態Ⅲ轉換到狀態Ⅳ的過程)；第三個狀態，荷載隨著彈頭加載裝置的向下位移，逐步增大，直到金屬網發生破壞(對應圖8中的狀態Ⅳ)。

2) 對于107 mm 彈頭靜壓金屬網，豎向荷載隨著彈頭加載裝置的向下位移逐漸增大，直到破壞(對應圖8 中的狀態Ⅰ和狀態Ⅱ)。

3) 82 mm 彈頭靜壓作用下，隨著約束彈頭的菱形網孔逐步擴大，金屬網與彈頭間存在滑移、平衡、滑移反復過程，因此，豎向荷載隨著彈頭下壓位移的增大，增長趨勢比較平緩；而在107 mm彈頭的作用下，由于金屬網與彈頭間滑移較小，金屬網中菱形網孔在拉伸、擠壓共同作用下發生了破壞。

3 剛性彈頭靜壓金屬網的理論分析

3.1 理論分析模型及計算方法

在剛性彈頭加載裝置靜壓金屬網的試驗中，由于彈頭靜壓裝置作用在金屬網中間位置的單個菱形網孔中，菱形網孔的四個邊為對稱受力，因此可利用金屬網中菱形網孔單元的對稱性，建立理論模型進行分析進行計算。

根據圖8 所示狀態，當金屬網中菱形網孔與彈頭相互位置在圖13 中A-A 所示位置時，金屬網中單個菱形網孔中鋼絲發生斷裂(即由狀態Ⅱ過度到狀態Ⅲ的過程中)，此時，可認為彈頭A-A 剖面為金屬網臨界破壞面。

圖13 彈頭與金屬網相互作用位置示意圖Fig.13 Schematic diagram of interaction position between the warhead and the wire mesh

取與彈頭接觸部分菱形網孔的一個微段進行力學分析，假設此微段受到彈頭的作用力q沿著彈頭部分與金屬網接觸部位的切線方向，則可以把作用力q分解為兩個方向的力：一個是水平方向，為微段受到的彈頭擴張力qh(根據作用力與反作用力原理，即為菱形網孔對彈頭的環箍力)；另一個是豎直方向，為金屬網抵抗彈頭加載裝置向下運動的力qv(也即彈頭受到的豎向荷載)。因此，根據圖13所示的受力分析圖，可得彈頭受到的豎向荷載為：

式中， γ為摩擦角。

根據彈頭部分的形狀參數特征，通過幾何分析可得正切摩擦角：

式中：R0為彈頭部分的曲線半徑；x0為彈頭部分的曲線圓心O1橫坐標；R為臨界破壞面(A-A 剖面)彈頭的半徑(設計彈頭剖面為圓形)。

由于彈頭加載裝置與金屬網相互作用時，彈頭加載裝置被套箍在金屬網的單個菱形網孔內，直至菱形網孔中的鋼絲破斷，且初始為菱形的單個網孔會隨著彈頭加載裝置的逐漸下壓而與彈頭加載裝置部分充分接觸。為需考慮金屬網中的菱形網孔與彈頭加載裝置之間的相互作用，取A-A剖面進行分析(圖14)。

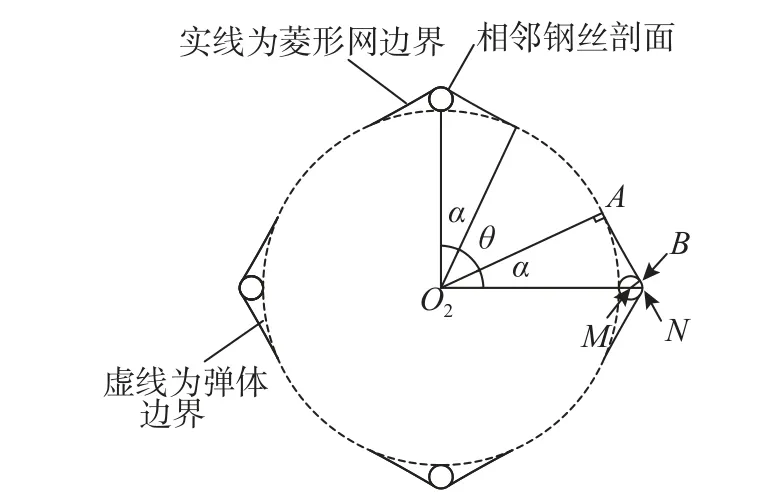
圖14 彈頭作用于菱形網孔A-A 剖面示意圖Fig.14 Schematic diagram of section A-A of warhead acting on diamond mesh

從圖14 中可以看出： ΔO2AN～ΔMBN，因此，有如下等式成立：

故有：

簡化式(4)，可得彈頭與金屬網1/4 非接觸段半角余弦為：

因此，彈頭與金屬網接觸角為：

式中，d為鋼絲直徑。

取圖14 中1/4 彈頭范圍進行分析，繪制幾何關系如圖15 所示。

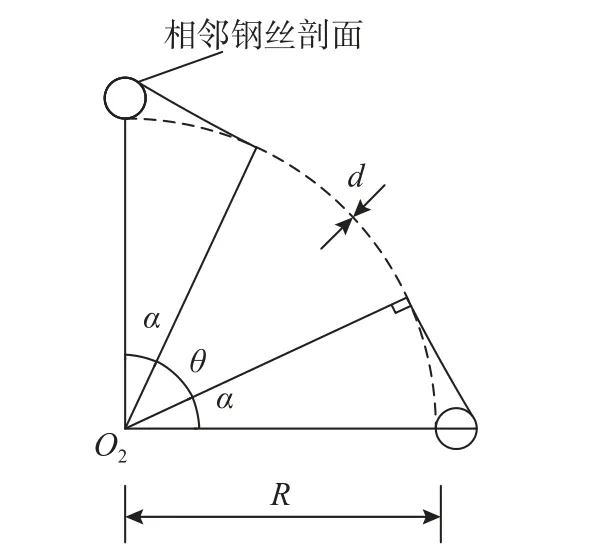
圖15 1/4 彈頭范圍內接觸幾何關系示意圖Fig.15 Schematic diagram of contact geometry within the range of 1/4 warhead

通過幾何相互關系，可得彈頭與菱形網孔接觸部分的長度為：

在忽略與臨近鋼絲接觸部分誤差情況下(即忽略與圖15 中小圓接觸部分和金屬網平面外的尺寸情況下)，1/4 彈頭范圍內鋼絲總長為：

聯立式(8)、式(9)可得：

式中：x菱形網孔短邊尺寸；y菱形網孔短邊尺寸；l為菱形網孔單邊邊長。

考慮該1/4 彈頭范圍內受力情況，彈頭與金屬網中菱形網孔接觸段受力情況如圖16 所示。

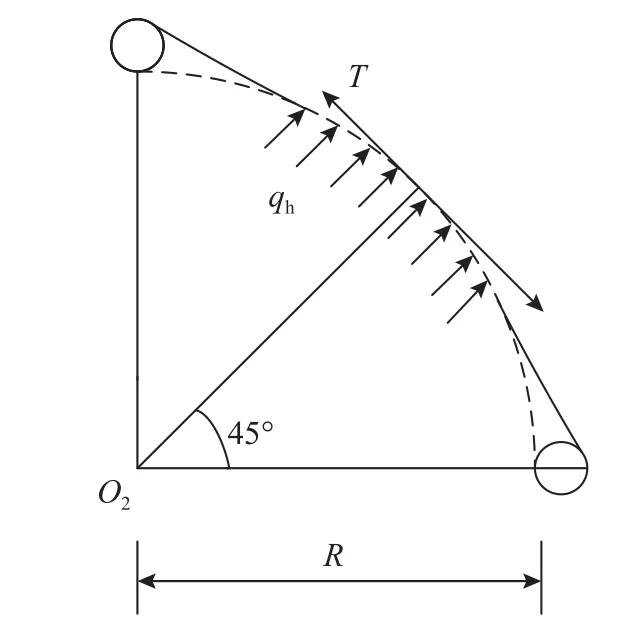
圖16 接觸段受力示意圖Fig.16 Schematic diagram of contact section stress

盡管考慮到彈頭下壓時金屬網中的菱形網孔鋼絲在交叉節點位置發生斷裂(見圖10 所示)，此時菱形網孔交接位置鋼絲會受到軸力和彎矩的耦合作用[14]，但由于金屬網的厚度很小，在鋼絲交叉位置承受的彎矩也較小，同時綜合8 次破壞試驗的結果和試驗現象可知，交叉處鋼絲的斷裂主要由軸力控制，因此可忽略彎矩對鋼絲斷裂的影響。

綜合以上假設，設鋼絲在單軸拉伸荷載下的破斷力為T，根據圖16 的計算簡圖，在45°對角線方向建立靜力平衡方程有：

求解式(11)可得鋼絲破斷力為：

又由式(1)可得豎向荷載為：

求和即可得靜壓臨界荷載：

聯立式(5)、式(6)和式(11)，并代入式(14)進行整理，得到剛性彈體靜壓金屬網的靜壓臨界荷載為：

需要說明的是，對于82 mm 彈頭加載裝置靜壓金屬網，當彈頭加載裝置的支撐部分與金屬網網孔接觸時(即進入狀態Ⅳ以后)，金屬網中單個菱形網孔中鋼絲發生了破斷，因此，相關的理論計算取彈頭加載裝置的支撐部分的幾何特征形狀進行分析，其理論推導過程與由狀態Ⅱ過度到狀態Ⅲ的基本一致。

3.2 算例分析

對2 mm、3 mm 高強鋼絲進行了單軸拉伸試驗，獲得了高強鋼絲的單軸拉伸工程應力-應變關系曲線，如圖17 所示。從圖17 中可以看出，2 mm和3 mm 高強鋼絲的單軸極限抗拉應力基本一致，均約為1860 MPa。

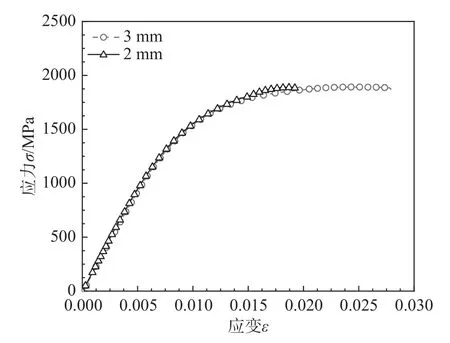
圖17 高強鋼絲單軸拉伸應力-應變關系曲線Fig.17 Uniaxial tensile stress-strain relationship curve of high-strength steel wire

結合圖4 彈頭相關尺寸和圖5 金屬網的相關參數，利用第3.1 節的理論計算方法，即可求得剛性彈頭加載裝置靜壓金屬網的靜壓臨界荷載，計算流程如圖18 所示。

圖18 計算流程Fig.18 Calculation flow chart

以107 mm 剛性彈頭加載裝置靜壓直徑為3 mm的金屬網為例進行計算。

1) 破壞臨界半徑。將圖5 中金屬網規格尺寸代入式(10)，可得臨界半徑：

2) 摩擦角。將圖13 中彈頭曲線參數代入式(2)，可得摩擦角正切值：

3) 非接觸半角。根據圖14 彈頭作用于菱形網孔A-A 剖面示意圖，代入式(5)，可得非接觸半角：

4) 接觸角。根據圖14 剖面示意圖，代入式(6)可得接觸角：

5) 鋼絲單軸拉伸極限破斷力。按圖17，3 mm高強鋼絲的單軸拉伸的極限破斷力：

6)剛性彈頭靜壓臨界荷載。綜合前面的計算結果，代入式(15)，可得靜壓臨界荷載：

按圖18 計算流程和3.2 節的算例分析，計算了82 mm 和107 mm 彈頭靜壓裝置靜壓金屬網的靜壓臨界荷載，并與試驗結果進行了對比，結果見表3。從表3 中可以看出，理論計算獲得的靜壓臨界荷載與試驗結果非常接近，誤差均在±10%以內。

表3 剛性彈頭靜壓試驗與理論計算比較結果Table 3 Comparison between static pressure tests and theoretical calculation by the rigid warhead

3.3 誤差分析

由于金屬網屬于三維網狀結構，與彈體作用的力學機理比較復雜，因此在試驗研究的基礎上，對理論分析模型進行了簡化處理。對模型簡化可能導致的誤差進行分析如下：

1) 在試驗過程中，與彈頭相互作用的菱形網孔兩側交接節點位置，鋼絲之間存在輕微的滑移，而上、下節點位置，鋼絲之間的滑移不明顯(圖19)。這主要是由于，在試驗開始前，設計的試驗平臺給金屬網施加了初始預緊力，使得金屬網處于張緊狀態，同時由于彈頭垂直作用在金屬網正中心網孔位置，能在一定程度上降低鋼絲間的滑移。因此，理論模型忽略了鋼絲在交接節點位置滑移的影響，但這會減小臨界破壞面彈頭的半徑，從而使得理論模型計算結果偏小。

2) 由于鋼絲連接節點位置存在幾何偏心，彈頭靜壓金屬網中間部位的網孔過程中，網孔四個節點位置鋼絲均受到軸力和彎矩的耦合作用(圖19)，雖然理論分析模型中忽略了彎矩的作用，會造成理論模型計算結果偏大，但因為金屬網的破壞主要由軸力控制，且初始幾何偏心很小，因此這方面的誤差會很小。

3) 在試驗過程中，與彈頭作用的菱形網孔受到兩個方面的荷載作用：一方面是彈頭對網孔的擠壓變形；另一個方面是網孔受到的周圍其他菱形網孔中鋼絲的拉伸變形。理論模型中忽略了拉伸變形的影響，會造成理論模型計算結果偏大。

總體而言，理論模型能有效地預測彈體靜壓金屬網的臨界荷載，誤差滿足工程許可范圍。

4 結論與展望

結合金屬網的實彈攔截試驗情況和破壞特點，設計了剛性彈體靜壓金屬網的試驗方案，并開展了靜壓試驗和理論分析，得到了如下結論：

(1) 金屬網在剛性彈頭靜壓作用下呈現整體變形和局部變形，整體變形呈現向下的漏斗型變形，局部變形主要集中在金屬網與彈頭接觸的菱形網孔內，呈現逐步接近于彈頭剖面形狀的變形。金屬網的破壞主要由局部變形控制，破壞位置位于菱形網孔鋼絲交叉節點處。

(2) 基于金屬網受彈頭靜壓的試驗現象及相關結果的研究，推導了剛性彈頭靜壓金屬網臨界荷載的理論計算方法，分析了理論模型產生誤差的原因。總體而言，理論模型計算結果與試驗結果非常接近，誤差均在±10%以內。

對比靜壓試驗和實彈攔截試驗，僅就金屬網的破壞形態上來看，兩者基本一致，其破壞均僅局限于網孔與彈體接觸部位，金屬網的整體變形對彈體承受的荷載影響不大。因此，理論計算方法可在一定程度上為金屬網攔截彈體的初步設計提供參考。然而，金屬網在彈體動態沖擊作用下的影響因素很多，需要考慮高強鋼絲和彈體材料在高應變率下的動態性能、彈體的沖擊能量(速度、質量)等情況，而這些影響因素還需要結合靜力理論分析成果開展深入的研究。