在不平衡負載下三相四橋臂逆變器的控制策略

魏金成，李 琴，邱曉初

（西華大學電氣與電子信息學院,四川 成都 610039）

逆變器作為一種變換器，直接將直流電壓轉換為交流電壓給交流負載提供輸入電源。隨著電力電子技術的不斷提高，設備對負載的要求越來越高，電力電子器件中的平衡負載開始被不平衡的線性負載或非線性負載取代，這就需要逆變器具有處理平衡負載和不平衡負載供電的能力[1-3]。

當三相三橋臂逆變器三相負載平衡時，輸出電壓是對稱的；當三相負載不平衡，三橋臂無法輸出對稱電壓，因為當負載不平衡時會產生零序電壓和負序電壓。對于負序電壓，可以通過閉環控制和調制波的控制來消除，但對于零序電壓，僅僅改變三橋臂的控制策略是不能解決的[4-5]。因此，本文在三相三橋臂逆變器的基礎上，增加一條橋臂（N 橋臂），其輸出端與中性點直接相連構成回路，從而控制中性點電壓，使得在不平衡負載作用下也能輸出三相對稱電壓[6-8]。

當三相負載不平衡時，三相三橋臂拓撲結構由于拓撲結構的局限性，無法消除產生的零序電壓從而導致三相輸出電壓不對稱。三相四橋臂拓撲結構可解決三橋臂不能消除零序電壓的問題，通過引入的新橋臂為中性點電壓提供可流通回路，從而保證對稱的三相輸出電壓[9-10]。四橋臂逆變器拓撲結構如圖1 所示。由于增加了第N 橋臂，開關狀態變多且矢量圖由平面變成了空間[11]。目前，空間矢量脈寬調制(SVPWM)是三橋臂逆變器的主要調制策略，它是利用最近三矢量原則確定作用矢量，并用伏秒平衡計算作用時間，再確定切換點和發波順序。但是，逆變器在平衡負載下的調制策略，不能直接應用于不平衡負載三相四橋臂的拓撲結構[12]。

圖1 三相四橋臂逆變器拓撲結構Fig.1 The topology structure of three-phase four-leg inverter

由于三相四橋臂可由三相三橋臂拓展而成，因此，本文基于這一特殊結構，將三相三橋臂的控制策略運用到四橋臂上，對新加的第N 橋臂進行單獨控制。如果負載為平衡負載，三相三橋臂可以滿足輸出平衡電壓的要求，則只有前三橋臂運行，第N 橋臂不工作。當負載不平衡時第N 橋臂投入運行，控制輸出電壓使其滿足輸出平衡電壓的條件。

SVPWM 需要進行大量的三角函數運算，調制難度較大，而載波調制是通過比較3 個參考調制波和載波來確定輸出序列，與SVPWM 策略相比，具有易于實現的優點。為了降低調制難度，本文利用SVPWM 策略計算前三橋臂占空比，利用占空比與載波的對應關系，反解出調制波表達式，再將調制波與載波進行比較，得到一致的開關管驅動信號，其中只包含簡單的邏輯比較，大大減少了計算難度，提高了作用速度[13-14]。由于逆變器第N 橋臂直接接在負載的中性點上，因此可以控制負載的中性點電壓，將中性點電壓控制為相應的零序電壓，從而達到獨立控制第N 橋臂的目的。通過分析得到N 橋臂的占空比，同樣的利用占空比與載波的關系得到第N 橋臂所需的調制波[15]。該方法既可實現在平衡負載和不平衡負載下得到三相對稱正弦電壓，又可以降低調制算法的難度，提高響應速度。該方法和三維SVPWM 方法一致，但其實現要容易得多。

1 三相四橋臂逆變器的拓撲結構

三相四橋臂逆變器拓撲結構如圖1 所示，通過控制橋臂上開關管的開通和關斷，輸出1 和0 這2 種電平狀態，由表1 可得Sx1與Sx2互補，其中，x=a、b、c。1 表示開通，0 表示關斷。

表1 開關狀態對應的輸出狀態Tab.1 The output state corresponding to the switch state

由圖1 可知，根據基爾霍夫電壓定律（KVL）可得逆變器的輸出電壓方程為：

式中uNO為逆變器的可控變量，分別對逆變器的三相負載電壓uAN、uBN、uCN進行控制。

2 三相三橋臂逆變器單載波脈寬調制策略

圖2 為前三橋臂對應的矢量圖。圖3 為A 扇區對應的開關作用順序與作用時間，假設三相輸出電壓為：

圖2 三相三橋臂逆變器空間矢量圖Fig.2 The vector diagram of three-phase three-leg inverter

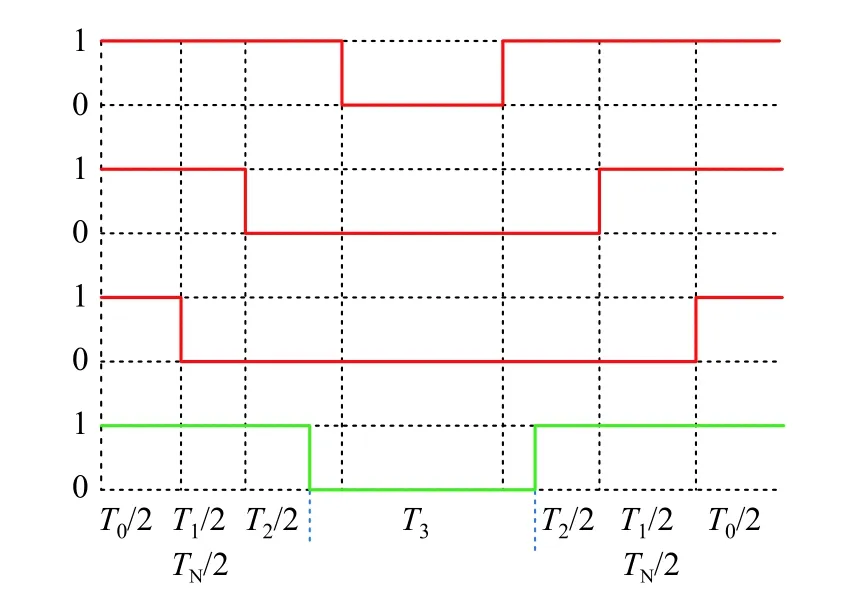
圖3 A 扇區開關狀態Fig.3 Section A sector switch status

參考電壓矢量為

根據伏秒平衡原理來計算各個矢量的作用時間，當參考矢量位于A 扇區時，伏秒平衡表達式為：

式中：V0為000；V1為100；V2為110；V3為111。解得：

若載波為-1 到0 的三角波信號，則可表示為：

由圖3 可得到各開關管在SVPWM 下的驅動信號，將此信號與載波結合可反解出對應的調制波，再將調制波與三角載波進行簡單的邏輯比較即可得到等價的開關狀態。

結合式（6）和式（7）可得：

根據SVPWM 調制的發波順序可得每個扇區所對應的開關狀態排列，如表2 所示（表中僅列出了對稱發波的一半）。由表可知，每相橋臂在6 個扇區下只有3 種排列順序。因此，最后調制波只有上述3 種表達方式，調制波公式總結如表3 所示。

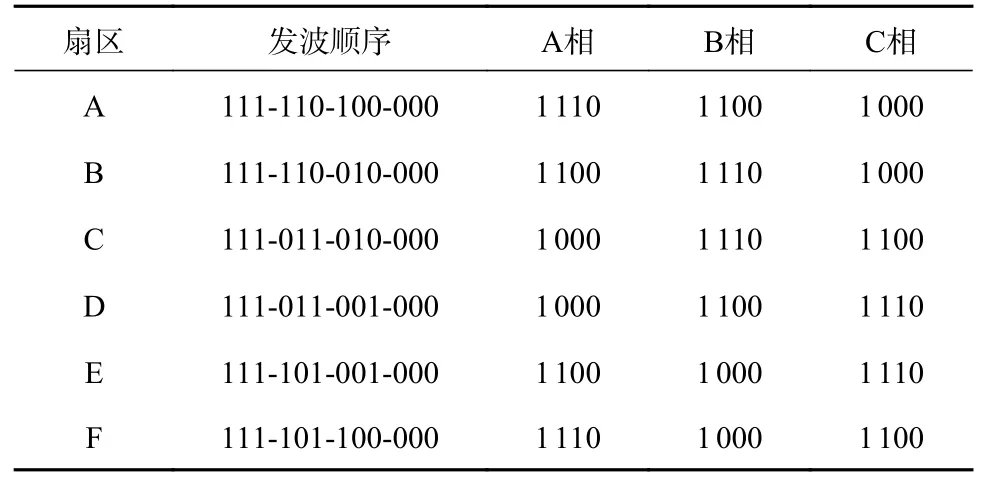
表2 扇區開關狀態排列順序Tab.2 Order of the sector switch states

表3 調制波公式總結Tab.3 Summary of the modulated wave formula

3 第N 橋臂控制策略

為了能夠輸出對稱的三相電壓，分析和推導一個周期內，產生的零序電壓。根據圖3 中逆變器的開關組合和排列順序，得到逆變器各橋臂到分電容中點（O點）的電壓，為：

代入對應的時間可得：

根據式（2）和式（10），有：

由式（11）可得urZA=urZB=urZC=urZ。同樣，可以得到其他5 個扇區的urZA、urZB、urZC，結論與式（11）相同。式（11）即為輸出電壓中除參考電壓以外的零序電壓。當負載平衡時，負載的中性點電壓等于對應的零序電壓，因此，可輸出對稱的三相正弦電壓；當負載為不平衡時，負載的中性點電壓不等于對應的零序電壓，因此，負載電壓不能輸出對稱的三相正弦電壓[15]。

由于逆變器第N 橋臂的輸出端直接與負載的中性點相連（N點），為零序電壓形成了通路，因此可以直接控制中性點電壓uNO。將式（11）代入式（1）得到：

由式（12）可知，當uNO在一個開關周期內等于零序電壓urZ就可控制輸出電壓為對稱，此時輸出電壓不受負載影響。

以逆變器A 大扇區輸出參考電壓矢量為例，逆變器作用時，對應的第N 橋臂上開關作用時間為TN，對應下開關作用時間則為TS-TN，N 橋臂輸出電壓uNO的平均值為

當uNO=urZ時，可得逆變器對應的N 橋臂上開關作用時間，為

如圖3 所示，將TN/2 代入載波式（6）有

4 仿真驗證

為了驗證單載波調制策略的可行性，在MATLAB/Simulink 中搭建仿真模型。將調制波式（8）、式（15）與載波式（6）進行簡單的比較，輸出開關管驅動信號，通過驅動信號控制開關管的開、斷，從而達到控制三相四橋臂逆變器的作用。具體實驗參數如表4 所示。

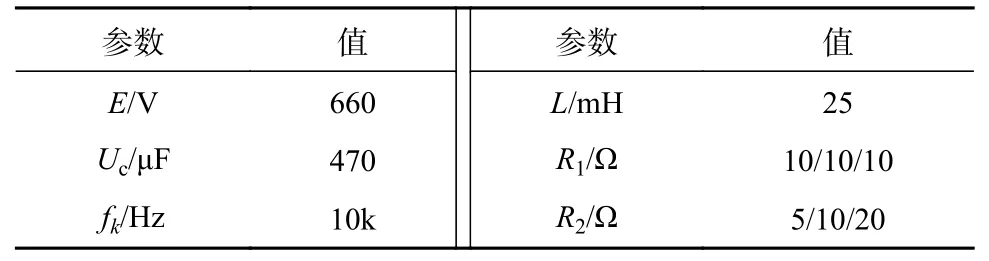
表4 仿真參數Tab.4 Simulation parameters

對比圖4、圖5：由上波形可知，逆變器在平衡負載和不平衡負載下均輸出對稱的電壓波形；由中間波形可知，當三相負載平衡時，輸出電流波形對稱，當三相負載不平衡時，逆變器的三相輸出電流不對稱，符合歐姆定律。

圖4 平衡負載R1 輸出結果Fig.4 Output result of the balanced load R1

圖5 不平衡負載R2 輸出結果Fig.5 Output result of the unbalanced load R2

上述結果表明，采用該單載波調制策略可以在負載平衡和不平衡時，利用N 相橋臂有效控制三相輸出電壓，使其都能輸出對稱的三相正弦電壓，獲得良好的輸出性能。

5 結論

三相四橋臂逆變器因引入第N 橋臂，可以有效控制輸出電壓，使得負載平衡或不平衡都可以輸出對稱正弦電壓。四橋臂SVPWM 在三維空間內調制難度大，本文采用單載波調制策略降低了四橋臂調制復雜度：前三橋臂視為普通三相三橋臂逆變器進行調制，第N 橋臂單獨調制，最終得到的調制波簡潔而有規律，不需要進行大量三角函數計算，大大降低調制難度。