基于最近發展區理論的高中數學建模習題編制與實踐*

廣東省中山市中山紀念中學(528454)梁世鋒

“課程標準”將數學建模列為數學學科核心素養之一,是新教材數學課程的核心內容,有明確的教學課時要求和任務.新教材從內容設置、屬性規模、數學抽象、有層次地設置各類數學建模素材資源及深厚的數學育人價值等信息資源.根據新教材中對數學建模問題進行劃分如下:

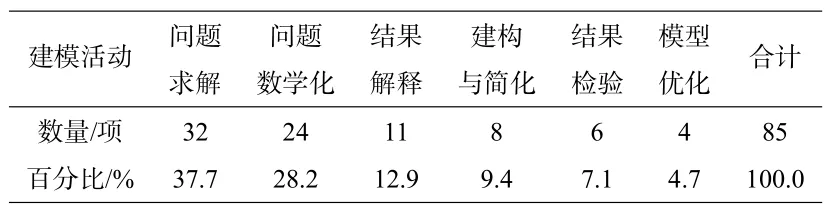
建模活動 問題求解問題數學化結果解釋建構與簡化結果檢驗模型優化合計數量/項32241186485百分比/% 37.728.212.99.47.14.7100.0

如表所示,新教材中的35 個任務共考察了85 次建模活動,其中問題求解是新教材中考察最多的活動,占總活動量的37.7%,數學化次之,占28.2%,總的來說,新教材中所涉及的建模活動覆蓋較全面,注重模型的應用能力.但在教學實踐中受限于教學課時、課堂實效、建模素材選取的便利性、考題導向以及數學建模教學定位與價值認識模糊等因素,在教學實踐中存在不少現實困境.如何編制有利于建模教學的習題或試題是值得探究的問題.

1 關于維果茨基“最近發展區”的理論概述

維果茨基“最近發展區”理論的基本觀點是學生發展有兩種水平: 一是已經達到的發展水平,表現為學生具備獨立解決問題的智力水平;二是他可能達到的發展水平.

在這種水平下學生需要借助導師引導、幫助,才能解決問題.這兩種發展水平之間的距離定義為最近發展區.我們可以用圖1 來形象地說明這個隱喻性的概念.坐標軸的方向表示思維水平的層次,當問題的思維水平要求在C以遠,則即使有幫助,該生也不能解決這問題.從坐標軸上形象地看,教學過程就是最近發展區AB的移動過程.正是由于這樣的移動,使得原本處于最近發展區里的問題,被置于現有發展水平(區)里.本文試圖從最近發展區的理念作為切入點,結合國家標準數學建模素養的三個發展水平,選取新教材的數學問題或經典習例題開展數學模型習題編制.以案例分析為背景,按照以下框架(圖2)進行數學建模問題的編制.

圖1

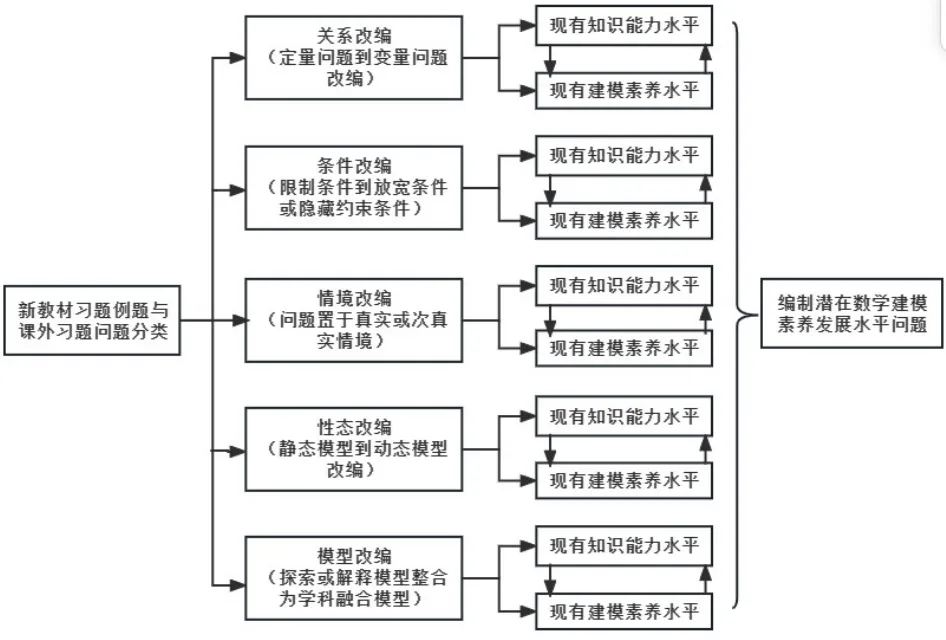
圖2

2 同源改編,從教材及試題中取材

一般來說,直接構建源于現實生活的數學建模問題有難度.實踐結果表明,立足于學生的最近發展區水平,選取課本習題適當內容為載體改編成數學建模習題或試題,有利于深化學生對內容的理解,減輕教師的工作量,是提高數學建模教學效果的一種較高效策略,筆者認為可從下面的視角改編.

2.1.關系改編,將定量關系改編為變量關系

題源: 人教版新教材必修1若用模型y=ax2來描述汽車緊急剎車后滑行的距離v與剎車時的速度x的關系,而某種型號的汽車在速度為60 km/h 時,緊急剎車后滑行的距離為20 m,在限速為100 km/h 的高速公路上,一輛這種型號的車緊急剎車后滑行的距離為50 m,問這輛車是否超速行駛?

數學建模問題當前交通繁忙,馬路上車水馬龍,怎么保持在公路上安全剎車已經成為越來越重要的問題,那么應該怎樣規范才能使人們在安全的條件下駕駛汽車,請同學們自由選擇品牌車型,研究汽車的剎車距離模型,并進一步為使用該車型里的車主提供安全的駕駛建議.

對各種影響因素進一步分析,初步建立較為完整的數學模型.

假設一.道路狀況、天氣、車輛正常行駛、車輪與路面摩擦系數等外界條件一致;

假設二.駕駛員反應時間t1為常數,車輛在反應階段作勻速直線運動,速度為v;

假設三.車輛在制動剎車做勻減速直線運動,加速度只與車型相關(即加速度為常數,制動所做的功全部用于車輛動能消耗);

假設四.剎車距離d=反應車輛行駛距離d1+車輛制動距離d2;

假設五.制動距離d2: 由制動器作用力F、車的質量m、車速v(制動時的初速度)、道路狀況、天氣狀況相關;

假設六.剎車時間用最大動力F,F作的功等于汽車動能的改變,且F與車的質量m成正比.

用現實數據來檢驗這個公式: 根據查閱資料,摩擦系數u與多種因素有關,一般為0.8 左右,雨天可降至0.2 以下,冰面就更低了,假設u=0.8,車速與剎車距離表(表3)如下:

表3

可以得出該車型車速在20km/h～100 km/h, 剎車距離與車速正相關,當然也與制動效果、天氣、地面、摩擦系數等有相關關系,可進一步研究,描出車速與剎車距離的散點圖,擬合回歸方程,估算出相應的剎車時長.

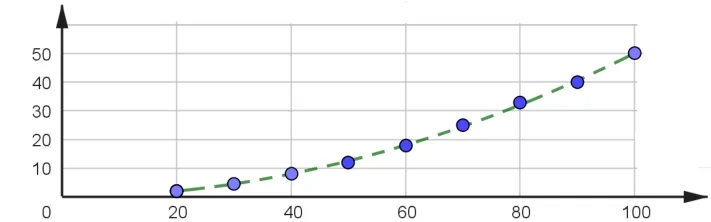
車速與剎車距離散點圖

2.2.條件改編,放寬約束條件或隱去限制條件

教材中不少習例題或已有試題中的應用題是給定條件和確定數據的,通過調整數據,減少或增加條件,放寬約束條件,隱去限制條件可以編制成數學建模問題.

題源: 模擬考題某單位有10000 名職工, 想通過驗血方式篩查乙肝病毒攜帶者, 假設攜帶病毒的人占5%, 如果對每個人逐一化驗, 就需要化驗10000 次, 統計專家提出了一種化驗方法; 隨機地按5 人一組分組, 然后將各組5人的血液混合再化驗, 如果混合血液呈陰性, 說明這5 個人全部陰性; 如果血樣呈陽性, 說明至少有一人的血樣呈陽性, 就需要對每個人再分別化驗一次, 按照這種化驗方法, 平均每人需要化驗____次.(結果保留四位有效數字)(0.955≈0.7738,0.956≈0.735,0.957≈0.6983)

混管采樣檢測是學生有生活真實體驗感受的,下面構建篩查樣本的真實情境,作以下假設:

假設一.采樣總樣本為n份,采用k份血液樣本混管檢驗;

假設二.每次檢測的時間和成本相同,人人與之間相互獨立,不傳染;

假設三.方案一,逐個檢驗;方案二,平均分成兩組,再將每組樣本混合檢驗;方案三,四個樣本混在一起檢驗.

假設四.以檢測次數的期望衡量方案的優略.

數學建模問題新冠病毒是一種通過飛沫和接觸傳播的變異病毒,篩查該病毒的一種方式是檢驗血液樣本中相關指標是否為陽性,對于n份血液樣本,有以下兩種檢驗方法: 一是逐份檢驗,則需檢驗n次.二是混合檢驗,將其中k份血液樣本分別取樣混合在一起,若檢驗結果為陰性,那么這k份血液全為陰性,從而檢驗一次就夠了;如果檢驗結果為陽性,為了明確這k份血液中究竟哪些為陽性,就需要對它們再逐份檢驗,此時n份血液檢驗的次數總共為k+1 次.某定點醫院現取得4 份血液樣本,考慮以下三種檢驗方案: 方案一,逐個檢驗;方案二,平均分成兩組,再將每組樣本混合檢驗;方案三,四個樣本混在一起檢驗.假設在接受檢驗的血液樣本中,每份樣本檢驗結果是陽性還是陰性都是相互獨立的,且每份樣本是陰性的概率為p.

(1)求兩份血液樣本混合檢驗結果為陽性的概率;

(2)若檢驗次數的期望值越小,則方案越優.那么三種方案中哪個最優? 請說明理由.(以下略,請有興趣讀者自行完成)

進一步研究,若取得為4k(k∈N?)份血液樣本,情況如何?

2.3.情境改編,將數學探究問題置于真實情境

注重構建符合學生認知的真實情境或次真實的情境,有利于激發學生學習的興趣,常見的真實情境包括生活情境、文化情境、科學情境、社會情境,將抽象的數學背景置于真實情境,有利于學生建模素養的發展.

題源: 2019 年高考全國Ⅰ卷第4 題古希臘時期, 人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是(,稱為黃金分割比例), 著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26cm,則其身高可能是( )

A.165cm B.175cm C.185cm D.190cm

數學建模問題維納斯身高與黃金分割的關系,是數學在生活場景中的應用.問題遷移,在現實生活中,不少女孩子穿著高跟鞋時,顯得腿修長美觀,那如何選配鞋跟高度才是合理的呢? 你能給出一個合理的建議方案么? 其實,這是一個具有探究現實真實情景的數學建模問題,具備現實研究價值.

假設一: 定義“美”的模型: 古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是(,稱為黃金分割比例)即采用黃金分割比例作為標準.

假設二: 女孩身高為lcm,肚臍至足底的長度dcm,鞋跟高度為xcm;

假設三: 正常比例范圍的人群范圍中采集數據,也可模擬真實正常數據.

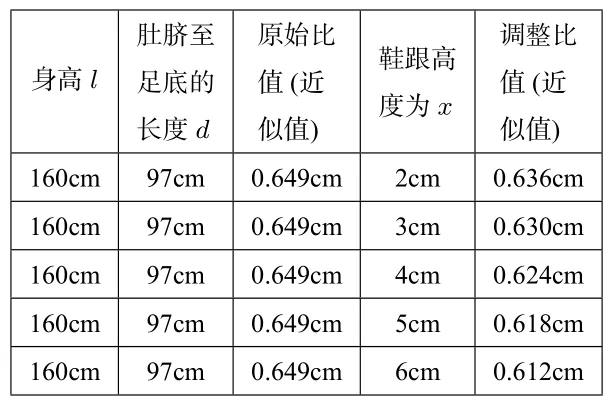
身高l肚臍至足底的長度d原始比值(近似值)鞋跟高度為x調整比值(近似值)160cm 97cm 0.649cm 2cm 0.636cm 160cm 97cm 0.649cm 3cm 0.630cm 160cm 97cm 0.649cm 4cm 0.624cm 160cm 97cm 0.649cm 5cm 0.618cm 160cm 97cm 0.649cm 6cm 0.612cm

注高跟鞋的鞋跟高度可作以下分類: 1.低高跟鞋一般是4 厘米以下;2.中跟高跟鞋一般是5-10 厘米;3.超高跟鞋一般高度為11 厘米以上;4.日常最低的高跟鞋一般是4 厘米以下,通常是5-10 厘米居多.

從數學的理性視角是選擇5 cm 鞋跟,當然根據個人舒適度選擇4 或6 厘米的鞋跟接近黃金分割比例,也是不錯的選擇.此類模型,貼近生活,有現實意義、數學工具和模型符合學生認知.

2.4.性態改編,將靜態模型轉為動態模型

新教材中的習例題或課外習題的應用探究題大多屬于靜態模型,通過將模型中的質點轉化為動態質點,對模型進行數學建模假設,構建出更符合真實情境的動態模型.考慮到運算的便利性,有時可以改編為次真實情境的動態模型.

題源: 人教版選擇性必修1 例題改編在某海濱城市附近海面有一臺風,據監測,以臺風中心為中心,半徑為20 km的圓形區域內將受到臺風影響.已知城市位于臺風中心正西40 km 處,該城市的港口位于城市中心正北30 km 處,如果臺風沿北偏西45?的直線行進,那么港口是否會有受到臺風影響?

構建臺風影響城市的次真實情境,作以下假設:

假設一.臺風沿向西偏北β方向勻速直線運動;

假設二.臺風的影響面積是圓形面積,初始半徑為r0km且半徑是勻速v2km/h 變大;

假設三.臺風中心位于城市O(如圖4)的東偏南θ方向d0km.

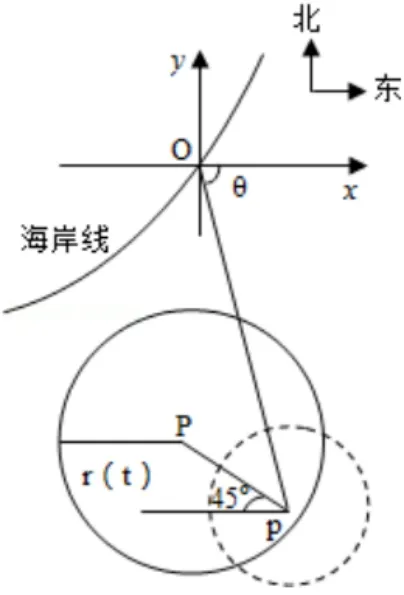
圖4

數學建模問題在某海濱城市附近海面有一臺風, 據監測, 當前臺風中心位于城市O的東偏南θ方向d0km 的海面P處,并以v1km/h 的速度向西偏北β方向移動.臺風侵襲的范圍為圓形區域, 當前半徑為r0km,并以v2km/h 的速度不斷增大.問幾小時后該城市開始受到臺風的侵襲?

若建立坐標系以O為原點,正東方向為x軸正向.此時,臺風中心(P(ˉx,ˉy))的坐標為臺風侵襲的區域是(x-)2+ (y-) ≤[r(t)]2, 其中r(t) =v2t+r0, 若在t時刻城市O受到臺風的侵襲, 則有(0-)2+(0-)2≤(v2t+r0)2.不妨賦值如下:,r0=60 km,d0=300 km,v1=20 km/h,β=45?.下面計算該城市開始受到臺風的侵襲的時刻.

解如圖4 建立坐標系以O為原點,正東方向為x軸正向.臺風中心(P(,))的坐標為

此時臺風侵襲的區域是(x-)2+(y-) ≤[r(t)]2, 其中r(t) = 10t+60,若在t時刻城市O受到臺風的侵襲,則有(0-)2+(0-)2≤(10t+60)2.即

即t2-36t+288 ≤0,解得12 ≤t≤24.即12 小時后臺風將侵襲該城市.

進一步可以研究, 若臺風是沿勻加速(特殊)曲線運動,臺風半徑膨脹是勻加速狀態的數學模型.

2.5.模型改編,探索模型與解釋模型改編為學科融合模型

題源: 課外習題已知室內溫度T1和室外溫度T2恒定不變,熱傳導過程已處于穩定狀態,即沿熱傳導方向,單位時間通過單位面積的熱量是常數.單位時間由溫度高的一側向溫度低的一側通過單位面積的熱量Q與T成正比,與d成反比,即,其中k為熱傳導系數,現有某家庭的窗戶計劃從兩種材質相同,厚度分別為d1,d2(d1

數學建模問題在現代居家裝修中,不少家庭的窗戶采用雙層玻璃,即窗戶上裝兩層玻璃且中間保留一定空隙,據說這種玻璃窗能夠減少冬天室內向室外流失的熱量或夏天減少室外流向室內的熱量.建立數學模型,試用所學的知識解釋其合理性.

模型假設

假設一.雙層玻璃和單層玻璃的室內外氣流流速及流向一致,室內室外溫差為?T;

假設二.窗戶的密封性能很好,兩層玻璃的空隙中的空氣保持靜態,即熱量的傳播無對流的單向傳導;

假設三.玻璃材料均勻,雙層玻璃每層厚度為d,雙層玻璃之間空隙寬度為l,單層玻璃厚度為2d;

假設四.用物理學熱傳導定理解釋數學模型;

假設五.室內溫度T1和室外溫度T2恒定不變,熱傳導過程已處于穩定狀態,即沿熱傳導方向,單位時間通過單位面積的熱量是常數.單位時間由溫度高的一側向溫度低的一側通過單位面積的熱量Q與T成正比, 與d成反比, 即,其中k為熱傳導系數.

根據物理定律的數學建模問題

雙層窗內層玻璃的外側溫度為Tm外層玻璃的內側溫度為Tn, 玻璃的熱傳導系數為k1, 空氣的傳導系數為k2, 單位時間單位面積的熱量傳導(即熱量流失)為, 求解得, 其中, 而厚度為2d的單層玻璃窗, 其熱傳導為,兩者之比為.

從而可以得出結論: 材質一致,雙層玻璃比單層玻璃能夠減少熱量的流失(流入).進一步探究,雙層玻璃之間的空氣層的寬度并非越大越好? 雙層玻璃單片厚度與中間空隙的合理比值是多少?

3.基于教材習例題和試題編制數學建模習題的啟示

3.1 重視教材和習題的數學建模資源整合,引導學生領悟數學建模的本質

數學建模是對現實問題的數學抽象,一般步驟為信息表述、問題求解、模型解釋、結果驗證幾個階段,通過系統挖掘并深度解析教科書中數學建模問題資源,提升學生實踐能力與創新意識,數學學習興趣的培養,體驗數學建模過程和“實踐一理論一實踐”這一循環,有助于學生數學建模素養的發展.

3.2 重視教材中建模內容的組織與改編,有助于突破建模教學的制約因素

挖掘教科書中數學問題的數學建模本質,將生活現象與社會熱點問題編制為高中數學建模習題符合學生認知最近發展區,有利于學生深化理解已有的數學問題,促進潛在建模能力水平的發展,有利于改善數學建模教學中受教學課時限制、試題命制限制、演算工具限制、教師意識限制等制約數學建模教學發展的干擾因素.因此教師應對教材素材其進行系統挖掘,并統籌編制數學建模問題,幫助學生較全面系統地理解數學建模的教育價值、科學價值及應用價值.

3.3 提升教師的數學建模素養與挖掘教材的能力,有助于學生建模素養發展

數學建模教學要求教師有較高的數學建模素養,也要求教師要準確把控教材對建模內容的數量與功能定位.基于新教材中的素材改編為學生感興趣的、符合高中課程標準的、符合學生發展水平的、體現數學建模特點的、融合技術工具、體現完整的數學建模過程的數學建模問題是有意義的.總之,在編制數學建模問題時還應關注問題情境的真實性(次真實性)、條件的約束性、問題的有效性、過程的嚴謹性、表述的閱讀性、科學工具參與性.