基于數據驅動和神經網絡的船舶機械軸承故障預測

姚 遠

(武昌工學院，湖北 武漢 430000)

0 引 言

軸承是安裝在船舶上的承受載荷和轉動力的機械裝置。軸承具有承載能力強、摩擦系數低、耐磨性好等特點，能夠保證船舶在航行過程中的穩定性和安全性。軸承的選用要考慮到船舶的使用環境和工作條件，如船舶的航行速度、載荷大小、工作溫度等因素。此外，軸承的維護保養也非常重要，定期檢查和更換軸承，保證其正常運轉，延長其使用壽命。

船舶機械軸承的故障監測技術是近年來的研究熱點，目前常用的船舶軸承故障監測手段包括振動監測、溫度監測、聲音監測和油液監測。

振動監測：通過安裝振動傳感器在軸承上監測振動信號，通過分析振動頻譜和振動特征參數，可以判斷軸承的工作狀態和故障類型。

溫度監測：通過安裝溫度傳感器在軸承上監測軸承溫度變化，當溫度異常時可以判斷軸承是否存在故障。

聲音監測：通過安裝聲音傳感器在軸承上監測軸承工作時的聲音信號，通過分析聲音頻譜和聲音特征參數，可以判斷軸承的工作狀態和故障類型。

油液監測：通過監測軸承潤滑油的溫度、壓力、粘度等參數，可以判斷軸承的潤滑狀態和故障情況。

本文針對船舶機械軸承故障監測技術，提出基于小波變換和變分模態分解(VMD)的信號處理方法，結合小波神經網絡實現了船舶機械軸承故障的信號處理和預測。

1 船舶機械軸承特性及故障分析

為了對船舶軸承故障信號進行數學建模，針對船舶機械設備最常用的滾動軸承進行建模分析。

滾動軸承是固定轉軸和其他零部件相對位置的部件，通常由內圈、外圈、滾珠和保持架組成，如圖1所示。

圖1 滾動軸承的結構示意圖Fig.1 Structure diagram of rolling bearing

船舶滾動軸承常見的失效形式包括[1]：

1）疲勞失效

長期受到往復載荷作用，導致滾道和滾珠或滾子表面出現疲勞裂紋，最終導致斷裂。

2）磨損失效

由于滾道和滾珠或滾子之間的摩擦和磨損，導致滾道表面磨損、凹坑和滾珠或滾子表面磨損、變形。

3）過載失效

當滾動軸承承受超過其額定負荷的載荷時，會導致滾珠或滾子和滾道之間的接觸壓力過大，從而引起滾珠或滾子和滾道的塑性變形或斷裂。

4）溫度過高失效

由于滾動軸承在工作過程中摩擦產生熱量，如果無法及時散熱，會導致溫度升高，從而引起潤滑劑失效、材料膨脹、變形等問題。

軸承發生故障的位置以內圈、外圈和滾動體為主。

1）滾動軸承的內圈故障

當軸承內圈發生故障時，不正常的轉動會導致振動沖擊，產生徑向載荷，內圈故障的特征頻率計算式為：

式中：Z為滾動體的個數，r為滾動軸承轉速，d為滾動體的直徑，D為滾動軸承的節圓直徑， α為滾動體接觸角。

軸承故障頻率往往為高頻，通過濾波器進行低頻濾波，可以得到軸承故障頻譜，如圖2 所示。

圖2 軸承故障高通濾波和故障頻譜Fig.2 Bearing faults, high-pass filtering and fault spectrum

2）滾動體故障

滾動體故障是船舶軸承最為常見的一種故障，伴隨著軸承過溫、異響、振動沖擊等，滾動體故障的特征頻率計算式為：

3）外圈故障

由于滾動軸承外圈固定在軸承座上，因此，當外圈出現故障時，發生沖擊載荷的位置是固定的，信號特征頻率為：

2 基于數據驅動和神經網絡的機械軸承故障預測

2.1 變分模態分解算法VMD 的信號分析技術

變分模態分解(VMD) 是一種頻域的信號分析方法，與濾波算法和傅里葉變換等相結合，能夠實現信號的準確解析。VMD 是基于變分貝葉斯方法[2]，它被用于將復雜的非平穩信號分解成一系列模態函數，通過最小化信號與模態函數之間的差異來實現信號分解。VMD 首先將信號分解成多個頻帶，每個頻帶包含一組頻率和幅度。然后，通過迭代優化的方式，確定每個頻帶的中心頻率和帶寬，以及每個頻帶中的模態函數。最后，將所有的模態函數求和，得到原始信號的近似重構。

VMD 的優點在于能夠處理非平穩信號，適用于各種信號分析和處理任務。它可以用于信號去噪、頻譜分析、模態分解等應用領域。VMD 還具有較好的自適應性，可以根據信號的特性自動選擇合適的參數。

對信號f(t)的變分模態分解過程如下：

1）假設信號有k個固有模態函數uk(t)的解。

2）建立固有模態函數uk(t)的希爾伯特變換，即

3）對信號進行頻譜調制，公式如下：

4）對調制的信號進行高斯變換：

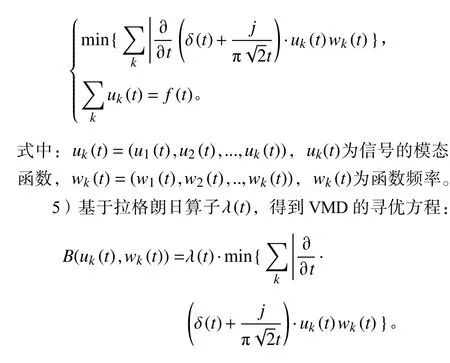
圖3 為基于VMD 算法的函數迭代示意圖。

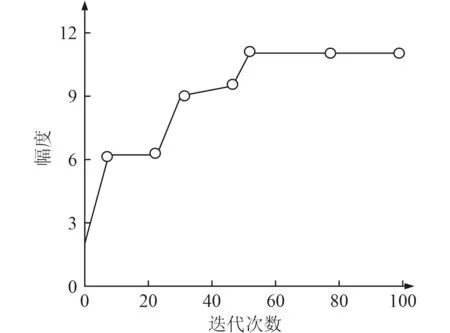
圖3 基于VMD 算法的函數迭代示意圖Fig.3 Function iteration diagram based on VMD algorithm

可知，基于VMD 模態分解在60 次的迭代次數附近，幅值不再發生變化，達到函數收斂，可見VMD模態分解算法的求解效率相對較高。

2.2 多分辨小波變換理論

多分辨小波變換分析基于小波函數的多尺度分析能力，可以將信號分解成不同尺度的頻帶[3]，并在不同尺度上對信號進行分析。在信號分解步驟中，信號經過一系列低通和高通濾波器的處理，得到不同尺度的頻帶系數。低通濾波器用于提取低頻信息，高通濾波器用于提取高頻信息。在重構步驟中，通過逆濾波器和逆小波變換，將頻帶系數重構為原始信號。

對于某非線性信號x(t)，定義其具有平方可積性，滿足：

式中：x(w)為小波函數，ω為頻率。

信號x(t)的平移與伸縮變換如下式：

式中：s為伸縮變換因子， α為平移變換因子。

信號的傅里葉變換為f(t)，則小波變換為：

常見的小波函數有：

1）Harr 小波函數

Harr 小波函數的性質包括平移不變性、尺度不變性和正交性，這些性質使得Harr 小波函數在信號壓縮、圖像處理和數據壓縮等領域有著廣泛的應用。表達式如下：

2）Morlet 小波函數

Morlet 小波函數的形狀類似于一個復指數函數，同時具有高斯包絡。它的實部表示信號的振幅變化，虛部表示信號的相位變化。通過對信號進行Morlet 小波變換，可以得到信號在不同頻率上的振幅和相位信息，從而實現信號的時頻分析。模型如下：

2.3 基于神經網絡和VMD 的軸承故障預測技術

本文結合模糊神經網絡算法和VMD 算法，建立一種船舶軸承故障預測系統，該系統的原理如圖4 所示。

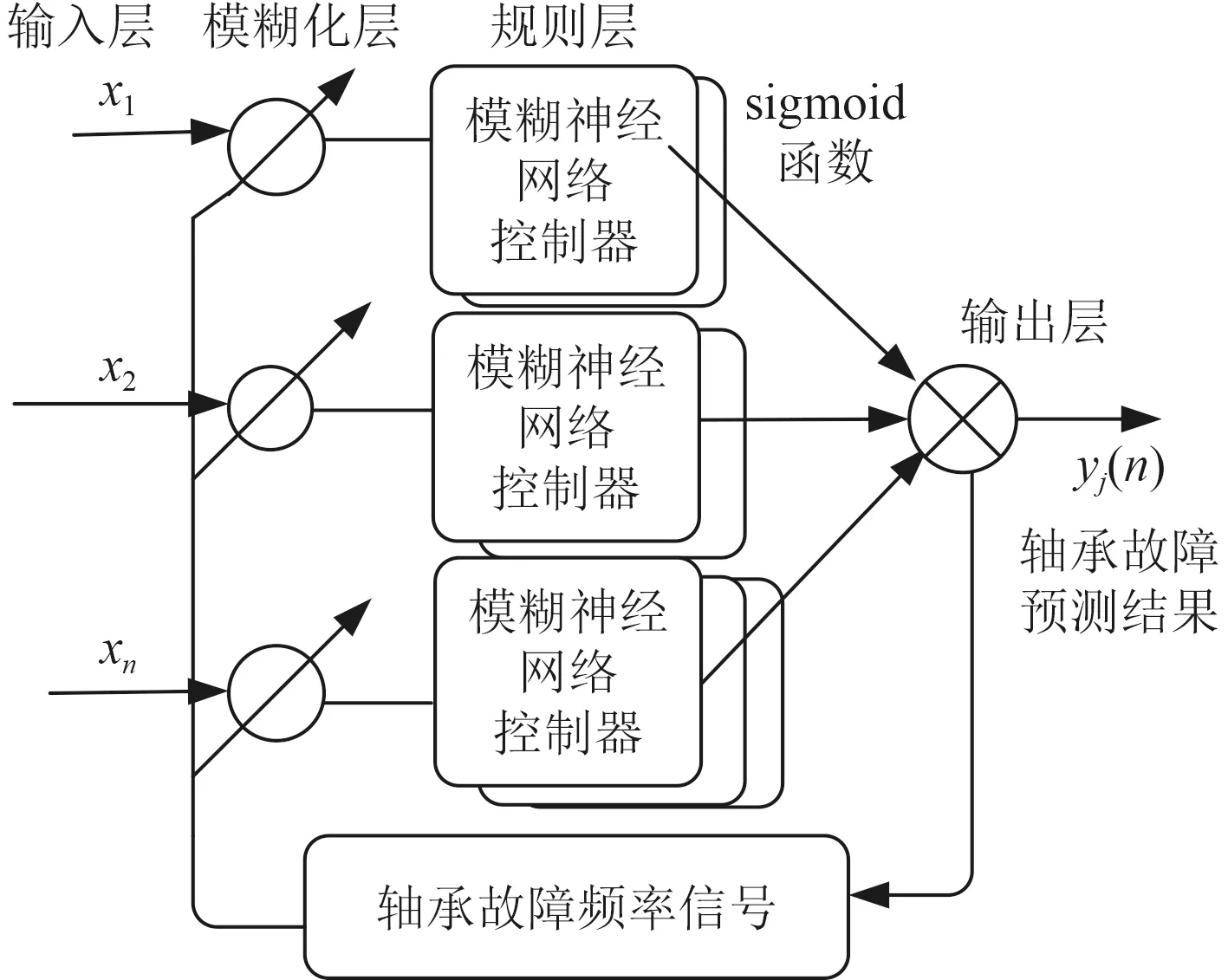
圖4 基于神經網絡和VMD 的軸承故障預測原理Fig.4 Bearing failure prediction principle based on neural network and VMD

基于模糊神經網絡和VMD 的軸承故障預測步驟如下：

步驟1 網絡的初始化。

步驟2 輸入信號的小波變換。

輸入信號為軸承振動信號x(t)，信號的頻域函數x(ω)滿足前述條件：

步驟3 神經元的距離計算，如下式：

式中，wi(t)為神經網絡的函數權值。

步驟4 故障預測。

建立系統的故障預測模型為：

式中： ωj(n) 為節點權值，aj為模糊因子，bj為變換因子。

2.4 船舶軸承故障預測系統的測試

為了驗證本文提出的故障預測方法的有效性，搭建船舶軸承的故障預測測試平臺，如圖5 所示。

圖5 船舶軸承的故障預測測試平臺Fig.5 Failure prediction test platform for ship bearings

測試平臺包括電源輸入、聯軸器、滑動軸承、轉速顯示單元、負載控制、變速驅動電機[4]等。

設定電機轉速2 000 r/min，采樣頻率20 kHz，時間歷程1 200 s，得到軸承故障頻譜如圖6 所示。

圖6 軸承故障頻譜Fig.6 Spectrum of bearing failures

可知，在1 000 s 左右出現明顯的故障頻率，振動幅值明顯增加。

3 結 語

針對船舶軸承的運行可靠性，本文結合模糊神經網絡和VMD 模態分解算法，從軸承的故障頻率建模出發，建立了船舶軸承的故障預測和診斷系統，并通過試驗臺測試驗證了方法的有效性。