基于BP 神經網絡的磁異常向下延拓方法
鐘 煬,劉 輝
(昆明船舶設備研究試驗中心, 云南 昆明 650001)
0 引 言
磁異常場作為艦船、潛艇等目標的固有物理場,包含豐富的目標特征信息[1–2],但水上磁異常測量成本高、效率低,常采用航磁測量的方法測量水上及水下目標的磁異常。現有的磁異常數據延拓方法延拓深度有限,無法充分利用航磁測量數據。航磁測量具有施工效率高、成本低、探測范圍大等諸多優點,其探測到的場值是由探測點位以下所有場源形成的疊加場,即每一個測點數據中都包含若干個場源的信息[3–4]。一般的航磁測量中只會測量獲得某條測線或某個觀測面內的數據,為節約探測時間成本,其他區域的磁異常數據只能依賴于對已知數據的空間轉換。因而磁異常數據的空間轉換在航磁測量中的作用非常重要,準確高效的磁場數據轉換是資料處理中的重要環節,能夠擴展數據內涵,突出目標,一定程度上減少探測結果的多解性,有效降低后續資料解釋的難度,是航磁數據處理中的重要環節[5]。
磁法勘探中的位場數據空間轉換方法包含向上延拓和向下延拓,向上延拓方法在數學上屬于狄里希萊問題,是一個適定問題,具有唯一且穩定的解,在實際計算中只要保證參與計算的點足夠多,便能夠得到準確的結果[6]。但向下延拓是一個不適定問題[7–8],無法直接求解,國內外諸多學者針對這一問題提出了多種解決方法。早在20 世紀40 年代,Evjen[9]采用Taylor 級數方法進行位場數據的解析延拓,其后Peters利用該方法推導出向下延拓公式。1958 年,Dean[10]利用傅里葉變換,首次將空間域中無法直接求解的向下延拓問題引入到頻率域中,并推導出頻率域中的延拓算子,但該方法僅能進行2 倍點距的下延[11]。2002 年,Fedi[12]提出了向下延拓的 ISVD(integrated second vertical derivative)法,該方法是指在進行 Taylar 級數展開時,奇數階和偶數階垂向導數采用不同求解方法,奇數階先求解垂向積分,再利用 Laplace 方程進行求解,而偶數階直接利用Laplace 方程求解,該方法能夠穩定地進行5 倍點距的下延。2006 年,徐世浙[13–14]提出了積分迭代的位場延拓方法,該方法通過將不穩定的向下延拓問題轉換為穩定的向上延拓問題,提高了延拓的最大深度,有效延拓深度可達20 倍數據點距,該方法是目前最常用的位場數據延拓方法之一[15]。但多次迭代的方法影響計算速度,而迭代次數過少影響計算延拓精度,而且這一方法會在一定程度上放大噪聲信號[16–17]。
本文提出一種基于BP 神經網絡的磁異常數據延拓方法,并構建由球體和長方體組成的混合模型。經模型試驗驗證,發現該方法延拓精度高,抗干擾能力強,能夠有效解決向下延拓中計算不穩定的問題。
1 位場數據向下延拓數學模型
位場數據向下延拓問題在數學上是一種不適定問題,作為現代地球物理學中最早利用數學原理解釋資料的方法之一,國內外諸多學者曾對位場數據向下延拓原理做過深入全面的分析,向下延拓具有完善的數學理論基礎。
位場的延拓問題實質上是求解式(1)中的柯西問題:

根據式(2)向上延拓公式反求解uh的過程即為位場數據的向下延拓問題,因此,可將式(1)的柯西問題改寫為:

通過傅里葉變換可將時域中的褶積問題轉換為頻域中的乘積問題,因此,頻域中的磁異常向下延拓問題可表示為:

采用快速傅里葉變換直接求解、積分迭代、奇異值分解等方法對其進行數值求解,在理論上可以進行10~20 倍點距的向下延拓。但對于更多倍點距的延拓問題,或在信噪比較低的情況下,這類方法會出現延拓結果失真嚴重的問題。
2 基于BP 神經網絡的磁異常向下延拓方法
BP 神經網絡是當前最為常用的多層前饋神經網絡,具有強大的學習和糾錯能力。當學習樣本充足且準確時,對于復雜非線性問題能夠將誤差控制在足夠小的范圍內。BP 神經網絡包括輸入層、隱含層和輸出層3 種結構,當問題較為復雜時,隱含層可以包含多層,其拓撲結構如圖1 所示。

圖1 BP 神經網絡拓撲結構圖Fig.1 Topological structure of BP neural network
BP 神經網絡的學習過程包括信號正向傳播和誤差反向傳播2 個部分,首先通過輸入層獲取原始學習樣本,數據經過隱含層建立激活函數,并獲取對應權值,最后經輸出層輸出結果。相鄰兩層間的傳遞公式如下式:
式中:x為輸入信號,ω為權值,a為偏置,f表示神經網絡中的激活函數,y表示數據在本層的輸出,也就是下一層的輸入。數據在神經網絡中傳播一輪后,計算誤差,對比預先設定的期望結果,若不滿足期望,將誤差由輸出層反向傳播至隱含層,其誤差傳遞函數為:
式中:μ為學習率,E為代價函數,通過上述誤差傳遞函數修正神經網絡中的權值和偏置,直至滿足期望。在計算過程中,為了獲取更接近真實問題的神經網絡模型,往往需要進行多次的迭代。
基于BP 神經網絡的磁異常數據延拓方法主要包括如下步驟:
步驟1 樣本數據輸入。樣本數據質量是影響BP 神經網絡計算結果的重要影響因素。為保證神經網絡中數據的準確性和質量,以球體、圓柱體、長方體理論模型在不同高度處的坐標、磁異常及其垂向一階導數作為樣本數據。
步驟2 數據歸一化。由于輸入數據中包含多種不同單位、量級的參數,為避免較大量級的參數吞沒較小量級參數的權重,使激活函數飽和而無法準確獲取神經網絡模型,需將輸入數據進行歸一化處理。輸入樣本的歸一化是將各組輸入數據數值映射到特定范圍內,本文方法是將其映射到[-1,1]的區間內。
步驟3 建立神經網絡模型。利用BP 神經網絡進行位場數據下延在神經網絡的應用中實際上算是一個較為簡單的問題,并且由于數據樣本來源于理論模型,具有很高的精度和準確性,不需要數十萬甚至上百萬數量級的樣本數據,僅需要包含單個隱含層的3 層BP 神經網絡即可進行計算。
步驟4 多次訓練獲取最優結果。由于BP 神經網絡在訓練及計算過程中的參數是隨機生成的,多次訓練和計算的結果一般不相同,為獲取較為準確的計算結果,取多次計算結果的均值作為最終輸出結果。
3 理論模型
為驗證磁異常數據向下延拓算法的準確性,選取球體與長方體組合模型驗證,各模型體平面分布如圖2所示。
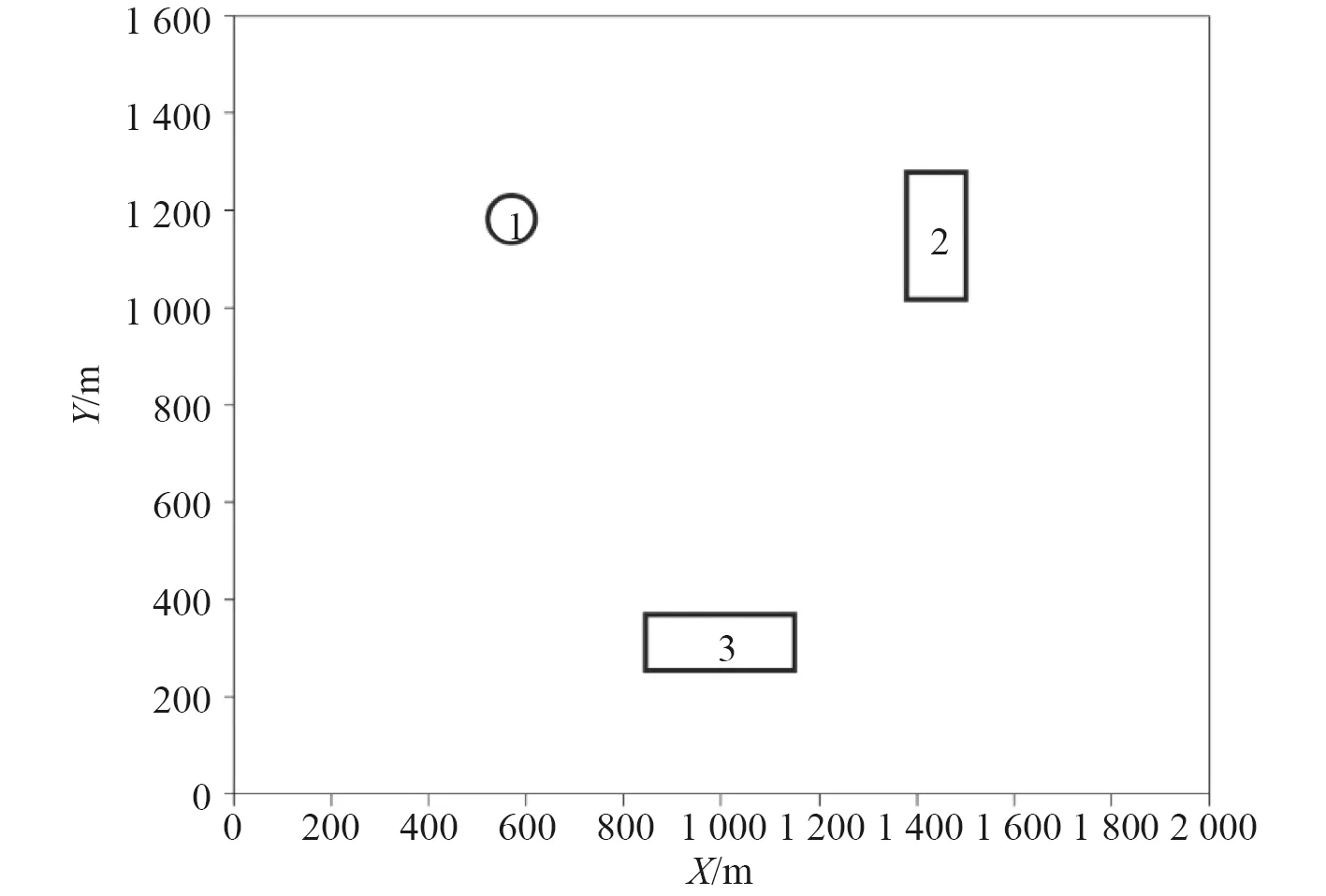
圖2 場源平面位置圖Fig.2 Field source plane location diagram
該模型由1 個球體和2 個長方體組成,在北東地空間直角坐標系中,其幾何參數見表1。

表1 各模型體幾何參數表Tab.1 The geometric parameters of each model body
3 個模型體磁化率為0.03 SI,磁化傾角均為60°,磁化偏角均為30°,地磁場強度為56 000 nT。所選測區x方向范圍為(0,2 000 m),y方向范圍為(0,1 600 m),測網間距為10 m×10 m。運用球體和長方體正演公式進行計算[18–19],公式如下:

所選模型體在距地面0 m 和300 m 處的磁異常如圖3 所示。
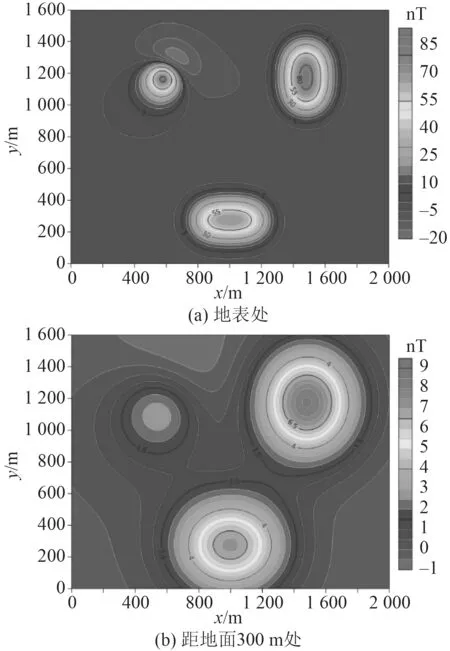
圖3 理論模型在0 m 和300 m 高度處磁異常等值線圖Fig.3 The contour map of the magnetic anomaly at the height of 0 m and 300 m in the theoretical model
4 方法驗證
以圖3(b)所示磁異常作為原始數據,分別運用積分迭代法和BP 神經網絡方法將磁異常數據延拓30 倍點距至地表處,結果如圖4 所示。
其中,積分迭代法最大迭代次數選取為500,每次迭代計算步長為0.01。對比兩圖,BP 神經網絡方法具有更準確的量級,且磁異常形態與理論磁異常圖3(a)更加接近。圖4(a)中球體模型磁異常在下延過程中產生畸變,負異常部分模糊不清。為進一步對比2 種方法延拓結果,截取模型2 中心點處,即y=1 175 m的剖面,2 種方法延拓結果如圖5 所示。
可知,虛線所示的BP 神經網絡方法更加接近理論磁異常值。當測量數據準確,信噪比較高的情況下,BP神經網絡具有比積分迭代方法更穩定的下延結果,并且能夠在保證數據精度的前提下穩定下延30 倍點距。
在實際磁異常探測時,環境磁噪聲的干擾較大。對于向下延拓問題,低信噪比的信號會導致磁異常值不連續,影響向下延拓結果。為模擬實際采集到的磁異常數據,在距地面高度300 m 處的磁異常數據中加入圖6(a)所示的高斯白噪聲,噪聲峰值為0.5 nT,加入噪聲后的磁異常等值線圖如圖6(b)所示。

圖6 含噪磁異常數據的向下延拓Fig.6 Downward continuation of noisy magnetic anomaly data
依舊運用上述2 種方法將含0.5 nT 高斯白噪聲的磁異常數據向下延拓至地表處,保持原有計算參數不變,運用積分迭代法計算結果如圖6(c)所示,運用BP 神經網絡方法的延拓結果如圖6(d)所示。對比可知,2 種方法延拓結果均不存在較嚴重的畸變,能夠分離3 個模型磁異常。仍然截取模型2 中心點所在的y=1 175處的截面,2 種延拓方法結果如圖7 所示。
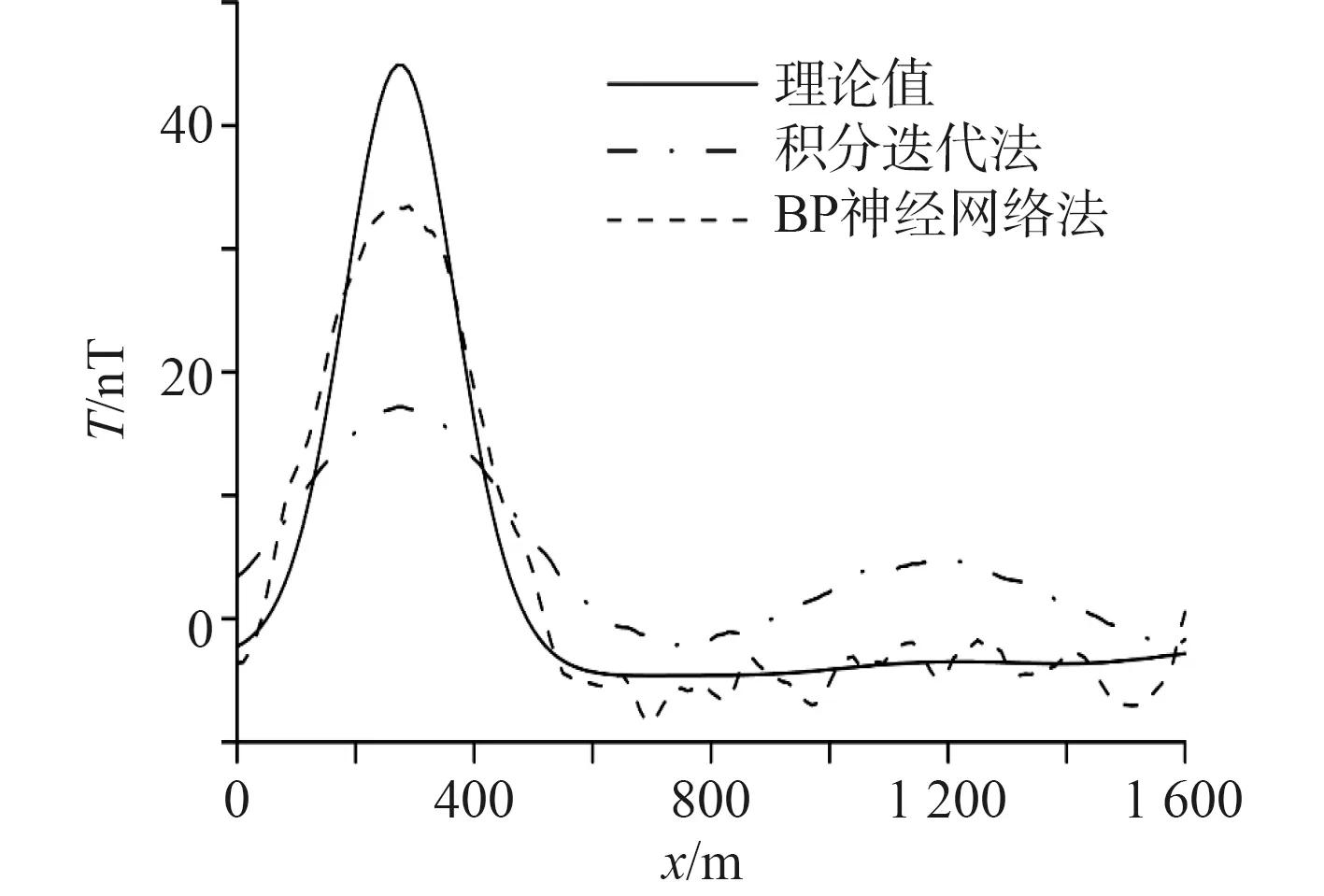
圖7 y=1 175 m 延拓結果磁異常剖面圖Fig.7 Magnetic anomaly profile of extension results at y=1 175 m
圖中,總體上虛線所示的BP 神經網絡方法延拓結果更貼近理論磁異常值,但在曲線右側具有稍大的波動。BP 神經網絡方法的延拓結果具有更接近真實地表磁異常值的量級,且磁異常大小形態也更接近于理論地表處的磁異常,但含有稍多的噪聲。
為直觀對比2 種方法延拓精度,假設理論模型磁異常值為xt,運用向下延拓方法計算的磁異常值為xc,則延拓結果的均方誤差為:

2 種方法延拓誤差如表2 所示。
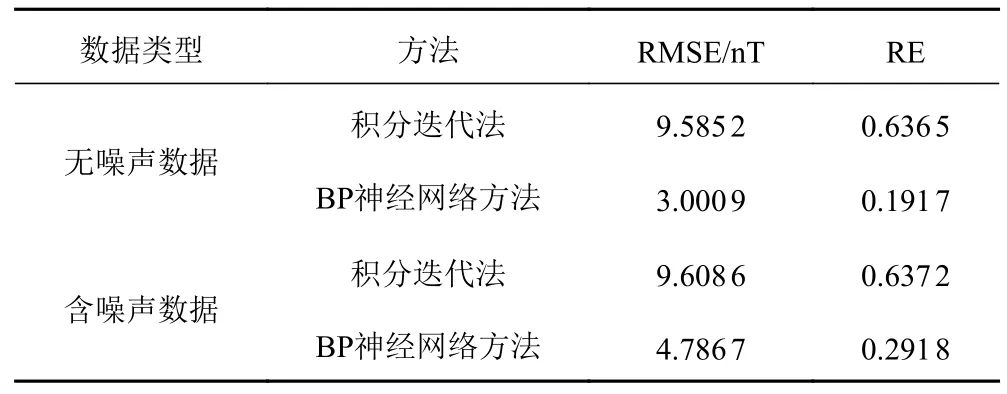
表2 積分迭代法與BP 神經網絡方法的均方誤差和相關性誤差表Tab.2 Mean square error and correlation error table of integral iteration method and BP neural network method
可知,無論是無噪聲的數據還是含噪聲的數據,BP 神經網絡方法均具有更小的誤差,該方法能夠穩定延拓30 倍點距。
5 結 語
本文研究意義在于將實測航磁數據向下延拓至海平面高度,代替船測磁異常數據,彌補船測磁異常測量效率低、成本高等缺點。有效解決了現有磁異常向下延拓方法有效延拓高度不足,強行進行20 倍以上點距延拓畸變嚴重的問題
1)提出基于BP 神經網絡的向下延拓方法,構建由球體和長方體組成的混合模型,通過球體及長方體磁異常正演公式計算不同高度處的磁異常理論數據,采用當前較常用的積分迭代法,對比本文提出的BP 神經網絡方法。結果表明,基于BP 神經網絡的向下延拓方法具有更加準確的結果,能夠進行30 倍點距的穩定下延。
2)模型試驗中,BP 神經網絡方法在高質量信號的條件下具有很好效果,能夠進行多倍點距下延,但仍存在一些問題。當信號中噪聲較強時,本身磁場信號較弱的區域會存在干擾,這部分區域的延拓結果并不理想,后續將針對這一問題開展研究。

