基于BWO 優(yōu)化VMD 和奇異譜熵的滾動軸承故障診斷

陳桂平，路曉鵬，劉婷婷

（1.柳州鐵道職業(yè)技術(shù)學(xué)院，廣西 柳州 545616；2.柳州職業(yè)技術(shù)學(xué)院，廣西 柳州 545616）

0 引言

滾動軸承是旋轉(zhuǎn)機械的關(guān)鍵部件，其狀態(tài)的好壞關(guān)乎設(shè)備整體的正常運行和安全，因此，對滾動軸承進行實時、正確的狀態(tài)識別與診斷極端重要。滾動軸承的故障特征在信號中以周期脈沖的形式存在，將周期脈沖成分從故障信號中提取出來是進行滾動軸承故障診斷的前提。對此，相關(guān)科研工作者開展了一系列的研究，并提出了多種提取信號特征的分解方法。小波變換（Wavelet Transform，WT）是一種經(jīng)典的信號分解方法，已被廣泛應(yīng)用于軸承故障信號的分解，然而WT 的噪聲魯棒性并不高，還需要人為選擇小波函數(shù)[1]。經(jīng)驗?zāi)B(tài)分解（Empirical mode decomposition，EMD）一經(jīng)提出就已被大量用于滾動軸承的故障分析中，但是EMD 存在端點效應(yīng)、模態(tài)混疊等問題，此外遞歸分解會導(dǎo)致分解誤差的積累[2]。針對EMD 端點效應(yīng)和模態(tài)混疊等問題，Smith[3]于2005 年提出了局部均值分解（Local Mean Decomposition，LMD），LMD 雖然避免了過包絡(luò)，端點效應(yīng)和模態(tài)混疊也得到了改善，但是遞歸分解仍然會導(dǎo)致誤差的累積。雖然WT、EMD 和LMD 不斷地有改進方法被提出，但是這些方法并不能很好地提取故障信號中的周期脈沖[4-6]。

變分模態(tài)分解（Variational Mode Decomposition，VMD）是由Konstantin[7]提出的信號處理方法，采用非遞歸求解變分模態(tài)方式，求解分量的帶寬和頻率中心，自適應(yīng)地對非平穩(wěn)信號進行分解，能較好地應(yīng)對模態(tài)混疊，此方法一經(jīng)提出，就受到了國內(nèi)外研究者的廣泛討論。但VMD 分解需要手動選取分解分量K和懲罰參數(shù)的值。如果參數(shù)選取不當，會影響到信號的分解效果。因此，針對VMD 超參數(shù)選取的問題，唐基貴等[8]提出以分解模態(tài)最小包絡(luò)熵為目標函數(shù)，采用PSO 算法優(yōu)化VMD 超參數(shù)；王衛(wèi)玉等[9]則提出以分解分量能量之和與原始信號能量之間的最小誤差為目標函數(shù)，采用GSA 算法優(yōu)化VMD 超參數(shù)；鄭義等[10]則以最大相關(guān)峭度為目標函數(shù)，采用GOA 算法優(yōu)化VMD 超參數(shù)。以上方法，對參數(shù)優(yōu)化后的VMD分解都能達到預(yù)期的分解效果。

本文提出了以分解模態(tài)最小包絡(luò)熵為目標函數(shù)，采用白鯨優(yōu)化算法（Beluga Whale Optimization，BWO）優(yōu)化VMD 超參數(shù)進行變分模態(tài)分解，并以分解得到的最小包絡(luò)熵的模態(tài)分量求取其奇異譜熵值作為特征向量數(shù)據(jù)集，最后利用SVM 訓(xùn)練、識別數(shù)據(jù)集實現(xiàn)滾動軸承的故障診斷。仿真結(jié)果表明，BWO 優(yōu)化VMD 和奇異譜熵的特征提取方法能夠有效地對滾動軸承故障進行診斷。

1 基本原理

1.1 白鯨優(yōu)化算法

白鯨優(yōu)化算法是Zhong C 等人根據(jù)白鯨的種群行為啟發(fā)而提出的優(yōu)化算法[11]。算法包含探索、開發(fā)和鯨落三個階段。

由條白鯨組成的種群可以用矩陣表示如下：

那么，所有白鯨的適度函數(shù)可以表示為：

在式（1）（2）中，d為待優(yōu)化變量的維數(shù)，n為種群數(shù)量，f為適應(yīng)度關(guān)系。

探索階段，搜索代理的位置由一對白鯨的游泳決定，白鯨的位置更新如下：

其中，t為當前迭代次數(shù)是第i條白鯨在第j維的新位置，和是第i和第r條白鯨（r為隨機）的當前位置，r1和r2是（0，1）的隨機數(shù)。sin（2πr2）和cos（2πr2）是用于平均魚鰭之間的隨機數(shù)。

開發(fā)階段，在BWO 的開發(fā)階段引入了Levy 飛行的策略捕捉獵物，其捕食的數(shù)學(xué)模型表示為：

其中，u和v是正態(tài)分布的隨機數(shù)，β是默認為1.5 的常數(shù)。

鯨落階段，白鯨的位置更新模型為：

其中，r5、r6和r7是（0，1）之間的隨機數(shù)，Xstep=（ub是鯨魚墜落的步長，C2= 2Wf×n為步長因子，ub和lb為變量的上界和下界。鯨魚墜落的概率Wf被設(shè)計為線性函數(shù)：

鯨魚墜落的概率從初始迭代的0.1 下降到最后一次迭代的0.05。

1.2 變分模態(tài)分解

VMD 算法是一種非遞歸的自適應(yīng)信號分解方法，其分解過程包括變分問題構(gòu)造和求解過程。實現(xiàn)的過程是利用自適應(yīng)的準正交變換將信號通過非遞歸方式分解為K個有限帶寬的固有模態(tài)分量uk。算法理論中的uk是具有有限帶寬的本征模態(tài)函數(shù)IMF，以ωk為中心頻率進行波動，帶寬通過對信號進行平滑估計獲得，其變分問題可以表示為：

上式中，{uk} = {u1，…，uk}表示變分分解后K個模態(tài)分量，{ωk} = {ω1，…，ωk}為模態(tài)分量的中心頻率，f（t）為原信號，δ（t）為狄拉克函數(shù)，?t為求偏導(dǎo)，[δ（t）+]*uk（t）為uk（t）的Hilbert 譜。

用拉格朗日算子λ（t）和二次懲罰因子α將（8）式中的目標函數(shù)約束優(yōu)化轉(zhuǎn)化為無約束的優(yōu)化問題，確保約束條件的嚴格性和信號重構(gòu)精度。表達式如下：

采用交替方向乘子法迭代更新{uk}，{ωk}和λ，求取（9）式中的鞍點，即為（8）式的最優(yōu)解。

算法的自適應(yīng)實現(xiàn)過程如下[7]：

（2）n = n+ 1，執(zhí)行整個循環(huán)；

（3）k = k+ 1，直到k = K，執(zhí)行公式（9）迭代更新uk；

執(zhí)行公式（10）迭代更新ωk；

（4）執(zhí)行公式（11）迭代更新λ；

（5）根據(jù)各模態(tài)和中心頻率不斷循環(huán)更新，重復(fù)執(zhí)行步驟2）～4），直到滿足收斂條件＜ε，實現(xiàn)信號自適應(yīng)分解為K個中心頻率不重疊的模態(tài)分量。

1.3 奇異譜熵

奇異譜分析常用于分析和預(yù)測非線性時間序列，它能分析時間序列具有的潛在結(jié)構(gòu)。奇異譜熵（Singular Spectral Entropy，SSE）則是一種基于奇異譜分析和信息熵分析相結(jié)合的分析方法[12]。奇異譜熵算法的原理如下：

對于長度為N的一維時間序列[x1，x2，…，xN]，選擇合適的窗口長度L（一般要求L＜），將時間序列進行時間延時τ= 1 的滯后排列得到L × K的軌跡矩陣：

然后對X進行奇異值分解，其分解形式為：

其中，U和V均為單位正交矩陣，U稱為左奇異矩陣，V稱為右奇異矩陣，ΣL×K=diag（σ1，σ2，…，σL）為奇異值。

奇異值反映了對應(yīng)的奇異矩陣對原信號序列的能量貢獻，奇異值大表示包含的有效信息多。得到信號的奇異值譜{σi}后，對每個奇異值進行概率密度計算，即，參照Shannon 熵的概念，可以求得該信號的奇異譜熵為：

以上分析可以看出，奇異譜熵SSE 是對時間序列經(jīng)奇異譜分解后的潛在結(jié)構(gòu)的定量描述，一定程度上可以反映信號能量的分布情況。時間序列的能量越大，得到的奇異譜熵值就會越大，反之則越小。

2 軸承信號預(yù)處理

借助凱斯西儲大學(xué)的滾動軸承試驗數(shù)據(jù)進行驗證分析。選取試驗中驅(qū)動端的SKF-6205-RS JEM 深溝球型軸承，電機負載為1 HP、轉(zhuǎn)速為1772 r/min 和采樣頻率為12 kHz 的采樣信號，分別選取直徑0.1778 mm、深度0.2794 mm 電蝕故障尺寸下的內(nèi)圈、滾動體、外圈軸承和同樣載荷、轉(zhuǎn)速和采樣頻率下的正常軸承四種信號作為實驗對象。

2.1 BWO 優(yōu)化VMD 參數(shù)

VMD 分解時，需要先確定分解模態(tài)個數(shù)K和懲罰參數(shù)α。文獻[13]指出，這兩個參數(shù)的選取會影響到分解結(jié)果，懲罰參數(shù)α影響去噪效果和細節(jié)保留度，α越小，得到的各模態(tài)分量帶寬越大，反之，α越大各分量帶寬越小。至于模態(tài)個數(shù)K，信號分解模態(tài)數(shù)太少時，容易造成原始信號中的重要信息特征丟失，而分解模態(tài)數(shù)太多時，會造成鄰近模態(tài)的中心頻率接近，形成頻率混疊。VMD 分解效果受模態(tài)分量數(shù)量和懲罰因子的影響，因此，采用BWO 算法對分解參數(shù)α和K進行優(yōu)化，并以分解模態(tài)分量的最小包絡(luò)熵為目標函數(shù)。BWO 優(yōu)化VMD 參數(shù)的過程中4 種工況最小包絡(luò)熵的迭代過程，如圖1 所示。最終得到的最優(yōu)分解參數(shù)α和K值以及各模態(tài)的包絡(luò)熵見表1。

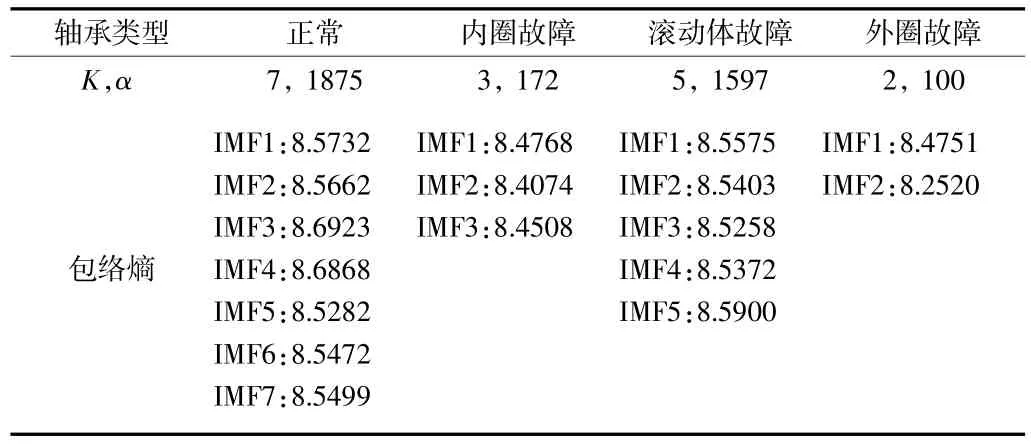
表1 BWO 優(yōu)化VMD 參數(shù)值及各模態(tài)包絡(luò)熵

圖1 BWO 優(yōu)化VMD 最小包絡(luò)熵的迭代過程

根據(jù)熵的概念，對于信號來說，包絡(luò)熵可以表示信號的稀疏特性，信號中噪聲較多時，說明特征信息較少包絡(luò)熵值較大，反之，則說明包絡(luò)熵值較小。對分解得到的模態(tài)信號依次計算每個模態(tài)信號在該組分解信號集中的包絡(luò)熵值，并選擇熵值較小的一組模態(tài)分量作為后續(xù)的處理信號。因此，對四種工況的軸承的原始信號和VMD 分解得到的最小包絡(luò)熵的模態(tài)分量及其包絡(luò)譜如圖2 所示。

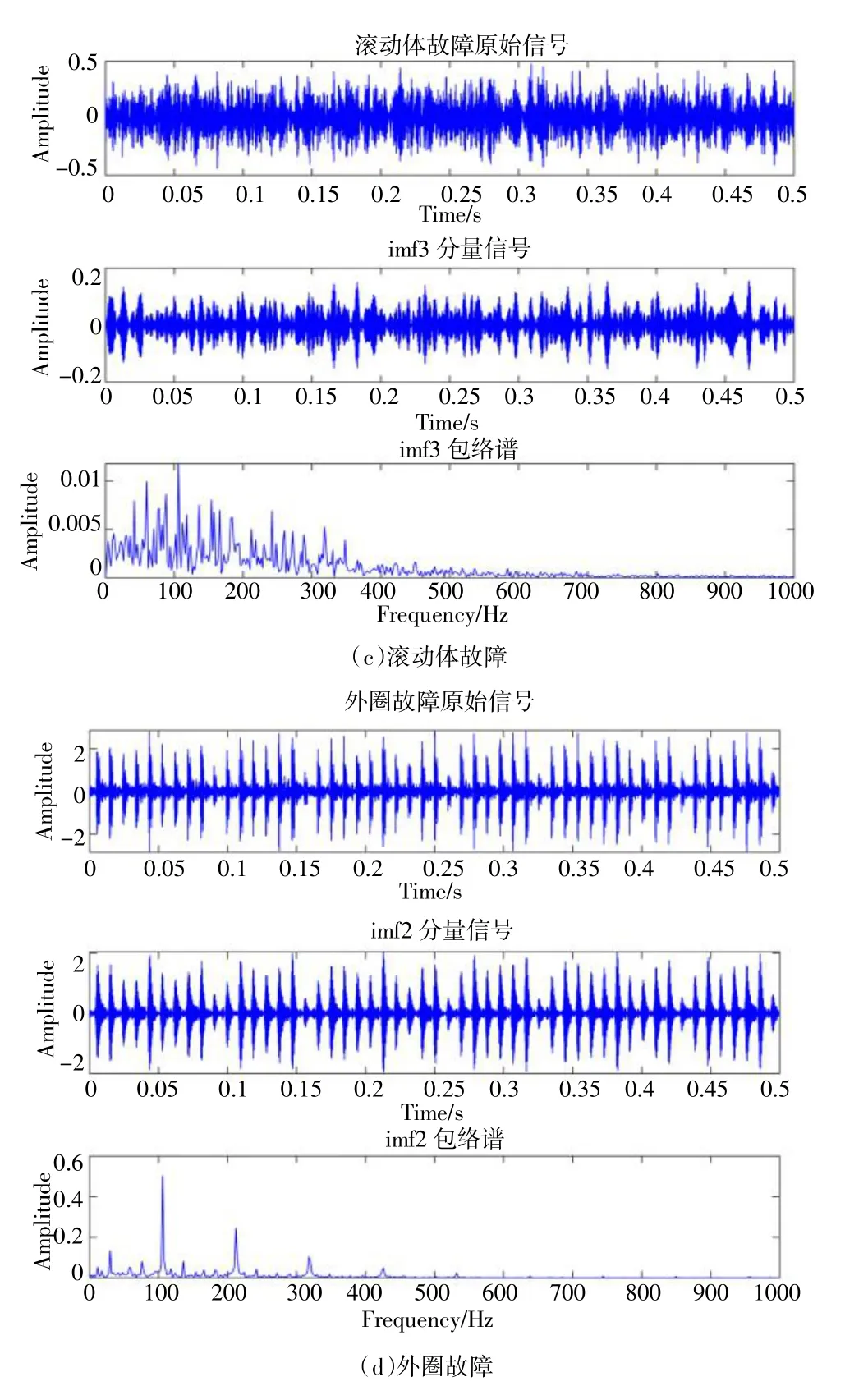
圖2 四種工況軸承原始信和最小包絡(luò)熵的分量及其包絡(luò)譜

2.2 奇異譜熵的計算

對于電機轉(zhuǎn)速為1772 r/min 和采樣頻率為12 kHz的采樣信號，可以計算出電機每旋轉(zhuǎn)1 圈，約產(chǎn)生406 個采樣點。為了簡化計算，將電機1 個旋轉(zhuǎn)周期內(nèi)的采樣點等分為4 份，即可得到4 段時間序列，分別計算奇異譜熵，得到4 個奇異譜熵值。為了完整揭示一個旋轉(zhuǎn)周期內(nèi)4 段時間序列奇異譜熵的變化趨勢，處理時，將旋轉(zhuǎn)范圍取到5/4 圈，即每5 個奇異譜熵值為一個特征向量。從理論上來說，第1 個奇異譜熵的值和第5 個奇異譜熵的值是相等的。

分別對正常、內(nèi)圈故障、滾動體故障、外圈故障四種工況軸承的振動信號進行滑窗取樣，每次取樣窗口是510 個數(shù)據(jù)，每次滑動的長度是406 個數(shù)據(jù)，對取樣窗口的數(shù)據(jù)進行VMD 分解，將包絡(luò)熵值最小的一組模態(tài)分量分為5 個時間序列，分別進行奇異譜熵計算，即可得到5 個奇異譜熵值為一組的一個特征向量。每種工況信號滑窗取樣200 次，則每種工況可以得到200 組特征向量。

經(jīng)VMD 處理后的每種工況得到的200 個特征向量的平均值如圖3 所示。圖中每種奇異譜熵值變化的趨勢可以反映出該信號的能量波動趨勢，可以以此來表示特征，它們之間的趨勢差別越大越有利于診斷識別。此外，圖中第1 個奇異譜熵值的大小和第5 個奇異譜熵值的基本上是相等的，這也驗證了前面的猜想。圖4 所示為四種工況原始信號的包絡(luò)譜熵均值的特征向量圖，圖中滾動體故障和外圈故障的后三個熵值趨勢比較相似，將會影響正確的診斷識別，從側(cè)面也可以反映出經(jīng)VMD 處理后的四種工況的奇異譜熵的區(qū)分效果會更好。

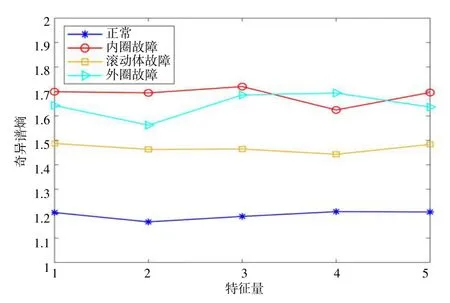
圖3 VMD 處理后四種工況的奇異譜熵值對比

圖4 原始信號四種工況的奇異譜熵值對比

3 故障軸承診斷

將每種工況的每5/4 轉(zhuǎn)動周期的5 個奇異譜熵作為一組特征向量，則可得到800 組特征向量。將800 組數(shù)據(jù)樣本打亂，取70%作為訓(xùn)練樣本，剩下30%作為測試樣本。先用SVM 對訓(xùn)練樣本進行訓(xùn)練得到訓(xùn)練模型，再將測試樣本輸入到訓(xùn)練好的模型中進行診斷識別[14]。其得到的分類結(jié)果如圖5 所示，可以看出，采用BWO 優(yōu)化VMD 和奇異譜熵的特征提取方法，其軸承狀態(tài)準確率達100%。對原始信號直接進行奇異譜熵計算的SVM 識別結(jié)果如圖6 所示，可見采用奇異譜熵作為特征向量，有較好的識別效果，并且滾動體和外圈有部分誤識別的情況，這與前面的分析基本一致。

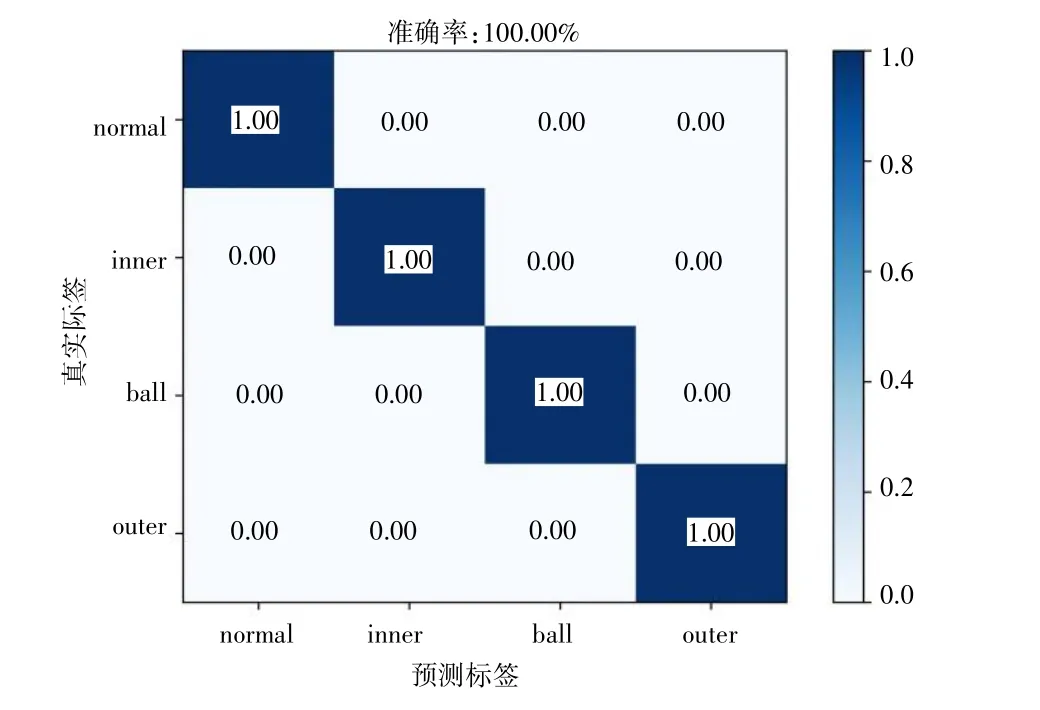
圖5 BWO-VMD+SSE 識別結(jié)果

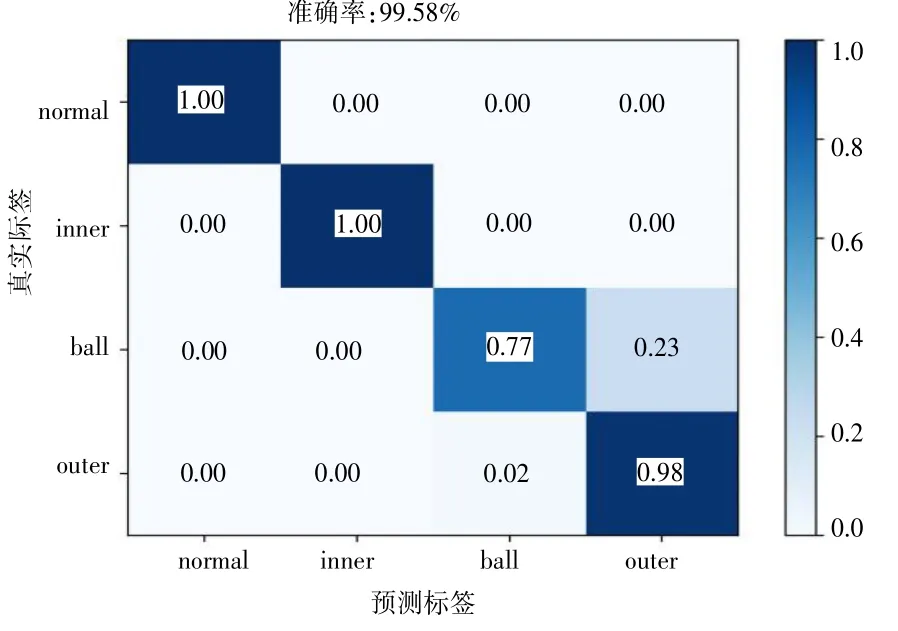
圖6 原始信號+SSE 識別結(jié)果

選用同樣的工況軸承信號，分別采用EMD、LMD進行信號分解，仍然選取分解得到其模態(tài)分量最小包絡(luò)熵的分量信號構(gòu)造特征向量，用SVM 對4 種工況軸承進行故障診斷，得到的分類結(jié)果如圖7、圖8 所示，由圖可見故障識別率依然很高。因此，信號分解得到的最小包絡(luò)熵的模態(tài)分量和奇異譜熵結(jié)合進行故障診斷具有較好的效果。

圖7 EMD+SSE 識別結(jié)果

圖8 LMD+SSE 識別結(jié)果

4 結(jié)語

結(jié)合滾動軸承故障振動周期性沖擊的特點，提出了一種基于BWO 優(yōu)化VMD 和奇異譜熵的特征提取方法，以信號在一個周期內(nèi)的奇異譜熵值的特征映射出故障脈沖的特點。

以VMD 分解模態(tài)分量的最小包絡(luò)熵為目標函數(shù)，用BWO 算法對VMD 的分解參數(shù)α和K進行優(yōu)化，并以最優(yōu)參數(shù)進行VMD 分解，對分解得到的最小包絡(luò)熵的模態(tài)分量求取奇異譜熵作為特征向量輸入SVM，可以準確實現(xiàn)滾動軸承的故障診斷。

采用BWO 優(yōu)化VMD 和奇異譜熵的故障特征提取方法在表達振動信號的復(fù)雜度時，能夠很好區(qū)分軸承的四種工況狀態(tài)，與EMD+SSE 和LMD+SSE 的特征提取能力相比，具有較好的診斷識別效果。