電磁感應現象中“桿+導軌”模型梳理
■河南省鄭州市第三十一高級中學 董衛剛 王夢娜
電磁感應現象中的“桿+導軌”模型是近幾年高考中的常見考點之一,比如2020年高考全國Ⅰ卷第21題、全國Ⅲ卷第24題,2021年高考全國乙卷第25 題、北京卷第7 題,2022年高考全國甲卷第20 題、遼寧卷第15題,2023年高考全國甲卷第25題、湖南卷第14題、遼寧卷第10 題等。涉及“桿+導軌”模型的物理試題幾乎涵蓋了高中物理所有的核心內容,綜合性較強,區分度較高。下面將涉及“桿+導軌”模型的物理試題進行系統梳理,總結求解此類問題的思路和方法,為同學們的復習備考提供參考。
一、電磁感應核心知識梳理
1.感應電流方向的判斷方法:
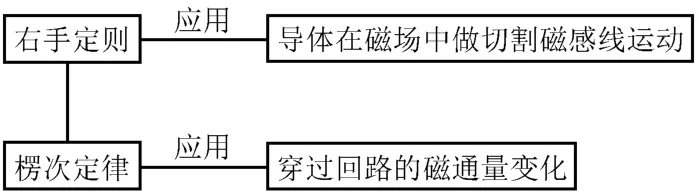
2.感應電動勢大小的求法:
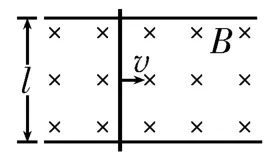
圖1
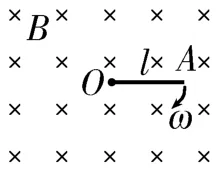
圖2
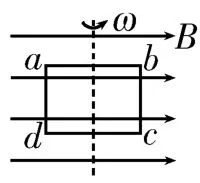
圖3
3.感應電荷量的計算:
4.動量定理在“桿+導軌”模型中的應用:
二、“桿+導軌”模型梳理
模型一:單桿,無電源,受恒定外力
如圖4 所示,金屬桿MN放在水平放置的光滑導軌上,空間存在垂直于導軌平面向上的勻強磁場,金屬桿MN受到恒定的外力作用。以金屬桿MN為研究對象,根據牛頓第二定律得,解得,因此隨著速度v的增大,加速度a逐漸減小,當a=0的時候,金屬桿MN達到平衡狀態,以恒定的速度做勻速直線運動。上述規律不僅適用于水平面內的運動,豎直平面內的運動或斜面上的運動也適用,只不過是將恒力稍微變化了一下。
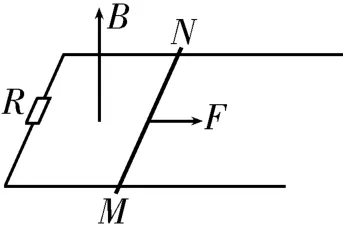
圖4
例1如圖5所示,兩根足夠長的光滑導軌豎直放置,間距為L,頂端接阻值為R的電阻。勻強磁場方向垂直于導軌所在平面(紙面)向里,磁感應強度為B,質量為m、電阻為r的金屬棒在距磁場上邊界某處由靜止釋放,金屬棒和導軌始終接觸良好。不計導軌的電阻,重力加速度為g,則下列說法中正確的是( )。
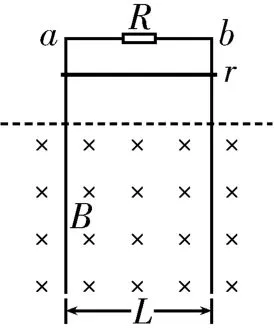
圖5
A.金屬棒在磁場中運動時,通過電阻R的電流方向為a→b
B.金屬棒剛進入磁場時一定做加速運動
C.金屬棒的速度為v時,金屬棒所受的安培力大小為
D.金屬棒以穩定的速度下滑時,電阻R的熱功率為
思路點撥:金屬棒進入磁場后,產生的感應電動勢E=BLv,回路中的感應電流,通過電阻R的電流方向為b→a,金屬棒所受的安培力大小,當金屬棒穩定下滑時,F=mg,電阻R的熱功率,解得。
答案:D
模型二:單桿,無電源,有初速度
如圖6 所示,給金屬桿ef一個初速度(初始沖量),讓金屬桿ef運動起來,金屬桿ef切割磁感線,在回路cbef中產生感應電流,金屬桿ef相當于電源,此時金屬桿ef受到一個與運動方向相反的安培力,阻礙金屬桿ef的運動,金屬桿ef做減速運動,速度減小會讓安培力隨著減小,加速度就跟著減小,因此金屬桿ef做加速度減小的減速運動,直到速度減為零,停止運動。若導軌是光滑的,則金屬桿ef的初動能全部轉化為電阻R產生的焦耳熱,即,金屬桿ef通過克服安培力做功把機械能轉化為了電能。同時還可以根據動量定理得,又有q=·Δt,求出在此過程中通過電阻R的電荷量。
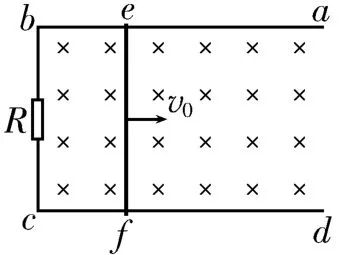
圖6
例2(2021年高考北京卷)如圖7所示,在豎直向下的勻強磁場中,水平U 型導體框左端連接一阻值為R的定值電阻,質量為m、電阻為r的導體棒ab置于導體框上。不計導體框的電阻、導體棒與框間的摩擦。導體棒以水平向右的初速度v0開始運動,最終停在導體框上。在此過程中( )。
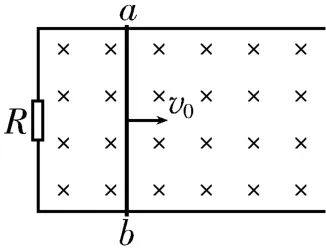
圖7
A.導體棒做勻減速直線運動
B.導體棒中感應電流的方向為a→b
C.電阻R消耗的總電能為
思路點撥:導體棒做加速度減小的減速運動,導體棒中感應電流的方向為b→a。安培力的變化會引起加速度的變化,根據能量守恒定律和動能定理可知,電阻R消耗的總電能為,導體棒克服安培力做的總功等于。
答案:C
模型三:單桿,有電容,受恒定外力
如圖8所示,水平放置的光滑平行導軌左側接電容為C的電容器,空間存在垂直于導軌平面向上的勻強磁場,金屬棒MN和導軌的電阻忽略不計,摩擦力不計,金屬棒MN在水平向右的恒定拉力F的作用下,由靜止開始做加速運動,持續對電容器充電,則存在充電電流時,有F-BIl=ma,,ΔQ=CΔU,ΔU=ΔE=BlΔv,整理得,其中,解得,因此金屬棒MN做加速度恒定的勻加速直線運動。從能量的角度分析,存在功能關系。
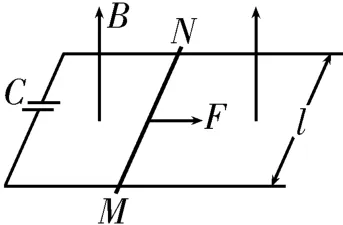
圖8
例3如圖9所示,間距為L的金屬導軌豎直平行放置,空間存在垂直于導軌所在平面向里的勻強磁場,磁感應強度為B,在導軌上端接一電容為C的電容器,一質量為m的金屬棒與導軌始終保持良好接觸。將金屬棒距地面高度為h處由靜止開始釋放,已知重力加速度為g,一切摩擦及電阻均不計。在金屬棒下滑至地面的過程中,下列說法正確的是( )。
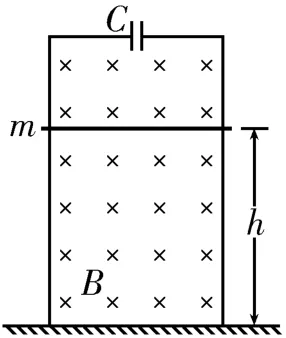
圖9
A.若h足夠大,則金屬棒最終勻速下落
B.金屬棒下滑至地面時,電容器儲存的電勢能為mgh
思路點撥:根據牛頓第二定律得mg-BIL=ma,又有,v=at,Q=It,解得,金屬棒在下降過程中做勻加速直線運動,金屬棒下滑至地面時的動能,又有,根據能量守恒定律得電容器儲存的電勢能。
答案:D
模型四:雙桿,等長,有初速度
如圖10所示,光滑導軌上放置兩根導體棒,給導體棒1 一個初速度,導體棒1受安培力的作用做加速度減小的減速運動,導體棒2受安培力的作用做加速度減小的加速運動,最后兩導體棒以相同的速度做勻速直線運動,對兩導體棒運用動量守恒定律可以求出最終的共同速度。從能量的角度分析,導體棒1動能的減少量=導體棒2 動能的增加量+焦耳熱。
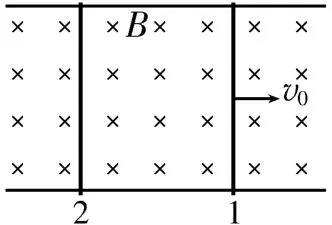
圖10
例4如圖11所示,兩根足夠長的平行光滑導軌固定在絕緣水平面上,所在空間存在方向垂直于水平面、磁感應強度為B、范圍足夠大的勻強磁場,導軌的間距為L,電阻不計;導軌上靜置兩根有效長度均為L的導體棒PQ和MN,其中導體棒PQ的質量為2m、阻值為R,導體棒MN的質量為m、阻值為2R。若在t=0 時刻給導體棒PQ一個平行于導軌向右的初速度v0,不計運動過程中兩導體棒的相互作用,則( )。
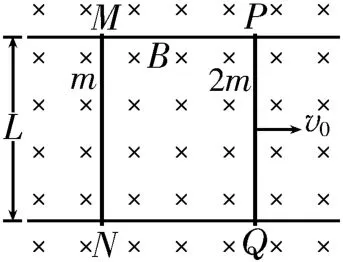
圖11
A.t=0 時刻,兩導體棒的加速度大小相等
B.t=0時刻,導體棒PQ兩端的電壓為
C.導體棒PQ勻速運動時的速率為
D.從t=0時刻到導體棒PQ勻速運動的過程中,導體棒MN中產生的焦耳熱為
思路點撥:導體棒PQ向右運動,產生的感應電動勢E=BLv0,此時路端電壓為,回路中的感應電流,兩導體棒受到的安培力大小均為F=BIL,則,因此t=0 時刻,兩導體棒的加速度大小不相等,受到的安培力大小相等,方向相反,兩導體棒在運動過程中滿足動量守恒定律,則2mv0=(m+2m)v共,最終兩導體棒以速度做勻速直線運動。兩導體棒中的電流相等,產生的焦耳熱分別為,則QMN∶QPQ=2∶1。根據能量守恒定律可知,在整個運動過程中產生的總熱量等于系統總動能的減少量,即,解得。
答案:BD
模型五:雙桿,等長,受恒定外力
如圖12所示,足夠長的光滑導軌上放置兩根導體棒,導體棒1 受到一個恒定的力F的作用,導體棒1 做加速度逐漸減小的加速運動,導體棒2做加速度逐漸增大的加速運動,最終兩導體棒以相同的加速度做勻加速直線運動,兩導體棒的速度差恒定,回路中存在恒定的感應電流,兩導體棒受到的安培力大小相等,對整體有F= (m1+m2)a,對導體棒2 有,聯立以上兩式可以求出兩導體棒的速度差值。從能量的角度分析,外力做的功=導體棒1的動能+導體棒2的動能+焦耳熱。
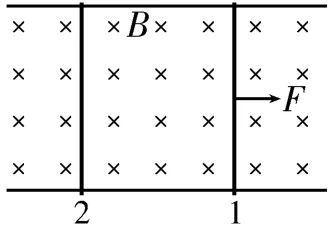
圖12
例5(2020年高考全國Ⅰ卷)如圖13所示,U 型光滑金屬框abcd置于水平絕緣平臺上,ab邊和dc邊平行,和bc邊垂直。ab、dc邊足夠長,整個金屬框的電阻可忽略。一根具有一定電阻的導體棒MN置于金屬框上,用水平恒力F向右拉動金屬框,運動過程中,裝置始終處于豎直向下的勻強磁場中,導體棒與金屬框保持良好接觸,且與bc邊保持平行。經過一段時間后( )。
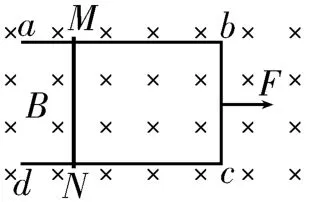
圖13
A.金屬框的速度大小趨于恒定值
B.金屬框的加速度大小趨于恒定值
C.導體棒所受安培力的大小趨于恒定值
D.導體棒到金屬框bc邊的距離趨于恒定值
思路點撥:金屬框向右的加速度與導體棒的加速度不同,同一時刻兩者速度也不同,設金屬框的質量為m1,速度為v1,導體棒的質量為m2,速度為v2,則回路中的感應電流,感應電流從0 開始增大,導體棒的加速度a2從零開始增大,金屬框的加速度a1從開始減小,二者的加速度差值減小,當a1=a2時,有F=(m1+m2)a,則恒定,根據F安=m2a可知,安培力不再變化,感應電流不再變化,金屬框與導體棒的速度差保持不變,但導體棒的速度小于金屬框的速度,則導體棒到金屬框bc邊的距離越來越大。
答案:BC
模型六:雙桿,不等長,有初速度
如圖14 所示,光滑導軌水平放置,勻強磁場垂直于水平面向下,左側導軌間距為L,右側導軌間距為2L,且兩側導軌均足夠長。現給金屬桿cd一水平向右的初速度v0,金屬桿cd做切割磁感線運動,產生感應電流,金屬桿cd受到的安培力阻礙它的運動,金屬桿ab受到的安培力使它做加速運動,兩金屬桿長度不同,所受安培力大小不相等,系統動量不守恒,一旦金屬桿ab開始運動,金屬桿ab也要做切割磁感線運動,產生一個反電動勢,使得回路中的感應電流減小,當感應電流為零時,兩金屬桿均做勻速運動,此時兩金屬桿的速度關系為vab=2vcd,分別對兩金屬桿應用動量定理可以求出最終的速度。
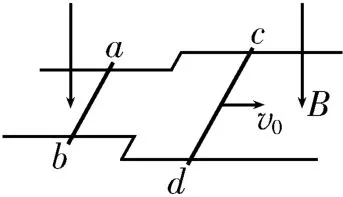
圖14
例6如圖15所示,光滑導軌水平放置,勻強磁場垂直于水平面向下,磁感應強度為B,左側導軌間距為L,右側導軌間距為2L,且兩側導軌均足夠長。質量為m的導體棒ab和質量為2m的導體棒cd均垂直于導軌放置,處于靜止狀態。導體棒ab接入電路的電阻為R,導體棒cd接入電路的電阻為2R,兩導體棒始終在對應的導軌部分上運動,并始終與導軌垂直且接觸良好, 導軌電阻不計。現瞬間給導體棒cd一水平向右的初速度v0,則對此后的運動過程,下列說法中正確的是( )。

圖15
A.兩導體棒組成的系統動量守恒
B.導體棒cd最終的速度為
C.整個過程中,通過導體棒cd的電荷量為
D.從導體棒cd獲得初速度到二者穩定運動的過程中,系統產生的焦耳熱為
思路點撥:因為導體棒ab和cd的長度不同,所以受到的安培力大小不相等,兩導體棒組成的系統動量不守恒。當導體棒ab和cd產生的感應電動勢大小相等時,兩導體棒都做勻速直線運動,則BLvab=B·2Lvcd,對兩導體棒分別應用動量定理得,解得。結合,解得。根據能量守恒定律得整個過程中系統產生的焦耳熱,解得。
答案:CD
總結:“桿+導軌”是一個經典的模型,涉及知識點比較多。在以“桿+導軌”模型為素材的電磁感應問題中,若滿足動量守恒條件,則應優先選用動量守恒定律列式求解;若已知位移,則需結合動能定理列式求解;若已知時間,則需結合動量定理列式求解;若需要求電荷量,則需要應用安培力的沖量I安=BLq,并結合能量守恒定律列式求解。總之,求解以“桿+導軌”模型為素材的電磁感應問題時,需要充分挖掘題目隱含條件,使復雜的問題簡單化,將難點逐個突破。

