基于多觀測隱非齊次HMM的光伏功率概率預測

馬 瓊，馬 雷，汪佐浩，張 浩

(1.國網臨夏供電公司，甘肅臨夏 731100；2.西安理工大學水利水電學院，陜西西安 710048)

光伏發電系統因其分布靈活、可靠性高的特點在推動電源結構清潔化進程中擁有較強的競爭力，是實現我國“碳達峰、碳中和”戰略目標及推動構建以新能源為主體的新型電力系統的重要支撐技術之一[1-2]。然而，光伏輸出功率較強的隨機性、間歇性與非平穩特性給光伏發電系統進一步的集成應用帶來巨大挑戰[3-5]。穩定可靠的預測技術對于電網適應高比例新能源接入與構建健全的電力系統風險防控機制具有重要意義。

傳統光伏功率預測的研究大都致力于建立輸出更接近預測對象真實測量值的確定性預測模型，即輸出預測對象未來某時刻的單點期望值[6]。然而，確定性預測結果缺乏對光伏發電功率不確定性信息的描述，使得能源系統設計規劃、電網調度、電力市場等場景決策者難以在實際工程實踐中做出最優決策。因此，需要更為全面的預測信息以在最大程度上提高實踐中應對光伏出力不確定性的能力。在這種情況下，概率預測理論開始逐漸得到關注。

概率預測是應對光伏出力高度不確定及可變性的一種解決方案，通過量化隨機過程不確定性，以概率密度、分位數、預測區間或綜合形式發布預測結果，提供待預測對象完整的概率統計信息。近年來，越來越多的光伏發電應用場景將能源不確定性納入決策制定的考慮范圍，如分布式能源系統設計規劃、能源管理系統(energy management system,EMS)優化調度、電力市場交易等，這就需要穩定、可靠、準確的功率概率分布信息提供數據支撐。概率預測在提高可再生能源占比、能源利用率及能源系統彈性性能中發揮重要作用。

概率預測方法按照采用模型的不同可分為物理方法、統計學方法、人工智能方法、組合方法等。劉潔等基于高階馬爾可夫鏈和高斯混合模型進行建模，計算得到光伏出力概率密度函數[8]。王開艷等基于氣象特征數據，采用模糊C 均值聚類方法進行相似日劃分，利用分位數回歸及卷積神經網絡(CNN)與雙向長短記憶神經網絡算法(BiLSTM)建立了QRCNN-BiLSTM 光伏功率短期概率預測模型[9]。盡管這些方法都取得了一定程度的效果，然而他們要么過于復雜難以在實踐中應用，要么基于一些在實際應用中難以驗證的假設。

隱馬爾可夫模型(hidden Markov model,HMM)基于少量非限制性假設，描述雙隨機過程非線性動力學特性，被廣泛應用于故障診斷、信號識別、氣象預測等領域[10]。由于光伏發電過程與氣象變化過程均為隨機過程，理論上只要確定狀態空間與觀測空間，便可使用HMM 很好地描述兩者的關系。同時，非齊次HMM 允許隱藏狀態受到相關協變量的作用，考慮了時間尺度的影響，能更好地描述研究對象與復雜作用因素關系。

鑒于此，本文提出基于多觀測非齊次HMM 的光伏出力概率預測模型。首先，介紹了傳統HMM 的基礎原理及多觀測非齊次HMM 的推導與基礎問題的求解。接著，引入百分比離散參數建立光伏出力及相關氣象參數離散有限集合，即建模所需的狀態空間與觀測空間。基于真實光伏電站運行數據建立出力概率預測模型，輸出未來各時刻點光伏出力概率分布信息。最后，通過與傳統HMM、單/多觀測非齊次HMM 模型、支持向量機模型(support vector machine,SVM)的比較對所提出模型的可行性與預測性能進行了分析驗證。

1 模型的構建

1.1 隱馬爾可夫模型

圖1 展示了隱馬爾可夫過程示意圖，st－1，st，st+1分別表示在t－1、t、t+1 連續時刻下狀態值，相對應的ot－1，ot，ot+1分別為各時刻下的觀測值。

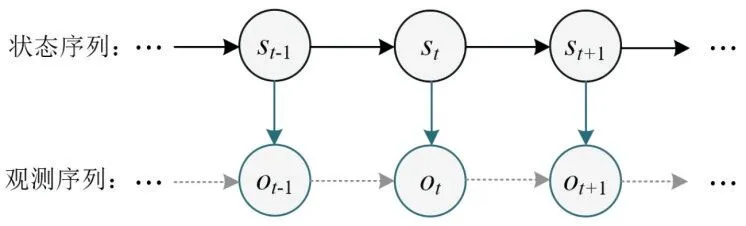
圖1 隱馬爾可夫過程

狀態值與觀測值分別屬于對應的狀態空間與觀測空間。使用Q與V分別表示HMM 的狀態空間與觀測空間：

式中：N與M分別為可能存在的狀態與觀測數量。

隱馬爾可夫模型可以表示為：

式中：A與B分別表示狀態轉移概率矩陣與觀測概率矩陣；π為初始狀態概率向量。

式中：aij為從t時刻狀態為qi轉移到t+1 時刻狀態為qj的概率；bi(k)為t時刻在狀態為qi情況下產生觀測值vk的概率；πi為初始處在狀態qi的概率。

1.2 多觀測非齊次隱馬爾可夫模型

傳統的隱馬爾可夫模型有兩個基本假設：

(1)齊次馬爾可夫性質。對于狀態序列而言，任意時刻狀態只與前一個狀態有關，與其他時刻的狀態和觀察無關。

(2)觀測獨立假設。對于觀測序列而言，任意時刻觀察只取決于同一時刻狀態值，而與其他時刻觀察與狀態無關。

如圖2 所示，本文將傳統HMM 擴展為擁有σ 階記憶馬爾可夫鏈的非齊次HMM，即未來狀態的條件概率分布取決于過去的σ個狀態，同時引入多觀察序列，記為σ-MOHMM。

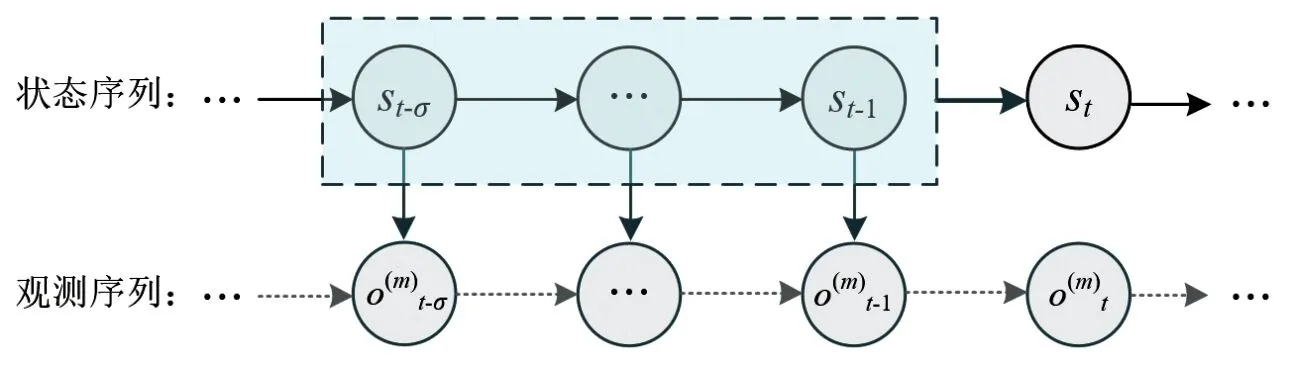
圖2 σ階多觀測隱馬爾可夫模型(σ-MOHMM)

1.3 模型求解

本文采用最大似然估計(maximum likelihood estimate,MLE)、前向后向算法及近似算法來解決光伏概率預測模型建立過程中的學習問題與預測問題。對于HMM，使用MLE 方法得到其轉移概率與觀測概率，可以表示為：

式中：nij為數據集中由狀態qi向狀態qj轉移的個數；nik為在狀態qi下觀測為vk的個數。

對于有N個狀態M個觀測的HMM，狀態轉移概率組成N×N矩陣，觀測概率組成N×M矩陣，矩陣的每一行元素的總和為1，如圖3 所示。

圖3 概率矩陣

σ-MOHMM 的轉移概率與觀測概率矩陣：

高階HMM 概率矩陣的維度隨之增加，圖4 展示了二階狀態轉移概率矩陣，為N×N×N的矩陣。

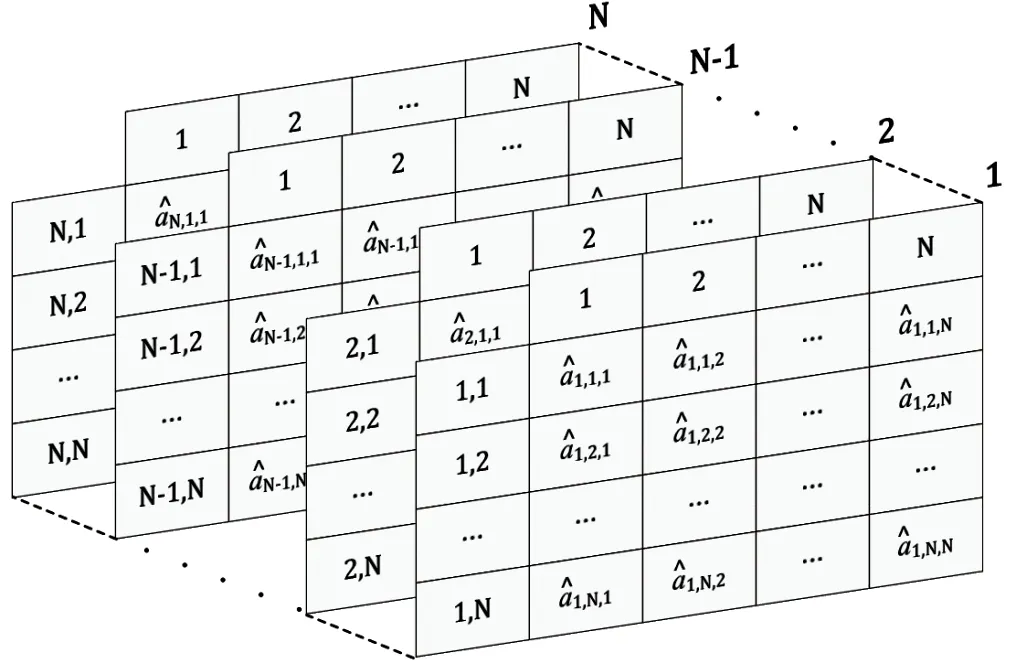
圖4 二階狀態轉移概率矩陣

預測問題是指在給定模型λ 及一定時間段的觀測序列O(d)，計算最有可能出現的狀態序列。對于σ-MOHMM，其前向后向概率可以由以下步驟計算：

(1)計算初值：

式中：α與β分別表示前向概率與后向概率。

(2)迭代計算：

(3)最終，t時刻處于狀態qj的概率可以表示為：

1.4 光伏概率預測模型構建

光伏電站的額定功率決定了其最大出力的理論值。用Pn表示光伏電站額定功率，則狀態空間區間可以表示為[0,Pn]。同理，用Rn表示理論最大觀測值，則觀測空間區間可以表示為[0,Rn]。參數離散化后得到的狀態空間與觀測空間的可以表示為：

式中：θ為百分比參數，θ×Pn與θ×Rn分別為狀態空間與觀測空間的數據間隔。

2 模型輸出與評價指標

2.1 模型輸出

本文采用以下兩種方式計算確定性預測結果：

(1)均值

(2)眾數

置信度1－μ下預測區間可以表示為：

2.2 模型評價指標

采用歸一化均方根誤差(NRMSE)作為確定性預測評價指標，計算方式如下：

式中：T為觀測序列長度，即待預測點個數；st為t時刻實測狀態值；為t時刻預測狀態值；Pn為光伏電站額定出力。

概率預測區間一般從可靠性、銳度兩個方面進行評價。可靠性指標用來描述預測分布與預測對象實際分布的接近程度。采用預測區間覆蓋率PICP來描述預測區間的可靠性，PICP越接近實際置信度(1－μ)%則代表預測結果有更好的可靠性，計算方式如下：

銳度指標用于衡量概率預測結果集中于實際值的程度。采用Winkler 分數(SW)描述模型銳度性能，SW越小則預測結果有更好的銳度性能與綜合性能，計算方式如下：

3 實例分析

本文基于國內某光伏電站時間跨度為2 年的光伏出力及氣象參數數據，電站額定出力20 MW，最大短波輻射810 W/m2，最小潛熱通量－450 W/m2，數據步長為15 min，有效數據698 d。表1 展示了光伏出力與各氣象參數皮爾遜相關性系數關系，選取與光伏出力具有較強相關性的總輻照度與潛熱通量作為觀測變量。由此得到狀態空間與兩個觀測空間區間分別為狀態空間A=[0,20]，觀測空間B1=[0,810]與B2=[－420,0]，離散參數θ為1%。

表1 光伏出力與氣象參數皮爾遜相關性系數表

3.1 模型參數估計

圖5 展示了傳統HMM 模型的狀態轉移概率矩陣直方圖。可以看出，轉移概率分布在矩陣的對角線上，同時由兩側對角線向內逐漸衰減，表明出力數據步長滿足連續時間物理過程的近似表示。圖6 展示了觀測概率矩陣直方圖，相較于狀態轉移概率矩陣更為分散。這意味著同一氣象參數值對應多個光伏出力，從側面印證了光伏發電是一個受到多因素共同作用的復雜隨機過程。

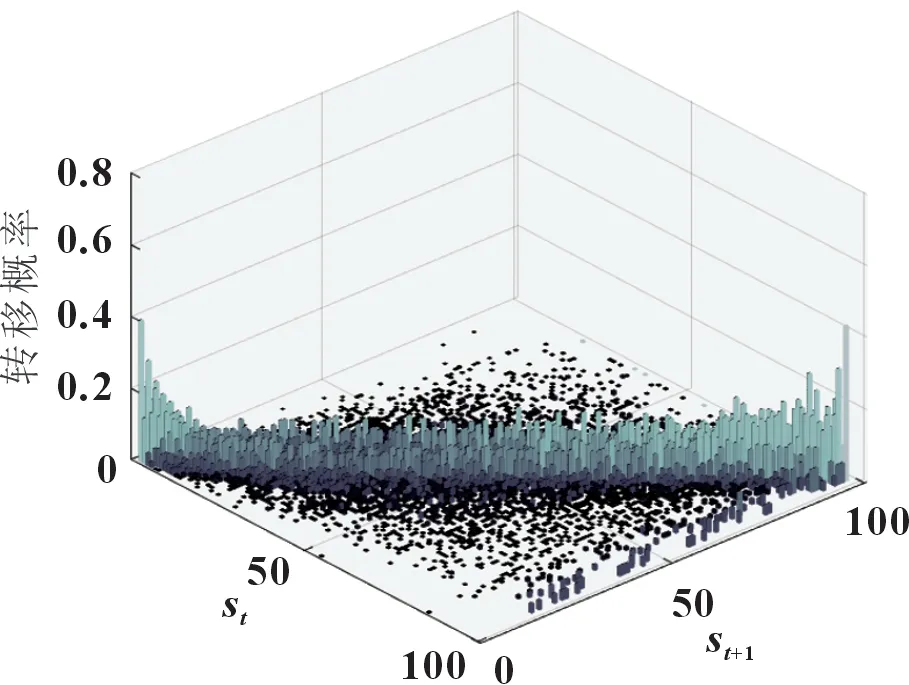
圖5 狀態轉移概率矩陣圖

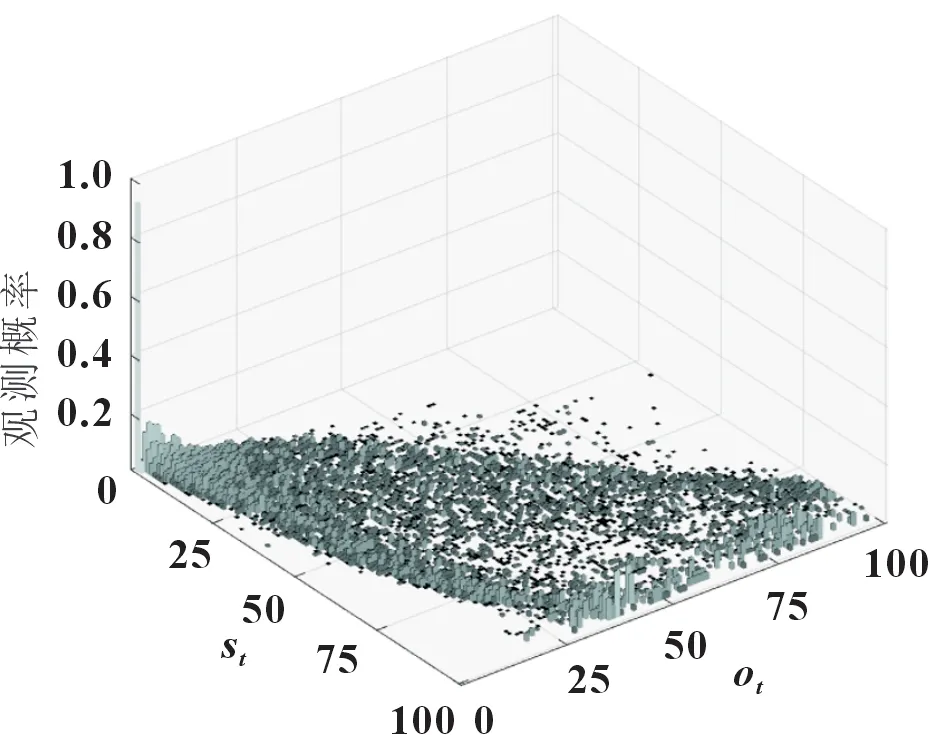
圖6 觀測概率矩陣圖

3.2 預測結果輸出

基于待預測時間段的氣象預測序列，通過計算前向后向算法得到各時刻點對應出力概率分布。如圖7 所示，結果概率分布是一個T×N矩陣，即每個時刻下對應N個狀態的概率分布。基于此，可以得到各時刻點確定性預測結果及不同置信度下預測區間，如圖8 所示。

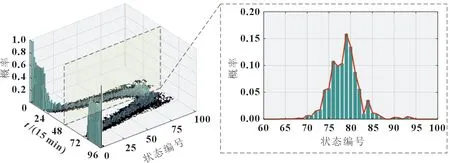
圖7 預測結果概率分布圖

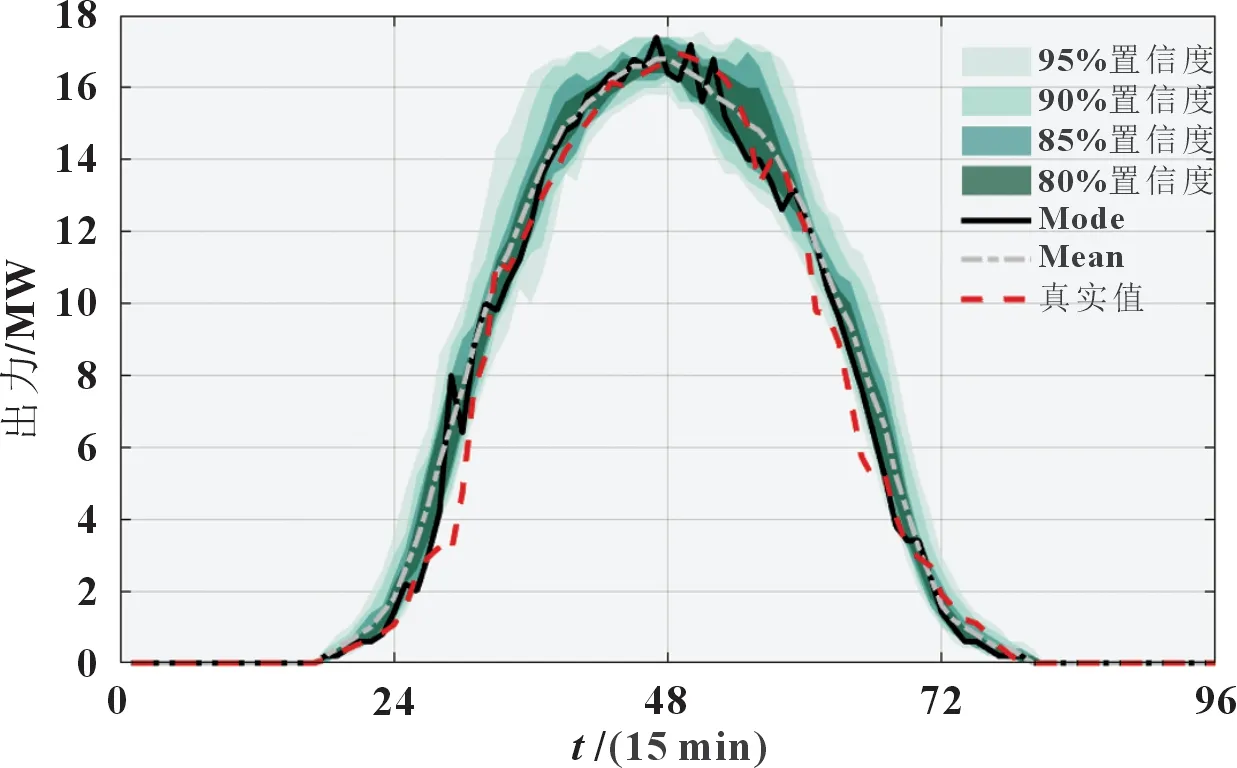
圖8 光伏出力概率預測與確定性預測結果

3.3 模型分析評價

本節將對傳統HMM、2-HMM 以及2-MOHMM 三個概率預測模型的概率預測性能，以及與SVM 模型確定性預測性能進行對比分析。其中，SVM 模型選取徑向基核函數，正則化參數為200，核參數為10。按照以下步驟對上述各個模型進行交叉實驗：(1)隨機選取三天數據作為測試集，其余數據用于模型訓練。(2)訓練好的模型輸出90%置信度預測區間與確定性預測，同時記錄保存模型評價指標計算結果。(3)重復(1)(2)步驟，直至達到設定閾值。(4)對指標進行統計分析，得到預測性能指標分布。

通過測試發現，當閾值達到1 000 次之后，各模型預測性能指標分布趨于穩定，因此選擇測試迭代次數1 000。圖9 與圖10 分別展示了概率預測性能統計結果與確定性預測性能統計結果，以概率密度直方圖形式進行展示，陰影部分為概率分布的核密度估計。

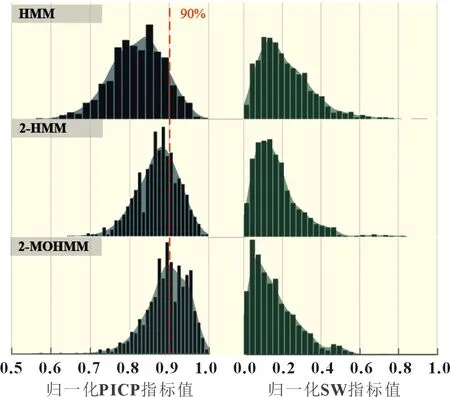
圖9 光伏出力概率預測性能指標統計圖

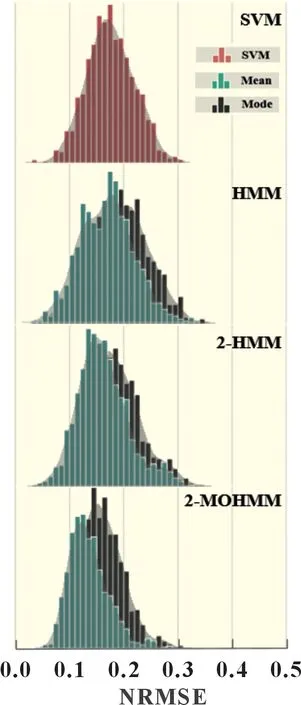
圖10 光伏出力確定性預測性能指標統計圖

由圖9 可以看出，概率預測性能隨著馬爾可夫鏈階數的提升有明顯的提高，具體表現為可靠性指標PICP 分布明顯右移，更接近實際置信度，擁有更好可靠性。同時，區間分數SW隨著階數δ的提升逐漸減小，說明概率預測模型銳度及綜合性能的提升。另一方面，多觀測變量的引入對概率預測模型的可靠性與銳度性能有促進作用。

對于確定性預測結果的輸出而言，均值法相較于眾數法擁有更準確的點預測輸出，指標分布偏向于更小的NRMSE。與概率預測性能類似，階數的提升及雙觀測變量對模型的確定性預測性能有明顯提升。傳統HMM 模型確定性預測性能與SVM 模型接近，擴展后的2-HMM 與2-MOHMM 均明顯優于SVM。

4 結論

本文將隱馬爾可夫模型擴展并應用于短期光伏發電功率預測，包括不同置信水平的概率預測區間及通過統計方法得到確定性預測結果。首先通過確定相關參數邊界及對其離散化處理獲得狀態空間和觀測空間，接著基于真實運行數據建立HMM 概率預測模型，輸出未來時刻點光伏功率概率分布信息。基于真實光伏電站兩年共計698 d 運行數據對傳統HMM、單觀測二階HMM、雙觀測二階HMM 以及支持向量機SVM 四種模型進行了交叉模擬預測實驗。通過統計分析比較各個模型預測性能指標證實了基于HMM 的光伏概率預測模型的可行性與有效性。同時，考慮歷史狀態和觀測對當前觀測和狀態的影響對HMM 模型確定性預測及區間預測性能都有明顯提升。