基于蜜蜂進化型遺傳算法在軌模塊更換的衛星艙布局優化設計

蘇建姜　蘇亮　于波

摘 要：為了解決衛星艙布局優化問題，提出一種加入啟發式規則的蜜蜂進化型遺傳算法（BEGA），進而改善在采用遺傳算法求解衛星艙布局優化時的性能。BEGA算法對交叉操作的改進可以增強種群最優個體所包含信息的開采能力，隨機個體的加入又能提高算法的勘探能力，從而避免算法過早地收斂。同時為了實現在軌模塊更換，通過計算更換模塊和待布物之間干涉量，來求出在軌可更換模塊的合理拆裝路徑，此方法可以有效滿足模塊更換的各項性能指標。最終實現在軌可更換模塊的衛星艙布局優化。仿真試驗表明：BEGA算法可以有效求出安裝路徑，而且與標準遺傳算法（SGA）相比較，BEGA具有較好的包絡圓半徑、轉動慣量、成功率。

關鍵詞：啟發式；蜜蜂進化型；遺傳算法；在軌模塊更換；布局優化；拆裝路徑

Optimization Design of Satellite Cabin Layout for On-Orbit Module Replacement Based on Bee Evolutionary Genetic Algorithm

Su Jianjiang Su Liang Yu Bo

Abstract：In order to solve the problem of satellite cabin layout optimization，a Bee Evolutionary Genetic Algorithm （BEGA） incorporating heuristic rules is proposed to improve performance when solving satellite cabin layout optimization using genetic algorithms.The improvement of BEGA algorithm for crossover operations can enhance the capability of exploiting information contained in the best individuals of the population，and the addition of random individuals can enhance the exploration ability of the algorithm，thus avoiding premature convergence of the algorithm.Meanwhile，in order to achieve on-orbit module replacement，the reasonable disassembly and assembly path of the on-orbit replaceable module is calculated by calculating the interference between the replacement module and the objects to be placed.This method can effectively meet the various performance indicators of module replacement.Finally，the optimization of the satellite cabin layout for on-orbit replaceable modules is achieved.Simulation experiments show that the BEGA algorithm can effectively find the installation path，and compared with the Standard Genetic Algorithm （SGA），BEGA has better envelope radius，moment of inertia，and success rate.

Key words：Heuristic;Bee Evolutionary Type;Genetic Algorithm;On-Orbit Module Replacement;Layout Optimization;Disassembly and Assembly Path

1 引言

隨著人類對空間的探索越來越深入，各種任務對航天器的性能要求越來越高。航天器的結構、組成也日趨復雜，北斗衛星導航系統是我國自主建設、獨立運行的衛星導航系統，是為全球用戶提供全天候、全天時、高精度的定位、導航和授時服務的國家重要空間基礎設施。為了進一步增強航天器的性能、延長航天器使用壽命、降低航天器研制和維護成本、減少人工操作風險，航天器在軌服務技術得到了世界各國的日益重視。目前在航天器在軌維護與服務領域可進行一個或多個在軌可更換航天器在軌維護與服務研究項目，已有成功的范例。［1-3］

在軌服務技術采用在軌燃料加注、模塊更換、在軌組裝等形式對衛星進行空間在軌操作。而作為在軌服務關鍵技術之一的航天器在軌模塊更換，實現衛星性能的恢復、擴展或升級，能夠增強有效載荷的性能、延長衛星使用壽命、降低衛星使用成本，能夠增強衛星任務適應性和操作準備能力。衛星在軌模塊更換技術的發展為提高衛星的可靠性、安全性、經濟性，減少維護成本以及防止災難性事故的發生提供了一條有效的技術途徑。因此，無論是在軍用還是民用方面的應用，在軌模塊更換技術研究對于當前空間技術都具有重大意義。［4，5］

衛星艙有效荷載的布局設計是航天設計中需要解決的問題，且屬于NP難的組合優化問題。求解衛星艙布局優化問題主要有以下幾種方法：遺傳算法、蟻群算法、粒子群算法、人機結合算法、雙系統協同進化法等。［6-9］遺傳算法GA（genetic algorithm）［10］被廣泛地應用于各個領域，［11，12］在衛星艙布局優化方面亦取得了成功的案例。［6］但是在解決衛星艙布局優化問題上傳統遺傳算法同樣存在著早熟收斂和收斂速度慢等問題。［13］本文在總結前人研究結果的基礎上，根據文獻［14］所提蜜蜂進化性遺傳算法，既能提高算法的勘探能力，又可避免算法過早收斂。針對在軌可更換模塊，加入啟發式規則，提出通過計算干涉量的方法求出路徑。這也是本文區別于其他改進算法的主要方面，最終形成具有啟發式規則的蜜蜂進化性遺傳算法在軌可更換模塊的衛星艙布局優化，并將BEGA與標準遺傳算法（SGA）進行比對。

2 蜂群進化型遺傳算法的衛星艙布局優化

2.1 算法原理

蜜蜂進化型遺傳算法［14］（BEGA）就是最近對遺傳算法提出的一種改進，在該算法中由于蜂王的存在，種群的信息開采能力大大提高，因而可以顯著地提高算法的收斂速度，又引入了隨機種群，提高了算法的勘探能力，使算法避免陷入局部最優的困境。在遺傳算法中引入蜜蜂的繁殖進化機制，是為了吸取蜜蜂進化機制的優點，優化遺傳算法的進化結構，促進遺傳算法收斂性能的提高。因此，我們在建立模型結構時有必要對該機制進行簡化。種群的構成：由于工蜂不對進化繁殖過程產生實質的作用，所以種群中我們僅保留雄蜂和蜂王。雄蜂的構成：這一部分的雄蜂主要是從上一代種群中選擇若干雄蜂，參加進化的遺傳操作。外來蜂群的構成：采用隨機產生若干個雄蜂的方法實現。參加交配的蜂群構成：蜂王和被選擇出來的雄蜂以及隨機產生的雄蜂進行交配。

由此，可以得到蜜蜂進化型遺傳算法的代進化模型，如圖 1所示。

為了對BEGA的整個過程進行描述，在上述提出的進化策略基礎之上通過對整個進化過程的分析，設置相應的參數和變量。具體步驟參考文獻。［14］

2.2 啟發式規則

為求解帶平衡約束的矩形布局問題，季美等［15］在BL（Bottom-Left）算法［16］和 BLF（Bottom-Left-Fill）算法［17］基礎上，提出分區域分步布局。由于布局位置是直接計算的，其速度和精度都非常好，但由于其布局條件的限制，要求布局時均為矩形，故在本文圓形布局中有很大的限制。針對本文在軌模塊更換的衛星艙布局優化，為了提高算法計算速度并且滿足優化目標，并且結合分區域分布布局的優點，提出在規定區域布局的啟發式規則。將圓形衛星艙表示為以原點O為中心，以半徑為R的圓，其中R為最大允許的半徑；以縱坐標軸Y將圓分成2個部分，分別記為：Ⅰ、Ⅱ，且衛星艙艙門在右半部分，如圖 2所示，圖中藍色為區域為極角變化范圍，紅色圓弧表示衛星艙艙門。拆裝路徑滿足可達性，即在滿足衛星艙性能指標的前提下，更換模塊盡可能靠近艙門。因此，待更換模塊變化范圍確定在右半平面，即其極角的范圍是［π/2，-π/2］。

2.3 求取拆裝路徑

航天領域研究者早已認識到衛星組件在軌可更換的重要性，并將這些更換的組件和設備定義為ORU（On-orbit Replacement Unit），也提出了ORU模塊設計技術。設計ORU單元的主要目的是為了使得在軌更換操作可有效、便捷和經濟地完成。在軌更換主要是滿足在軌模塊更換的可達性指標。其用來衡量在軌更換模塊接近更換模塊部位的難易程度，可達性指標必然涉及衛星組件的空間位置關系，如被更換組件在空間位置上應盡量不被其它組件遮擋，更換操作時應留有合適的操作空間等。而本文可達性具體實現就是求出更換模塊的可更換路徑。

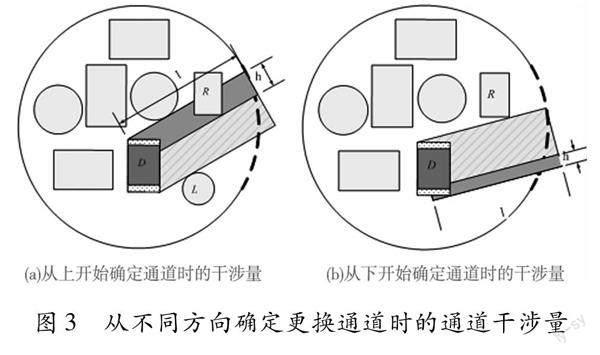
更換路徑的求取實質上是：滿足性能指標的前提下，更換模塊更換時與衛星艙艙體、其它模塊之間不干涉。因此通過計算更換模塊和待布物之間的干涉量來求取更換路徑。由于更換路徑干涉面積為矩形，可以把更換路徑看作一個矩形待布物，通過計算矩形待布物與其他待布物的干涉面積得到.但由于更換通道的角度是任意的，與其他待布物之間并不形成正交關系，所以這種方式計算比較復雜。本文采的是自上而下和自下而上分別求取干涉量的路徑求解方案，且滿足可達性，即所有待布物與更換通道的干涉面積為零，更換模塊離艙門越近越好。對于同一種布局方案，有不同的更換路徑確定方法，不同的更換通道所對應的通道干涉面積是不同的。在遺傳算法迭代中取干涉量最小的值為在軌模塊更換的衛星艙布局設計的更換通道。可更換路徑干涉面積用式（1）表示，不僅方便計算，而且包含了使待更換模塊離艙門越近的約束條件。如圖3（a）所示為自上而下求取通道。圖中藍色區域為可更換模塊，灰色區域為要計算的干涉量，并確立如下關系式：

w=l·h（1）

其中l為更換模塊到艙門之間的距離；h為障礙物侵入更換路徑的距離。

同理如圖3（b）自下而上的干涉量亦可求出，取兩種方法的干涉量較小值，作為約束條件加入到目標函數中。

2.4 實現算法

如何將通道求確方案和蜜蜂進化性遺傳算法結合起來是解決問題的關鍵。本文提出一種通過計算干涉量的通道求取方法，在遺傳算法原有約束條件中加入通道約束條件并實現。

本文在處理衛星艙布局的數學模型時，為簡單起見首先采用線性加權和法將之轉化為單目標優化問題，其次，對于約束條件的處理，采用乘以懲罰系數的方法將之轉化為無約束優化問題。則整個布局方案的評價，即適應度函數的計算可表示如下：

其中，λi（i=1，2，…，a）為各分目標的歸一化因子；ωi，fi（X）（i=1，2，…，a）分別為各分目標的權重系數和分目標表達式，a為分目標的數目；λj（j=1，2，…，b）為各約束條件的歸一化因子；ωj，gj（X）（j=1，2，…，b）分別為各約束條件的懲罰系數和約束條件表達式，b為約束條件的數目。

在蜜蜂進化型遺傳算法之前先加入啟發式規則，并將更換路徑作為約束條件加入到算法適應度函數中，運行算法。BEGA實現具體流程圖如圖 4所示：

3 仿真實驗與結果對比分析

3.1 算例描述

本文采用某氣象衛星進行實例驗證，簡化后的衛星艙模型其艙體是由殼體圍成的回轉圓柱狀空腔。艙體內設有一個大小相同且厚度均勻的垂直于艙的中心軸線（z軸）的圓形承載隔板。艙體分為上部和下部兩個部分，分別用P1和P2表示。本文選定一個待布物視為更換模塊。

該實例的初始數據為：已知承載隔板半徑R=1000mm，兩個布局空間的高度分別為H1=850mm，H2=390mm，承載隔板的厚度D1=D2=20mm。艙體壁及艙內固定件的總質量為379.45kg，其相對參考坐標系Oxyz的質心坐標為C（45，1，943）mm，空艙（裝待布物之前）慣性矩陣I0為：

整星質心的期望值為（0，0，634）mm，實際質心與期望質心的誤差與航天器半徑的比值應小于3%。動平衡度（慣性夾角）誤差許用值δθx′=δθy′=δθz′=0.03rad。本文采用罰函數法，對設計目標和約束條件轉化為單目標函數作為評價函數（適應度函數）。艙體內2個承載面上，要布置給定的15個待布物，其中14個為長方體待布物，1個為圓柱體待布物，要求各長方體待布物正交放置（即θi=0或π/2），并且要求布局設計方案在滿足質量特性約束和使整星的轉動慣量指標最優的條件下，使給定模塊滿足模塊更換的要求。衛星所搭載有效載荷如表 1所示。

3.2 實驗設置與優化目標

本文采用標準遺傳算法SGA，啟發式蜜蜂進化型遺傳算法BEGA對包含15個待布物的衛星艙布局問題就行40次隨機試算。通過SGA和BEGA的比較，檢驗兩種算法在求解復雜在軌更換模塊布局優化的作用和效果。SGA和BEGA每個子種群的規模為40，最大迭代次數為10000。本文設定第8個待布物為更換模塊。

在常規的衛星艙布局設計問題中，需滿足的基本技術指標一般包括：

（1）整個衛星系統的轉動慣量應不大于許用值且應盡可能小；

（2）各待布物之間不得發生干涉；

（3）待布物的任何部分不得超出給定的布局空間，待布物之間預留間隙；

（4）整個衛星系統的靜穩定性（質心距）誤差滿足給定的工程指標要求；

（5）整個衛星系統的平衡度（慣性夾角）誤差滿足給定的工程指標要求等。

本實驗在滿足衛星艙布局優化性能指標的前提下，更換模塊和其它待布物以及艙體的不干涉，即干涉量為零，且靠近衛星艙艙門，此時視為實驗成功。

3.3 實驗結果

本節將分別給出SGA和BEGA在求解上述布局問題時所找到的最優布局方案（包括最優布局方案數值解、最優布局方案圖以及最優布局性能參數列表等），具體內容如下所示：

（1）最優布局方案

每種算法在各自40次計算過程中所得到的最優布局方案數值解如表2所示。

與上述最優布局方案數值解相對應，SGA和BEGA算法所得到的最優布局性能指標如表3。

Rs包絡圓半徑；△S干涉面積；△Sp更換路徑干涉量；T計算時間

與上述最優布局性能指標相對應，SGA和BEGA算法所得到的最優布局方案如圖5，6所示，右側［-π/6，π/6］所標記為更換模塊和衛星艙艙門。

（2）數據統計

本文采用標準遺傳算法SGA、BEGA對算例進行了40次計算，下面給出算法在求解布局問題時的計算統計數據，如表4所示。其中成功率是指每種算法在各自的40次求解計算中滿足在軌模塊更換布局問題設計目標和約束條件的試驗次數與總試驗次數的比值：各數據表中括號內的三組數據依次表示平均值、最小值和最大值。

3.4 性能分析對比

根據上述實驗數據和結果，本節對更換路徑的有效性和標準遺傳算法SGA、BEGA的求解性能進行對比分析，詳情如下：

（1）更換路徑的有效性

由表 3可知，最優布局方案符合衛星艙布局優化設計的性能指標，存在更換模塊與衛星艙艙體和其它待布物之間干涉量為零更換通道，且滿足待更換模塊盡可能靠近艙門的要求，即可達性。

（2）SGA和BEGA的對比分析

在此算例基礎上，本文從如下幾個方面進行對比分析SGA和BEGA的優劣：（a）設計目標（包絡圓半徑）。由表 3，表 4數據可知BEGA所得平均包絡圓半徑較SGA減少0.17965%；（b）轉動慣量。由表 3，表 4可知BEGA所得平均轉動慣量之和較SGA亦減少了1.00578%；（c）計算成功率。BEGA的成功率較SGA提高了20個百分點；（d）計算時間。在計算時間上SGA算法較BEGA減少了13.333%。但從整體看來，BEGA算法的求解質量要優于SGA。

綜上所述，通過計算更換模塊和待布物以及艙體之間的干涉量可以有效求出更換路徑。BEGA在求解在軌可更換模塊的衛星艙布局優化問題時，可有效減少包絡圓半徑，且算法求解成功率明顯提高，轉動慣量之和的平均值減少，提高在軌可更換模塊的衛星艙布局優化設計求解質量。

4 結論

本文針對在軌模塊的衛星艙布局優化，提出通過計算干涉量的方法來確定可更換路徑。為減少計算量在算法中加入啟發式規則，并在蜜蜂進化型遺傳算法中實現。對一個簡化的衛星艙布局設計實例進行數值仿真實驗，證明了SGA和BEGA在求解在軌可更換模塊的衛星艙布局優化問題上的有效性，并且在包絡圓、轉動慣量、成功率上BEGA都優于SGA。

參考文獻：

［1］M.Oda.ETS-VII：achievements，troubles，and future［C］.Proceedings of the 6th International Symposium on Artificial Intelligence and Robotics & Automation in Space：I-SAIRAS 2001，2001：

［2］J.Shoemaker，M.Wright.Orbital express space operations architecture program［C］.Proceedings of SPIE，2004：57-65.

［3］D.M.Waltz，F.Cepollina.On-orbit servicing of space systems［M］.Krieger Publishing Company，1993.

［4］彭成榮.中國航天器總體設計技術的進展［J］.航天器工程，2002，11（1）：3-17.

［5］吳開林.航天器基本特點與設計要求概述（一）—衛星設計特點及任務［J］.航天標準化，2002，1：42-45.

［6］唐飛，騰弘飛.一種改進的遺傳算法及其在布局優化中的應用［J］.軟件學報，1999，10（10）：1096-1102.

［7］張寶，粒子群算法及其在衛星艙布局中的應用研究［D］：大連理工大學，2007.

［8］霍軍周，李廣強，滕弘飛，et al.人機結合蟻群/遺傳算法及其在衛星艙布局設計中的應用［J］.機械工程學報，2005，41（003）：112-116.

［9］崔鋒哲.雙系統協同進化方法及在航天器艙設備布局研究［D］.大連理工大學，2018.

［10］J.H.Holland.Adaptation in natural and artificial systems，University of Michigan press［J］.Ann Arbor，MI，1975，1（97）：5.

［11］馬立肖，王江晴.遺傳算法在組合優化問題中的應用［J］.計算機工程與科學，2005，27（7）：72-73.

［12］尚飛，遺傳算法在圖像處理中的應用研究［D］：華北電力大學 （北京），2007.

［13］王小平，曹立明.遺傳算法：理論，應用及軟件實現［M］.西安交通大學出版社，2002.

［14］孟偉，韓學東，洪炳镕.蜜蜂進化型遺傳算法［J］.電子學報，2006，34（7）：1294-1300.

［15］季美，肖人彬.基于蟻群算法的帶平衡約束矩形布局問題的啟發式求解［J］.計算機應用，2010，30（11）.

［16］B.S.Baker，E.G.Coffman Jr，R.L.Rivest.Orthogonal packings in two dimensions［J］.SIAM Journal on Computing，1980，9（4）：846-855.

［17］B.Chazelle.The bottomn-left bin-packing heuristic：An efficient implementation［J］.Computers，IEEE Transactions on，1983，100（8）：697-707.

（責任編輯 郭曉勇）

收稿日期：2023-01-08

作者簡介：蘇建姜（1987-），男，河北張家口人，碩士，講師，研究方向為智能算法、計算機網絡。