Residual symmetry,CRE integrability and interaction solutions of two higher-dimensional shallow water wave equations

Xi-Zhong Liu(劉希忠), Jie-Tong Li(李界通), and Jun Yu(俞軍)

Institute of Nonlinear Science,Shaoxing University,Shaoxing 312000,China

Keywords: (3+1)-dimensional shallow water wave equation,residual symmetry,consistent Riccati expansion

1.Introduction

In the past few decades,various methods have been proposed and developed to obtain exact solutions to nonlinear partial differential equations (PDEs).These include the inverse scattering transform,[1]Hirota’s bilinear method,[2]Darboux transformation,[3,4]Painlev′e analysis,[5]the Riemann–Hilbert approach,[6,7]etc.It is well known that symmetry analysis can be used not only for simplifying PDEs but also for obtaining their exact solutions.Thanks to Lie’s first theorem,[8]one can find the finite transformation corresponding to a Lie point symmetry group.There are standard methods to find the Lie point symmetry group; for example, one can use the classical Lie group approach or the nonclassical Lie group approach to obtain Lie point symmetry and similarity solutions of a nonlinear PDE.[9–11]On the other hand, although there is no unified way to obtain the nonlocal symmetries of nonlinear systems,we may obtain them through inverse recursion operators,[12]Lax pairs,[13]B¨acklund transformation,[14]conformal invariance,[15]potential systems,[16]etc.

In recent years,Lou found that,for many integrable systems, a nonlocal symmetry called residual symmetry can be obtained via truncated Painlev′e expansion.[16]It was found that the residual symmetry of a system can be localized into a Lie point symmetry by prolonging the system by introducing new dependent variables.In this way, many nonlinear systems have been studied with residual symmetry and new symmetry reduction solutions have been obtained, such as the nonlinear Schr¨odinger equation,[17]the Kadomtsev–Petviashvili equation,[18]the Ablowitz-Kaup–Newell–Segur system[19]and the Gardner equation.[20]

The auxiliary equation method is a simple but effective way to get special solutions, including traveling solitary wave solutions of nonlinear equations.To obtain more generalized solutions, Lou[21]generalized the Riccati expansion method to the consistent Riccati expansion (CRE) method,through which a new integrable property called the CRE integrable is defined and new interaction solutions between solitons and periodic waves are generated for many nonlinear equations.[22–28]The observation of solitons interacting with periodic background waves has been documented in experimental studies.[29]

In this paper, using residual symmetry and the CRE method, we focus on two (3+1)-dimensional shallow water wave equations as follows:[30]

whereu=u(x,y,z,t) in Eqs.(1) and (2) is the free-surface displacement from the equilibrium level of an inviscid incompressible liquid and both of these equations can be reduced to the potential KdV equation by settingx=y=z.Both Eqs.(1) and (2) can be considered as natural expansions of low-dimensional shallow water wave equations,which have many important applications in physical situations such as fluid flows, marine environments, solid-state physics and plasma physics.In Ref.[31], new soliton-like solutions are obtained for the (2+1)-dimensional generalized shallow water wave equation.New analytic solutions, including periodic solitary wave, cross-kink soliton and doubly periodic breather-type solutions, were obtained for a type of (3+1)-dimensional shallow water wave equation by using an optimal system of Lie symmetry vectors.[32]In Ref.[33],Hirota’s bilinear method was used to determine the multiple-soliton solutions of the (3+1)-dimensional shallow water wave equations(1)and(2),which also testified the complete integrability of the two equations.Despite these abundant findings on the(3+1)-dimensional shallow water wave equations,to our knowledge, interaction solutions between solitons and background periodic waves have not yet been obtained and are hard to obtain using traditional methods.

This paper is organized as follows.In Section 2,residual symmetries are obtained and localized in two new prolonged systems for Eqs.(1) and (2), respectively, and new B¨acklund transformations of these two equations are constructed using Lie’s first theorem.In Section 3, using the standard Lie symmetry method we first get the Lie point symmetry group and then give corresponding symmetry reduction solutions for both of the two shallow water wave equations (1) and (2).In Section 5, using the CRE method, we give new B¨acklund transformations of the shallow water wave equations (1) and(2)from which interaction solutions between solitons and periodic waves are generated.The last section provides a short summary.

2.Residual symmetries and related Ba¨cklund transformations for Eqs.(1)and(2)

For Eqs.(1) and (2), we take truncated the Painlev′e expansion as

is a solution of Eq.(1)(or Eq.(2)).

As we know, any Schwarzian-form equations are invariant under the M¨obious transformation

which means that Schwarzian equations have symmetriesσφ=d1,σφ=d2φand

with arbitrary constantsd1,d2andd3.It can be verified thatu0in Eq.(4)satisfies the linearized equations of Eqs.(1)and(2)so we get a nonlocal symmetry for both of the two equations,which is called residual symmetry.

As nonlocal symmetry cannot be used to construct its finite transformation, for the residual symmetry of Eq.(4) we localize it in a new prolonged system by introducing a new variable

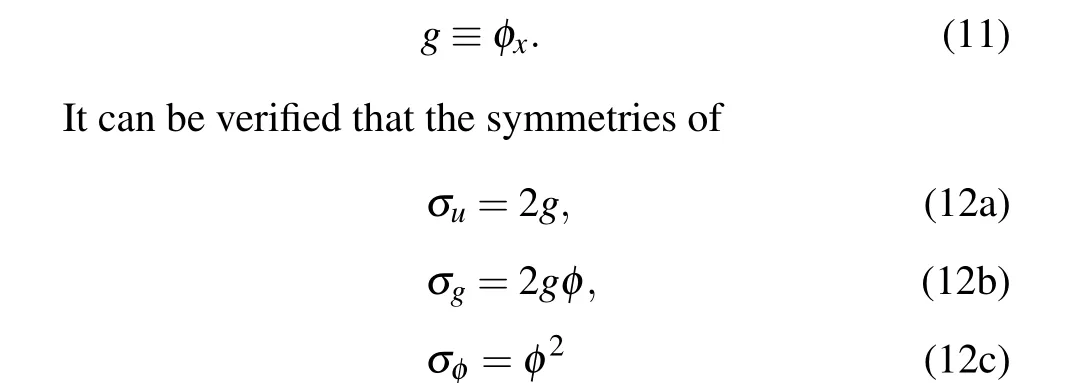
satisfy the linearized system of Eqs.(1),(6),(11)and the linearized system of Eqs.(2),(7)and(11),which means that the residual symmetry can be localized in the two prolonged systems.Equivalently,the symmetry of Eq.(12)can be expressed in a vector form as

we get the following theorem.

Theorem 2If{u,g,φ}is a solution of the prolonged system(1),(6),(11)(or(2),(7)and(11)),then so is{?u,?g, ?φ}with

whereεis an arbitrary group parameter.

3.New symmetry reduction solutions of Eqs.(1)and(2)

For the prolonged shallow water system(1),(6),(11)the Lie point symmetry can be written in vector form as

By substituting Eq.(19) into the linearized equations of the system (1), (6), (11) and vanishing all coefficients of different derivatives of the independent variables ofu,gandφ,we get over-determined linear equations for the infinitesimalsX,Y,Z,T,U,G,Φ, calculated by computer algebra.The final result is

By solving Eq.(28)forΦ,we can get solutions forGandUby Eqs.(26)and(27),and then new solutions of the shallow water equation(1)by Eq.(25).To give a concrete example,by taking a special solution of Eq.(28)as

whereEFis an incomplete elliptic integral of the first kind andc,l1,ω1,l2,ω2,k2,m,nare all arbitrary constants, we get a new solution of Eq.(1)

which can be verified by substituting it into Eq.(1).

For the prolonged system (2), (7), (11), using a similar procedure as in the case of the prolonged system(1),(6),(11),we can get the Lie point symmetry as

wherefi(i=1,2,...,10)are arbitrary functions of indicated variables.When takingf7(y,z)=2,fi=0(i/=7)in Eq.(31),the symmetry degenerates into the special case of Eq.(13).

By settingf1(z) =c1,f2(z) =c2,f3(z) =c3z+c4,f4(z)=c5,f5(z)=c6,f6(z,t)=c7,f7(y,z)=1,f8(z,t)=0,f9(y,z)=c8,f10(y,z)=c9withci(i=1,2,...,9) being arbitrary constants in Eq.(31),we get symmetry reduction solutions of the prolonged system(2),(7),(11)

SolvingΦby Eq.(37), we can obtain new exact solutions of Eq.(2)by using Eqs.(36),(35)and(34).In particular,when solutions of Eq.(37) are taken as periodic functions, the solutions of (34) are interaction solutions between solitons and background periodic waves.

4.CRE integrability and new interaction solutions of Eqs.(1)and(2)

Using the CRE method, the generalized Riccati expansions of Eqs.(1)and(2),which can be determined by balancing the highest nonlinear term and the dispersion term, take the form

From the above discussions we get a B¨acklund transformation for Eqs.(1)and(2),which can be summarized as follows.

Theorem 3Ifwis a solution of Eq.(42)(or(43)),then

is a solution of Eq.(1)(or Eq.(2)),whereR=R(w)is a solution of the Riccati equation(39).

As a special case of the CRE method we consider the application of the consistent tanh expansion (CTE) (whereR(w)=tanh(w)in Eq.(39))on Eqs.(1)and(2).To this end,we take

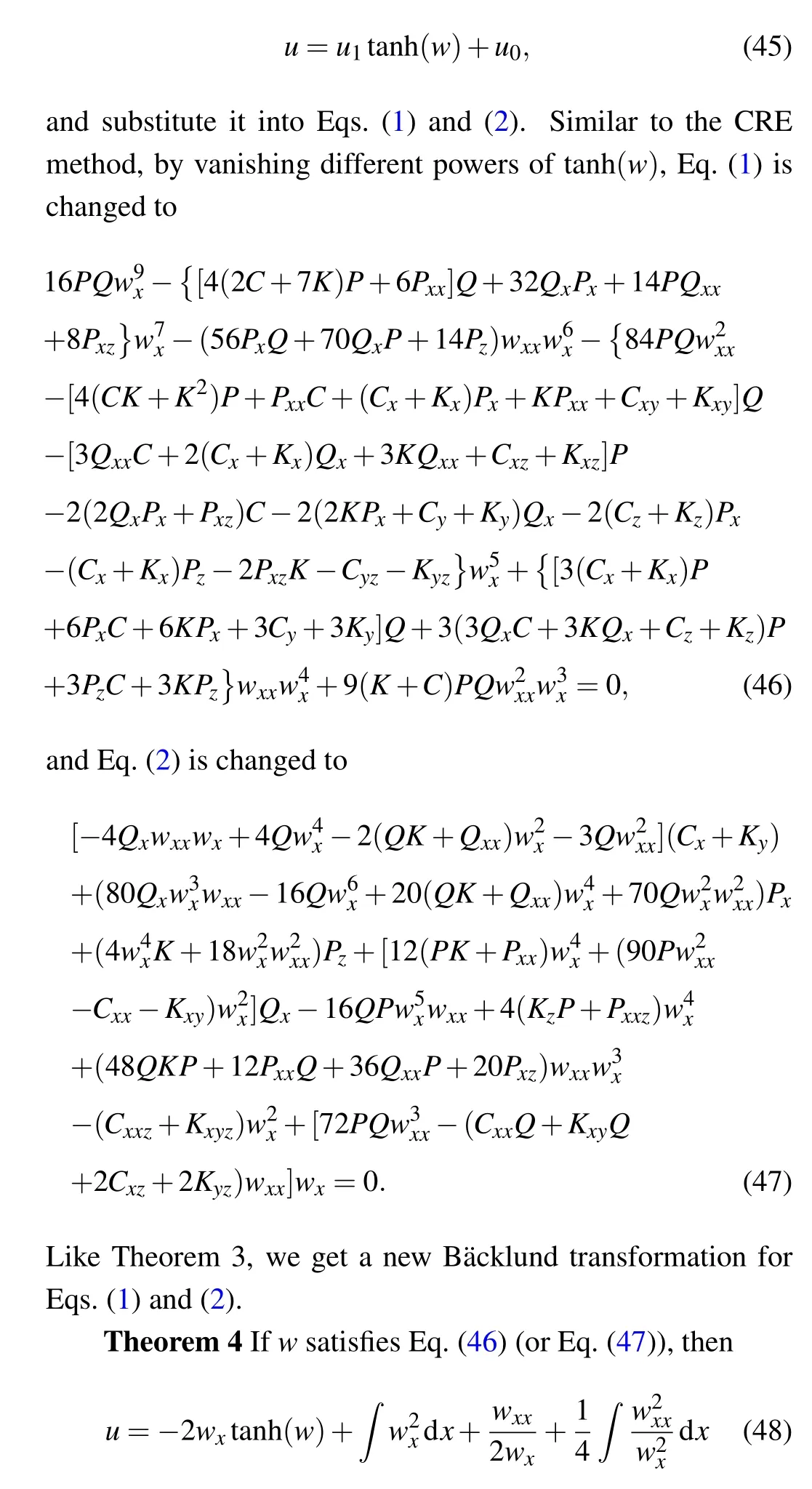
is a new solution of Eq.(1)(or Eq.(2)).

Below,we give some new solutions of the shallow water equations(1)or(2)by using Theorem 4.We assume that the solution of Eq.(46)or(47)has the form of

wherek,l,m,ωare arbitrary constants andgis an arbitrary function ofx,y,zandt.Some nontrivial solutions of the shallow water equation(1)(or Eq.(2))can be generated by trivial solutions of Eq.(46)(or Eq.(47)).

We consider two special cases.

Case 1For Eq.(1),it can be easily checked that

It can be seen from the expressions of Eq.(54)with Eqs.(55)–(58)that the free parameters therein can be chosen as any real number withk1k2/=0 to avoid singularities.Figure 1 gives a picture of the interaction solution of Eq.(54)with Eqs.(55)–(58)by settingy=t=0,the other parameters are fixed by

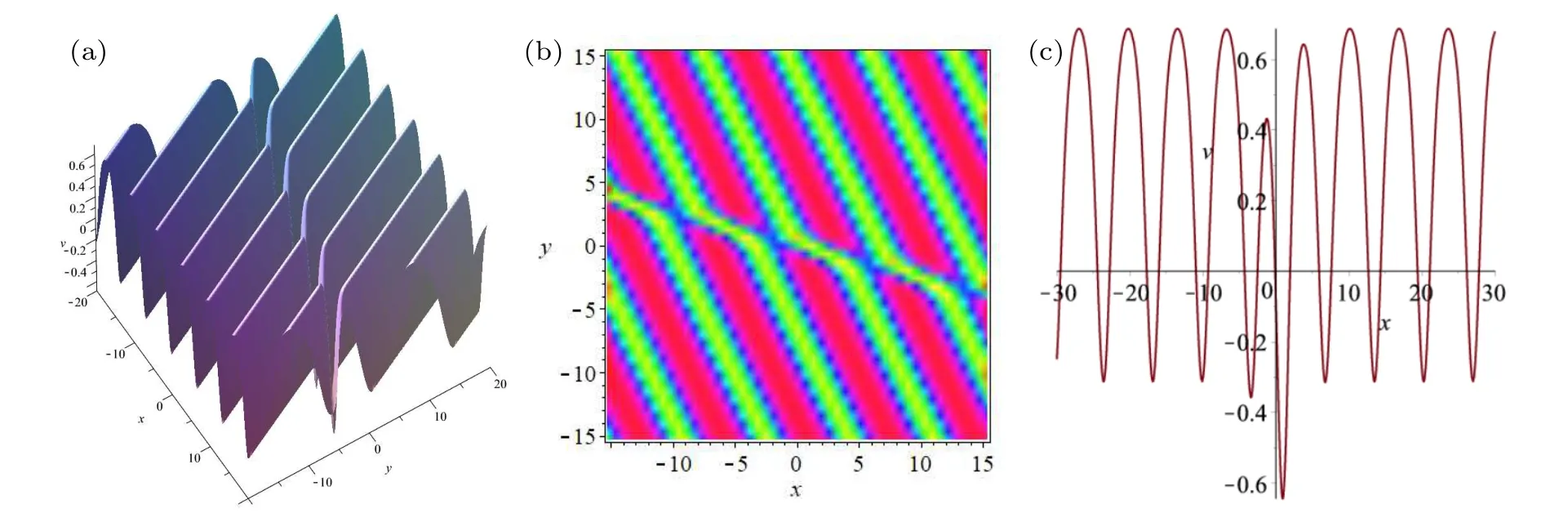
Fig.2.The interaction solution (54) with Eqs.(55), (60), (57) and (61), where the parameters are fixed by Eq.(62) and v=ux: (a) the threedimensional plot with z=t=0;(b)the density plot with z=t=0;(c)the one-dimensional plot with y=z=t=0.

Similarly, it can be seen from expressions of Eq.(54)with Eqs.(60) and (61) that the free parameters therein can be chosen any real number withk1k2l2/=0 to avoid singularities.Figure 2 displays the interaction solution (54) with Eqs.(55), (60), (57) and (61) where the parameters are fixed by

It can be seen from Figs.1 and 2 that the shallow water equations of Eqs.(1)and(2)have similar interaction behaviors between soliton and background periodic waves.but also have different interaction features,which are shown Figs.1(b)and 2(b) as interactions along straight lines with different slopes or,in other words,the positions of interaction between soliton and periodic waves between Eqs.(1)and(2)are different.

5.Conclusion

In summary, two high-order shallow water wave equations are studied by using the standard Lie group method and the CRE method,respectively.After localization of the residual symmetries,new symmetry reduction solutions for the two shallow water wave equations are obtained,from which abundant new exact solutions can be generated.The two high-order shallow water wave equations are proved to be integrable in the sense of having consistent Riccati expansions.Some nonauto B¨acklund transformations for the two high-order shallow water wave equations are derived by using the CRE and CTE methods.Using the non-auto B¨acklund transformation theorems, a new type of interesting interaction solutions between solitons and cnoidal periodic waves is obtained and their detailed interaction behaviors are revealed by their plots and analysis.All the exact solutions in this paper are verified to be correct by substituting them into the (3+1)-dimensional shallow water wave equations(1)and(2).

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.11975156 and 12175148).