水平井鉆井提速-減阻-清屑多目標協同優化方法*

丁建新 李雪松 宋先知 張誠愷 馬寶東 劉子豪 祝兆鵬

(1.昆侖數智科技有限責任公司 2.中國石油大學(北京)油氣資源與工程全國重點實驗室 3.中國石油大學(北京)石油工程學院)

0 引 言

近年來，我國油氣對外依存度持續處于高位，2022年石油和天然氣對外依存度分別達到71.2%和40.5%，遠超國際能源安全預警標準[1]。因此，加大油氣勘探開發力度，保障國家能源安全，是我國油氣行業未來發展的主要任務。鉆井工程是油氣資源勘探開發的關鍵環節，保證安全高效鉆進是實現油氣勘探開發、降本增效的重要保障。其中鉆井過程包含鉆進破巖、管柱延伸和井筒流動等多個復雜過程[2-4]，國內外專家學者在鉆速優化、摩阻計算和井筒流動等多個方面進行了深入研究。

鉆井過程中的機械鉆速是反映鉆井效率的關鍵指標，而準確預測鉆速是破巖提速的基礎。目前鉆速預測主要有統計回歸和智能預測2種方法。國外學者基于室內試驗或者現場數據，通過分析鉆具、工程和地層等各類因素對機械鉆速的影響機理，構建了Maurer、Warren、Bourgoyne-Young、Hareland鉆速方程以及修正的楊格鉆速方程等多種方程。國內學者同樣基于多元回歸方法分析求解鉆速方程，為鉆速預測提供了理論支撐[5]。隨著人工智能技術與傳統油氣行業的深度融合，鉆速智能預測方法逐漸成為行業研究熱點，支持向量機[6]、隨機森林[7]等機器學習方法為鉆井工程參數與鉆速之間映射關系的構建提供了新的方法和思路，而全連接神經網絡(FCNN)[8]、循環神經網絡(RNN)[9]等深度學習模型借助其非線性建模能力和高維特征分析能力，在精度、泛化性提升等方面已取得顯著效果。

管柱摩阻是評價水平井鉆井風險的重要因素，摩阻過大會降低鉆壓、扭矩傳遞效率，影響巖石破碎效果，嚴重時可能導致卡鉆等風險。摩阻扭矩的傳統計算方法主要有軟桿模型[10]和剛桿模型[11]，分別適用于直井和水平井。有限元、有限差分、加權殘值等方法也逐步應用到管柱摩阻扭矩相關研究中，為管柱下入能力評價及卡鉆分析提供理論基礎。近年來，有學者采用回歸分析、隨機森林等機器學習算法[12]對摩阻扭矩進行實時預測，利用改進的BP神經網絡[13]建立摩阻系數與影響因素之間的隱含關系，實現了摩阻系數的高效計算。例如，李紫璇等[14]考慮了巖屑床對管柱摩阻扭矩的附加影響，提高了卡鉆預測精度。

井眼清潔是影響水平井鉆井風險的另一個關鍵因素。鉆井過程中產生的巖屑在重力作用下極易在斜井段、水平段沉積并形成巖屑床，掩埋管柱，導致鉆桿扭矩增大[15]。因此學者們開展了相關試驗，研究環空流速、鉆井液密度和流變性、巖屑粒徑、機械鉆速等參數對巖屑床高度等井眼清潔關鍵參數的影響規律，隨后提出了經典的分層模型和臨界速度模型。例如：馬志忠等[16]探索了井眼清潔計算新方法，提高了環空巖屑濃度和井筒ECO的計算精度；張菲菲等[17]結合傳統水力學模型和人工智能方法，提出了數據驅動定量評價巖屑動態分布的新方法，為解決大位移井井眼清潔不充分提供了詳細井下信息。

綜上，前人針對破巖提速、管柱減阻和井筒清潔3個方面開展了大量研究，為鉆井效率優化和風險管控提供了堅實的理論基礎。但是，鉆井過程中這3個子系統相互耦合、相互制約，優化鉆井過程需要綜合考慮風險和效率，現有單過程、單目標優化方法難以取得全局最優效果[18-19]。例如，提高鉆速會增大巖屑量，巖屑床堆積過高可能會增大鉆柱摩阻造成卡鉆，也會降低鉆壓導致鉆速下降。因此在鉆井多過程優化方面，挪威eDrilling公司集成了水力學、管柱力學、機械鉆速等多個模塊，搭建了鉆井數字孿生系統[20-21]，實現了鉆井全生命周期的動態監測與參數優化。挪威NORCE研究所構建了自動化鉆井系統[22-23]，能夠實現鉆井優化、軌跡調控和風險處理等功能。盡管上述工作考慮了部分鉆井過程子系統的耦合，但在協同鉆速、摩阻和巖屑運移等方面仍然有待深入研究。

為此，本文提出一種考慮破巖提速-管柱減阻-井筒清潔3個子系統協同作用的水平井鉆井多目標優化方法。該方法以提高機械鉆速、降低機械比能為目標，以鉆壓、轉速和排量為調控參數，以減小管柱摩阻、促進井筒清潔為約束條件，通過耦合鉆速預測、摩阻系數反演和巖屑運移模型模擬，實現水平井鉆井提速-減阻-清屑多目標協同優化，為現場安全高效鉆進提供保障。

1 提速-減阻-清屑協同優化方法

1.1 數據處理

本文選擇某油田1口水平井進行實例分析。該井井深7 788 m，造斜點位于井深7 105 m，表1列舉了部分測井和錄井參數。在數據處理方面，通過KNNImputer函數[24]計算各數據的歐幾里德距離，尋找最近鄰樣本，使用最近鄰樣本非空數值的均值來填補缺失值；基于箱線圖法[25]計算中位數和四分位數，獲取數據正常值的上、下邊界，并以此為依據剔除上、下邊界外的異常值。

1.2 機械鉆速智能預測模型

在鉆速智能預測方面，神經網絡、隨機森林和支持向量機是當前研究最充分、使用最廣泛的模型之一[26-27]。其中，隨機森林[28]是一個集成了許多決策樹的智能學習機器，模型示意圖見圖1。

決策樹是相對簡單的決策模型，具有類似流程圖的樹狀結構，每棵樹都由不同節點(根節點、內部節點和葉節點)組成，可將輸入數據分解為更小的子集。作為一個包含許多決策樹的集成學習器，隨機森林通過綜合所有決策樹的預測結果來給出輸出。與神經網絡和支持向量機相比，隨機森林的一個優點是預測結果更穩健，輸出會始終處于訓練標簽的范圍內，不會像神經網絡一樣給出不合理的異常預測結果[29]。此外，C.SOARES等[30]、ZHANG C.K.等[31]分別對比了3種模型在鉆速實時預測與優化方面的準確性和穩定性，認為隨機森林優于神經網絡和支持向量機。故本文采用隨機森林預測機械鉆速。

模型超參數是指在模型訓練開始前應設置的參數。例如，在訓練隨機森林之前，應人工確定樹的數量、每棵樹的最大深度等。人工智能模型的性能在很大程度上依賴于模型的超參數設置，因此，需要在模型開始訓練前進行超參數調優[32]。網格搜索法和隨機搜索法是2種常見的超參數調優方法[33]。其中，網格搜索法遍歷比較模型在所有超參數組合下的性能，其結果最為準確，但計算代價高昂。例如，要為具有m個超參數且每個超參數都具有n個候選值的模型選擇最佳超參數時，模型必須運行mn次。相反，隨機搜索法僅從所有超參數組合中隨機選擇若干進行比較，與網格搜索法相比，在效果相似的情況下可大大縮短訓練時間。因此，本文采用隨機搜索法對隨機森林的超參數進行自動調優。表2列出了模型超參數及其取值范圍[30]。

表2 隨機森林模型超參數及其取值范圍Table 2 Hyperparameters of random forest model

1.3 水平井摩阻系數智能反演模型

管柱摩阻扭矩計算機理模型主要有軟桿模型和剛桿模型，其中剛桿模型相較于軟桿模型考慮了鉆柱剛度，更適合大位移井、水平井的摩阻扭矩計算，因此本文采用剛桿模型進行水平井的摩阻系數反演[34]。

鉆柱整體受力微分方程如下：

(1)

(2)

式中：F為鉆柱上的軸向壓力，N；q為單位長度鉆柱重力，N/m；s為井深，m；“?”代表鉆柱狀態，負號代表提拉，正號代表下入；α為井斜角，rad；EI為鉆柱的抗彎剛度，N·m2；nt為鉆柱與井壁的接觸力，N/m；μ1為鉆柱軸向摩阻系數；μ2為周向摩阻系數；M為鉆柱所受扭矩，N·m；kb為井眼軸線曲率，m-1；Do為鉆柱外徑，m。

井眼曲率kb的計算公式為：

(3)

鉆柱上的接觸力nt計算公式為：

(4)

(5)

(6)

(7)

利用有限差分數值求解方法，可將鉆柱整體受力模型寫成以下形式(以壓力為正)：

(8)

(9)

式中：Fi和Fi+1分別為第i段鉆柱單元靠近地面和靠近井下兩端的軸向力，N；MTi和MTi+1分別為第i段鉆柱單元兩端的扭矩，N·m；Kbi和Kbi+1分別為第i段鉆柱單元兩端的井眼曲率，m-1；qi、EIi、nti、Δsi和Dbi分別為第i段鉆柱單元的線重力(N/m)、抗彎剛度(N·m2)、與井壁的接觸力(N/m)、單元端的長度(m)和外徑(m)。

本文采用二分法進行鉆柱周向摩阻系數的反演，計算流程如圖2所示。根據計算流程，首先在0～1之間選取初始摩阻系數，將其與預測得到的井底鉆壓、扭矩帶入到鉆柱整體受力模型中[35]；利用傳遞方程從鉆頭處向上依次計算每個鉆柱單元的軸向力和扭矩；比較計算得到的地面大鉤載荷、轉盤扭矩與實際測量值的誤差，若誤差在允許范圍內，則說明給定的摩阻系數較為準確，否則利用二分法對摩阻系數重新賦值計算。最終輸出鉆柱整體軸向力、扭矩及彎矩等參數。

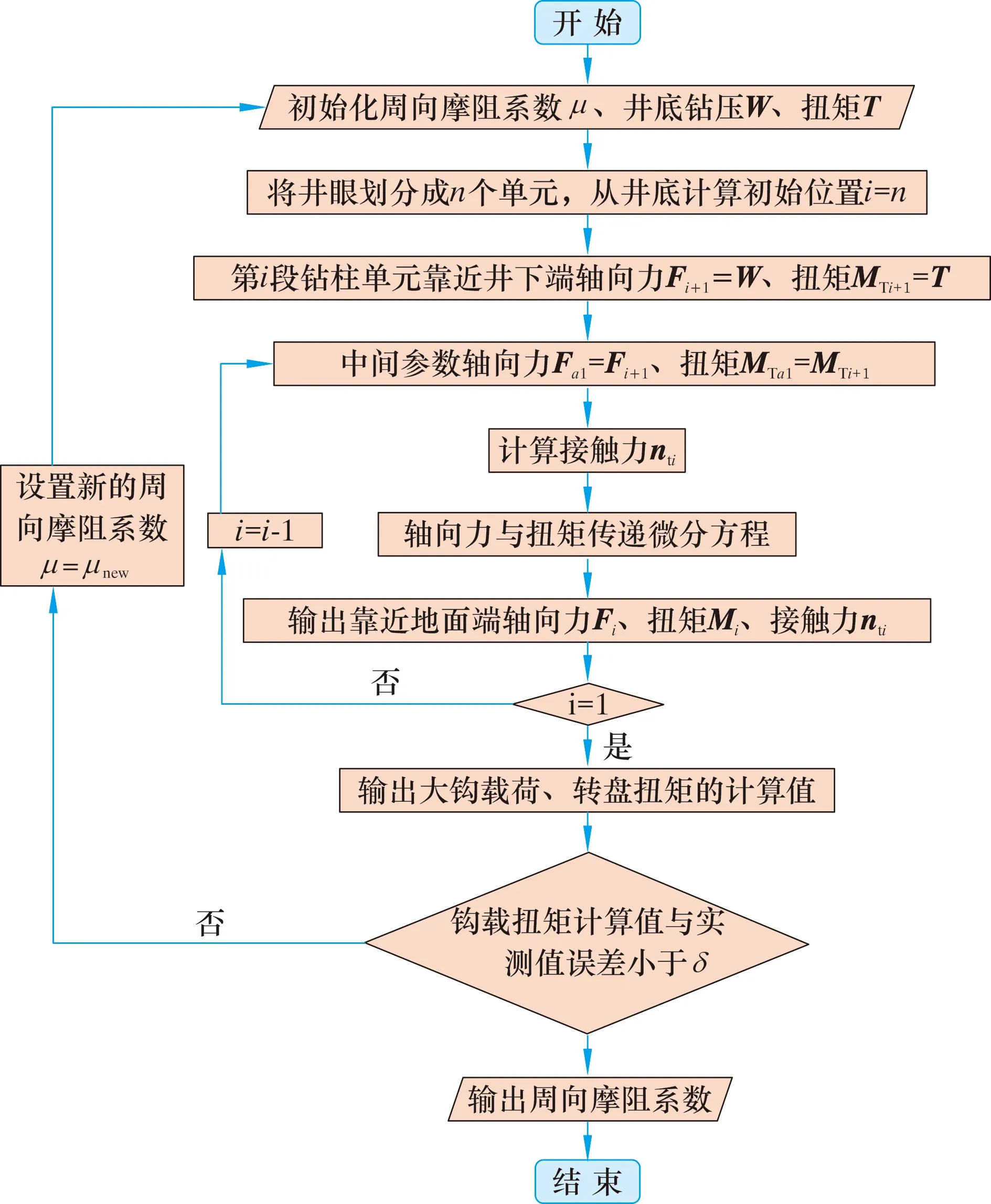
圖2 二分法反演摩阻系數計算流程圖Fig.2 Flowchart for calculating friction coefficient by inversion using dichotomic method

1.4 水平井井眼清潔計算模型

本文采用巖屑運移2層穩態模型進行巖屑床高度的計算。模型將井筒內的巖屑床截面分為懸浮層和移動巖屑床2層運移，如圖3所示。其控制方程包括：巖屑質量守恒方程、液相質量守恒方程、懸浮層動量守恒方程、移動巖屑床動量守恒方程、懸浮層巖屑擴散方程[36]。

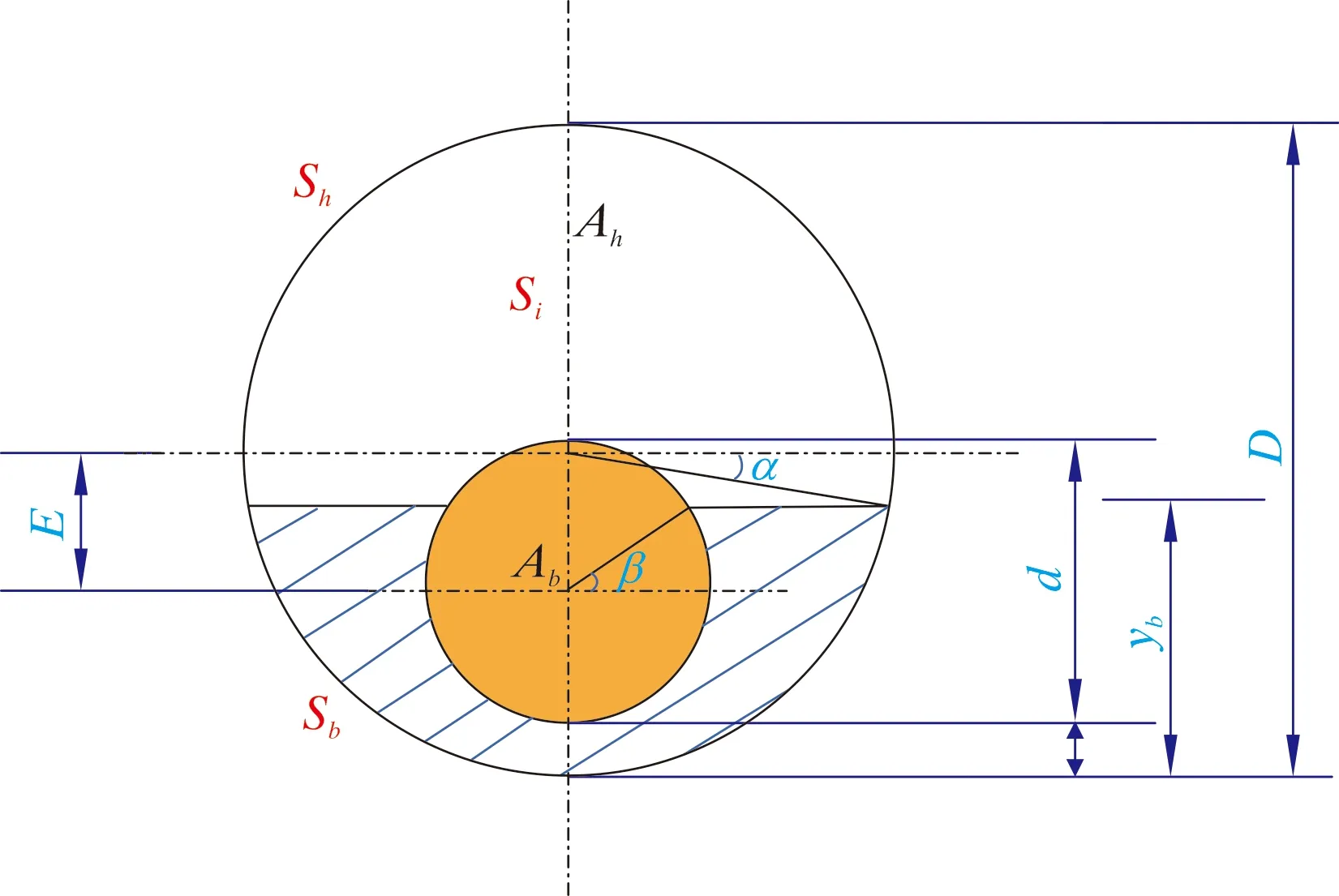
圖3 懸浮層和巖屑移動床2層運移示意圖Fig.3 Schematic diagram of two-layer transport of suspended layer and cuttings bed

巖屑質量守恒方程：

UhChAh+UbCbAb=UsCsA

(10)

液相質量守恒方程：

Uh(1-Ch)Ah+Ub(1-Cb)Ab=Us(1-Cs)A

(11)

懸浮層動量守恒方程：

(12)

移動巖屑床動量守恒方程：

(13)

懸浮層巖屑擴散方程：

(14)

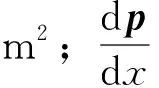
依據巖屑床高度計算環空幾何結構參數，采用迭代法和割線法進行求解，求解流程如圖4所示。

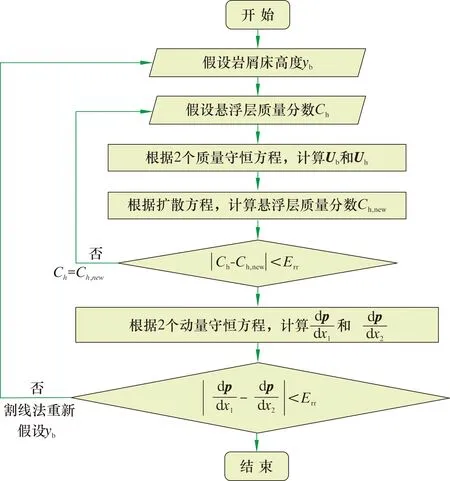
圖4 2層巖屑床運移模型求解流程圖Fig.4 Flowchart for solving of two-layer cuttings bed transport model

首先給定巖屑床高度(yb)和懸浮層質量分數(Ch)的初始值，根據質量守恒方程計算巖屑床速度(Ub)和懸浮層速度(Uh)；根據擴散方程得到懸浮層巖屑質量分數。與初始值對比，若誤差超出允許范圍，則重新賦值懸浮層質量分數，迭代計算；根據2個動量守恒方程，計算單位長度壓降，判斷二者誤差是否在允許范圍內，若不在允許的范圍內，則采用割線法重新假設巖屑床高度進行計算。經反復迭代計算后，最終得到巖屑床高度等參數。

1.5 提速-減阻-清屑多目標協同優化方法

提速降本是油氣鉆井的優先目標，但優化鉆速等鉆井效率指標時還需考慮到潛在的鉆井風險。本文以提高機械鉆速、降低機械比能為目標，以鉆壓、轉速和排量為調控參數，以減小管柱摩阻、促進井筒清潔為約束條件，基于鉆速智能預測模型、摩阻系數智能反演模型和水平井巖屑運移模型，構建了鉆井提速-減阻-清屑多目標協同優化框架，如圖5所示。多目標協同優化具體流程(步驟)如下。

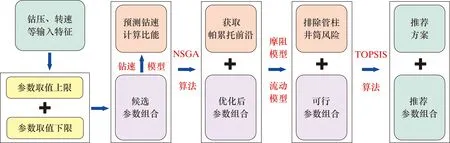
圖5 水平井鉆井提速-減阻-清屑多目標協同優化框架Fig.5 Multi-objective collaborative optimization framework for ROP improvement， drag reduction and hole cleaning in horizontal well drilling

(1)處理數據，訓練鉆速智能預測模型。采用1.1節所述方法處理數據缺失值和異常值，基于1.2節中的隨機森林模型和超參數調優方法訓練、優化機械鉆速智能預測模型。

(2)設定工程參數上、下限，得到候選參數組合。人工智能模型是從給定訓練數據集上學習目標變量與輸入變量的映射關系，所以當訓練好的智能模型應用于非訓練集數據時，其輸入參數一般不能與訓練集參數差別過大，否則將難以取得準確的預測結果。鉆壓、轉速和排量作為司鉆調控鉆井過程的主要變量，若根據鉆井設備上標定的范圍取值，有可能取到不在訓練集內的參數。因此，為保證預測模型的準確性，本文分別從訓練數據集中取鉆壓、轉速和排量的最大值和最小值作為其取值上、下限，在上下限之間隨機取值，得到候選調控參數(鉆壓、轉速和排量)組合。

(3)基于NSGA-Ⅱ算法進行多目標優化。本文以機械鉆速和機械比能作為優化目標，屬于多目標優化問題，文中采用改進非支配排序遺傳算法(Non-dominated sorting genetic algorithm -II，NSGA-Ⅱ)[31，37-40]求解該問題。NSGA-Ⅱ是目前廣泛使用的多目標遺傳算法之一，它降低了非劣排序遺傳算法的復雜性，具有運行速度快、收斂性好的特點。將步驟(2)中候選調控參數組合輸入NSGA-Ⅱ算法中，求解后可獲得帕累托解集以及其對應的參數組合，此解集和參數組合將作為后續進行風險約束和多方案決策的基礎。

(4)基于摩阻系數反演模型和巖屑運移模型施加風險約束。步驟(3)計算帕累托解集時僅考慮了機械鉆速和比能2個目標，其對應的調控參數(鉆壓、轉速和排量)有可能造成管柱屈曲、卡鉆以及井眼清潔等問題。因此，需要排除這些有可能造成鉆井風險的解。將優化后的參數組合輸入摩阻系數反演模型和巖屑運移模型，分別計算該參數組合下的摩阻系數、摩阻力和巖屑床高度，根據摩阻系數判斷是否有卡鉆風險，根據巖屑床高度判斷是否符合井眼清潔條件。本文以周向摩阻系數大于0.5為判斷有卡鉆風險的依據[34]，以巖屑床高度大于井眼直徑10%為判斷不滿足井眼清潔條件的依據[41]。淘汰不滿足風險約束的參數組合后，即得到可行的參數組合。

(5)基于TOPSIS算法進行多方案決策。步驟(4)淘汰了帕累托解集中有可能導致鉆井風險的解，得到了所有可行的參數調控方案。本文采用逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)[31，42]，從多個可行方案中決策給出最佳方案。該算法是一種廣泛使用的綜合評價方案，它能夠充分利用原始數據信息，通過計算各方案與最優方案、最劣方案間的距離來進行評分，并以評分優劣為依據進行排序。基于TOPSIS算法對步驟(4)得到的可行參數集合進行決策，可獲得最優參數組合方案。此方案能夠取得機械鉆速和機械比能的相對最優值，且不會引起屈曲、卡鉆和巖屑床堆積等鉆井風險。

2 應用實例分析

將本文提出的水平井鉆井提速-減阻-清屑多目標協同優化框架應用于該井7 600～7 650 m的水平段，分析其在機械鉆速預測、鉆速-比能協同優化、風險約束等方面的效果。

圖6展示了協同優化方法在訓練集(7 600 m前數據)上的機械鉆速預測效果。該井訓練數據集上的平均機械鉆速為5.6 m/h，與本文提出的機械鉆速智能預測模型平均絕對誤差約為0.2 m/h，平均預測誤差約為3.9%，且95%情況下其絕對和相對預測誤差分別小于0.7 m/h和10%。

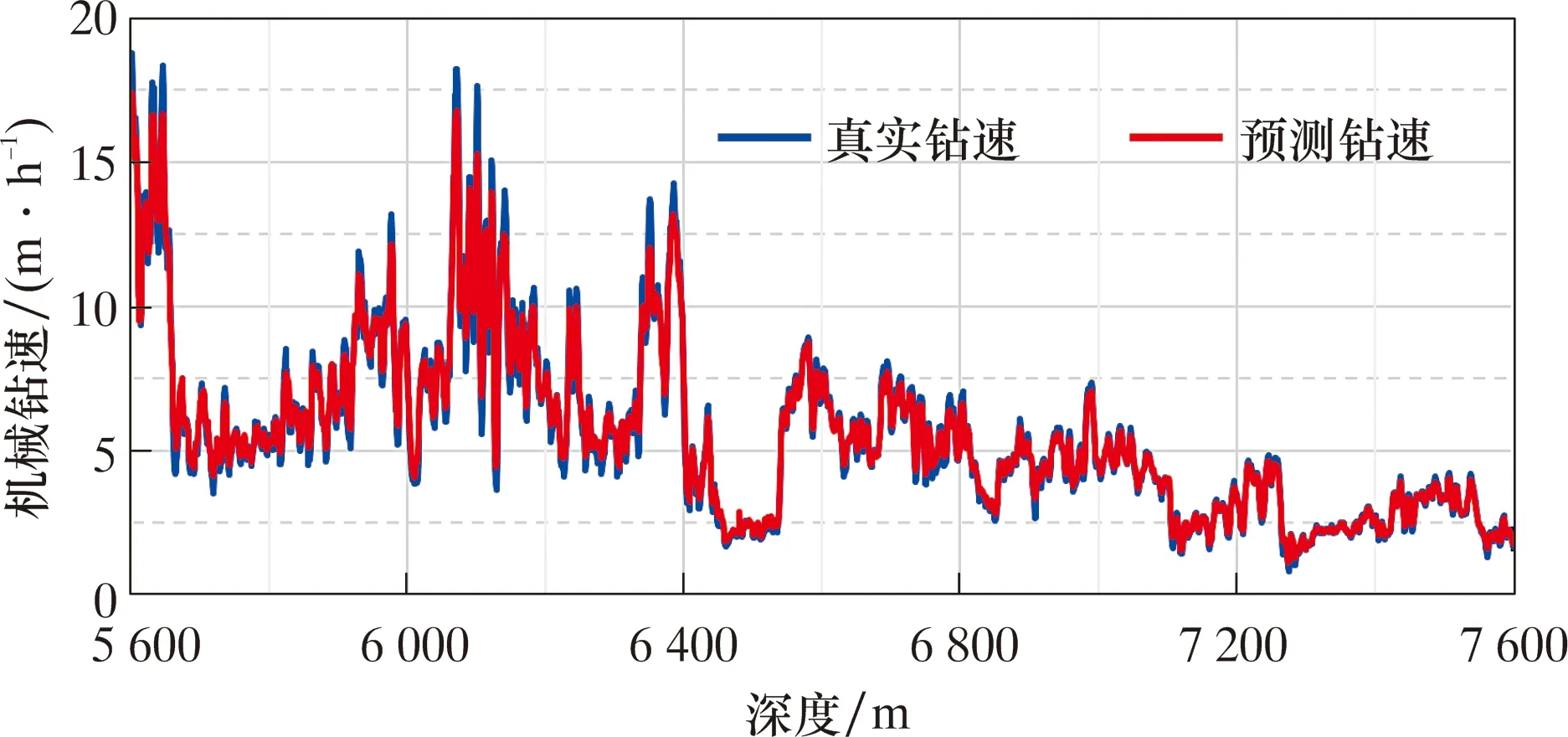
圖6 部分訓練集(7 600 m前數據)機械鉆速預測效果Fig.6 Prediction effect of ROP of some training sets (data before 7 600 m)

圖7對比了7 600～7 650 m的實際機械鉆速、預測機械鉆速和優化后機械鉆速。鉆進7 600～7 650 m時的平均機械鉆速為2.7 m/h，該模型預測的平均機械鉆速為2.5 m/h；其平均絕對預測誤差為0.3 m/h，平均相對預測誤差為11.6%。優化后，平均機械鉆速提高至3.4 m/h，相較優化前提高了32%，且僅在7 638 m、7 639 m和7 640 m處由于鉆速預測模型誤差過大(約15%)而低于優化前。

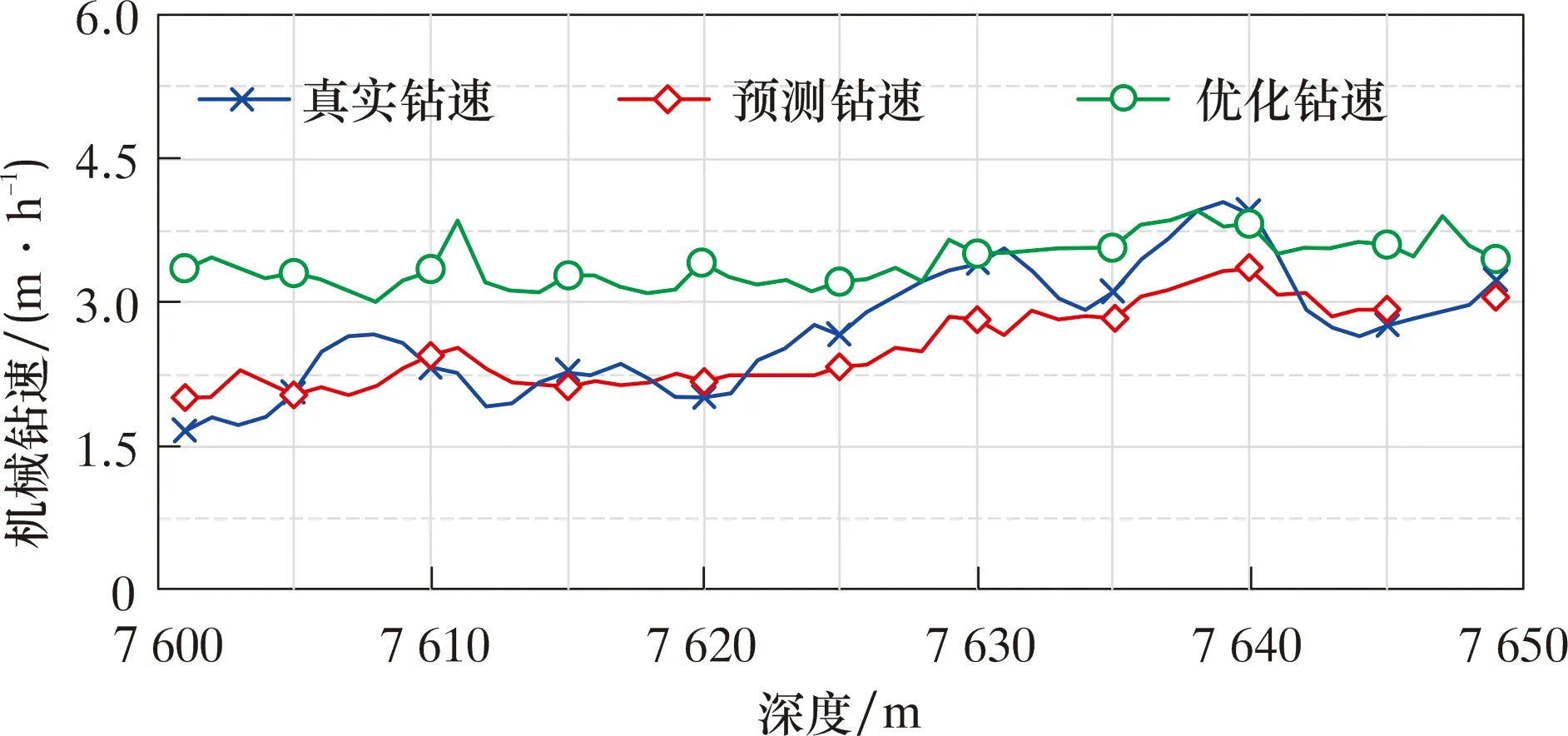
圖7 7 600～7 650 m水平段實際鉆速、預測鉆速和優化后鉆速對比Fig.7 Comparison of actual，predicted and optimized ROPs in 7 600 to 7 650 m horizontal section

圖8對比了7 600～7 650 m的真實機械比能和優化后機械比能。優化后機械比能相比優化前降低了約450 MPa，降幅達19%，且僅在7 639、7 640 和7 641 m處未達成優化效果，其原因與鉆速優化情況類似。因此，本文提出的協同優化方法在鉆速預測和鉆速-比能多目標優化方面都取得了較好的效果。

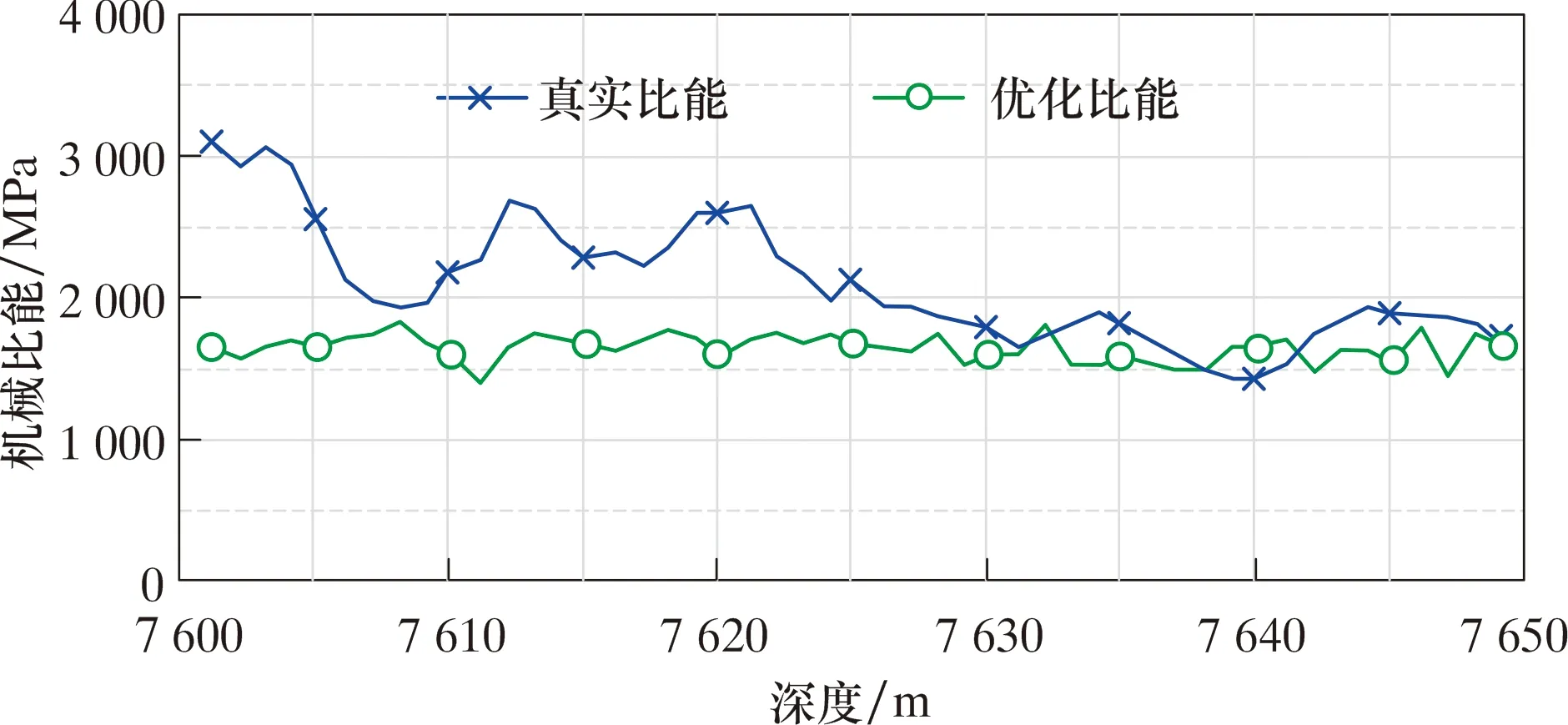
圖8 7 600～7 650 m水平段實際比能和優化后比能對比Fig.8 Comparison of actual and optimized specific energies in 7 600 to 7 650 m horizontal section

在風險約束方面，圖9與圖10為優化前后平均摩阻系數和平均巖屑床高度的對比。

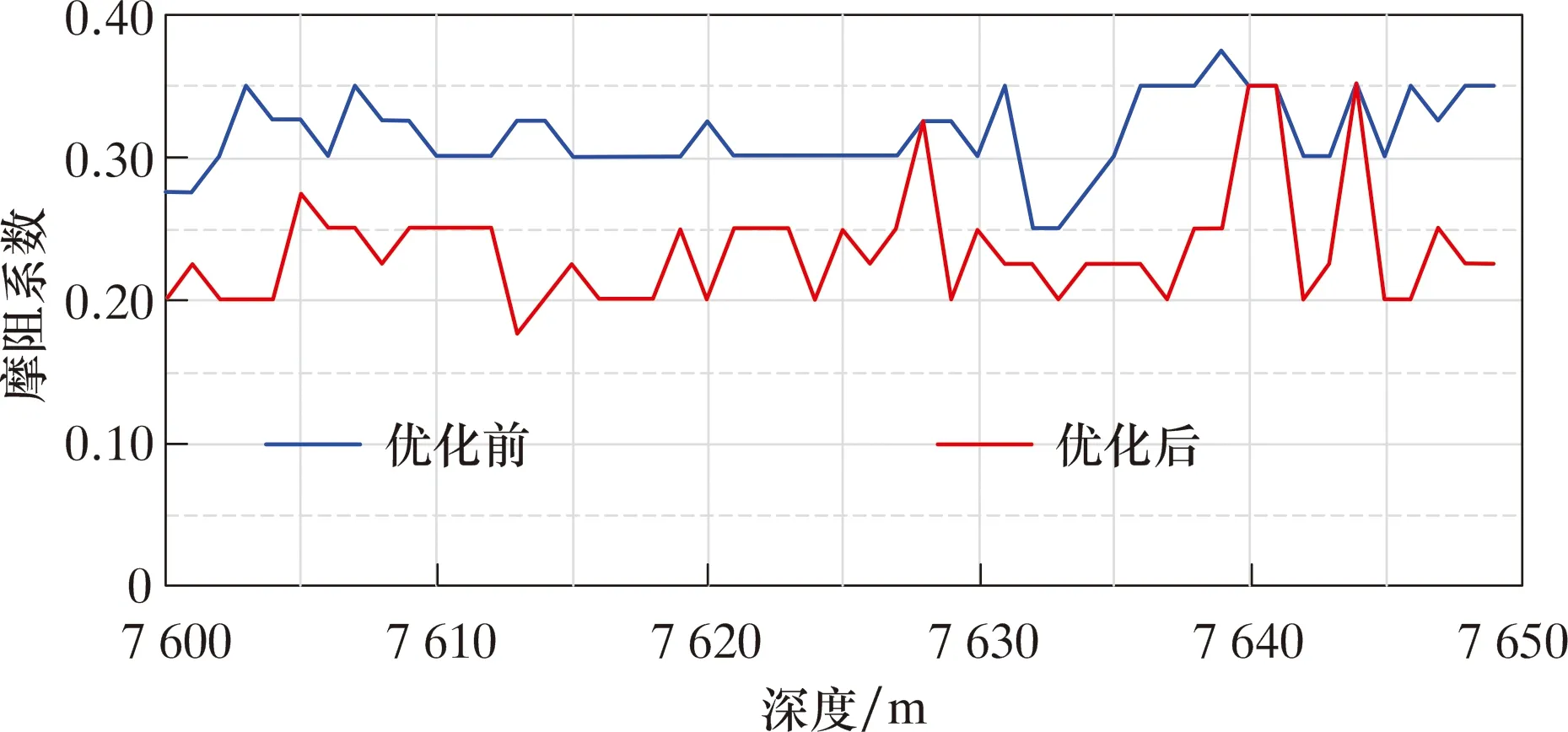
圖9 7 600～7 650 m水平段優化前、后平均摩阻系數Fig.9 Average friction coefficient before and after optimization of 7 600 to 7 650 m horizontal section

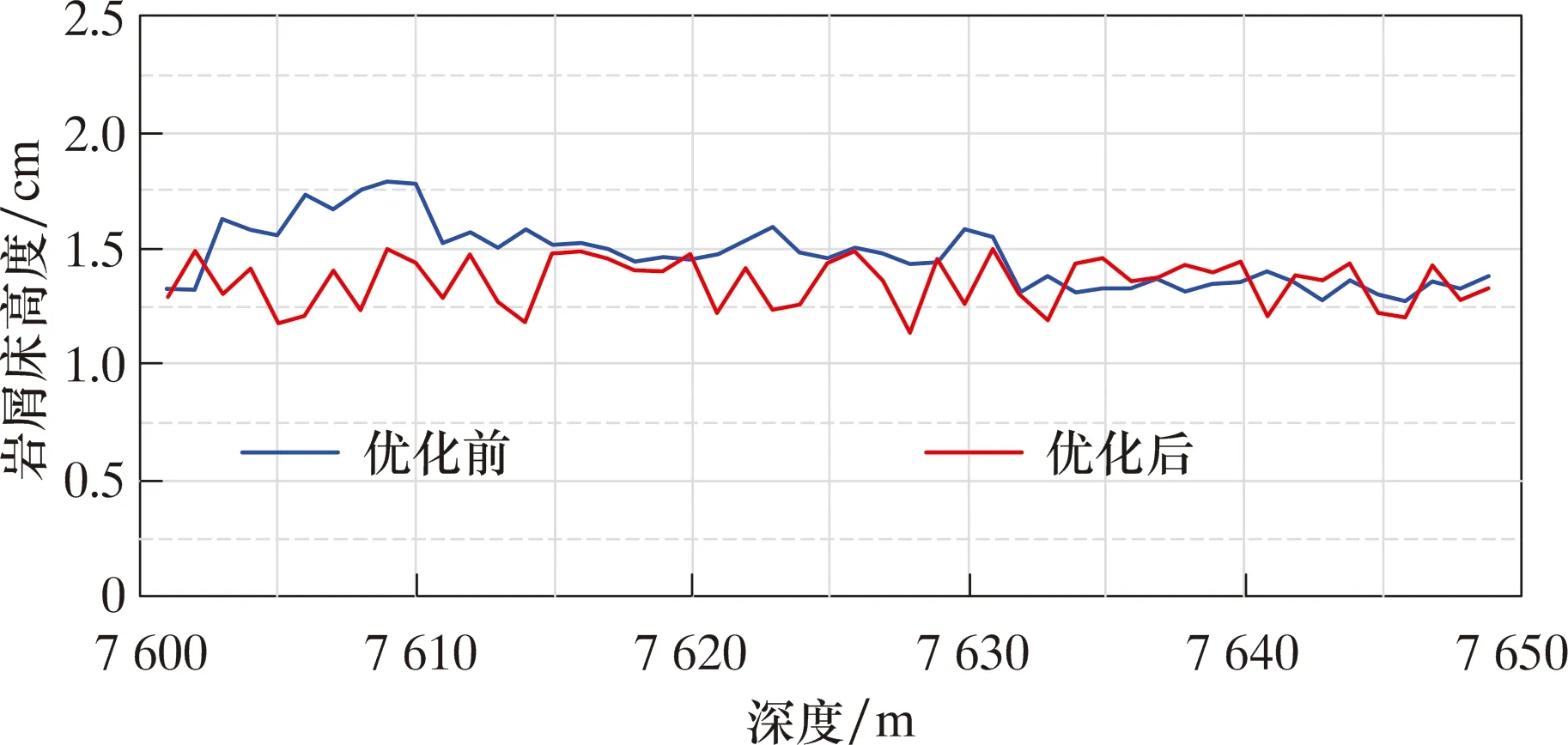
圖10 7 600～7 650 m水平段優化前、后平均巖屑床高度Fig.10 Average cuttings bed height before and after optimization of 7 600 to 7 650 m horizontal section

由圖9可知，優化前平均摩阻系數約為0.32，優化后為0.24，降低了25%。由圖10可知，優化前平均巖屑床高度為約1.47 cm，優化后約1.36 cm，降低了7.5%。表3對比了7 649 m處優化前、后的工程參數、效率指標和風險指標。相比優化前，鉆壓降低了11 kN，轉速基本保持不變，排量增大了14 L/s。可見，優化后機械鉆速和機械比能有少許提升，且由于鉆壓降低和排量提升，優化后相關風險指標有較大改善，表現在：優化后平均摩阻系數降低0.12，平均摩阻力減小38 kN，平均巖屑床高度降低0.15 cm。由此可見，在保證鉆進效率的同時減小了卡鉆、井眼清潔不足等風險。

表3 某井7 649 m處優化前、后工程參數和相關指標對比Table 3 Engineering parameters and related indicators before and after optimization at 7 649 m of a well

3 結束語

本文綜合考慮水平井鉆井破巖提速、管柱減阻和井筒清潔3個子系統協同作用，提出了鉆井過程協同優化方法。基于NSGA-Ⅱ和TOPSIS算法進行多目標優化決策，給出鉆壓、轉速和排量3個工程參數的推薦值。最后，以某水平井7 600～7 650 m水平段為例分析了其在機械鉆速預測、機械鉆速比能協同優化、風險約束等方面的效果。結果表明，該協同優化方法能夠提高機械鉆速、降低機械比能，且保證摩阻系數和巖屑床高度在安全范圍內，實現安全高效鉆進。

綜上所述，本文提出的水平井鉆井提速-減阻-清屑多目標協同優化方法能夠在優化鉆井效率的同時降低卡鉆和井眼清潔不足等風險，可為現場安全高效鉆進提供保障。建議后續可在以下方面改進：①采用3層模型，細化描述巖屑運移過程中流型變化的影響；②探索更高效的多目標優化與決策策略；③考慮井眼軌跡等其他鉆井子系統。