基于小波-LSTM的流溪河流域短期庫水位預測模型

張浩森，龍 巖，康愛卿

（1.河北工程大學水利水電學院，河北 邯鄲 056038；2.河北工程大學河北省智慧水利重點實驗室，河北 邯鄲 056038；3.中國水利水電科學研究院，北京 100038）

1 引言

水庫水位預報是防汛抗洪和水庫調度的基礎，高效精準的庫水位預測對水庫調度決策、降低災害風險具有重要意義[1]。然而，水庫水位變化受降雨量等諸多因素影響，水庫水文序列數據通常表現出顯著的時序性、復雜性和波動性等特征[2]，尤其是近些年氣象復雜多變，局部災害性天氣事件頻發，多流域洪水存在并發重發現象，水庫水位的快速變化也呈現增多趨勢，這使得庫水位預測面臨巨大的挑戰。

目前，對于庫水位預測的研究方法主要分為基于物理過程的水動力模型[3]和基于大數據的數據驅動模型[4]。水動力模型的精細化建模可以實現水位過程的精確模擬，其模擬精度也是當下最高的，但是水動力模型對地形等基礎數據要求較高，且存在計算資源消耗高、計算效率低等問題[5，6]。因而，研究采用基于大數據的數據驅動模型開展流溪河流域庫水位的短期預測。相較于傳統模型，數據驅動模型可以更有效地利用時序數據的時變特性[5]。其中，LSTM（長短時記憶神經網絡）模型利用自身的門控結構和細胞單元，解決了傳統ANN（人工神經網絡）在處理長序列數據時面臨的梯度消失或爆炸問題，對于長序列數據具備更好的預測效果，在水文長序列預測中已得到廣泛應用[7-11]。然而，基于小波-LSTM 模型的庫水位預測研究較少，因此，本文以流溪河流域的流溪河水庫和黃龍帶水庫為研究對象，構建了基于小波-LSTM 的流溪河流域短期庫水位預測模型，對不同預見期和不同輸入特征下的庫水位進行了對比分析，旨在為水庫水位預測提供參考。

2 研究區及數據

2.1 研究區概況

流溪河位于廣東省廣州市東北、北江和東江之間，干流全長約157 km，流域（113°10′12″E～114°2′00″E，23°12′30″ N～23°57′36″ N）總面積約2296 km2，年降雨量約1823.6 mm。降雨是流溪河流域水資源的主要來源，84%的降雨集中在汛期（4—9 月），因此流溪河流域降雨具有較強的季節性，且具有降雨強度大、范圍廣、暴雨頻繁等特點[12，13]。

流溪河流域建有完善的雨水情一體化監測體系，共有48 個主要的水庫監測站點和123 個雨量監測站點。綜合考慮流溪河流域內原始監測數據收集情況，選取流域內部的流溪河水庫和黃龍帶水庫為研究對象，研究區位置及監測站點分布如圖1所示。

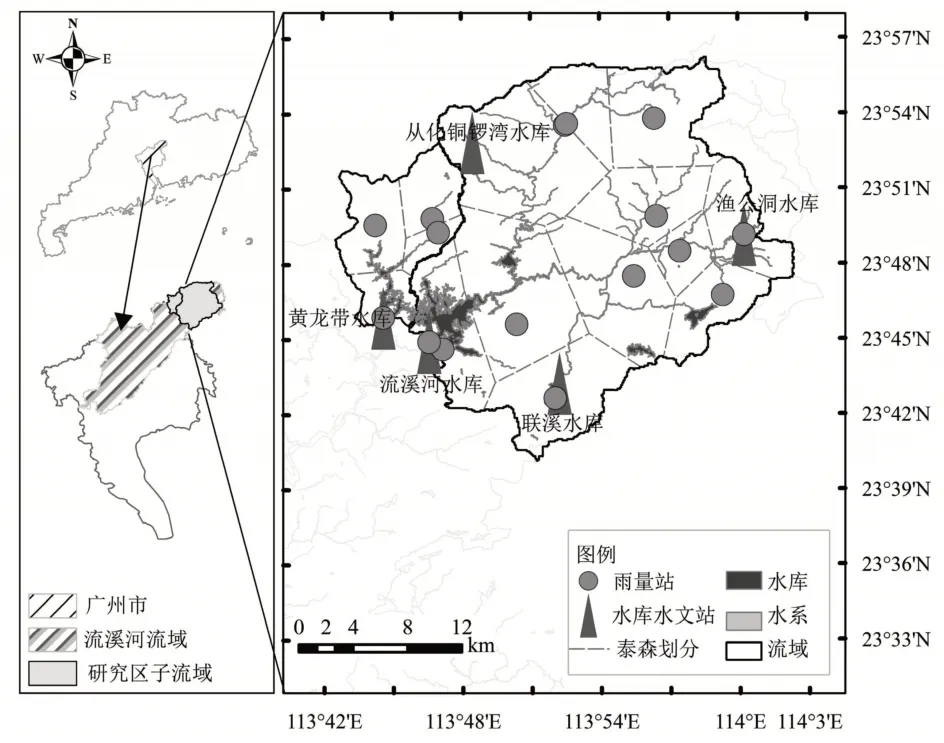
圖1 研究區位置示意

2.2 研究數據

研究采用ArcGIS 軟件進行子流域劃分和雨量站權重確定，并基于收集到的雨量站數據計算子流域面雨量。流溪河水庫和黃龍帶水庫雨量站權重，詳見表1。研究收集到的雨量、水位時序數據長度為2015年1 月1 日—2021年1月1日，時序間隔為1 h，序列數據以2019年8 月1 日為界進行數據集劃分。

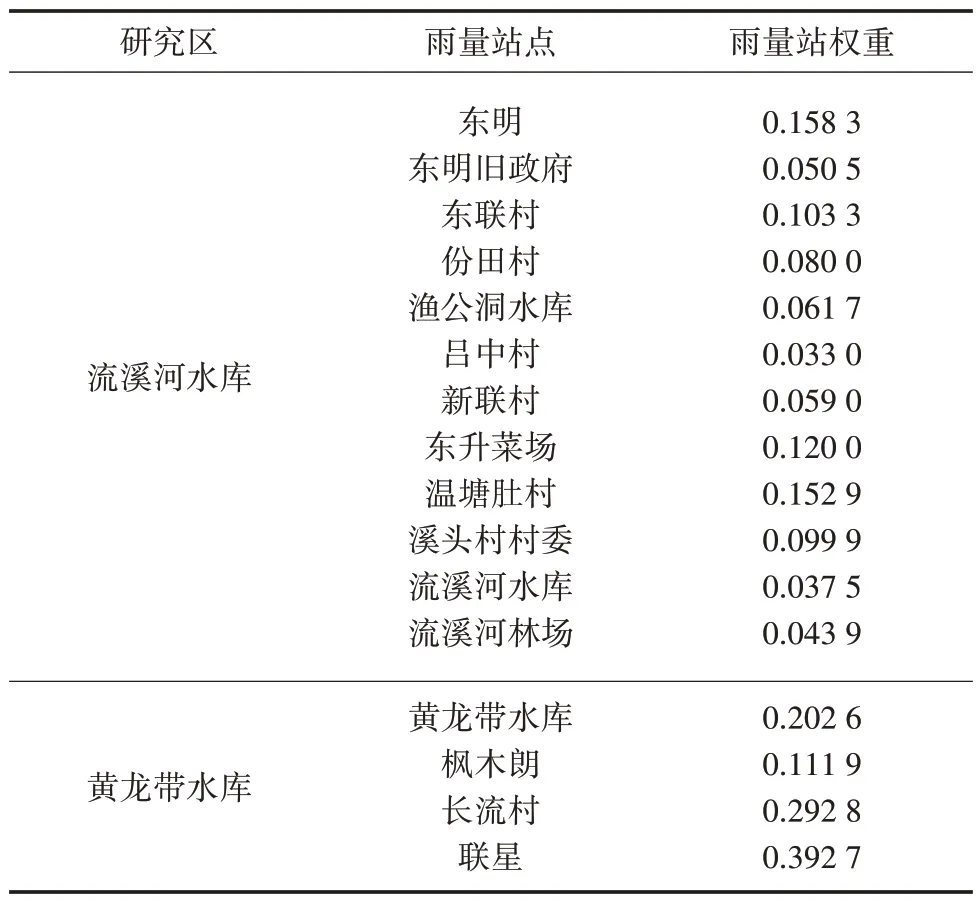
表1 研究區雨量站權重

3 研究方法

3.1 小波分解

小波分解是一種將數據轉換到同時帶有時域和頻域特征的方法，可以實現對時序數據的多尺度細化，達到高頻處時間細分、低頻處頻率細分。這種分解方式增強了局部信號的表現能力，提高了模型的抗噪性[9]，在一定程度上能提升模型精度。小波分解的具體實現可依據參考文獻[9]。

本研究采用離散小波對時序數據進行分解處理。考慮到db5小波更適用于分解比較光滑的連續數據集[9]，而經過數據清洗后的水位時序數據總體呈現光滑狀態。因而，研究采用db5 小波對流溪河水庫和黃龍帶水庫水位時序數據進行3 階分解，結果如圖2 所示。圖2 中S為原始水位時序數據，A3為db5 小波3 階分解后的低頻近似部分，D1、D2和D3為db5小波3階分解后的高頻細節部分。

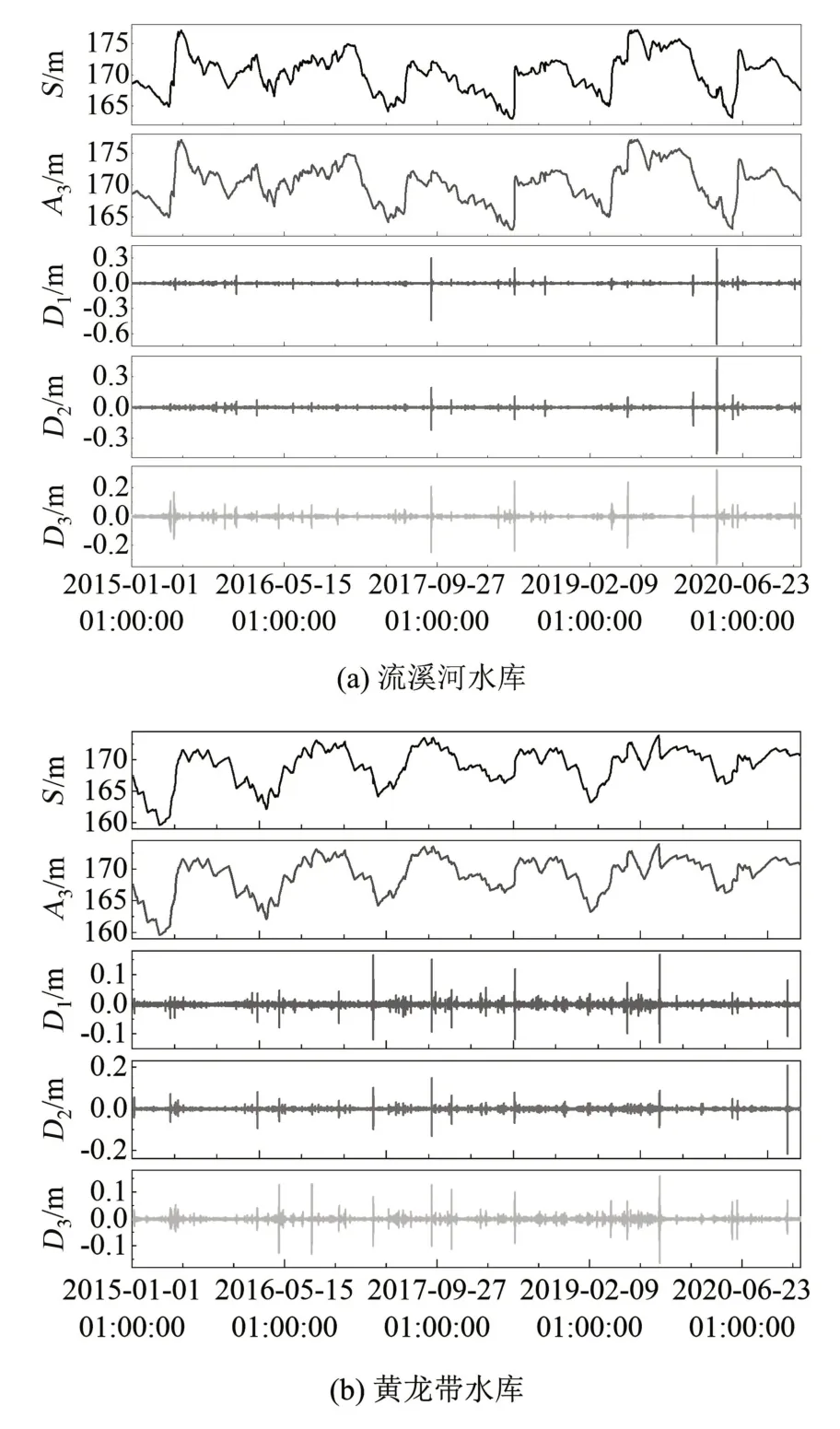
圖2 流溪河和黃龍帶水庫db5小波3階分解結果

3.2 LSTM模型

RNN（循環神經網絡）是用于時序數據分析的特殊神經網絡。然而，RNN 在時間步較長時會出現梯度消失現象，在狀態權重的模小于1 且時間步較短時梯度會出現爆炸現象，即RNN 對于短期依賴遠大于長期依賴，這使得RNN 難以處理長序列時間數據的預測。基于上述問題，LSTM（長短時記憶神經網絡）模型應運而生。LSTM 是一種引入門控單元和記憶細胞的特殊形式的RNN，LSTM 模型結構如圖3 所示。從圖3 可以看出，LSTM 模型通過門控結構和細胞單元控制傳輸狀態，即遺忘門（ft）決定了上一時刻單元狀態的保留程度，輸入門（it）決定了當前時刻網絡的輸入有多少可以保存到單元狀態，輸出門（Ot）則控制單元狀態，決定短期記憶流的呈現程度。這種特殊的結構解決了RNN中長期依賴問題，可以更有效地利用時序數據的時變特性。LSTM 模型的具體內部實現可依據參考文獻[6]。

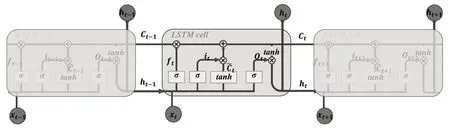
圖3 LSTM 模型結構示意

4 預測模型

4.1 數據預處理

模型構建前需對輸入數據進行數據清洗和數據變換[14，15]。數據清洗主要是時序數據的異常檢測和缺失插補。考慮到原始數據中的異常值大多為突增和突降異常，采用Adtk 異常檢測包中的LevelShift-AD突增突降檢測算法進行異常檢測，并對檢測出的異常值采取直接剔除處理。對于經過處理后的時序數據，采用隨機森林[16]的方式進行缺失插補。數據變換則是消除模型不同輸入特征數據間的差異，便于模型對輸入數據進行加權處理，對輸出數據進行對比分析。采用z-score 算法對數據進行標準化處理[14]，計算公式為：

式中：x為標準化后的序列數據；xo為原始序列數據；為序列均值；σ為序列標準差。

4.2 模型構建

本研究基于Tensorflow2.0、Python3.8 和Pycharm軟件進行水位預測模型構建。為研究小波-LSTM模型的預測精度，分別構建了基于單特征的流溪河水庫和黃龍帶水庫小波-LSTM 模型以及LSTM 對照模型。此外，考慮到流溪河水庫水位不僅受子流域面雨量影響，同時還受上游其余水庫站點影響，因而，為研究不同輸入特征對模型的影響，本研究以流溪河水庫為例，構建了流溪河多特征小波-LSTM 模型。其中，單特征是指模型僅以面雨量為輸入特征，多特征是指模型以面雨量和流溪河水庫站（黃龍帶水庫站）上游水庫水位站點的前期水位為輸入特征，單特征和多特征的預測項均是流溪河水庫站（黃龍帶水庫站）未來不同預見期下的水位。

基于上述模型框架，設置模型的輸出步長分別為1、6 和12 h，輸入步長分別為12、36 和72 h，以均方根誤差為損失函數，優化器選取Adam，模型中的網絡隱藏層單元數、學習率、每次運行樣本數和迭代次數由Python中的Hyperopt庫進行優化取值。

4.3 模型評價指標

納什效率系數（NSE）通常用于量化模型的預測精度，是一個無量綱的精度評估指標；平均絕對誤差（MAE）是一個存在量綱的模型精度評估指標，體現的是模型預測和實測數據之間的真實誤差，能有效地反映出預測結果的準確度；均方根誤差（RMSE）對模型預測數據中的異常值表現更為敏感，也是一個存在量綱的評估指標。在指標實際衡量過程中，RMSE的值越小則表征模型預測和實測數據之間的最大誤差越小，模型預測相對越準確。

綜上，為量化模型預測精度，使用NSE、MAE和RMSE3種量化指標，計算公式為：

式中：NSE為納什效率系數；MAE為平均絕對誤差（m）；RMSE為均方根誤差（m）；y?i為模擬數據（m）；yi為監測數據（m）；-y為監測數據均值（m）；N為樣本總數。

5 結果與分析

5.1 小波-LSTM模型預測結果評估

基于上述3種量化指標，小波-LSTM模型和LSTM模型對流溪河水庫和黃龍帶水庫測試集的預測結果詳見表2，模型預測與實測水位對比如圖4所示。

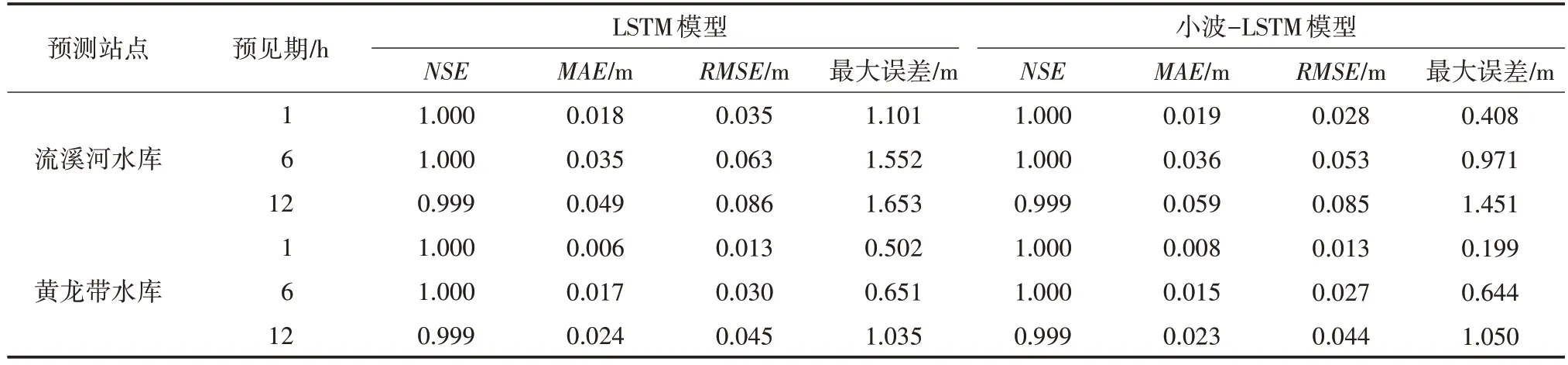
表2 模型測試集預測結果

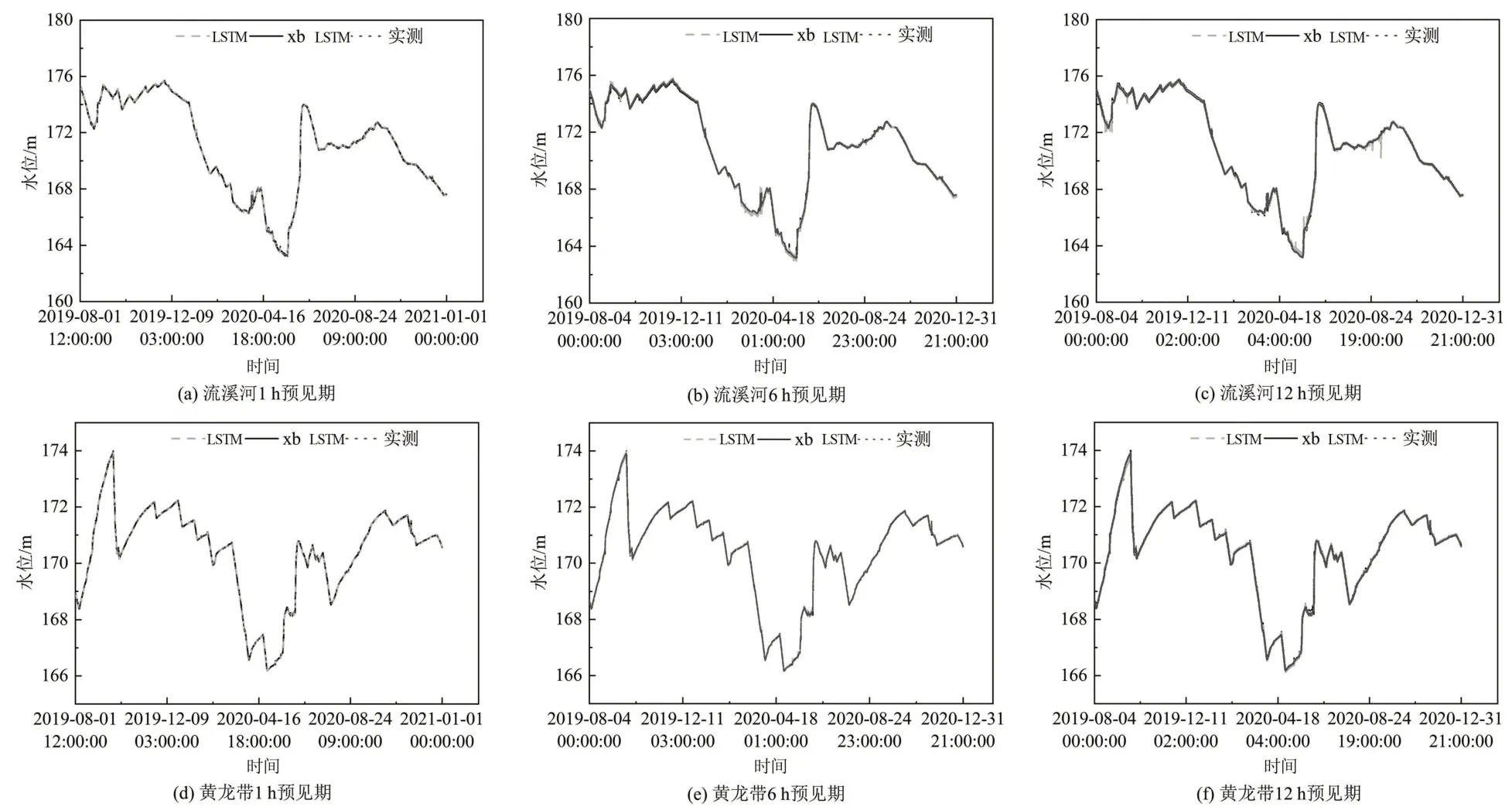
圖4 模型預測與實測水位對比

由表2和圖4可見：①隨預見期的增加，LSTM模型和小波-LSTM 模型的NSE均呈下降趨勢，MAE、RMSE和最大誤差均呈上升趨勢，但流溪河水庫和黃龍帶水庫的NSE均大于0.9，MAE和RMSE均保持在0.10 m 以下。結果表明，2 種模型對于流溪河水庫和黃龍帶水庫均具有很高的可信度，同時均取得不錯的預測效果。②就相同預見期而言，小波-LSTM 模型的NSE和LSTM 相差無幾，但小波-LSTM模型對應的RMSE和最大誤差大多都低于LSTM 模型。以1 h 預見期為例，流溪河水庫的LSTM模型的最大誤差超出小波-LSTM模型0.693 m，黃龍帶水庫的LSTM 模型的最大誤差超出小波-LSTM 模型0.303 m。結果表明，相同預見期下，小波-LSTM 模型預測的整體誤差和極值誤差均要優于LSTM 模型，模型的整體預測效果更優。

5.2 不同輸入特征情境下模型預測結果評估

以流溪河水庫為研究對象，小波-LSTM 模型在1、6 和12 h預見期下的模型預測結果詳見表3，模型評價指標對比如圖5所示。

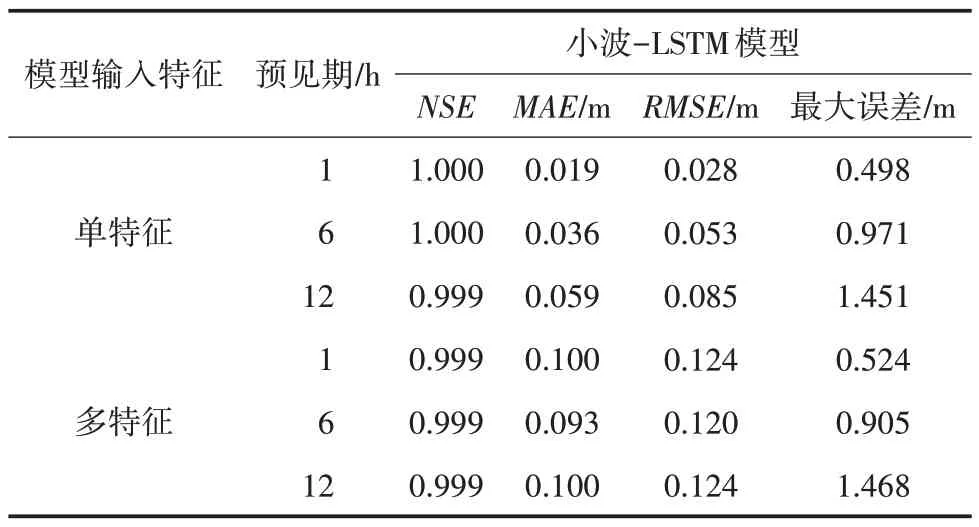
表3 模型訓練集預測結果

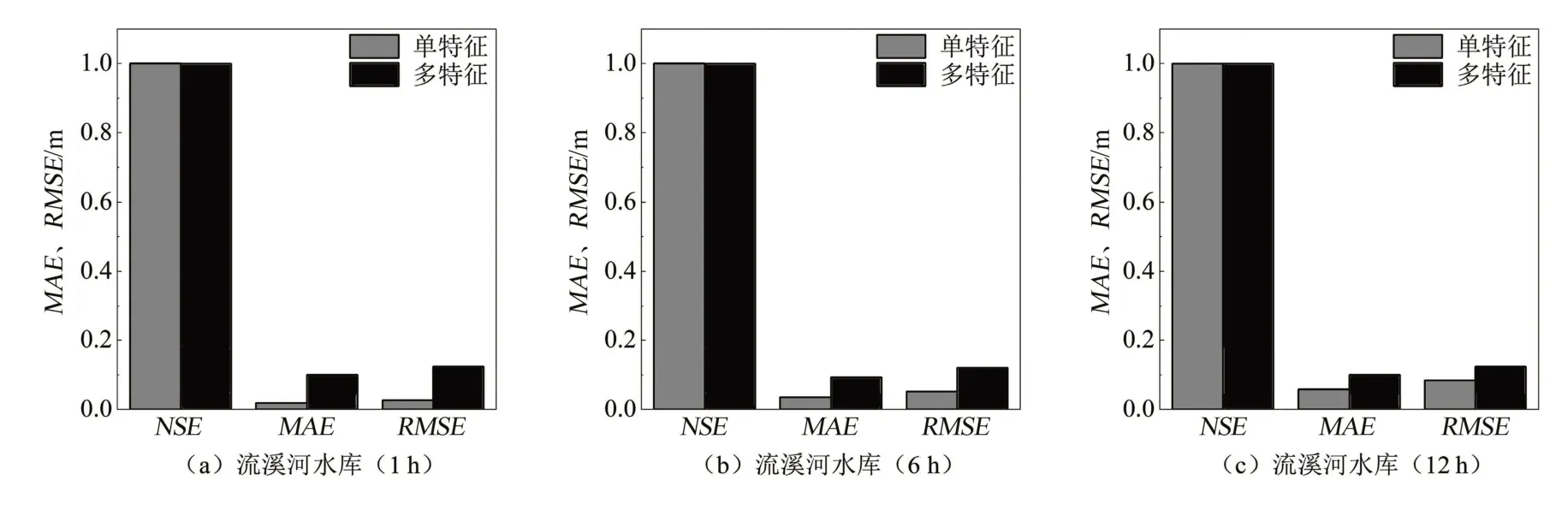
圖5 不同輸入特征下評價指標對比

由表3 和圖5 可見，就NSE而言，單特征小波-LSTM 模型和多特征小波-LSTM 模型相差無幾；就MAE和RMSE而言，單特征小波-LSTM 模型在1 h預見期下的最低值分別為0.019和0.028 m，在6 h預見期下的最低值分別為0.036 和0.053 m，在12 h 預見期下的最低值分別為0.059 和0.085 m；就最大誤差而言，單特征小波-LSTM 模型的最大誤差在1 h 預見期下要低于多特征模型，在6 和12 h 預見期下兩者則相差無幾。由此可見：①單特征小波-LSTM 模型對水位時序數據的整體預測誤差要低于多特征小波-LSTM 模型，對于水位時序數據的整體預測效果更好；②單特征小波-LSTM 模型的極值誤差要普遍低于多特征小波-LSTM 模型，即單特征小波-LSTM 模型對水位時序數據預測中的異常值相對少于多特征模型，單特征模型的最大預測誤差范圍要小于多特征模型，對水位時序數據極值的預測效果相對較優。

6 結論

（1）隨著預見期的增長，NSE下降，MAE和RMSE上升，表明模型預測精度與預見期呈負相關。

（2）小波-LSTM 和LSTM模型在1、6和12 h預見期下的NSE值均大于0.9，2 種模型均具有很高的可信度。但在相同預見期下，小波-LSTM 模型預測的整體誤差和極值誤差均小于LSTM 模型，模型的整體預測效果更優。

（3）單特征小波-LSTM 模型的整體預測誤差和極值誤差均低于多特征小波-LSTM 模型，對水位時序數據的整體預測效果更好，預測異常值更少。