基于節點重要度動態評估的復雜網絡級聯失效分析

姜敏勤, 石小晶, 楊鈺, 張正勇

(南京財經大學管理科學與工程學院, 南京 210023)

復雜系統可以抽象成各種與現實生活密切相關的復雜網絡,如社交網絡[1]、航空網絡[2]、交通網絡[3]及電力網絡[4]等。隨著復雜網絡研究的不斷深入,網絡的級聯失效行為作為復雜網絡研究領域的重要分支,學者對其的探索從未間斷。網絡的級聯失效是指當復雜網絡中的節點失效后,需根據相鄰節點間的耦合關系對失效節點的負載進行重分配,重分配過程可能會導致鄰居節點的負載超過自身的容量,從而發生鄰居節點連續失效的連鎖反應,導致網絡的部分癱瘓或是全面崩潰[5]。級聯失效現象讓現代社會依賴的各類網絡系統面臨嚴峻的挑戰,如2019年新冠肺炎疫情在中國武漢爆發,并迅速蔓延至全國各地,引發一系列的連鎖故障,尤其是其物流網絡接近癱瘓,對各行各業都造成了巨大的沖擊[6]。因此,網絡的穩定性和抗毀性問題已逐漸成為一個亟待解決且極具挑戰性的前沿課題。為有效預防和控制網絡的級聯失效現象,增強網絡的魯棒性,研究級聯失效具有極強的現實意義。

已有學者對復雜網絡的級聯失效行為進行了諸多探索,研究主要集中在級聯失效的建模及級聯抗毀性研究兩個方面。Motter等[7]首次提出了經典的線性容量負載模型來研究網絡的級聯失效,并指出具有高異質性負載分布的網絡在負載較高的節點受到攻擊時,容易引發級聯故障。Crucitti等[8]提出一個基于網絡流量動態重分配的級聯失效模型,指出一個負載最大的節點失效,便足以擊垮整個網絡。而Kim等[9]的研究發現網絡中容量較小的節點卻擁有較大的剩余容量,即真實網絡中的負載和容量并非是一種簡單的線性關系。基于此,竇炳琳等[10]對網絡的經典負載容量模型做出改進,以有效地抵御網絡的級聯失效。郝羽成等[11]基于節點過載狀態構建了一種級聯失效模型,指出節點負載的混合分配策略能夠有效控制級聯失效的影響。Ma等[12]提出一種新級聯失效模型,該模型基于度中心性和接近中心性來定義任意兩節點之間的連接負載,以增強無標度網絡的魯棒性。劉鳳增等[13]給出了一種考慮資源限制的節點負載分配方式,研究級聯失效下非對稱依賴網絡的魯棒性,指出根據度值分配節點容量的網絡魯棒性更強。謝本凱等[14]建立了一種考慮節點狀態的民航網絡容量負載模型,指出應注重增強網絡關鍵節點的魯棒性,以保證網絡的安全運行。Feng等[15]提出一種匹配級聯失效模型來同時分析節點和邊的潛在過載,研究表明在無標度網絡中,一個關鍵節點的故障可能會導致整個網絡的崩潰。高潔等[16]提出一種基于非線性容量負載模型,研究具有電氣特征的加權電網和只具有拓撲結構的無權電網,分別面對網絡級聯故障時的抗毀性情況。

縱觀已有研究,多側重于探討如何定義網絡節點的初始負載和容量,以及容量的分配策略等方面,鮮有研究關注級聯失效過程中網絡節點重要性的度量,普遍認為度值較高的節點更為重要,在級聯失效仿真過程中,較多采用度值攻擊策略,即優先攻擊度值較高的節點,但根據單一指標評估節點的重要度有一定的局限性。而現有的其他節點重要性度量方法[17-19],雖已取得諸多進展,但基本還停留在網絡的靜態層面,鮮有報道研究級聯失效過程中網絡結構隨節點失效呈現出變化的動態特性,且重要度不同的節點受到攻擊會對網絡抗毀性大小的變化存在不同程度的影響,故尚未深刻揭示節點重要性動態規律。因此,現提出一種基于網絡結構實時狀態演化的節點重要度評估方法,以提高重要節點評估方法的科學性及后續級聯失效仿真分析的可靠性,在此基礎上引入兩個容量參數,分析網絡節點負載與容量間的非線性行為,并提出一種新的節點攻擊策略,以保證每次仿真實驗攻擊的節點都是當下網絡中最重要的節點,對網絡抵制級聯失效的抗毀性進行深入研究。

1 復雜網絡節點重要度評估方法

復雜網絡中的重要節點對分析網絡的結構和功能,增強網絡魯棒性和穩定性至關重要。為挖掘網絡中的重要節點,現提出一種基于灰色關聯法和多準則妥協解排序法(VIKOR),綜合考慮節點的度中心性、介數中心性和接近中心性的重要節點評估模型。

(1)構建評價決策矩陣。根據文獻[20]計算節點的度中心性指標、介數中心性指標和接近中心性指標值,構建網絡節點重要性評估的決策矩陣X,即

(1)

式(1)中:Xij為節點i的第j個中心性指標;n為節點數;m為中心性指標個數。

(2)標準化決策矩陣。由于中心性準則之間存在維度差異,需對矩陣進行標準化處理[21],處理后的標準化決策矩陣為D=(dij)n×m,計算公式為

(2)

(3)計算各中心性指標的權重。采用客觀賦權法中的熵權法,利用中心性準則之間的關聯程度和提供的信息來確定權重wj,計算公式為

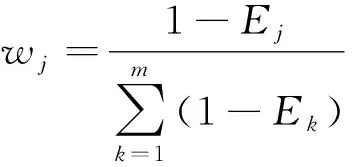
(3)

式(3)中:Ej為中心性準則j的信息熵。

(4)確定正負理想解。根據標準化決策矩陣,確定正理想解d+和負理想解d-,計算公式為

(4)

(5)

式中:J為效益型指標;O為成本型指標。

(5)采用歐氏距離計算各節點的初始群體效用值Si和個別遺憾值Ri,公式為

(6)

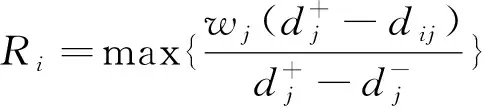
(7)

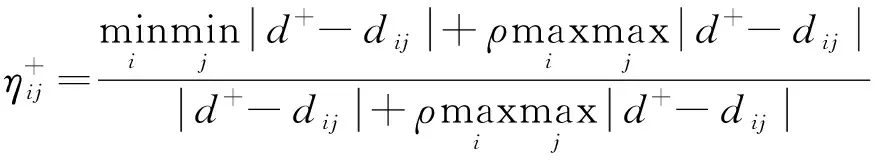
(8)

(9)

式中:i=1,2,…,m;j=1,2,…,n;ρ為分辨系數,一般ρ=0.5。

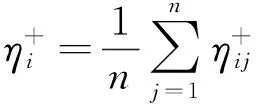
(10)

(11)

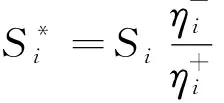
(12)

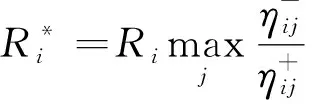
(13)

(9)確定各節點的綜合評估值Qi,公式為

(14)

2 級聯失效模型

2.1 初始負載

初始負載反映了節點在某一時刻處理信息的能力[22]。已有的研究往往以度值[23]或介數值[24]來定義節點的初始負載,但網絡節點的有效運行也依賴于其他鄰居節點[25],故設置節點的初始負載為

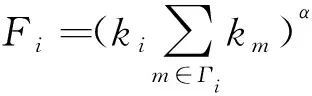
(15)

式(15)中:Fi為節點i的初始負載;ki為節點i的度值;Γi為節點i的鄰居節點的集合;α為調節初始負載強度的參數,α>0。

2.2 節點容量

一個節點的容量是其能承受的最大負載。根據Motter-Lai模型,一個節點的容量與該節點的初始負載呈線性關系,但在真實的網絡中,容量和負載表現出一種非線性關系,為保證節點容量的模型更接近真實的復雜系統,定義節點容量為

Ci=Fi+θFiβ

(16)

式(16)中:Fi為節點i的初始負載;Ci為節點i的最大容量;θ和β為控制節點容量的容量參數,且有θ>0,β>0 ;當β=0時,該模型轉化為經典的Motter-Lai模型。

2.3 負載重分配模型

當節點的負載超過了節點自身的最大容量時,則該節點會發生故障,從而引起負載的重分配。本文中采取與節點的初始負載成比例的重分配方式將故障節點的負載分配給鄰居節點,表達式為

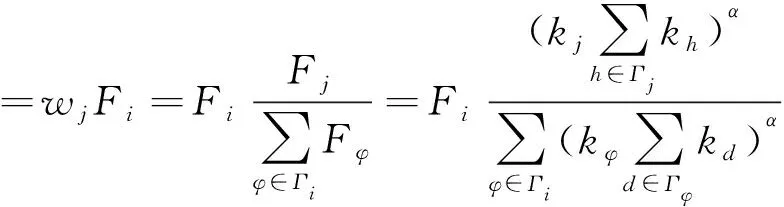
(17)

式(17)中:ΔFj為鄰居節點j增加的負載量;wj為負載的分配比例;Γi為節點i的鄰居節點的集合。

此時,鄰居節點j的實時負載為

Fj(t)=Fj(t-1)+ΔFj

(18)

式(18)中:Fj(t)為節點j的t時刻的實時負載;Fj(t-1)為t-1時刻節點i沒有失效時的實時負載。若Fj(t)>Cj,節點j也會失效,則進行失效節點j的二次負載重分配,直至相鄰節點所分配到的負載與初始負載之和滿足其最大容量限制。若Fj(t)≤Cj,則級聯失效中斷。

2.4 抗毀性測度指標

最大連通子圖指網絡受到攻擊,被分為若干個子網絡后的最大連通分量,而最大連通子圖比例指網絡受到攻擊后,網絡最大連通子圖的節點數與初始網絡節點數量的比值[26]。本文中采用最大連通子圖比例來量化復雜網絡的抗毀性,計算公式為

(19)

式(19)中:S為最大連通子圖的比例,S越大,表示網絡的魯棒性越強[27];N′為最大連通子圖所包含的節點數;N為網絡總節點數。

上述級聯失效算法流程如圖1所示。

3 仿真實驗與分析

為驗證所提方法的有效性和可靠性,選擇以《成渝地區城際鐵路建設規劃 (2015—2020年)》的數據為例,繪制其網絡拓撲圖如圖2所示,進行仿真分析。文獻[28]表明,成渝地區鐵路網絡具有小世界特性和無標度特性,且與京津翼和西北地區的鐵路網絡相比,具有更為明顯的復雜網絡特性。

圖2 成渝地區鐵路網絡拓撲圖Fig.2 Topological map of intercity railway network in the Chengdu-Chongqing region

3.1 靜態節點重要性評估

根據式(2)～式(14)計算出節點重要性指標數值如表1所示,由于網絡節點數較多,只展示重要度排名前20的節點。

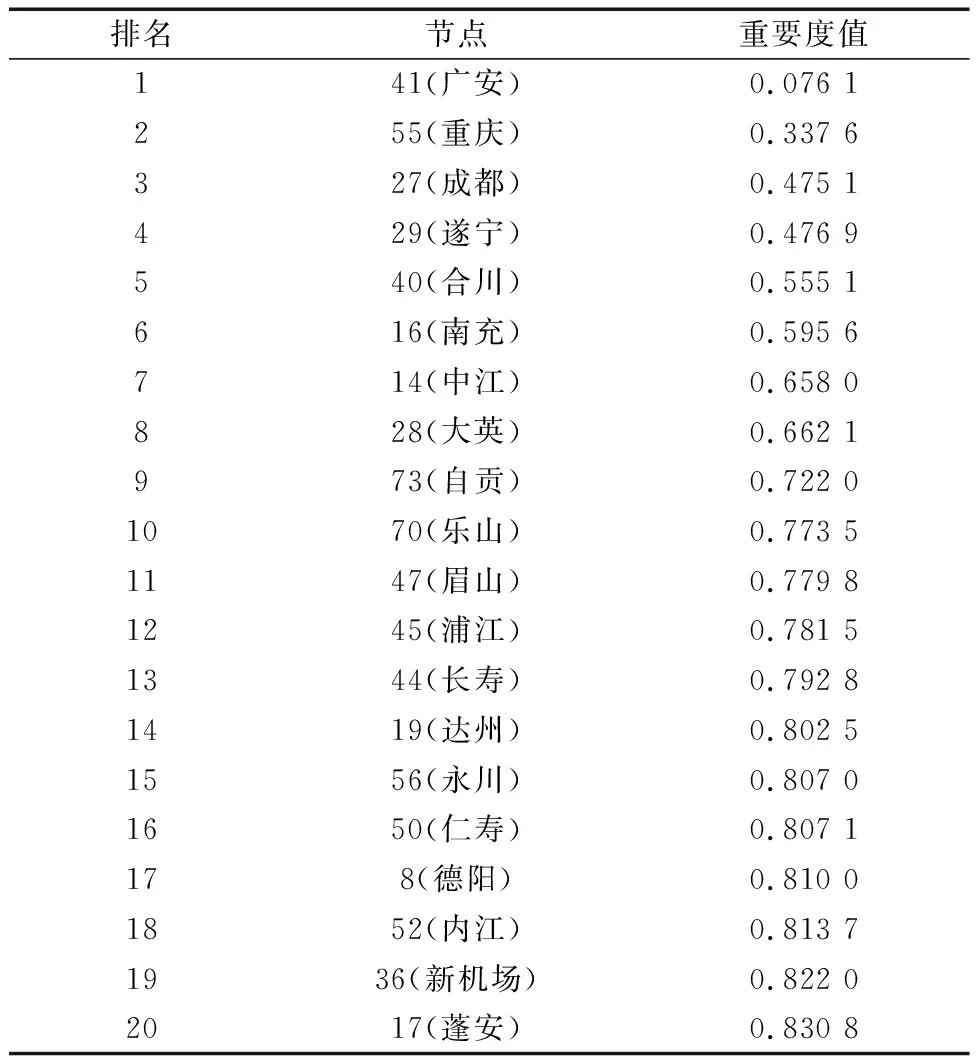
表1 靜態評估下節點重要度排名前20的節點排序Table 1 Ranking of the top 20 nodes in terms of node importance under static evaluation

由表1可以看出,節點41所在的城市——廣安是成渝地區鐵路網絡中最關鍵的節點,其雖然度值只有3,但是網絡中大部分節點間的最短路徑都會途徑該節點,且廣安的鄰居城市重慶和南充的重要度排名均相對靠前,進一步強化了廣安在整個鐵路網絡中的重要性,使其成為網絡中控制信息傳輸的關鍵位置。從鐵路運輸的現實意義來看,若廣安喪失正常的運轉功能,會使得部分城市間的鐵路運輸距離大大增加,從而導致鐵路網絡運輸的效率大幅下降。節點55(重慶)、節點27(成都)、節點29(遂寧)、節點40(合川)和節點16(南充)在網絡中的各項中心性指標均相對較大,位于網絡中心位置,連接多個節點城市,具有重要的樞紐作用。節點14(中江)、節點73(自貢)、節點70(樂山)、節點45(浦江)、節點19(達州)、節點56(永川)、節點8(德陽)雖靠近網絡的邊緣位置,但是其重要度排名依舊靠前,這是由于這類節點坐落于成渝地區與省會中心城市(重慶和成都)的連接處,其介數中心性、度中心性和接近中心性指標值都相對較高,若此類節點發生故障,則會在一定程度上影響邊緣城市與中心城區的聯系。

采用隨機攻擊、重要度攻擊、度值攻擊以及介數攻擊4種攻擊策略,攻擊成渝地區鐵路交通網絡,根據最大連通子圖比例的變化情況反映網絡的受損程度,以初步驗證節點重要度評估模型的有效性。隨機攻擊是通過python編程隨機生成節點的序列,依次對網絡進行攻擊;蓄意攻擊則是根據前文方法得到的節點排序,依次對網絡進行攻擊;度值攻擊和介數攻擊為按節點的度中心性和介數中心性從大到小的順序排序,依次對網絡進行攻擊。最大連通子圖的變化情況如圖3所示。

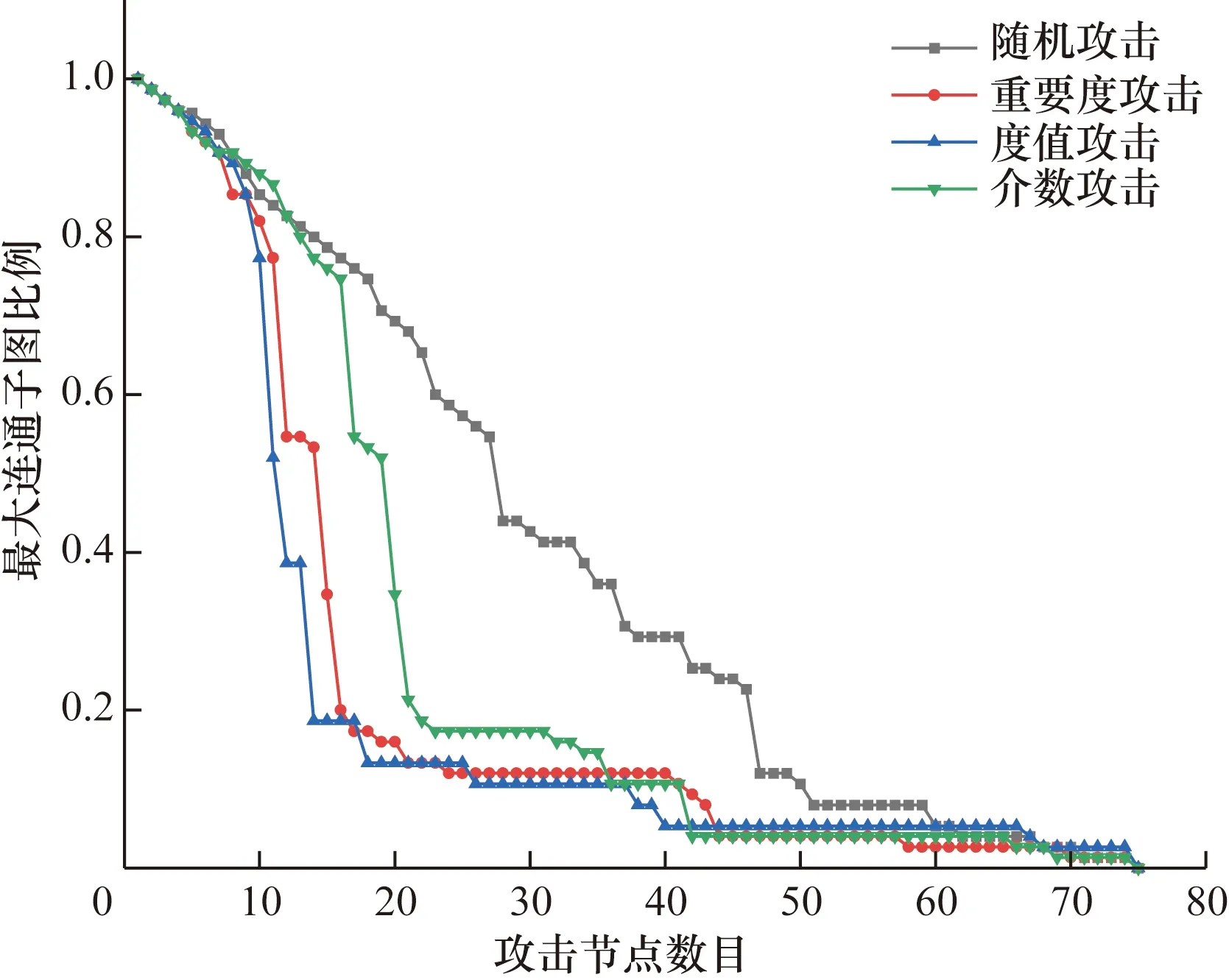
圖3 靜態攻擊下最大連通子圖比例變化情況Fig.3 Changes in the proportion of the maximum connected subgraph under static attack

從圖3可以看出,網絡受到隨機攻擊時,最大連通子圖比例下降的速度較為緩慢,累計攻擊20個節點,網絡的最大連通子圖比例才降至70.7%。表明小范圍內的節點失效并不會對網絡的整體連通性造成較大的影響,但當移除的節點數目達到一定規模時,也會使網絡剩余的節點變成孤點。網絡在度值攻擊下的靜態抗毀性最差,網絡最大連通子圖比例下降最快,累計攻擊15個節點時,最大連通子圖比例下降至18.7%,說明網絡節點的度中心性最能代表節點在靜態網絡拓撲結構中的重要程度。在介數攻擊下,累計攻擊18個節點時,網絡的最大連通子圖的比例才降至18.7%,累計攻擊24個節點時,網絡接近崩潰。在重要度攻擊下,網絡表現的靜態抗毀性與度值攻擊下的大致相同,當受攻擊的節點數少于12個時,最大連通子圖的比例并沒有明顯的下降,這是由于節點重要度排名前12的節點均具有較大的度值,即周圍的鄰居節點比較密集,節點失效后,可以找到可替代路徑疏通網絡,所以并不會在很大程度上降低網絡的連通性。當累計攻擊12個節點時,最大連通子圖比例驟降到54.7%,網絡連通性受到較大的影響,當被攻擊的節點數量達到15個時,最大連通子圖比例急劇下降到20%,大大降低了網絡的連通度和可達性,這是由于受到攻擊的節點是發揮連通網絡作用的關鍵節點,這些節點的故障導致網絡受到重創被分裂成多個子網絡,無法實現跨城區的運輸。

3.2 動態節點重要性評估

考慮網絡靜態特性下的節點重要性評估已取得了諸多進展[29],但實際網絡的結構會隨節點所受的攻擊而發生改變,根據初始網絡數據評估出的重要節點,當下可能已經不再重要。為提高方法識別的精確性及后續級聯失效仿真分析的可靠性,應每當一個節點受到攻擊失效后,就重新計算網絡節點的重要度,以保證每次攻擊的節點都應是當前網絡最重要的節點,采用上述動態評估方法得到成渝鐵路網絡中,節點重要度排名前20的節點如表2所示。

由表2可以看出,動態評估模式下得到的節點重要度排名與根據網絡初始狀態得到的節點重要度排名有較大的出入,由于鐵路網絡的初始拓撲結構相同,故節點41(廣安)無論是在網絡的靜態還是動態特性下,都是成渝鐵路網絡中最關鍵的節點,節點41(廣安)失效后,在更新后的網絡拓撲結構中,節點55所在的城市——重慶成為當下網絡下最關鍵的節點,重要性僅次于節點41,這與靜態評估模式下的排名相同。但后續的節點重要度的排名變化較大,節點27(成都)在動態評估模式下,其重要性排名從第3降至第7,而節點52(內江)的重要度則從第18升至第4,在靜態評估下重要度排名前20的節點中,節點14(中江),節點28(大英),節點45(浦江),節點44(長壽),節點56(永川)均未進入動態評估模式下節點重要度排名前20中,說明這些站點在成渝鐵路網絡的關鍵站點受到攻擊后,已經不再是網絡的關鍵節點,可見,網絡節點的重要度是伴隨網絡拓撲結構的變化而發生改變的,進一步驗證了進行網絡節點重要度動態評估的必要性。

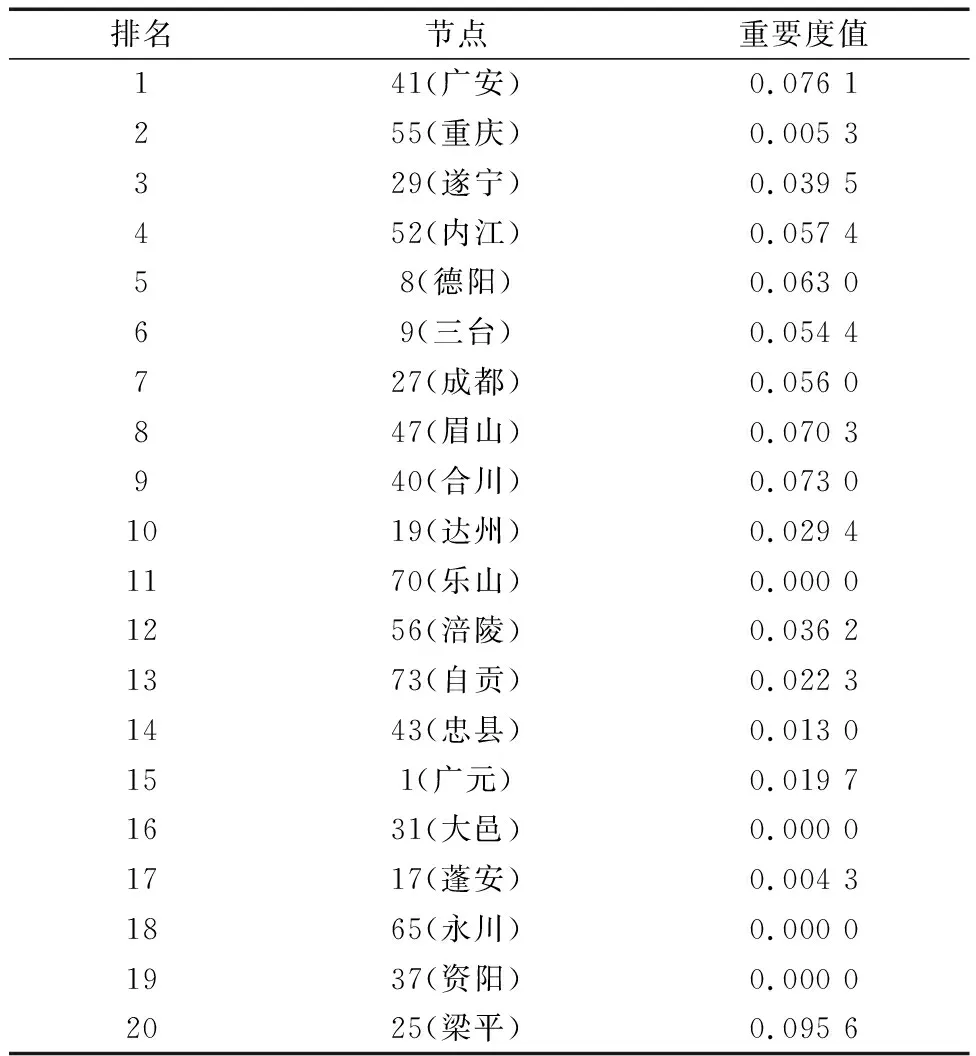
表2 動態評估下節點重要度排名前20的節點排序Table 2 Ranking of the top 20 nodes in terms of node importance under dynamic evaluation

為對比分析,采用隨機攻擊、重要度攻擊、度值攻擊以及介數攻擊4種攻擊策略,其中重要度攻擊、度值攻擊和介數攻擊均為根據網絡的實時狀態計算得到,累計攻擊20個節點。得到網絡最大連通子圖比例隨攻擊節點數目的變化情況如圖4所示。

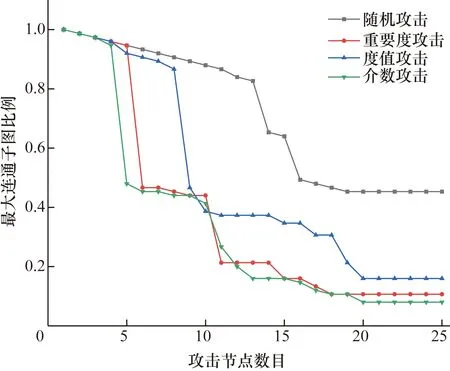
圖4 動態攻擊下最大連通子圖比例變化Fig.4 Maximum connected subgraph scale change under dynamic attack

如圖4所示,在不考慮級聯失效情況下,從網絡的連通性而言,網絡面對隨機攻擊時,網絡依舊表現出較好的魯棒性,但當面臨蓄意攻擊時,則表現出更為明顯的脆弱性。其中,根據介數攻擊網絡節點時,網絡下降的趨勢最快,累計攻擊5個節點,最大連通子圖的比例便下降至48%。從度值攻擊策略來看,累計攻擊9個節點時,最大連通子圖比例值才降至46.7%,累計攻擊19個節點時,網絡接近崩潰。在重要度攻擊策略下,其最大連通子圖比例值的下降趨勢與介數攻擊策略下的非常相似,當6個網絡節點受到攻擊時,網絡的最大連通子圖比例驟降至46.7%,被攻擊的節點數量達到11個時,最大連通子圖比例驟降至21%,此時網絡的連通性和可達性已經受到了嚴重影響。與度值攻擊策略相比較,重要度攻擊策略可以更快速地使網絡崩潰,這表明采用動態的節點重要度計算方法,可以有效提高關鍵節點識別的精確性。

3.3 基于動態節點重要度評估的級聯失效分析

考慮級聯失效情況下,設置參數α=0.2,β=0.5,θ=0.8。同樣采用隨機攻擊、重要度攻擊、度值攻擊以及介數攻擊4種攻擊策略,得到最大連通子圖比例的變化情況如圖5所示。可以看出,重要節點在網絡中的作用相較于非級聯失效情形更為突出。網絡面對隨機攻擊時,最大連通子圖下降的趨勢較為平緩,但累計攻擊一定數量的節點后,則會出現級聯失效的現象,可能是因為攻擊到網絡中的關鍵節點,導致網絡中大部分剩余節點變成孤點,從而引起最大連通子圖比例值的急劇下降。網絡面對蓄意攻擊下,當攻擊節點達到5個時,介數攻擊策略下的最大連通子圖的比例迅速下降至47.3%;當失效節點達到8個時,度值攻擊策略下的最大連通子圖比例驟降至2.63%;攻擊9個節點時,度值攻擊策略和介數攻擊策略下的最大連通子圖比例值均下降到0,說明每一輪攻擊后,度值和介數較大的節點都有可能是網絡的關鍵節點,這些關鍵節點的失效引發了多輪負載重新分配過程,這也進一步驗證,節點的重要度評估不能只關注網絡單一屬性指標,應考慮多個指標進行綜合評估。網絡面對重要度攻擊策略時,最大連通子圖比例變化最為明顯,僅攻擊一個節點時,對網絡的連通性沒有造成太大影響,但累計攻擊2個節點后,網絡便迅速崩潰,最大連通子圖比例驟降至0。攻擊的前2個節點分別為節點41和節點55,就第2個受攻擊的節點55而言,其度值最大,即周圍的鄰居節點較多,但其大部分鄰居節點的度值較小,且部分鄰居節點之間又互為鄰居節點,根據級聯失效的初始負載及負載分配策略的定義來看,由于節點55的初始負載較大,且攻擊的第一個節點41也是節點55的鄰居節點,節點41失效之后,節點55又承接了來自失效節點41分配的額外負載,這就導致該節點受到攻擊之后,其周圍的鄰居受到節點最大容量的限制,無法承接來自節點55分配的高額負載,從而引發級聯故障,使最大連通子圖比例值突變為0。

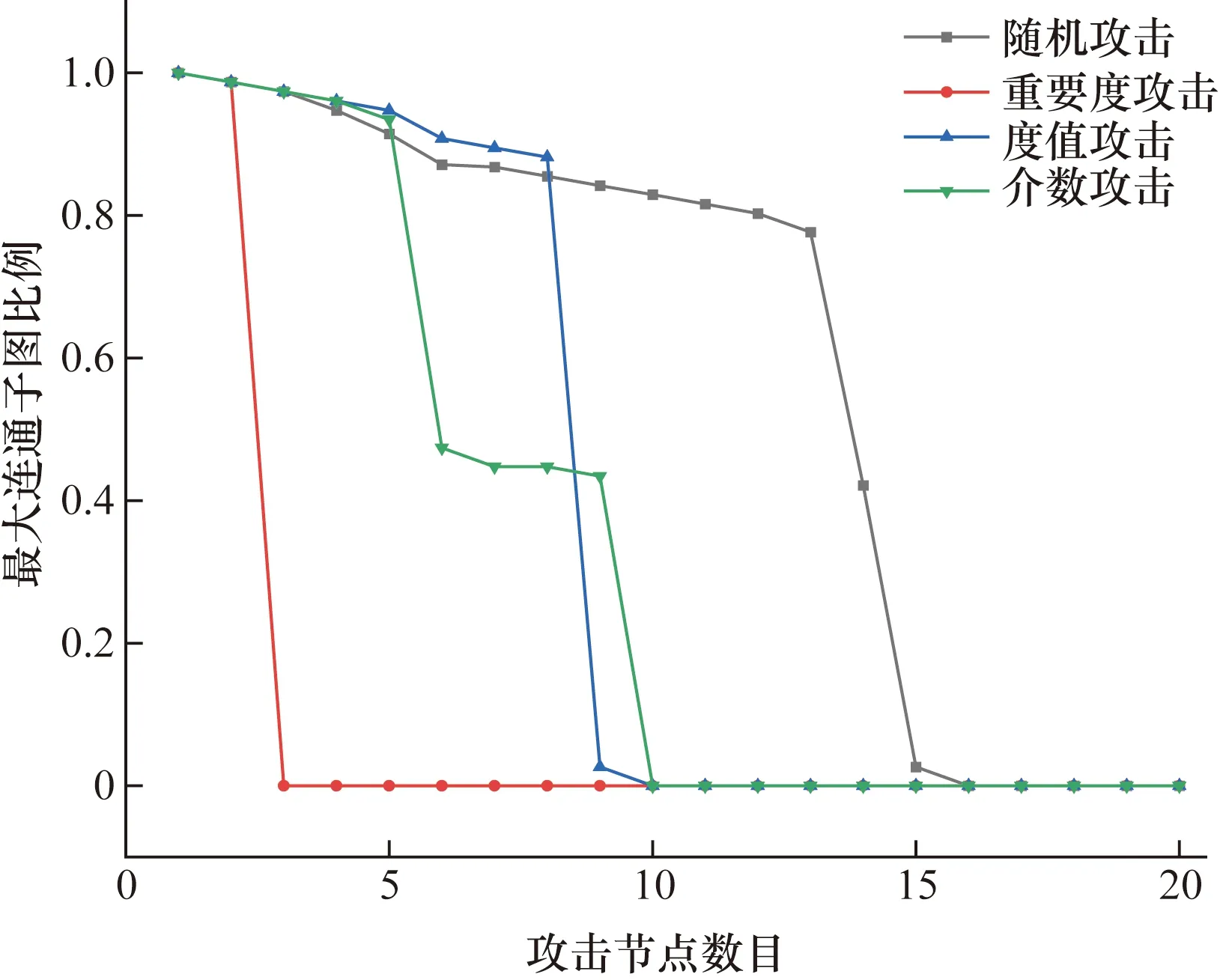
圖5 級聯失效下最大連通子圖比例變化Fig.5 Proportional change of maximum connected subgraph under cascade failure

3.4 模型參數對網絡級聯失效魯棒性的影響

級聯失效模型中包含α、θ和β共3個參數,采用重要度攻擊策略,探究參數對級聯失效下網絡魯棒性的影響。參數α用于控制節點初始負載的強度。設置β=0.9,θ=0.8,令α∈[0.1,0.9],得到最大連通子圖比例的變化情況如圖6所示。當α∈[0.1,0.3]時,最大連通子圖比例曲線沒有明顯的變化趨勢,但網絡表現出一定的脆弱性,且α=0.2時,網絡的抗毀性最差,這說明當參數α∈[0.1,0.3]時,可能存在一個邊界值,導致網絡在抵制級聯失效時表現出一定的脆弱性。當α≥0.4時,最大聯通子圖比例曲線迅速上移,此時網絡具有較強的抗毀性,且趨于穩定,說明當α超過某一閾值時,最大連通子圖比例對于網絡級聯失效所帶來的影響反應減緩,能在一定程度上提高網絡的抗毀性。

圖6 不同α下的最大連圖子圖比例變化情況Fig.6 Variation of the proportion of maximum contiguous subgraphs for different values of α

β和θ都是用于控制節點最大容量的容量參數,為探究容量參數對網絡抵御級聯失效的抗毀性的影響,令α=0.4,β=0.9,得到參數θ不同取值對網絡最大連圖子圖比例的演化情況如圖7所示。可以看出,隨著θ取值的增大,網絡最大聯通子圖比例曲線逐漸右移,當θ≥0.7時,級聯失效的臨界值較大,此時網絡有較好的抗毀性,網絡受到攻擊也不會導致最大連通子圖比例曲線有較大的波動。

令α=0.4,θ=0.8,在實驗中,當0<β≤0.3時,由于節點的容量較小,導致網絡的抗毀性較差,僅攻擊一個重要節點,網絡便迅速崩潰,且最大連通子圖比例曲線均與β=0.4時相重合,故取β∈[0.4,1.2],得到參數β不同取值導致的網絡最大連圖子圖比例變化情況如圖8所示。可以看出,網絡最大連通子圖比例變化趨勢與θ導致的最大連圖子圖比例變化情況相似,都是隨著參數的增大,網絡的抗毀性也逐漸增強,β≥0.9時,網絡發生級聯失效的概率較低,節點的失效對網絡造成的影響也較小,網絡的級聯失效抗毀性就會逐漸增強,且趨于穩定。

圖7 不同θ下的最大連圖子圖比例變化情況Fig.7 Variation of the proportion of maximum contiguous subgraphs for different values of θ

圖8 不同β下的最大連圖子圖比例變化情況Fig.8 Variation of the proportion of maximum contiguous subgraphs with different β

綜上,可以發現,容忍系數的增大可以提高網絡抵御級聯失效的抗毀性,且當容忍系數達到一定值時,網絡的抗毀性趨于穩定,級聯失效也不會對網絡的連通性造成嚴重的影響,但再繼續提高容忍參數對網絡抗毀性的提高作用不大。其次,當容量系數取較高的值時,網絡的抗毀性能便會趨于穩定,這是因為根據重要度策略攻擊的節點對網絡的連通性起著關鍵作用,這類節點最大容量的設置應使其能夠滿足節點失效后負載流的傳播,這樣網絡才能具有較強的抗毀性。此外,本文仿真分析選取的網絡具有顯著的無標度特性,即只有少量的節點擁有較大的度值,級聯失效模型的初始負載是根據節點及鄰居節點的度值所定義,且采取了與節點的初始負載成比例的重分配策略,故當網絡節點受到攻擊的過程發生級聯失效時,會有較多的負載流經度值較小的節點,而這類節點的初始負載和容量一般都相對較小,無法承接來自失效節點的高額負載,從而加劇了對網絡連通性和可達性的破壞,需要設置較大的容量參數獲取更大的節點容量,以增強網絡抵御級聯失效的能力。

分析可知:成渝鐵路網絡在面對隨機攻擊時表現出較強的抗毀性,而面對重要度攻擊時,則表現出一定的脆弱性,在關鍵節點級聯失效情況下,其脆弱性更為顯著,隨著關鍵節點的失效,網絡性能也急劇下降,失效節點達到一定數量時,網絡會被分裂成多個孤立的子網絡,網絡徹底癱瘓,因此,在制定鐵路網絡相關應急策略時,應盡量避免級聯故障現象的發生,應做好鐵路網絡關鍵站點的防護措施,在考慮經濟效益的基礎上,適當提高節點的容量,增加關鍵節點其他節點間的耦合關系,以增強節點在出現負載過載情況時向其他站點的進行負載輸送的能力。此外,發生級聯失效現象后,應嚴格控制負載向度值較少的節點轉移的流量,以防止發生承接負載的節點沒有足夠的可替代路徑疏通路徑來繼續分配負載,造成更大規模的失效情況。

4 結論

提出了基于灰色關聯法和VIKOR法的復雜網絡節點重要度評估模型,并應用于成渝地區鐵路交通網絡,能有效識別出網絡中的重要節點。考慮到網絡節點受到攻擊的同時,網絡的結構也會隨之改變,為更精準的識別出網絡實時的關鍵節點,對節點重要度評估過程做出改進,選擇根據網絡的動態演化來評估節點的重要性,即每攻擊一個節點,便重新計算當前網絡的節點重要度,實驗結果表明,采用動態的節點重要度評估過程可以有效提高識別的精確性。在此基礎上,采用一種更符合真實網絡非線性容量負載的復雜網絡級聯失效模型進行仿真分析,仿真結果進一步驗證了節點重要度動態評估模型的有效性。同時討論了初始負載控制參數及容量控制參數在重要度攻擊策略下對網絡級聯失效的影響,實驗得到以下結論。

(1)廣安和重慶是成渝鐵路網絡中最關鍵的節點;不考慮級聯失效情況時,節點的度中心性最能表示節點在靜態網絡下的重要性,而在動態網絡拓撲結構中,介數最能代表網絡節點的重要程度;考慮級聯失效情況下,綜合性的動態評估模型更能代表節點的重要性。

(2)在以節點和鄰居節點的度值定義節點的初始負載方式下,當初始負載控制參數α∈[0.1,0.3]時,網絡在抵制級聯失效時表現出一定的脆弱性;當α≥0.4時,隨著α的增大,網絡的抗毀性也逐漸增強,但當α超過某一閾值時,網絡的魯棒性趨于穩定,繼續提高α,對網絡的增強網絡魯棒性沒有明顯效果。

(3)網絡的抗毀性與容量參數取值呈正相關,增大網絡的容量參數可以增加網絡節點的容量,減小級聯失效行為對網絡的破壞程度;受網絡拓撲結構和攻擊策略的影響,取較大的容量參數時,網絡具備較強的的抗毀性。

(4)由于選取的成渝地區鐵路網絡節點數量相對較少,在分析網絡面對級聯失效的魯棒性時,網絡容易發生多級級聯失效而迅速崩潰,導致一些結果的呈現不太明顯,因此,可進一步將本文模型應用于大型網絡,以更好地反映網絡面對級聯失效時的抗毀性情況。