智能反射面輔助的無線網(wǎng)絡(luò)加權(quán)和速率優(yōu)化設(shè)計(jì)

牛和昊,林 志,王 勇,王 磊,趙青松

(1. 國防科技大學(xué) 電子對抗學(xué)院, 安徽 合肥 230037;2. 國防科技大學(xué) 電子制約技術(shù)安徽省重點(diǎn)實(shí)驗(yàn)室, 安徽 合肥 230037)

智能反射面(intelligent reflecting surface,IRS),也被稱為可重構(gòu)智能表面(reconfigurable intelligent surfaces,RIS),作為一種新興的無線通信技術(shù)受到了科研學(xué)者的廣泛關(guān)注。該技術(shù)通過在平面上集成大量的無源反射元件,智能地重置無線傳播環(huán)境,從而顯著地提升無線網(wǎng)絡(luò)的覆蓋率和頻譜效率等性能[1]。具體地說,IRS是由大量低成本、亞波長結(jié)構(gòu)和獨(dú)立可控的無源電磁反射元件集成的均勻陣列平面。其主要功能是根據(jù)通信鏈路信息,通過軟件編程的方式調(diào)整反射信號(hào)的幅度和相位,使反射信號(hào)與其他路徑的信號(hào)構(gòu)造性相加,從而增強(qiáng)接收端期望信號(hào)功率,提高通信質(zhì)量[2]。

同基于信號(hào)再生和重傳機(jī)制的有源中繼通信相比,IRS不使用任何有源發(fā)射模塊如功率放大器,而僅將接收到的信號(hào)反射,降低了功率消耗[3]。此外,有源中繼通常以半雙工模式運(yùn)行,因此其頻譜效率會(huì)低于基于全雙工模式運(yùn)行的IRS[4]。而傳統(tǒng)的全雙工中繼需要采用自干擾消除技術(shù),其實(shí)現(xiàn)成本和復(fù)雜度均高于IRS輔助網(wǎng)絡(luò)[5]。此外,與傳統(tǒng)的反向散射通信不同,IRS用于增強(qiáng)發(fā)射端與目的端之間的通信鏈接,而不是額外發(fā)送信息。因此,IRS輔助通信不需要反向散射通信中常用的自干擾消除器,節(jié)約了硬件開銷[6]。而當(dāng)直傳鏈路被高樓等建筑物遮擋導(dǎo)致該鏈路質(zhì)量很差時(shí),IRS可以通過反射鏈路為目的端提供新的通信鏈接,因而可以有效增加無線網(wǎng)絡(luò)覆蓋范圍。

當(dāng)前,已有諸多關(guān)于IRS的研究工作。例如,文獻(xiàn)[7-8]研究了點(diǎn)對點(diǎn)通信情況下基于IRS反射的波束形成設(shè)計(jì),分別實(shí)現(xiàn)了系統(tǒng)吞吐量的最大化和基站發(fā)射功率的最小化。文獻(xiàn)[9]研究了IRS輔助的無線攜能網(wǎng)絡(luò)的聯(lián)合有源和無源波束成形的優(yōu)化設(shè)計(jì)問題,驗(yàn)證了IRS可以提高無線網(wǎng)絡(luò)的頻譜效率和能量傳輸效率。同時(shí),文獻(xiàn)[10]研究了IRS離散相位結(jié)構(gòu)下的反射系數(shù)優(yōu)化設(shè)計(jì),仿真結(jié)果表明IRS離散相位在降低硬件復(fù)雜度的前提下,可獲得接近于IRS連續(xù)相位結(jié)構(gòu)的性能。

進(jìn)一步,文獻(xiàn)[11]研究了大規(guī)模多輸入多輸出(multiple-input multiple-output,MIMO)信道中基站發(fā)送預(yù)編碼和IRS反射系數(shù)的聯(lián)合優(yōu)化設(shè)計(jì)。文獻(xiàn)[12]研究了IRS輔助的下行多輸入單輸出(multiple-input single-output,MISO)網(wǎng)絡(luò)的反射系數(shù)優(yōu)化問題。文獻(xiàn)[13]研究了IRS輔助的毫米波信道的聯(lián)合發(fā)送波束成形和發(fā)射系數(shù)的設(shè)計(jì)問題。為降低信道估計(jì)開銷,文獻(xiàn)[14]提出了一種基于雙時(shí)間尺度的波束成形和發(fā)射系數(shù)的優(yōu)化方式,其中基站波束成形矢量基于瞬時(shí)信道狀態(tài)信息設(shè)計(jì),IRS反射系數(shù)基于統(tǒng)計(jì)信道狀態(tài)信息設(shè)計(jì)。另外,文獻(xiàn)[15]針對基站不能獲取理想信道狀態(tài)信息的情況,提出了一種部分反射單元關(guān)閉的設(shè)計(jì)方式,以提高系統(tǒng)魯棒性。文獻(xiàn)[16]研究了IRS輔助下上行MISO網(wǎng)絡(luò)的發(fā)送功率最小化設(shè)計(jì)問題,結(jié)果表明IRS能有效降低無線網(wǎng)絡(luò)能量消耗。上述文獻(xiàn)中的優(yōu)化算法主要有半正定優(yōu)化法[6]、連續(xù)凸近似法[7]、交替方向乘數(shù)法(alternating direction method of multipliers,ADMM)[11-13]和懲罰對偶分解(penalty dual decomposition,PDD)法[14-16]。

然而,現(xiàn)有的IRS輔助的無線網(wǎng)絡(luò)優(yōu)化問題的求解過程較為復(fù)雜,多數(shù)情況下無法得到閉式解,從而不適用于實(shí)際通信中的實(shí)時(shí)傳輸場景。因此,IRS輔助的無線網(wǎng)絡(luò)聯(lián)合優(yōu)化設(shè)計(jì)問題仍有待進(jìn)一步研究。因此,研究低計(jì)算復(fù)雜度的發(fā)送波束形成和IRS反射系數(shù)的聯(lián)合優(yōu)化設(shè)計(jì)具有重要的理論意義和現(xiàn)實(shí)價(jià)值。本文主要針對IRS輔助的下行多用戶MISO網(wǎng)絡(luò),在滿足基站發(fā)射功率限制和反射系數(shù)恒模約束的前提下,通過聯(lián)合優(yōu)化基站的發(fā)射波束形成和IRS反射系數(shù),研究系統(tǒng)的加權(quán)和速率(weighted sum rate,WSR)最大化問題。由于原優(yōu)化問題是一個(gè)具有恒模約束的非凸優(yōu)化問題,本文提出了一種基于交替優(yōu)化(alternating optimization,AO)方法和黎曼流形梯度(Riemannian manifold gradient,RMG)方法的迭代算法。此外,為進(jìn)一步降低RMG方法的計(jì)算復(fù)雜度,設(shè)計(jì)了一種智能元素塊坐標(biāo)下降(element-wise block coordinate descent,EBCD)方法。

1 系統(tǒng)模型和優(yōu)化問題

1.1 反射系數(shù)模型

本文考慮兩種反射系數(shù)模型,第一種是連續(xù)系數(shù)模型,即|θm=1。因θm的相位可取任意值,因此有:

F1={θm|θm=ejφm,φm∈[0,2π)}

(1)

第二種反射系數(shù)模型是離散系數(shù)模型,即反射系數(shù)僅取部分有限值。本文假設(shè)θm在單位圓上等間距取τ個(gè)值,因此有:

(2)

在實(shí)際應(yīng)用中,基于連續(xù)系數(shù)模型的IRS硬件實(shí)現(xiàn)較難、成本較高,因此,將離散系數(shù)模型應(yīng)用在反射元件上更為現(xiàn)實(shí)。然而,離散系數(shù)在數(shù)學(xué)上很難直接優(yōu)化,研究連續(xù)系數(shù)的優(yōu)化對離散系數(shù)的設(shè)計(jì)具有直接的指導(dǎo)意義。

1.2 系統(tǒng)模型

圖1所示的是多用戶下行MISO網(wǎng)絡(luò),該網(wǎng)絡(luò)由1個(gè)基站,1個(gè)智能反射面和K個(gè)用戶構(gòu)成,用戶集合記做{U1,…,UK}。基站配備Nt個(gè)天線,反射面配備M個(gè)反射元素,而用戶均配備單天線。基站至反射面、反射面至第k個(gè)用戶的信道分別記作G∈Nt×M,hk∈Nt×1。假設(shè)上述信道狀態(tài)信息在基站處完全可知,而基站和用戶間的直傳鏈路被高層建筑遮擋造成了嚴(yán)重衰減,可以直接忽略。

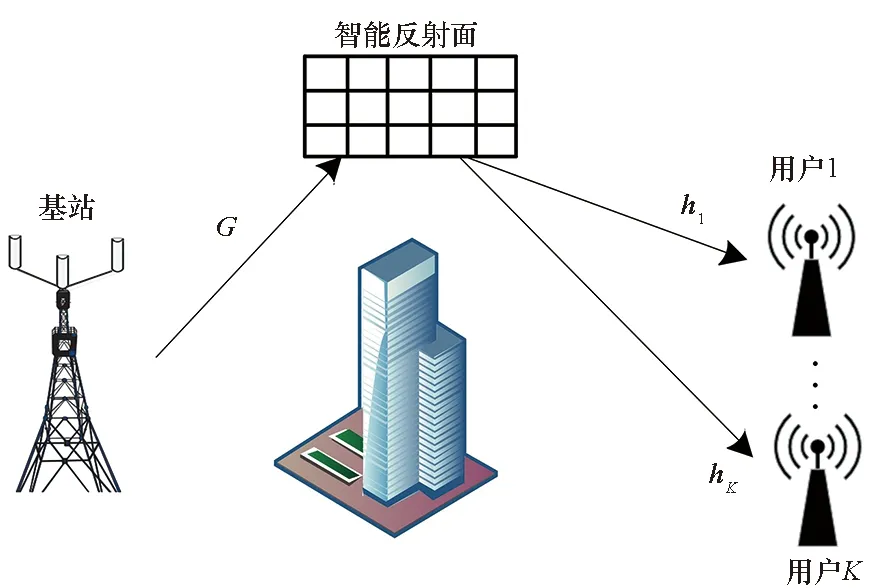
圖1 系統(tǒng)模型Fig.1 System model

因此,第k個(gè)用戶的接收信號(hào)可表示為:

(3)

由式(3)可知,第k個(gè)用戶的信干噪比(signal-to-interference-noise-ratio,SINR)為:

(4)

由式(4)可知,信道估計(jì)的復(fù)雜度與用戶數(shù)成正比,用戶數(shù)的增加造成信道估計(jì)的復(fù)雜度提高。此外,用戶數(shù)增加會(huì)造成用戶間干擾的增加,降低用戶的信息速率。

1.3 優(yōu)化問題

本文的目標(biāo)是通過聯(lián)合設(shè)計(jì)波束形成向量和反射系數(shù),最大化該網(wǎng)絡(luò)中用戶的加權(quán)和速率性能。該問題可表述為:

(5)

由于非凸目標(biāo)函數(shù)f1(F,θ)的存在,難以直接求解問題(5)。本文主要工作是設(shè)計(jì)低復(fù)雜度算法對P1進(jìn)行求解。

2 對偶交替優(yōu)化算法

2.1 拉格朗日對偶變換

為了有效處理P1中對數(shù)形式的目標(biāo)函數(shù),采用拉格朗日對偶變換方法進(jìn)行求解[17]。首先將P1等價(jià)地轉(zhuǎn)換成:

(6)

其中,α?[α1,…,αK]T,αk是對應(yīng)于γk的輔助變量。而新的目標(biāo)函數(shù)定義為:

(7)

此外,根據(jù)文獻(xiàn)[17],當(dāng)固定α?xí)r,關(guān)于{F,θ}的優(yōu)化問題可簡化為:

(8)

考慮到P1″是多個(gè)分式規(guī)劃問題(fractional programming,FP)的加權(quán)和,很難直接進(jìn)行求解。下面將采用AO方法對原問題P1″進(jìn)行迭代求解。每輪迭代中,首先更新α,接著更新{F,θ},重復(fù)該過程直到系統(tǒng)和速率性能趨于穩(wěn)定。利用式(4),P1″中的目標(biāo)函數(shù)可以寫為:

(9)

因此,當(dāng)給定α?xí)r,{F,θ}的優(yōu)化問題可寫成:

(10)

本小節(jié)引入了拉格朗日對偶變換方法將問題(5)轉(zhuǎn)換為問題(10)。下一小節(jié)中將提出一種有效的算法求解問題(10)。

2.2 交替優(yōu)化算法

根據(jù)文獻(xiàn)[18]提出的二次變換方法,f2(F,θ)可轉(zhuǎn)換為:

(11)

式中,β是引入的輔助變量,β?[β1,…,βK]T,βk∈,?k∈{1,…,K}。

由文獻(xiàn)[14]知,P2可等價(jià)表示為:

(12)

當(dāng)固定任意兩個(gè)優(yōu)化變量時(shí),f2β為關(guān)于剩余變量的凸函數(shù)。 這是因?yàn)閒2β是線性函數(shù)和二次函數(shù)的差,即該問題關(guān)于任一變量均是凸的[19]。 因此,對于f2β,可交替地求解相應(yīng)的子問題來更新變量。

此外,根據(jù)一階最優(yōu)性條件,最優(yōu)的βk為:

(13)

最優(yōu)的fk為:

(14)

式中,λ是功率約束的對偶變量,可表示為:

(15)

上式的最優(yōu)解λ*可通過二分搜索方法獲得[20]。解決P2′的關(guān)鍵在于如何求解θ。接下來,將提出兩種方法來求解問題(11)。

2.3 黎曼梯度法

首先,對于M中的任意θ,θ的切線空間表示為包含所有θ的切線向量構(gòu)成的空間,定義為:

(16)

式中,z表示θi處的切線向量。θi處的黎曼梯度gradf(θi)是一個(gè)切線向量,即歐幾里德得度在TθiM上的正交投影,由式(17)給出。

gradf(θi)=?fθi-R{?fθi⊙(θi)*}⊙θi

(17)

式中,⊙表示逐元素相乘。

因此,問題(11)的歐幾里得梯度為:

(18)

然后,將歐氏空間的優(yōu)化方法用于黎曼流形上。 根據(jù)歐氏空間中的共軛梯度下降算法,梯度的更新公式為:

(19)

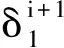
(20)

然而,式(19)中的di和di+1分布于兩個(gè)不同的切線空間TθiM和Tθi+1M中,無法直接獲得搜索方向。 針對該問題,文獻(xiàn)[22]提出一種將di映射到Tθi+1M的方法,可表示為:

Tθi→θi+1(di)?TθiM→Tθi+1M:di→

di-R{di⊙(θi+1)*}⊙θi+1

(21)

與式(19)類似,M上搜索方向的更新如式(22)所示。

(22)

最后,在獲得di后,為了保證梯度下降所獲得的點(diǎn)仍在該流形上,需要進(jìn)行回溯操作。在θi處,di的回溯定義為:

(23)

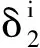
(24)

其中,round{·}表示舍入到最接近的整數(shù)。

2.4 智能元素優(yōu)化算法

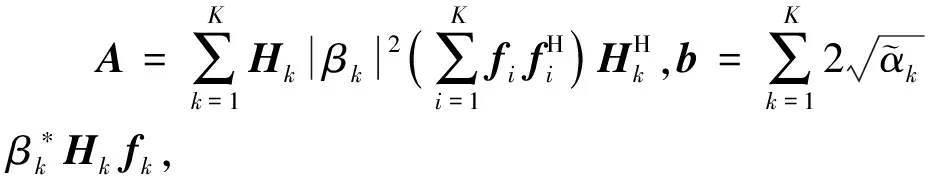
(25)

(26)

將式(25)和式(26)代入式(11)中,當(dāng)固定其余θi,i∈M,i≠m時(shí),可獲得下述關(guān)于θm的優(yōu)化問題:

s.t. |θm=1,?m∈M

(27)

因此,按照m=1到m=M的順序逐一求解問題(27),可獲得全部的反射系數(shù)。對于離散系數(shù)情況,可利用舍入運(yùn)算進(jìn)行求解,與式(24)類似,這里不再贅述。

2.5 整體算法設(shè)計(jì)

結(jié)合上述過程,本文算法主要步驟如算法1所示。

算法1 交替優(yōu)化算法

2.6 計(jì)算復(fù)雜度對比

3 仿真分析

這里對算法性能進(jìn)行仿真驗(yàn)證。仿真場景如圖2所示,包含1個(gè)基站、1個(gè)IRS、3個(gè)用戶。基站和IRS的坐標(biāo)分別為(10 m,0 m)和(0 m,50 m)。用戶假設(shè)均勻分布在一個(gè)圓內(nèi),圓心為(10 m,50 m),半徑為5 m 。此外,基站、ISR、用戶的天線高度分別為10 m、10 m、2 m。

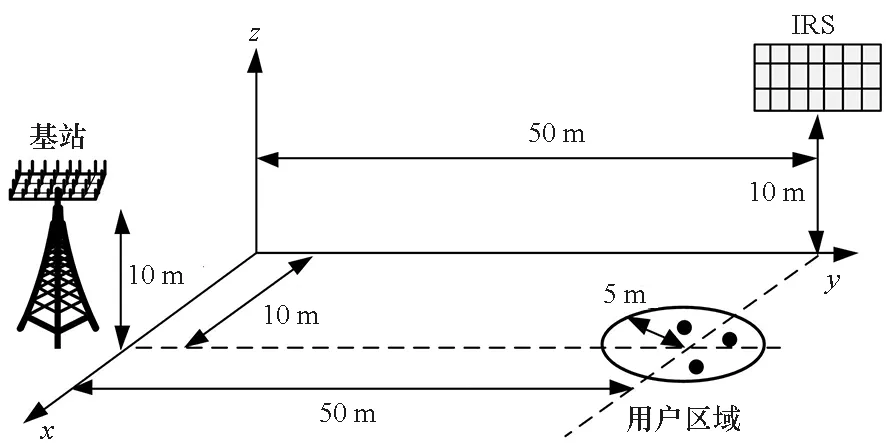
圖2 仿真場景Fig.2 Simulation scenario

首先驗(yàn)證本文算法的收斂性,其中AO算法被稱為外層迭代,而RMG或EBCD算法被稱為內(nèi)層迭代。圖3是不同M情況下RMG算法和EBCD算法的收斂性能。從圖3可以看出,兩種算法獲得的WSR性能均隨著迭代次數(shù)的增加而提升,并逐漸收斂。此外,M的增加可提升WSR。然而,M的增加會(huì)導(dǎo)致需要優(yōu)化的變量數(shù)增加,從而使收斂速度變慢。此外,在相同的條件下,EBCD算法的收斂速度比RMG算法更快。然而,相比于EBCD算法,RMG算法可以獲得更好的WSR性能。

圖3 WSR與內(nèi)層迭代次數(shù)仿真結(jié)果Fig.3 Simulation result of WSR and the iteration number of the inner layer

然后驗(yàn)證外層AO算法的收斂性。圖4給出了不同Nt和M的情況下,WSR與迭代次數(shù)的關(guān)系。與內(nèi)層迭代的結(jié)果類似,Nt或M越大,迭代次數(shù)越多。然而,對于不同的Nt或M,RMG-AO算法和EBCD-AO算法均能在很少的迭代次數(shù)時(shí)收斂。

對比圖3和圖4可看出,參數(shù)相同時(shí)內(nèi)層算法獲得的WSR比外層算法獲得的WSR低很多,原因是在內(nèi)層算法中,仿真是經(jīng)過一定次數(shù)的內(nèi)層迭代得到的{F1,θ1},以及對應(yīng)的WSR,該{F1,θ1}實(shí)際是外層優(yōu)化的起始點(diǎn)。

接下來將研究系統(tǒng)主要參數(shù)對WSR性能的影響。為了驗(yàn)證本文所提方法的優(yōu)越性,將與以下方法進(jìn)行比較:①隨機(jī)IRS方法[3],即隨機(jī)選擇反射系數(shù);②迫零(zero force,ZF)波束形成方法[5],即基于ZF準(zhǔn)則設(shè)計(jì)發(fā)射端的波束形成向量,以消除用戶之間的內(nèi)部干擾;③連續(xù)反射系數(shù)方法[10],可視作離散系數(shù)情況的性能上界;④ ADMM;⑤ PDD方法。本文方法和這幾種方法分別記作AO-RMG方法、AO-EBCD方法、隨機(jī)IRS、ZF波束形成、連續(xù)反射系數(shù)、ADMM和PDD方法。

圖5給出了WSR與基站最大發(fā)射功率Ps之間的關(guān)系,從圖中可以看出,所有方法的WSR性能均隨著Ps的增大而提升,而本文所提出的AO-RMG方法的性能非常接近連續(xù)反射系數(shù)的性能,驗(yàn)證了本文所提離散系數(shù)設(shè)計(jì)的有效性。此外,AO-RMG方法的性能和ADMM、PDD方法的性能十分接近,而AO-RMG方法的計(jì)算復(fù)雜度低于其他算法,驗(yàn)證了本文所提算法的實(shí)用性。此外,AO-EBCD方法犧牲了部分性能換來了收斂速度的加快,因此可根據(jù)實(shí)際的通信需求靈活選擇并應(yīng)用AO-RMG及AO-EBCD算法。

圖5 WSR與最大發(fā)射功率的關(guān)系Fig.5 Relationship of WSR and the maximum transmit power

圖6比較了不同方法獲得的WSR與反射單元個(gè)數(shù)的關(guān)系。從圖中可以看到,M的增大可明顯提升WSR性能。這主要有兩個(gè)原因:首先,M的增大可以提高IRS接收到的信號(hào)功率,從而獲得更高的陣列增益。其次,在合理優(yōu)化反射系數(shù)的前提下,隨著M的增大,用戶接收到的反射信號(hào)功率也隨之增大。反之,由于隨機(jī)IRS方法僅能利用陣列增益來提升WSR,性能增長較為緩慢。該結(jié)果表明,通過一定的方法優(yōu)化反射系數(shù)后,增強(qiáng)反射單元個(gè)數(shù)可以明顯提高無線網(wǎng)絡(luò)的頻譜效率。

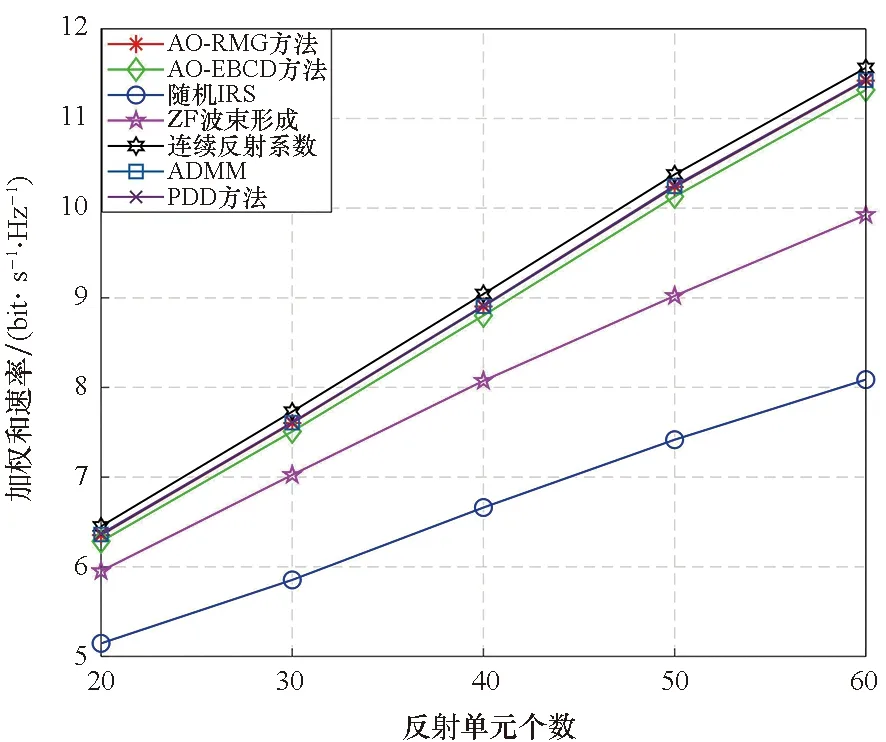
圖6 WSR與反射單元個(gè)數(shù)的關(guān)系Fig.6 Relationship of WSR and the number of elements

圖7 單用戶信息速率與權(quán)值的關(guān)系Fig.7 Relationship of single user information rate and weight

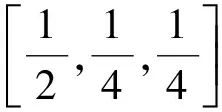
實(shí)際上,本文算法經(jīng)過適當(dāng)修改可有效解決該問題。具體,當(dāng)ωk為優(yōu)化變量時(shí),首先將ωk視作常量,即選定一組ωk的初值對其余變量進(jìn)行優(yōu)化求解,這里可直接使用本文中的方法。再求解得到其余變量后,回到式(7),將ωk視作優(yōu)化變量進(jìn)行優(yōu)化,可得到以下優(yōu)化問題:

0≤ωk≤1,?k

(28)

該問題關(guān)于ωk是凸問題,可用優(yōu)化工具包CVX求解。在得到優(yōu)化的ωk后,再利用本文算法求解其他優(yōu)化變量,然后求解上述問題得到ωk。上述過程交替迭代,可獲得優(yōu)化后的ωk和其他變量。

為驗(yàn)證上述方法的有效性,針對多用戶進(jìn)行權(quán)值分配的場景,研究了該網(wǎng)絡(luò)的加權(quán)和速率與最大發(fā)射功率的關(guān)系,這里除了權(quán)值為優(yōu)化變量外,其余設(shè)定和圖5一致。仿真結(jié)果如圖8所示。對比該圖結(jié)果和圖5可知,最優(yōu)權(quán)值分配可提升多用戶網(wǎng)絡(luò)的加權(quán)和速率性能。

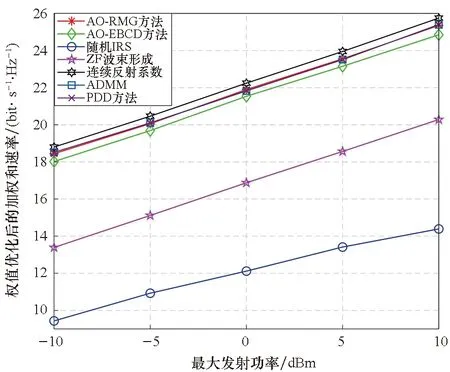
圖8 權(quán)值優(yōu)化后WSR與最大發(fā)射功率的關(guān)系Fig.8 Relationship of WSR and the maximum transmit power after weight optimization

4 結(jié)論

本文研究了IRS輔助多用戶下行網(wǎng)絡(luò)的波束形成和反射系數(shù)的聯(lián)合優(yōu)化問題,最大限度地提升系統(tǒng)用戶的加權(quán)和速率。為了求解非凸的目標(biāo)函數(shù),提出了一種AO方法,其中采用RMG方法來優(yōu)化反射系數(shù),并使用二分搜索法優(yōu)化發(fā)送波束形成向量。此外,為了降低RMG方法的復(fù)雜度,設(shè)計(jì)了一種EBCD方法。仿真結(jié)果驗(yàn)證了本文算法的有效性,與隨機(jī)反射系數(shù)等方法相比,本文所提的波束形成和反射系數(shù)聯(lián)合優(yōu)化方法能有效提高網(wǎng)絡(luò)頻譜效率,實(shí)際性能與ADMM及PDD算法非常接近。此外,通過設(shè)計(jì)不同的權(quán)值參數(shù),不同用戶實(shí)際可獲得不同的信息速率性能,因此本文算法有很強(qiáng)的靈活性和實(shí)用性。