基于π定理及多元線性回歸的河道穩定水力幾何形態公式研究

閆志方,賈云飛

(1.廣東珠榮工程設計有限公司,廣東 廣州 510610;2.廣州開發區財政投資建設項目管理中心,廣東 廣州 510000)

河道水力幾何形態指河道流量、輸沙率、河寬、水深、流速等之間的相互關系,穩定水力幾何形態即在挾沙水流長期作用下可能形成的與所在河段流量、泥沙等條件相適應某種均衡形態[1]。準確預測一定水沙條件下河道斷面的穩定水力幾何形態對河道防洪、渠道設計、河道整治、航運碼頭建設等均有重要意義。河道穩定水力幾何形態最早是由Kennedy[2]開展研究,經過大量地匯總分析印度渠道的不沖不淤資料,構建了平均水深H與平均流速U之間的經驗關系。繼Kennedy后,大量學者開始了對穩定特征變量經驗關系的研究:Lindley[3]認為穩定河道的形態取決于流量、床沙的天然特性和床沙的輸沙量以及河段的粗糙度,他對Chenab運河下游展開了廣泛勘察并收集了觀測數據,最終得到了穩定河道中穩定河寬、穩定水深、穩定比降、穩定流速之間的經驗關系式;Lacy[4-5]分析了大量可用數據并提出了3個方程,阻力方程、河寬方程、比降方程,其中河寬方程和比降方程分別建立了穩定河寬、穩定比降和造床流量的經驗關系;Leopold等[6]針對美國中西部的河流建立了穩定河道方程,他們通過觀察發現對河流的穩定特征參量可用同一頻率下流量的指數形式表示;Blench[7]應用2個分別代表河床材料和河岸材料參數,并且又引入了一個阻力方程,聯立后得出了穩定河寬、穩定水深、穩定比降與造床流量之間的顯式方程;錢海強[8]根據西北江三角洲多年實測數據,采用Leopold的水力幾何形態關系建立了北江三水河段斷面河相關系并探討了其河相特征及其變化;李倩[9]通過對國內404個實測河道斷面數據進行分析,提出了一套以流域面積和河流發育系數為標準的河流寬度計算方法。以上經驗方法得到的穩定水力幾何形態關系式看似簡單,但是其重要性是不可估量的,這些經驗方程為渠道、河道、航運等設計提供了有效的工具,在實踐中被廣泛應用。

然而,利用以上方法得到的結果,存在很大區域局限性,一般也只適用于資料來源區,前人的方法也是針對資料來源區所擬合的經驗公式。與前人得到的河道穩定水力幾何形態經驗關系式不同的是,本文基于π定理找出了影響參數,運用大量原型觀測和水槽實驗資料作為樣本數據進行線性回歸分析,提出了穩定河道水力幾何形態關系式。

1 量綱分析

本文所研究的河道水力幾何形態特征參數主要有穩定河寬、穩定水深、造床流量、床沙中值粒徑等。Yalin等[10]提出與河道穩定水力幾何形態相關的變量AR可用Q、ρ、υ、γs、D、g表示:

AR=fA(Q,ρ,υ,γs,D,g)

(1)

則穩定河寬和穩定水深可以表示為:

BR=fB(Q,ρ,υ,γs,D,g)

(2)

hR=fh(Q,ρ,υ,γs,D,g)

(3)

式中AR——河道穩定水力幾何形態變量;BR——穩定河寬,m;hR——穩定水深,m;Q——造床流量,m3/s;ρ——水流密度,kg/m3;υ——水流運動黏滯系數,m2/s;γs——床沙容重,kN/m3;D——床沙粒徑,本文中為中值粒徑,mm;g ——重力加速度,m/s2。

分別選取D、Q、γs為幾何學、運動學、動力學量,且3個量相互獨立。

應用π定理:

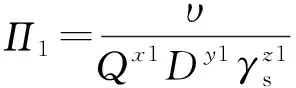
(4)

(5)

(6)

式(4)—(6)分子和分母應滿足量綱一致性,則第一個因子的量綱關系有:

[υ]=[Q]x1[D]y1[γs]z1

(7)

即 [L2T-1]=[L3T-1]x1[L]y1[ML-2T-2]z1

(8)

由式子兩邊量綱相等,得到:

[L]:2=3x1+y1-2z2

[T]:-1=-x1-2z2

[M]:0=-z2

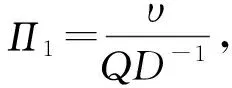
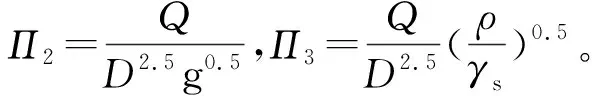
則式(2)、(3)可變為:

(9)

(10)

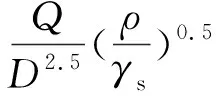
(11)

(12)

2 公式擬合

2.1 樣本數據來源

本文樣本數據來源于前人發表文獻及工程報告[11-23],數據主要涉及加拿大安大略省西南部諸河流、加拿大阿爾伯塔省諸河流、美墨邊境格蘭德河等河流。為使擬合公式更適用于天然沖積河流,本文從從原始數據中選取寬深比50.05 mm。其中包括11組原型觀測數據及2組實驗數據,見表1。

2.2 數據分析

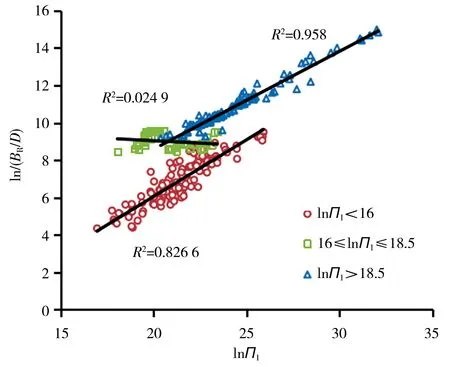
a)lnΠ1

從圖1看出,ln(BR/D)與lnΠ1、lnΠ2有較明顯的線性關系,且根據lnΠ1和lnΠ2的不同取值,ln(BR/D)～lnΠ1和ln(BR/D)～ lnΠ2顯現不同的線性關系,其關系分為3部分,其中lnΠ2<16及lnΠ2>18.5兩部分樣本點相關性顯著,R2分別為0.887和0.961,在兩部分的過渡區域16≤lnΠ2≤18.5,ln(BR/D)與lnΠ2之間相關性不明顯;ln(BR/D)～lnΠ1的關系同樣分為3部分,其中lnΠ2<16及lnΠ2>18.5兩部分樣本點相關性顯著,R2分別為0.827和0.958,同樣在兩段的過渡區域16≤lnΠ2≤18.5,ln(BR/D)與lnΠ1關系不明確。

同樣從圖2看出,ln(hR/D)與lnΠ1、lnΠ2有較明顯的線性關系,且根據lnΠ1和lnΠ2的不同取值,ln(hR/D)～lnΠ1和ln(hR/D)～ lnΠ2分別有不同的線性關系,其相關關系分為3部分,其中lnΠ2<16及lnΠ2>18.5兩部分樣本點相關性顯著,R2分別為0.865和0.932,在兩部分的過渡區域16≤lnΠ2≤18.5,ln(hR/D)與lnΠ2之間相關性不明顯;ln(hR/D)～lnΠ1的關系同樣分為3部分,其中lnΠ2<16及lnΠ2>18.5兩部分樣本點相關性顯著,R2分別為0.442和0.775,同樣在兩段的過渡區域16≤lnΠ2≤18.5,ln(hR/D)與lnΠ1關系不明確,R2僅為0.009。

圖1、2這種分段分布的特性與以往一些學者研究的到經驗公式法是不同的,并且通過這些規律本文作者進行猜想,圖中的過渡區域可能是天然沖積河流某種特征發生轉變的過渡狀態。

2.3 公式擬合

通過上文對樣本數據分析,可在線性相關顯著的區域(lnΠ2<16及lnΠ2>18.5)分別建立以ln(BR/D)、ln(hR/D)為因變量,lnΠ1和lnΠ2為自變量的二元線性回歸方程(13)和(14):

(13)

(14)

式中,aB、bB、cB、ah、bh、ch分別為待定參數,Π1、Π2含義同式(9)、(10)。

通過二元線型回歸分析求得式(13)、(14)的待定參數及相關性見表2、3。

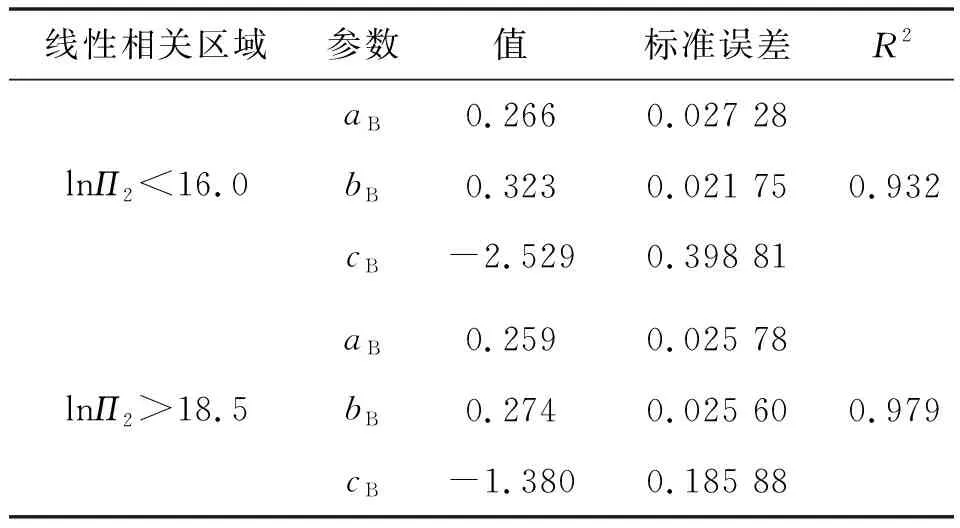
表2 式(13)待定參數值、標準誤差及R2

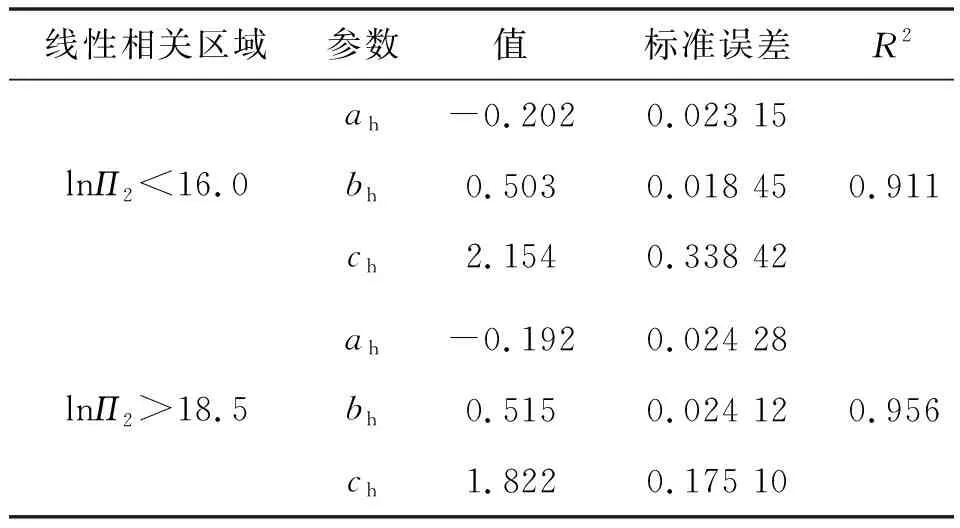
表3 式(14)待定參數值、標準誤差及R2

將表2、3中各參數代入式(13)、(14),分別得出式(15)、(16)。

(15)

(16)

分別將式(15)、(16)去對數得式(17)、(18)。

(17)

(18)

式中各符號含義見式(1)—(3)。

從式(15)—(18)看出,本文得到的關系式在16≤lnΠ2≤18.5區間關系混亂,沒有較好的表達式,這也不難聯想到雷諾數與阻力系數的關系與之類似,因此針對本文提出的經驗方法還有待深入研究,以得到具有普遍適用性的河道穩定水力幾何形態計算方法。

3 公式精度檢驗

3.1 檢驗數據

本文用于公式精度檢驗的數據來源于文獻[24-28],主要涉及河流為土庫曼斯坦Kara-Kum河、俄羅斯Saratov河、新西蘭Porter河、中國長江等河流,并且檢驗數據與用于公式擬合的樣本數據不同源(表4)。

表4 檢驗數據來源及變化范圍

3.2 公式檢驗

戴文鴻等[29]通過對3種經典的穩定河道水力幾何形態計算方法進行了分析與比選,選出了計算精度較高的Yalin和da Silva方法。故本文將采用Yalin和da Silva方法作為標準方法,分別將式(17)、(18)及Yalin和da Silva方法計算出的穩定水力幾何形態,以實測值為橫坐標,計算值為縱坐標,對計算結果進行對比,結果見圖3、4。

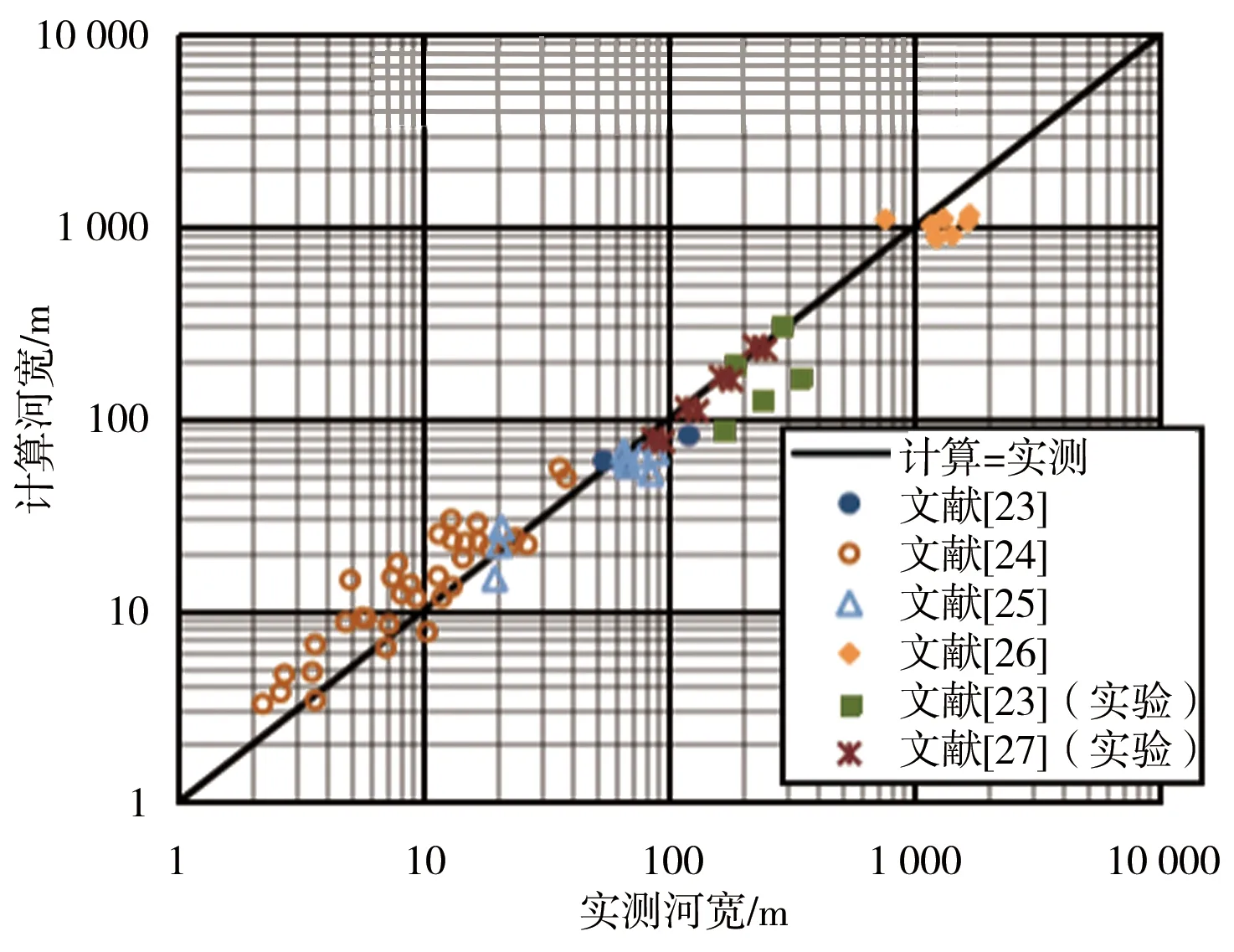
a)式(17)、(18)計算結果

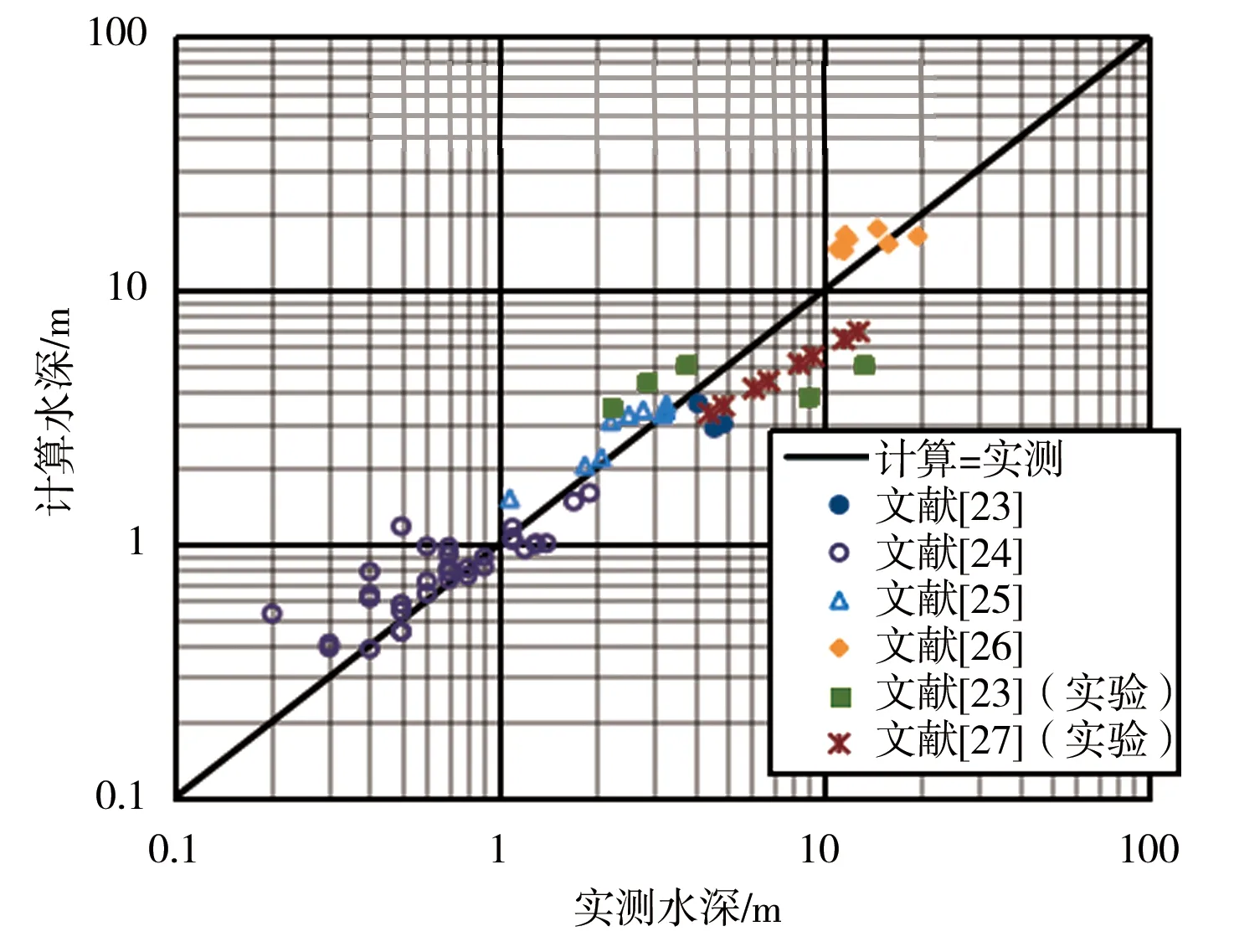
a)式(17)、(18)計算結果

由圖3可看出,對于穩定河寬計算,本文式(17)、(18)計算及Yalin和da Silva方法計算結果散點均集中且均勻分布于“計算=實測”直線兩側,表明本文計算公式與Yalin和da Silva方法計算值均與實測值接近。

由圖4可看出,對于穩定水深計算,本文式(17)、(18)計算結果散點集中且均勻分布于“計算=實測”直線兩側,表明計算值與實測值接近;而Yalin和da Silva方法對于文獻[23]的計算散點分布于“計算=實測”直線下側,說明計算值小于實測值,其余大部分散點均較均勻集中分布于直線兩側。總體而言,對于穩定水深本文計算公式與Yalin和da Silva方法計算值均與實測值接近。

以上是通過散點分布情況定性比較檢驗,為定量檢驗本文公式計算精度,需采用誤差指標進行對比。閆志方等[30]在比較溢洪道寬頂堰流量系數公式時采用了差異比(DR)、相對誤差(RE)、幾何平均偏差(GAD)3個指標,本文將采用這3項指標來分析比較計算值與觀測值之間的誤差。指標計算見式(19)—(21):

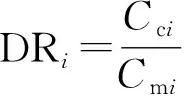
(19)

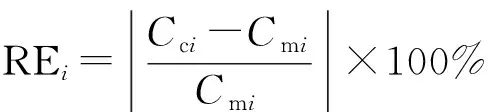
(20)

(21)

式中Cc——計算值;Cm——實測值;N——數據組數。

DR越接近1表示計算值與觀測值越接近;RE越接近0表示計算值與觀測值越接近;GAD越接近1表示計算值與觀測值越接近。

經計算,本文式(17)、(18)與Yalin和da Silva方法計算結果的平均相對誤差、平均差異比以及幾何平均偏差對比見表5。

表5 本文公式與Yalin和da Silva方法誤差指標比較

由表5誤差指標比較可得出以下結論。

a)本文公式計算河寬和水深的平均相對誤差分別為36.6%和30.3%,Yalin和da Silva方法計算河寬和水深的平均相對誤差分別為38.7%和31.4%,本文公式計算河寬和水深的平均相對誤差略低。

b)本文公式計算河寬和水深的平均差異比分別為1.18和1.09,Yalin和da Silva方法計算河寬和水深的平均相對誤差分別為1.20和1.04。對于河寬的計算,本文公式計算結果更接近于實測值,而對于水深計算Yalin和da Silva方法計算結果更接近實測值。

c)本文公式計算河寬和水深的幾何平均偏差分別為1.37和1.33,Yalin和da Silva方法計算河寬和水深的平均相對誤差分別為1.42和1.38。對于河寬和水深的計算,本文公式計算結果更接近于實測值。

綜上分析,總體而言本文公式計算結果的誤差指標略優于Yalin和da Silva方法,但從各誤差指標的數值上看2種方法差別不大,可認為2種方法計算精度相當。因此,可將本文公式應用于河道防洪、渠道設計、河道整治、航運碼頭建設等工程實踐當中。

4 結論

a)基于量綱分析理論找出了穩定河道水力幾何形態的影響參數Π1和Π2,可將穩定河寬BR和穩定水深hR分別表達為BR/D=fB(Π1,Π2)和hR/D=fh(Π1,Π2),原型觀測和水槽試驗資料作為樣本數據進行線性回歸分析,得出穩定河寬BR和穩定水深hR的表達式。

b)對比本文公式及Yalin和da Silva方法計算的河寬散點圖,2種方法計算值均與實測值接近;對比兩者計算的水深散點圖,本文公式計算值與實測值接近,而Yalin和da Silva方法少量散點計算值小于實測值,其余大部分散點均較均勻集中分布于直線兩側。總體而言,本文計算公式與Yalin和da Silva方法計算的河寬和水深值均與實測值接近。

c)對比各誤差指標,總體而言本文公式計算結果略優于Yalin和da Silva方法,但從各誤差指標的數值上看2種方法差別不大,可認為兩者計算精度相當,故可將本文公式應用于工程實踐當中。