基于高階譜估計(jì)的反輻射導(dǎo)彈抗有源誘餌研究*

朱華剛

（中國(guó)船舶集團(tuán)有限公司第七一〇研究所 宜昌 443003）

1 引言

反輻射導(dǎo)彈是壓制和摧毀雷達(dá)的最有效的武器［1］。目前，ARM 正面臨著越來(lái)越多的嚴(yán)峻挑戰(zhàn)；其中，有源誘餌誘偏已成為影響ARM 有效發(fā)揮其威力的一項(xiàng)主要的因素。因此，尋求新的技術(shù)與方法，以應(yīng)付誘餌的挑戰(zhàn)是當(dāng)前ARM 亟待解決的問(wèn)題之一。

由一部被保護(hù)雷達(dá)和一個(gè)或多個(gè)有源誘餌組成的有源誘偏系統(tǒng)，可以利用寬頻帶反輻射導(dǎo)彈導(dǎo)引頭分辨角大的特點(diǎn)加上雷達(dá)的功率管理以及誘餌設(shè)置的脈沖前沿陷阱，實(shí)現(xiàn)對(duì)反輻射導(dǎo)彈的誘偏作用［2］。由上述分析可得出：寬頻帶反輻射導(dǎo)彈抗誘餌誘偏的有效方法之一是減小導(dǎo)引頭的分辨角，在較遠(yuǎn)距離分辨出雷達(dá)與誘餌，從而依靠信號(hào)識(shí)別出雷達(dá)，并且有比較充分的時(shí)間修正失誤距離以達(dá)到攻擊雷達(dá)的目的。從這一角度出發(fā)，我們考慮在比相體制的基礎(chǔ)上，增加高階譜估計(jì)測(cè)向。誘餌可以用于非相干源，誘餌輻射源的工作頻率、發(fā)射波形、脈沖定時(shí)等與雷達(dá)發(fā)射機(jī)完全一致；同時(shí)也可采用相干源，使誘餌輻射源輻射信號(hào)與雷達(dá)輻射信號(hào)構(gòu)成一定的相位關(guān)系［3］。本文只研究誘餌為非相干源的情況。

高階空間譜估計(jì)測(cè)向技術(shù)是基于四階累積量的空間譜估計(jì)技術(shù)。算法本身繼承了傳統(tǒng)空間譜估計(jì)算法的優(yōu)質(zhì)特性，具有較高的精度和分辨率，可實(shí)現(xiàn)同時(shí)對(duì)多目標(biāo)進(jìn)行測(cè)向。與二階算法相比具有有效擴(kuò)展陣列孔徑［4］和抑制高斯噪聲的優(yōu)勢(shì)［5］。綜合上述優(yōu)越性，在反輻射導(dǎo)引頭上采用該項(xiàng)技術(shù)可以分辨時(shí)域、頻域重疊的目標(biāo)和誘餌信號(hào)，從而為反輻射導(dǎo)彈抗誘餌干擾提供了前提保證。

MUSIC算法應(yīng)用于均勻圓陣測(cè)向，在進(jìn)行譜峰搜索時(shí)需要在二維全平面內(nèi)搜索，加之四階累積量矩陣本身構(gòu)造繁重，導(dǎo)致了四階MUSIC 算法的運(yùn)算量大大增加。本文采用了模式空間激勵(lì)的方法可將陣元空間內(nèi)的均勻圓陣轉(zhuǎn)化為模式空間內(nèi)的虛擬均勻線(xiàn)陣，從而通過(guò)降低譜峰搜索的維數(shù)，減少四階MUSIC算法的計(jì)算量。

2 四階MUSIC測(cè)向原理

四階MUSIC 算法的主要思想是利用四階累積量代替二階MUSIC算法中的二階統(tǒng)計(jì)量。

假設(shè)M 元均勻圓陣，接收到空間D個(gè)遠(yuǎn)場(chǎng)窄帶平面波信號(hào)，則t時(shí)刻陣列接收信號(hào)可表示為

式中，A=[a(θ1'φ1)'a(θ2'φ2)'...'a(θD'φD)]為方向矢量矩陣，第i個(gè)信號(hào)對(duì)應(yīng)的方向矢量為

S(t)=[s1(t)'s2(t)'...'sD(t)]T為信號(hào)矢量，N(t)=[n1(t)'n2(t)'...'nM(t)]T為噪聲矢量。

在非高斯信號(hào)和高斯噪聲的假設(shè)下，信號(hào)與噪聲之間獨(dú)立，陣列接收數(shù)據(jù)的四階累積量矩陣為

式中：

C4x的第(k1-1)M+k3行、(k2-1)M+k4（1 ≤k1'k2'k3'k4≤M）列元素為

需要強(qiáng)調(diào)的是：對(duì)于高斯噪聲，無(wú)論是白噪聲還是譜特性未知的色噪聲，理論上噪聲的四階累積量矩陣C4n應(yīng)恒為0 矩陣，C4x中己經(jīng)抑制了高斯噪聲的影響。但由于噪聲偏離高斯分布或有限數(shù)據(jù)長(zhǎng)度運(yùn)算精度的原因，實(shí)際中C4n是不恒為0的小量矩陣［6］。

得到陣列接收信號(hào)的四階協(xié)方差矩陣后，對(duì)其進(jìn)行特征分解，由特征值大小分布判定信號(hào)個(gè)數(shù)D，較大的D 個(gè)特征值對(duì)應(yīng)的特征向量張成四階信號(hào)子空間Es=[u1'u2'...'uD]。而其余M2-D 個(gè)較小的特征值對(duì)應(yīng)特征向量張成四階噪聲子空間EN=[uD+1'uD+2'..'uM2]。

理想情況下四階信號(hào)子空間的方向矢量b(θi'φi)=a(θi'φi)?a*(θi'φi)'(i=1'...'D) 和四階噪聲子空間正交，定義四階MUSIC空間譜：

再利用類(lèi)似二階方法的譜峰搜索得到四階空間譜的峰值位置即可以估計(jì)出信號(hào)方向。

3 基于模式空間的四階改進(jìn)算法

對(duì)于均勻圓陣測(cè)向，四階MUSIC 算法的計(jì)算量主要集中在二維譜峰搜索這一環(huán)節(jié)。因此降低運(yùn)算量的重點(diǎn)在于譜峰搜索的化簡(jiǎn)。模式空間算法［7］，即利用空間預(yù)處理技術(shù)將陣元空間內(nèi)的均勻圓陣變換成相位模式空間內(nèi)的虛擬均勻線(xiàn)陣。模式空間法與四階MUSIC 算法相結(jié)合，僅利用一維搜索就可以得到四階相應(yīng)的譜函數(shù)，從而減少了算法的計(jì)算量。

圖1 均勻圓陣的陣列結(jié)構(gòu)模型

3.1 圓陣的模式空間

沿圓陣饋人的激勵(lì)為E(?)時(shí)，形成的遠(yuǎn)場(chǎng)方向圖為［8］

式中，Jk(·)為k 階第一類(lèi)Bessel 函數(shù)，為簡(jiǎn)便我們省略常數(shù)ck。令β=2πr/λ，則總的遠(yuǎn)場(chǎng)方向圖為

離散均勻圓陣可以看作連續(xù)圓陣經(jīng)采樣后獲得。因此M元離散均勻圓陣的激勵(lì)為

s(?)為關(guān)于圓陣陣元角度?的采樣函數(shù)：

可做傅立葉分解：

對(duì)于構(gòu)成E(?) 的任一復(fù)指數(shù)分量Ek(?)=exp(jk?)，有

可得對(duì)應(yīng)某一分量的遠(yuǎn)場(chǎng)方向圖：

當(dāng)取M＞2K 時(shí)，忽略延拓項(xiàng)后對(duì)應(yīng)于某一分量的遠(yuǎn)場(chǎng)方向圖近似為

3.2 模式空間虛擬均勻線(xiàn)陣的構(gòu)成

若對(duì)均勻圓陣的陣列接收數(shù)據(jù)作如下變換：

其中：

下面給出四階模式空間處理的主要步驟：

1）由式（19）構(gòu)造矩陣J；2）由式（20）、（21）構(gòu)造矩陣F；3）通過(guò)式（18）得到模式空間變換矩陣T；4）通過(guò)變換矩陣T 得到模式空間中的數(shù)據(jù)矩陣，然后按四階MUSIC 算法求其四階協(xié)方差矩陣，進(jìn)行特征分解，計(jì)算譜函數(shù)并進(jìn)行一維搜索就可以估計(jì)信號(hào)源的方向。

可以推出，真實(shí)均勻線(xiàn)陣只有180°的測(cè)向范圍，而虛擬均勻線(xiàn)陣的測(cè)向范圍擴(kuò)大到（-180°，180°］，實(shí)際對(duì)應(yīng)著均勻圓陣的方位角（0°，360］。虛擬均勻線(xiàn)陣在其測(cè)向全空間內(nèi)具有相同的分辨力。

4 仿真結(jié)果及分析

4.1 高斯色噪聲條件下二階和四階算法測(cè)向比較

四個(gè)獨(dú)立2PSK 信號(hào)分別從（250°，15°）、（100°，25°）、（200°，50°）、（80°，80°）入射到7 元均勻圓陣，半徑10cm，信號(hào)頻率2GHz，采樣點(diǎn)數(shù)4000，信噪比0dB，二階、四階MUSIC 算法估計(jì)結(jié)果分別如圖2、3所示。

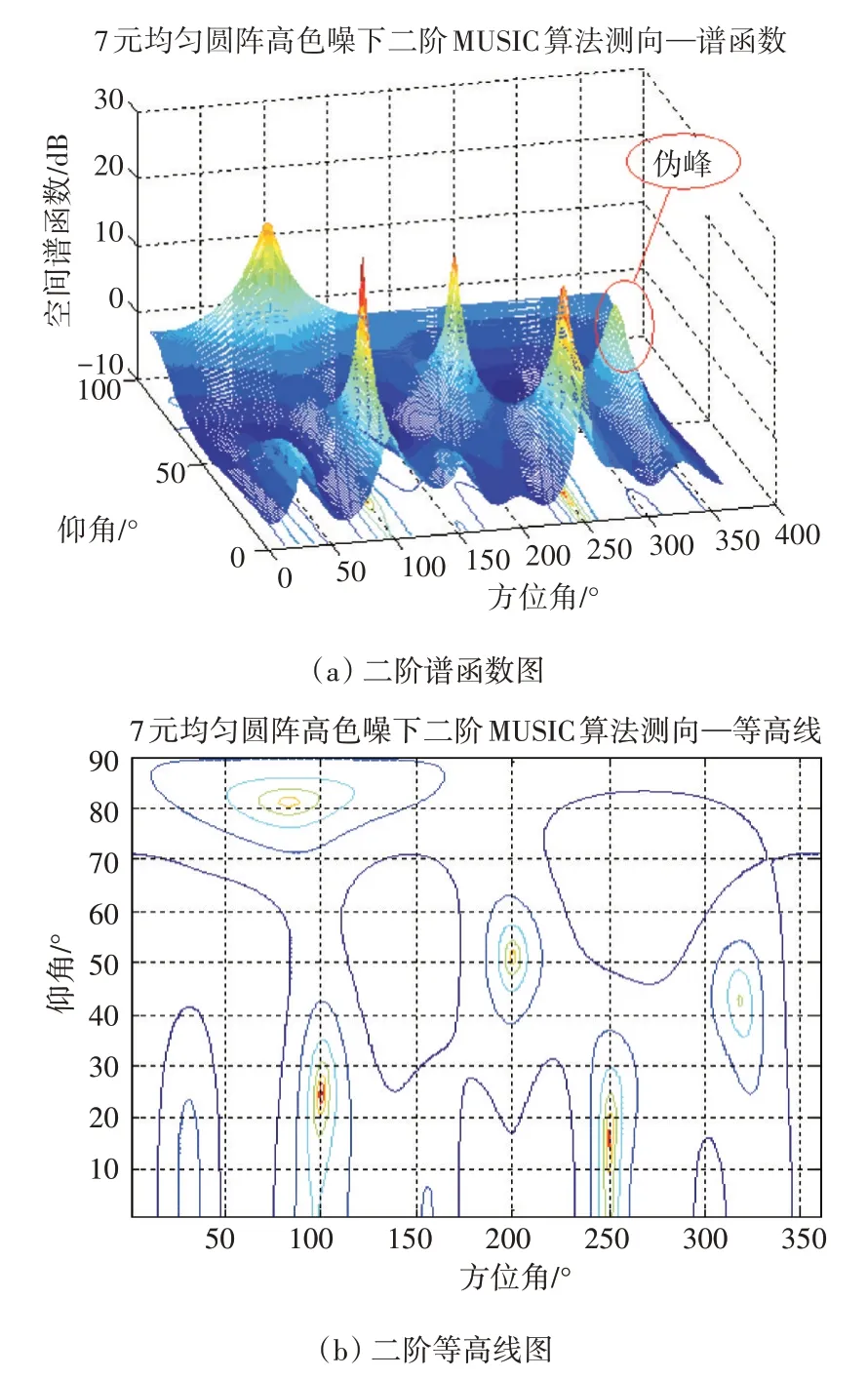
圖2 二階MUSIC測(cè)向結(jié)果

圖3 四階MUSIC測(cè)向結(jié)果

由圖2、3 可以看出，低信噪比情況下二階MUSIC 測(cè)向受到高斯色噪聲的影響，在仰角43°、方位角320°處產(chǎn)生了偽峰，并且個(gè)別角度的估計(jì)值存在偏差；而四階算法仍能保持較高的準(zhǔn)確度。

表1 高斯色噪聲條件下7元UCA利用MUSIC算法測(cè)向結(jié)果

4.2 陣列擴(kuò)展

六個(gè)獨(dú)立的2FSK 信號(hào)分別從（30°，10°）、（50°，20°）、（80°，35°）、（110°，50°）、（150°，65°）、（180°，80°）入射到5 元均勻圓陣，半徑5cm，信號(hào)頻率3GHz，采樣點(diǎn)數(shù)2000，高斯白噪聲，信噪比為20dB，四階估計(jì)結(jié)果如圖4所示。

圖4 五元均勻圓陣測(cè)六個(gè)信號(hào)

4.3 基于模式空間的四階MUSIC改進(jìn)算法

四個(gè)獨(dú)立的2PSK 信號(hào)分別從方位角100°、120°、223°、243°入射到半徑為10cm 的9 元均勻圓陣，信號(hào)頻率1.5GHz，采樣點(diǎn)數(shù)1000，高斯白噪聲，信噪比20dB，最大模式3，原始四階算法和改進(jìn)算法估計(jì)結(jié)果如圖5。

圖5 四階算法和基于模式空間的改進(jìn)算法測(cè)向結(jié)果

背景噪聲為高斯白噪聲，信噪比20dB 時(shí)，均勻圓陣在不同陣元數(shù)、不同采樣點(diǎn)數(shù)和不同信源數(shù)的情況下測(cè)向，基于模式空間變換的四階MUSIC 算法改進(jìn)前后的Matlab 運(yùn)行時(shí)間比較見(jiàn)表2。可以看到，基于模式空間的改進(jìn)算法可以有效降低運(yùn)算時(shí)間，采樣點(diǎn)數(shù)越多，效果越明顯。

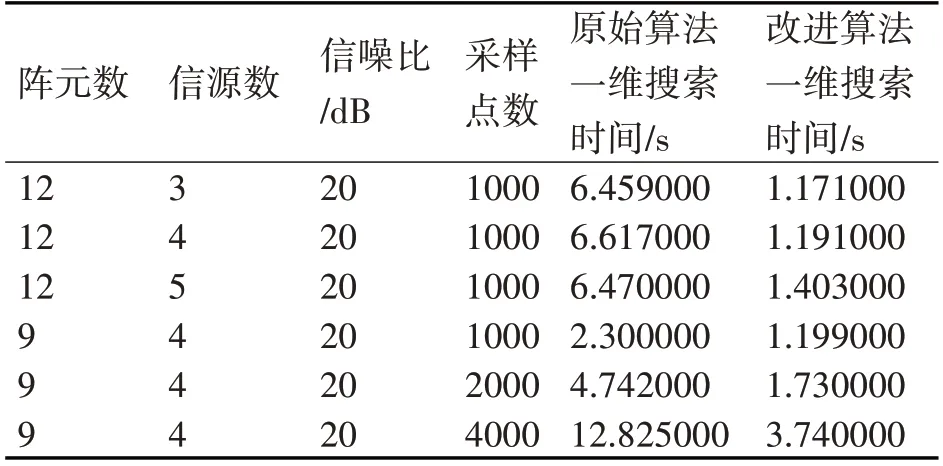
表2 基于模式空間的改進(jìn)算法測(cè)向的Matlab運(yùn)算時(shí)間

改進(jìn)算法在高斯色噪聲為背景，不同信噪比情況下利用半徑10cm 的9 元均勻圓陣對(duì)四個(gè)獨(dú)立信號(hào)測(cè)向，每個(gè)信噪比情況進(jìn)行100 次獨(dú)立試驗(yàn)，估計(jì)結(jié)果的均方根誤差見(jiàn)圖6。

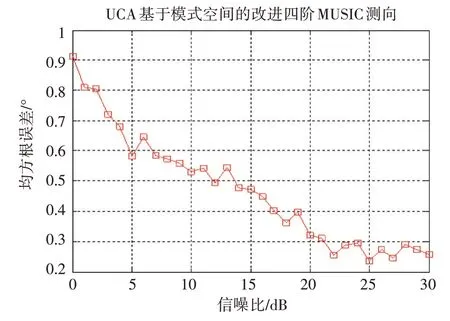
圖6 不同信噪比下改進(jìn)算法的估計(jì)性能

利用模式空間將均勻圓陣轉(zhuǎn)換為虛擬均勻線(xiàn)陣，由此可以得到的虛擬均勻線(xiàn)陣具有平移不變性。信源角度相差的越大，根據(jù)改進(jìn)算法得到的譜峰越尖銳。由圖6 可以看到，隨著信噪比的增加，改進(jìn)算法的估計(jì)精度會(huì)變高。

5 結(jié)語(yǔ)

本文將相位模式激勵(lì)方法與四階MUSIC 算法相結(jié)合，將譜峰搜索由二維簡(jiǎn)化到一維，有效降低了均勻圓陣四階算法的計(jì)算量，通過(guò)仿真驗(yàn)證了該方法的有效性，并且驗(yàn)證了四階累積量的陣列擴(kuò)展性質(zhì)及其對(duì)高斯色噪聲的有效抑制。研究結(jié)果表明，基于四階累積量的MUSIC 算法應(yīng)用于反輻射導(dǎo)彈對(duì)雷達(dá)及誘餌的測(cè)向，具有其可行性和有效性，為反輻射導(dǎo)彈抗有源誘餌提供了前提保障。