基于優化算法的波浪能裝置最大輸出功率設計

王驥源，賀冠翔，趙書玲

（江西理工大學電氣工程與自動化學院，江西 贛州 341000）

波浪能是一種重要的海洋可再生能源，分布廣泛，儲量豐富，具有可觀的應用前景，如何將波浪能最大化地轉化利用成為新能源領域的熱門話題。波浪能轉換裝置有液壓式、氣壓式、機械式3 種形式，李燕等[1]研究表明，液壓式波浪能轉換裝置由于轉換效率高、輸出穩定，為首選波浪能轉換裝置。液壓式裝置又可細分為點頭鴨式、搖擺式、閥式、振浮式4 種，其中振浮式應用研究最廣，振浮式波浪能裝置主要通過垂蕩和縱搖獲取并轉換波浪能[2]。對于此類裝置輸出功率的優化，國內做了不少研究，已有的相關研究中，研究人員通常借助軟件仿真、算法優化等方式找出相應的最大輸出功率。潘海鵬等[3]基于遺傳算法對以浮子為驅動裝置的直驅式海浪發電系統的最大功率進行跟蹤控制，此方法可大幅度提升發電系統對波浪能的捕獲效率；黃俊豪等[4]借助WFT 法獲取波浪能發電系統最大功率的捕獲條件，并結合Simulink 仿真，最終提升了使得系統功率輸出的優化效果；楊俊華等[5]根據商用軟件求解浮子的非線性參數，結合改進型的鯨魚算法，優化了相應負載參數，進而提高了波浪能捕獲效率。

本文根據振浮式波浪能轉換裝置垂蕩和縱搖這2 種運動方式，并建立該裝置運動和功率模型，在此基礎上進行數值求解和算法優化，設計出了實現波浪能裝置輸出功率最大化的最優系統參數，為實際應用提供參考。

1 問題的提出及理論依據

圖1 為振浮式波浪能裝置示意圖，由浮子、振子、中軸及能量輸出系統（簡稱“PTO 系統”，包括彈簧、直線阻尼器、扭轉彈簧、旋轉阻尼器和轉軸）等構成。在波浪激勵力和波浪激勵力矩作用下，浮子同時進行垂蕩和縱搖，并通過PTO 系統使振子沿著中軸進行垂蕩和縱搖。除此之外，浮子在線性周期微幅波作用下[6]，還受到附加慣性力和附加慣性力矩、興波阻尼力和興波阻尼力矩、靜水恢復力和靜水恢復力矩的影響。振子沿中軸垂蕩時，直線阻尼器的阻尼力與浮子和振子的相對速度成正比，比例系數為直線阻尼器的直線阻尼系數；振子沿中軸縱搖時，旋轉阻尼器的扭矩與浮子和振子的相對角速度成正比，比例系數為旋轉阻尼器的旋轉阻尼系數，2 個阻尼系數在[0，100 000]區間取值。浮子和振子通過相對垂蕩運動和相對縱搖運動驅動直線阻尼器和旋轉阻尼器做功，并將所做的功作為該波浪能裝置的能量輸出。結合相關條件，計算出波浪能裝置輸出的最大功率，并確定該功率下直線阻尼器的阻尼系數和旋轉阻尼器的阻尼系數。分析問題時，考慮海水是無粘無旋的，忽略中軸、PTO 的質量和各種摩擦。

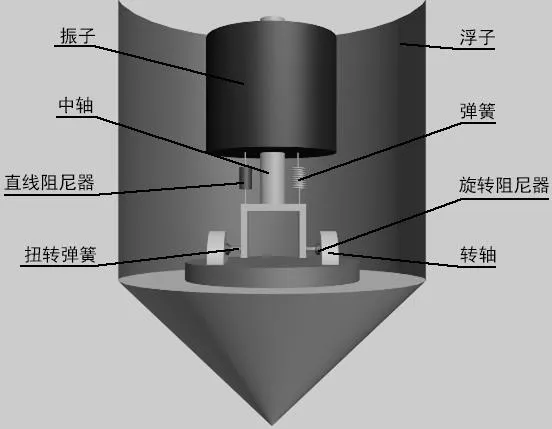
圖1 振浮式波浪能裝置示意圖

遺傳算法最早由美國的JOHO 于20 世紀70 年代提出，該算法起源于對生物系統所進行的計算機模擬研究，是一種通過模擬自然進化過程搜索最優解的方法。該算法通過數學的方式，利用計算機仿真運算將問題的求解過程轉換成生物進化中染色體基因的交叉、變異等過程。它的大致實現過程為從任意初始種群出發，通過隨機選擇、交叉和變異操作[7]，產生一群更適合環境的個體，使群體進化到搜索空間中越來越好的區域，這樣多代繁衍進化，最后收斂到一群最適應環境的個體，求得問題最優解。

2 數值模型

2.1 垂蕩運動狀態分析

裝置受力情況如下。

振子進行垂蕩時，只受PTO 系統力，而PTO 系統力包含彈簧力和直線阻尼力，具體受力情況如圖2 所示。

圖2 振子受力圖

振子的受力方程如下：

式中：F1為振子所受合力的數值；FPTO為PTO 系統力的數值；Fc為彈簧力的數值；Fx為旋轉阻尼器的阻尼力的數值。

結合上文可知，浮子受力情況如圖3 所示。

圖3 浮子受力圖

波浪激勵力可表示為：

式中：f為波浪激勵力振幅的數值；ω為入射波浪頻率的數值。

結合浮子的受力情況，并根據牛頓第二定律，可以列出浮子的垂蕩運動方程為：

式中：mb為浮子質量的數值；m′為垂蕩附加質量的數值；為浮子垂蕩運動加速度的數值；Fb為興波阻尼力的數值；Fl為靜水恢復力的數值。

同理，振子的垂蕩運動方程為：

式中：Cz為直線阻尼系數；為浮子垂蕩運動速度的數值；為振子垂蕩運動速度的數值；Kc為彈簧剛度的數值；xb（t）為浮子垂蕩位移的數值；xv（t）為振子垂蕩位移的數值。

2.2 縱搖運動狀態分析

裝置所受力矩如下。

類比垂蕩，振子進行縱搖時，受到的力矩如下：

式中：M1為振子所受力矩的數值；MPTO為PTO 系統力矩的數值；Mc為彈簧扭矩的數值；Mx為旋轉阻尼器的阻尼扭矩的數值。

結合上文可知浮子受到的力矩，并根據剛性力學中的轉動定律，可以列出浮子的縱搖運動方程為：

式中：Ib為浮子轉動慣量的數值；I′ 為縱搖附加轉動慣量的數值；為浮子角加速度的數值；Mw為興波阻尼力矩的數值；Mj為靜水恢復力矩的數值。

振子的縱搖運動方程為：

式中：Iv為振子轉動慣量的數值；為振子角加速度的數值；Kx為旋轉彈簧剛度的數值；θb（t）為浮子角位移的數值；θv（t）為振子角位移的數值；Cx為旋轉阻尼系數的數值；為浮子角速度的數值；為振子角速度的數值。

2.3 波浪能輸出功率

該裝置垂蕩時，由直線阻尼器和彈簧組成的PTO系統對外做功，因為該裝置并非是受到恒力運動，結合微元法和積分法，給出相應的功率公式如下：

該裝置縱搖時，由旋轉阻尼器和扭轉彈簧組成的PTO 系統對外做功，該裝置縱搖時受到的力矩亦非平衡，同理，輸出功率公式如下：

結合式（1）和式（2）可知，該裝置對外輸出的總功率如下：

3 數值計算和結果分析

3.1 轉動慣量的確定

在求解最大功率前，為確定裝置縱搖運動對應的常量參數，需先求出浮子和振子的轉動慣量，求解過程如下。

先建立浮子的直角坐標系，如圖4 所示。

再確定浮子質心。分別確定圓柱和圓錐對應質心坐標Z1和Z2，結合質心運動定理，可得浮子的質心坐標：

然后確定浮子面密度：

式中：ρb為浮子面密度的數值；mb為浮子質量的數值；L圓柱為圓柱半徑的數值；L圓錐為圓錐半徑的數值。

圓柱側面和圓錐側面轉動慣量計算如下：

式中：I1為圓柱側面轉動慣量的數值；I2為圓錐側面轉動慣量的數值。

最后，結合平行軸定理[8]，可求得圓柱側面和圓錐側面對于質心軸的轉動慣量之和，即浮子的轉動慣量，公式如下：

式中：d1為圓柱質心到浮子質心距離的數值；d2為圓柱質心到浮子質心距離的數值。

同理，可求得振子轉動慣量：

3.2 最大輸出功率的計算

求得轉動慣量后，結合浮子振子的運動模型和輸出功率的模型，引入波浪能裝置的常量參數（如表1所示）和直線阻尼系數、旋轉阻尼系數這2 個變量參數，編寫優化算法，求解該波浪能裝置的最大輸出功率。

表1 波浪能裝置的常量參數

算法步驟如下：①給出求解浮子振子運動狀態的算法框架1。將浮子和振子垂蕩和縱搖2 個運動對應的微分方程模型導入Matlab 的ode45 函數中，設定浮子和振子的初始位移和速度均為0，運動總時間為184.2 s，步長為0.2 s，最終可求得浮子和振子各自在0～184.2 s 內每隔0.2 s 的速度，由于尚未代入變量值，暫時無法求解。②在框架1 的基礎上，結合式（3）和式（4），先離散化計算每隔0.2 s 波浪能裝置對外所做的功，再通過數值積分計算出0～184.2 s 所做出的總功，并除以總周期，最終給出求解輸出功率所需要的算法框架2。③設定GA 工具箱的初始參數，具體設定為lb=[0，0]，表示2 個變量下限；ub=[100 000，100 000]，表示2 個變量上限；PopulationSize=10，表示種群數量；Tolfun=1e-3，表示允許誤差；CrossoverFraction=0.75，表示交叉率；EliteCount=2，表示每次遺傳中的篩選個數；Generation=20，表示迭代遺傳次數。④將步驟②中編寫好的算法框架2 導入設置好參數的GA 工具箱，并開始運行，最終求得結果。

3.3 結果分析

GA 收斂圖如圖5 所示。根據圖5 可以看到GA 算法的收斂效果較好。

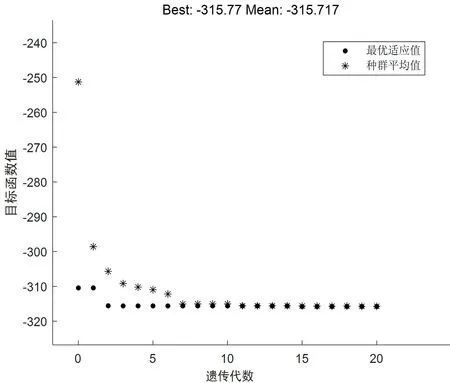
圖5 GA 收斂圖

波浪能裝置輸出的最大功率最終收斂于315.77 W，相應的最優直線阻尼系數為589 00 s/m，最優旋轉阻尼系數為95 541 s/m。

為了驗證結果的可行性，以時間為自變量、位移為因變量，給出浮子振子在最優直線阻尼系數下的垂蕩運動狀態圖，如圖6 所示。

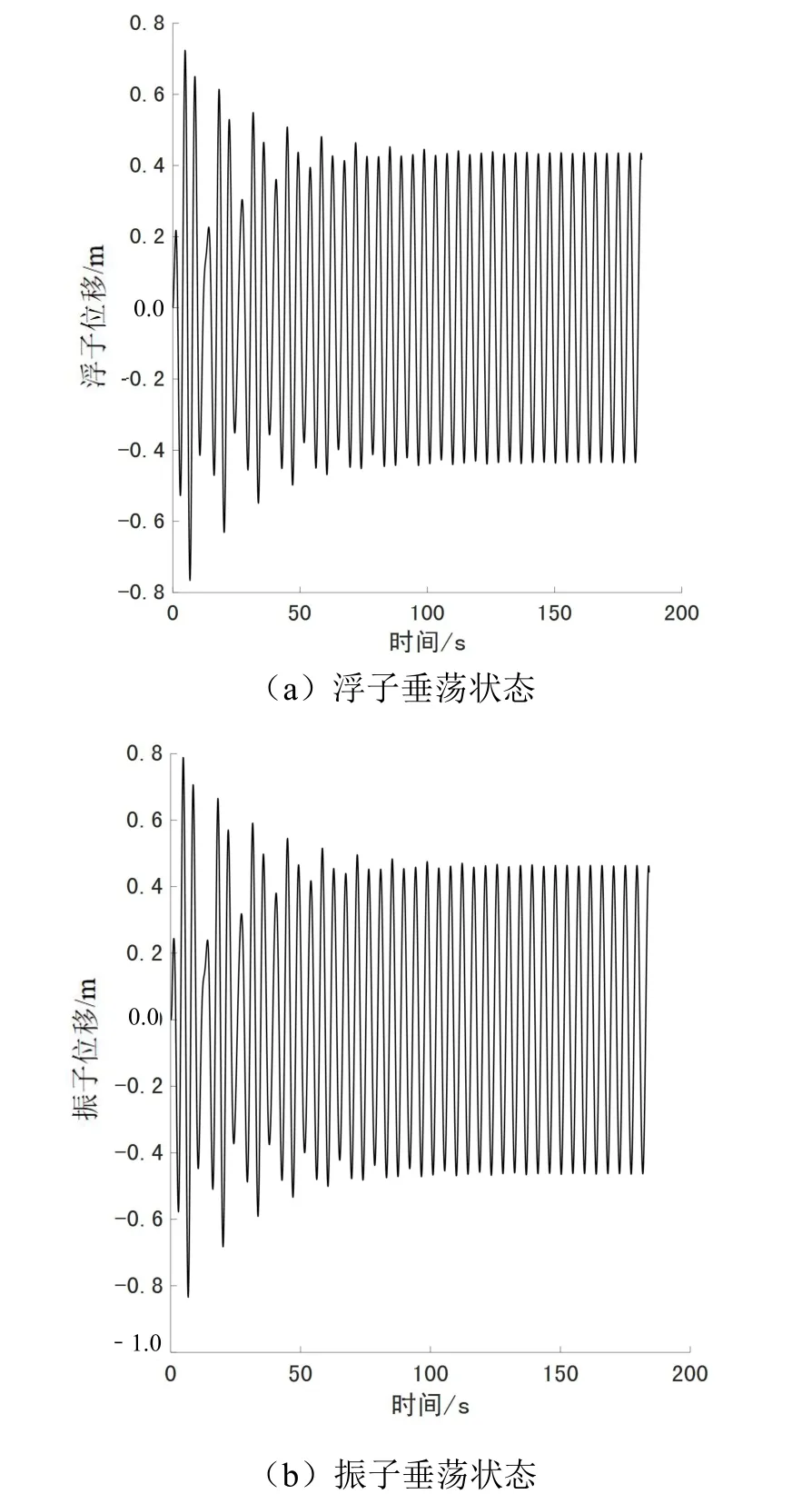
圖6 垂蕩運動圖

由圖6 不難看出浮子和振子垂蕩狀態類似波浪進行簡諧運動的狀態。除了垂蕩，再以時間為自變量、角位移為因變量，給出浮子振子在最優旋轉阻尼系數下的縱搖狀態圖，如圖7 所示。

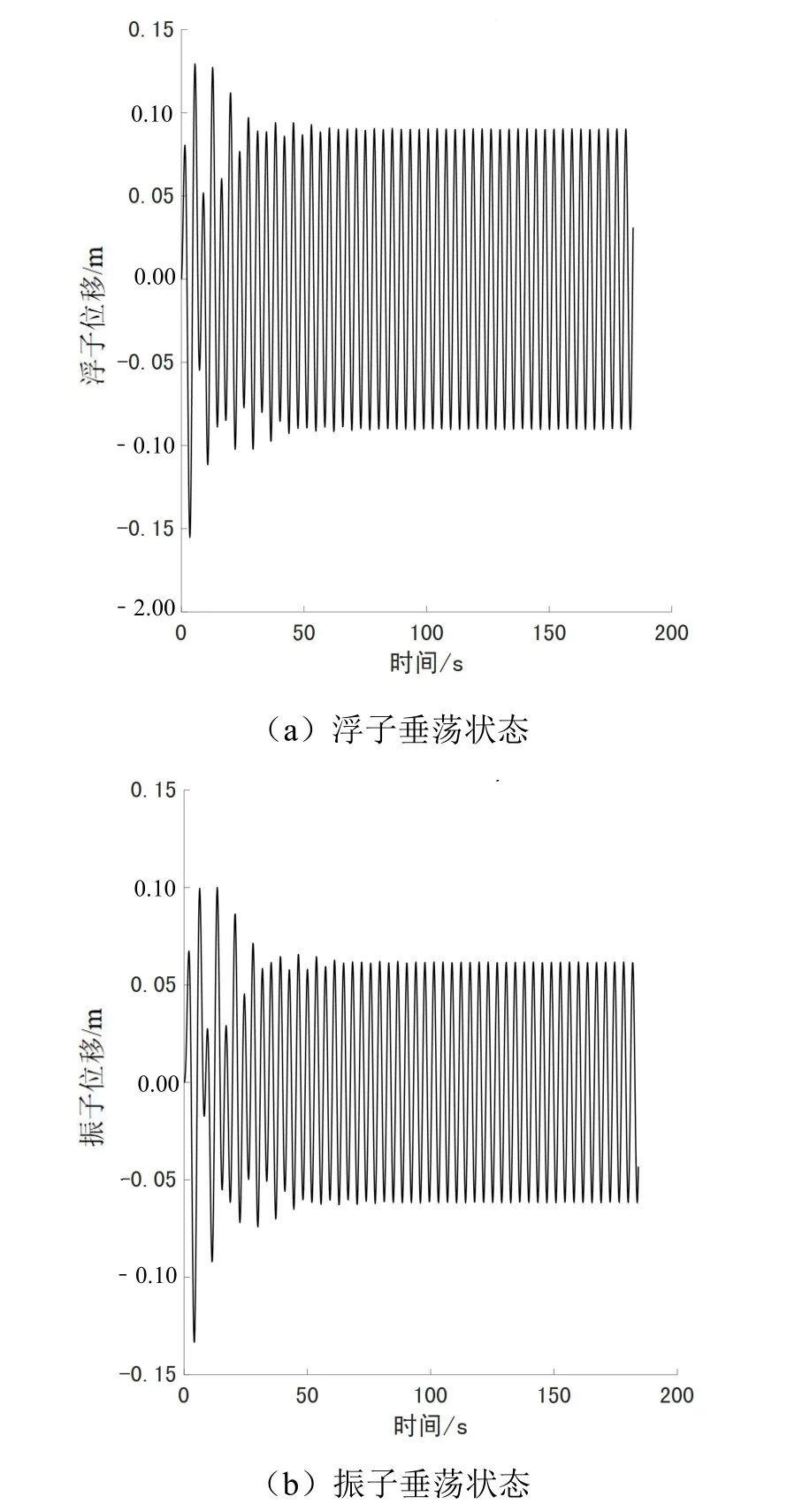
圖7 縱搖運動圖

縱搖運動也類似波浪的簡諧運動。結合遺傳算法收斂圖和裝置運動狀態圖，最終可以較好地驗證該最優系統參數的可行性，并與實際情況相符合。

4 結束語

本研究結合運動學和能量轉換等理論建立振浮式波浪能裝置輸出功率的數學模型，利用Matlab 編寫智能優化算法，對實現裝置輸出功率最大化的最優變量參數進行搜索。經Matlab 的可視化檢驗，最終得出切合實際情況的最大輸出功率和2 個最優阻尼系數，為實際推廣應用提供一定參考。

但此研究仍有不足之處，如在實際情況中，波高與風力的影響不能忽略不計，尤其是在縱搖過程中，風力矩帶來的影響不可忽略。其次，垂蕩與縱搖具有強耦合性，即垂蕩必然伴隨著縱搖，發生縱搖的同時一定會發生垂蕩。本文并未分析垂蕩縱搖的強耦合性對運動的影響，所以在今后研究中有待進一步改進。