探索不唯一的奧秘
2023-12-13 16:43:42孫宇祺
數學大王·中高年級 2023年12期
孫宇祺
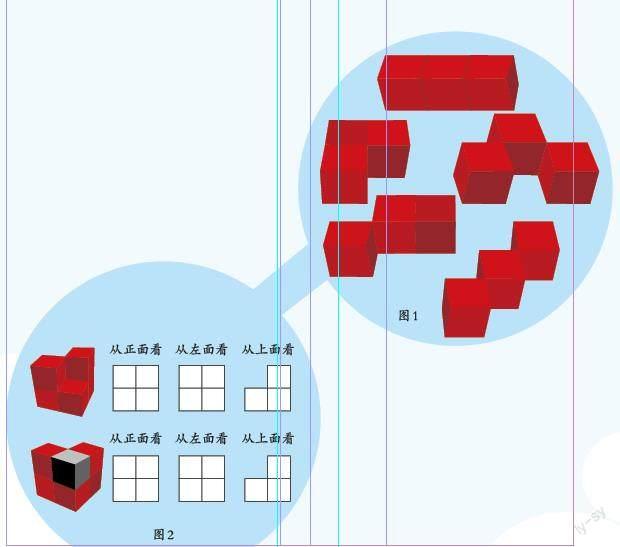
數學老師告訴我們,根據三視圖擺出原來的幾何體,一般情況下擺出的幾何體是唯一的。于是我就想:哪些情況下擺出的幾何體會不唯一?為什么會不唯一?
我決定通過擺幾何體、畫三視圖、找例子分析來尋求答案。我先思考第一個問題,從我最熟悉的小正方體開始研究,從擺一個小正方體到多個小正方體,并觀察它們的三視圖。我發現,從三個方向觀察一個小正方體,看到的三個面都是相同的;觀察兩個小正方體拼成的不同長方體,旋轉后其實是同一種幾何體。而三個小正方體的擺法有五種(如圖1),但是沒有發現三視圖相同的情況。
當我擺到六個小正方體組合時,發現擺法多達幾十種,同時也第一次出現了其三視圖和五個小正方體組合的三視圖相同的情況(如圖2)。隨著小正方體個數的增加,三視圖相同的情況越來越多。
在組合的過程中,我發現俯視圖只能反映某一位置有沒有小正方體,正視圖與每列的最高層數有關,左視圖與每行的最高層數有關。
如圖3,如果拿掉上方的黑色小正方體,這個幾何體的三視圖還是和原來一樣,因為這個黑色小正方體的位置低于同行同列的最高層。同樣,在這位置上增加一個小正方體,也不會改變這個幾何體的三視圖。
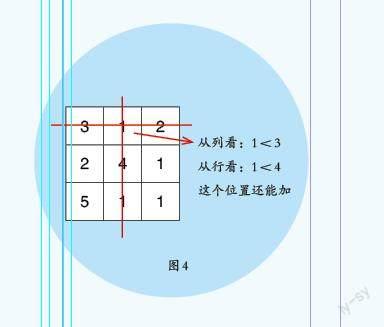
通過驗證,我發現在部分位置增加或減少小正方體而三視圖不變的情況下,最高層數都不變,這就是三視圖相同而幾何體不唯一的原因。同時,我也總結出:把三視圖轉化為“俯視標數圖”后(如圖4),只要存在某個位置比同行同列最高層數小的情況,那幾何體就不唯一。
原來,三視圖并不是萬能的。有時候三視圖相同,擺出的幾何體形狀并不唯一。也就是說,三視圖不一定能確定一個物體的形狀。數學是一門嚴謹的學科,只能說三視圖“通常”能確定一個物體的形狀,也就是老師所說的“一般情況下”。
312000浙江省紹興市上虞區博文小學 503班
指導老師? ? 林勝男

