跨座式單軌車軌耦合系統振動信號采集頻率分析

韓建棒, 申彥利,2,3*, 劉煥舉

(1.河北工程大學土木工程學院, 邯鄲 056038; 2. 河北省裝配式結構技術創新中心, 邯鄲 056038;3. 河北工程大學新型單軌交通體系工程研究中心, 邯鄲 056038)

對于跨座式單軌車軌耦合系統中,常于軌道梁跨中底部和車體重心位置放置振動加速度傳感器采集數據,經處理得到軌道梁跨中振動加速度和行車平穩性指標值來反映軌道梁與車輛的振動響應。實際的車軌耦合振動信號具有連續、隨機且頻率分布廣的特點,實際信號的奈奎斯特頻率無法確定,而通過振動加速度傳感器采集得到的是實際信號抽取得的離散信號[1]。采集頻率低會使大量實際高頻信號混入低頻信號造成信號混疊以及達不到幅值精度要求而導致測量誤差,采集信號過大則會增大計算時長,占用計算資源。因此,對跨座式單軌車軌耦合系統振動信號采集頻率分析得出合適的采集頻率范圍具有重要的學術和工程價值。

在《機車車輛動力學性能評定及試驗鑒定規范》(GB/T 5599—2019)[2]中規定,用于評價行車舒適度的鐵道機車車輛振動加速度傳感器工作頻率需為0～100 Hz。劉漢夫[3]對鐵路橋梁的橫向動力響應的測試進行分析,提出橫向加速度信號采集與分析的若干問題,認為鐵路橋梁橫向加速度信號的采集應保證信號不混疊和有效頻段加速度的幅值精度。對大跨徑高鐵橋梁動力響應信號的采集,在工程上常采用所關注最高階頻率的10倍作為采集頻率,且先用較高采樣頻率對信號進行偵測[4]。在跨座式單軌車軌耦合系統振動信號采集與處理中,常參考鐵路相關規范與研究成果。試驗者在跨座式單軌車軌耦合系統振動信號采集中,車輛與軌道梁信號常用采集頻率范圍分別為50～100 Hz和1～10 kHz[5-8],理論上來說,采樣頻率越高,采樣信號越接近于真實信號,但同時也會增加計算時長,占用計算資源。對大多跨座式軌道梁所關注的最高階頻率在5～20 Hz[9-10],若參考工程常用方法,采樣頻率偏低使采集數據達不到幅值精度、發生信號混疊,使采樣數據經處理后的結果可信度降低;而偵測選用的“較高頻率”沒有給出大致范圍,使偵測頻率的選取有一定的難度。跨座式軌道梁多采用鋼筋混凝土梁,截面形式與跨度差別較小,車橋耦合振動響應真實信號的頻率范圍相似,對單軌車輛與軌道梁振動響應信號采集頻率范圍的探究具有重要學術與工程價值。

現利用有限元軟件建立跨座式單軌車軌耦合系統,在不同車速工況下設置多組采樣頻率對車輛與軌道梁進行振動信號采集,將采集數據經處理得出的車輛與軌道梁振動響應結果進行分析,探究減少信號混疊、滿足幅值精度要求的跨座式單軌車軌耦合系統振動信號采集頻率范圍,以期為跨座式單軌車軌耦合振動響應信號采集頻率的選取提供參考依據。

1 跨座式單軌車軌耦合系統模型

1.1 車輛與輪軌接觸模型

研究采用跨座式寬輪距單軌車輛,因該車型的相關參數的測試數據較少,且與重慶跨座式單軌車輛型式相近,故根據車輛測試數據及借鑒相關車型來取用單軌車輛參數[11-14],車輛系統關鍵參數如表1所示。

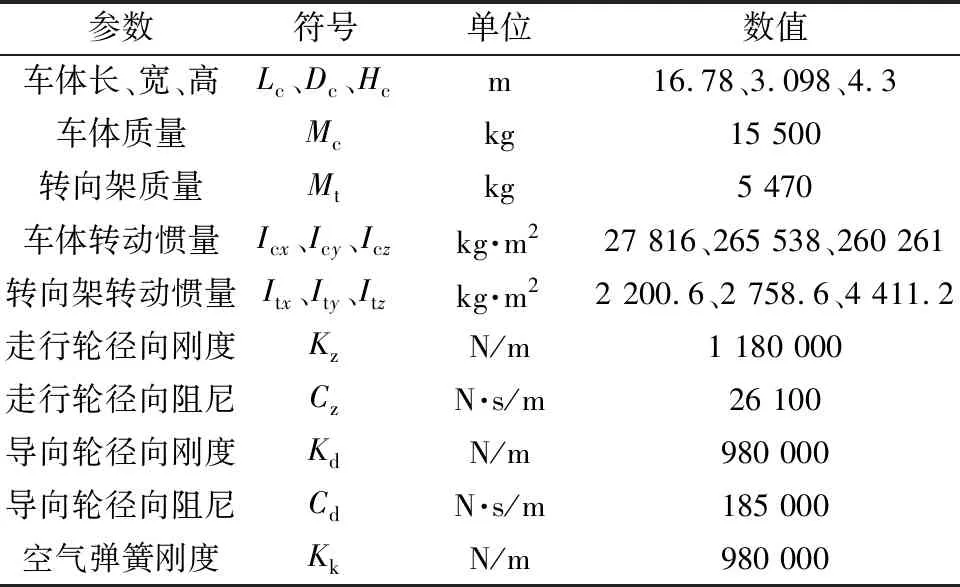
表1 單軌車輛參數Table 1 Monorail vehicle parameters

將車輛離散為車體和轉向架等剛體部件,每個部件考慮搖頭、側滾、橫擺、沉浮、點頭5個自由度,即單節共計15個自由度。在模型建立中對力學元件進行簡化,將空氣彈簧和減震器看作彈簧阻尼連接,車輛各部件對稱設置。車輛運行時沿軌道梁保持輪軌始終接觸的勻速行駛,不考慮電機振動對車軌耦合系統振動響應的影響。單軌車輛空間模型如圖1所示。

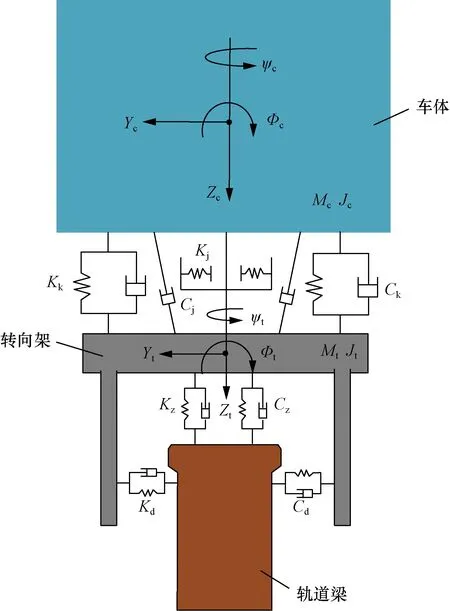
Ψc、Φc、Yc、Zc、Ψt、Φt、Yt、Zt分別為車體及轉向架的搖頭、側滾、橫擺、沉浮自由度;Kk、Ck、Kj、Cj分別為空氣彈簧和減震器的剛度與阻尼圖1 單軌車輛空間模型Fig.1 Space model of monorail vehicle

由車輛動力學理論得出單軌車輛振動平衡方程為

(1)

式(1)中:v為下標,指單軌車輛;b為下標,指軌道梁;M、C、K分別為車輛模型的質量、阻尼及剛度矩陣;Z為單軌車輛振動位移向量;Fvg為單軌車輛自身荷載向量;Fvb為軌道梁對單軌車輛作用力列向量。

單軌車輛輪胎力學特性復雜,一般情況下,當輪胎胎壓一定時,輪胎荷載與其發生的微小變形可近似為呈線性相關,故對單軌車輛充氣式橡膠輪胎的模擬可簡化為通過剛度與阻尼恒定且各向相同的彈簧連接器與轉向架并聯,即采用“線性化點接觸式”輪胎模型[15-17],如圖2所示。

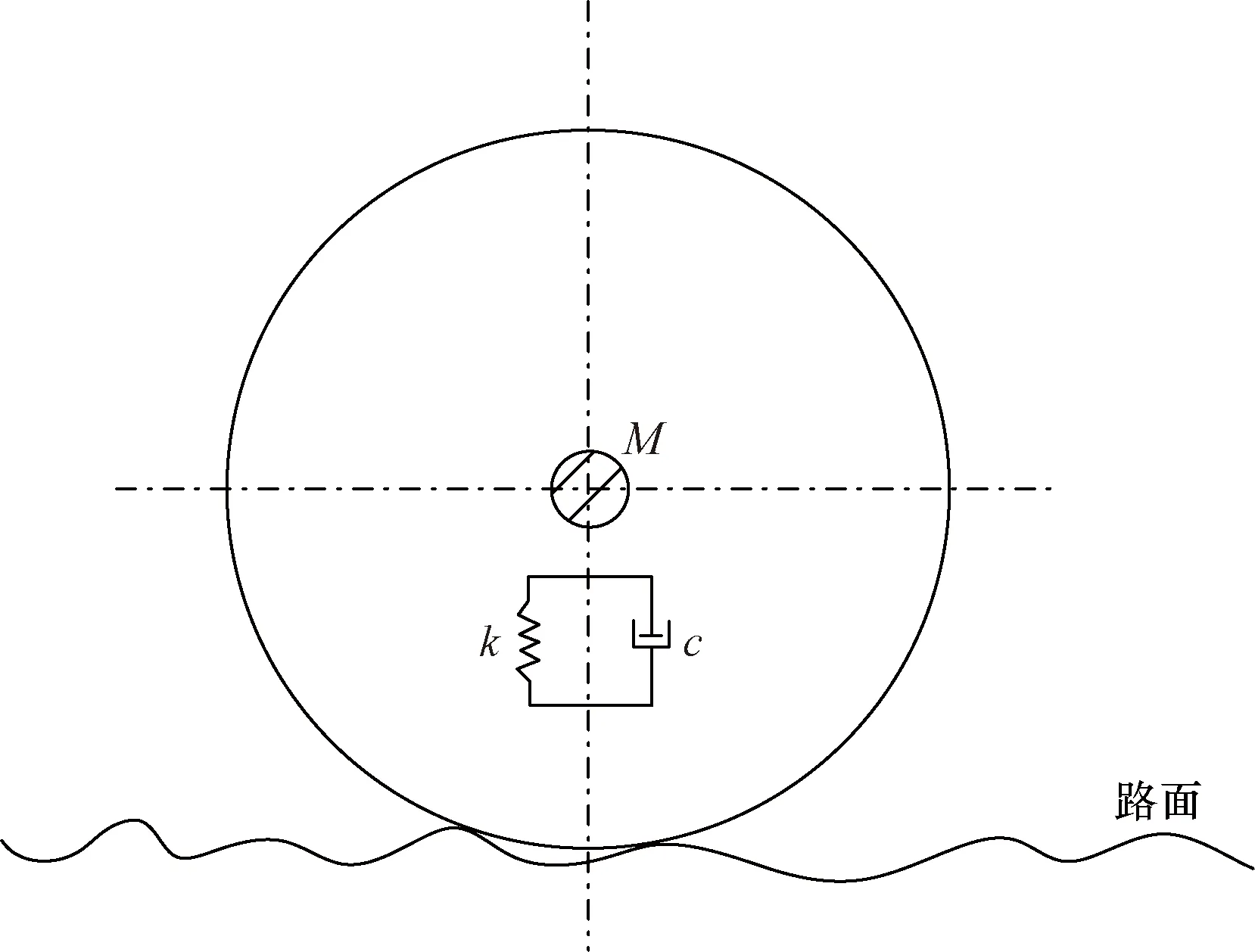
M為輪胎質量;k、c分別為輪胎徑向剛度和阻尼圖2 “點接觸式”輪胎模型Fig.2 Point contact tire model

跨座式單軌的輪胎和軌道梁接觸與公路車輛與路面接觸相似,故橡膠輪胎與軌道梁接觸的順橋向和橫橋向摩擦因數均取0.25,法向接觸根據Hertz接觸理論[18],將其看作圓柱體與彈性半空間體的接觸。

(2)

式(2)中:F為輪軌接觸力;E為路面材料彈性模量;μ為路面材料泊松比;L為輪軌接觸寬度;d為輪胎壓入深度;p0為輪軌間最大壓應力;R為橡膠輪胎半徑。

通過輪軌接觸力計算得到輪軌間最大壓應力和對應的橡膠輪胎壓入深度,將兩個參數輸入有限元分析軟件作為輪軌間相互作用接觸條件,利用輪胎與軌道梁的相互接觸來交換信息和傳遞數據以實現車橋耦合。

1.2 軌道梁與路面不平度模型

試驗采用的軌道梁為跨座式單軌交通系統常用的計算跨徑25 m的等截面混凝土簡支梁,支座設置寬度為0.8 m。為適用于跨座式寬輪距單軌車輛,軌道梁頂部寬度為1.25 m,底部寬1.1 m。為簡化計算,將軌道梁按照毛截面慣性矩進行截面換算,混凝土泊松比為0.2,彈性模量取3.96×104MPa,密度為2.55×103kg/m3,阻尼比設為0.015,軌道梁截面圖如圖3所示。

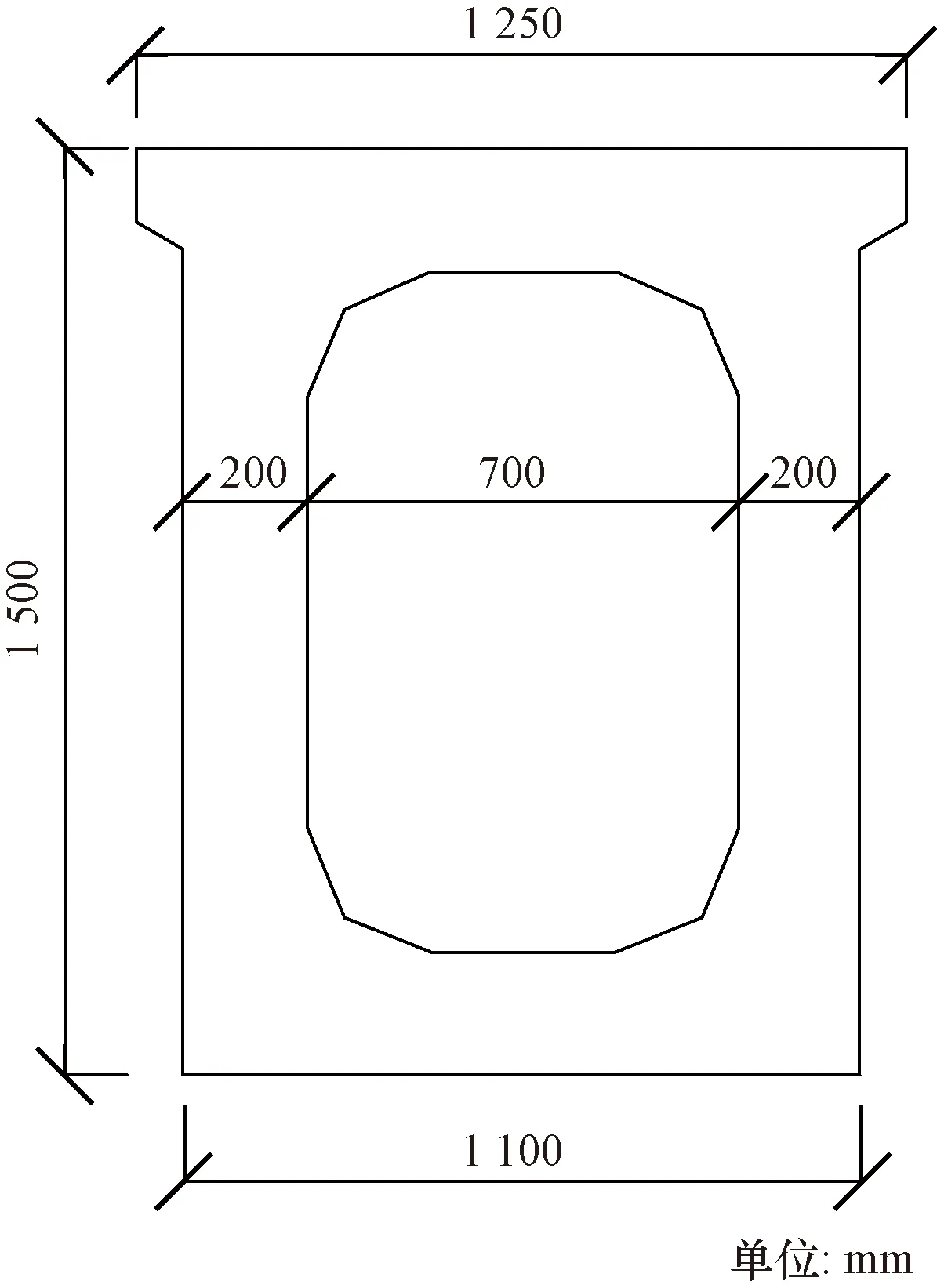
圖3 軌道梁截面圖Fig.3 Section of track beam

通過有限元法以中性軸算法進行網格劃分,將軌道梁離散化處理,每節點具有6個自由度,得到軌道梁振動平衡方程為

(3)

式(3)中;M、C、K為軌道梁模型的質量、阻尼及剛度矩陣;Z為軌道梁振動位移向量;Fbv為單軌車輛對軌道梁作用力列向量。

將車輛振動平衡方程與軌道梁振動平衡方程聯立分析知,同一工況下,即車速相同時,車輛及軌道梁質量、阻尼、剛度矩陣始終不變,則振動位移及作用力列向量也保持不變,即在該工況下車軌耦合振動響應不變。在此次求解中車輛與軌道梁時程曲線的真實信號一定,可通過設置多組不同信號采樣頻率,得到減少信號混疊、具有一定幅值精度且縮短計算時長、節省計算資源的采樣頻率范圍。

車橋耦合系統振動的激勵主要來自路面不平度的激勵。考慮到當前無適用于跨座式單軌交通系統的路面不平度譜,且單軌車輛通過橡膠輪胎在軌道梁上的行駛更接近于公路車輛在路面上行駛,故選用公路路面不平度作為軌道梁對單軌車輛在運行中的路面不平度激勵。根據《機械振動 道路路面譜測量數據報告》(GB/T 7031—2005)[19]規定,采用空間功率譜密度函數表達式作為路面不平度的模擬標準,表達式為

(4)

式(4)中:Gd(n0)為路面不平度系數,m3;n為空間頻率,m-1;n0為空間參考頻率,0.1 m-1;ω為頻率指數,取值2。

根據式(4)與文獻[20]進行MATLAB程序編寫,將路面看作由多條頻率與波長均不相同的正弦波相互疊加而成,通過傅里葉變換將眾多正弦波疊加并轉換為路面不平度高程坐標,將各個路面不平度高程坐標值導入軌道梁模型。考慮到軌道梁多采用工廠預制,對軌道梁制造環節的誤差控制較為嚴格,故試驗軌道梁走行面及導向面的路面不平度均采用A級路面。路面不平度函數曲線圖如圖4所示。

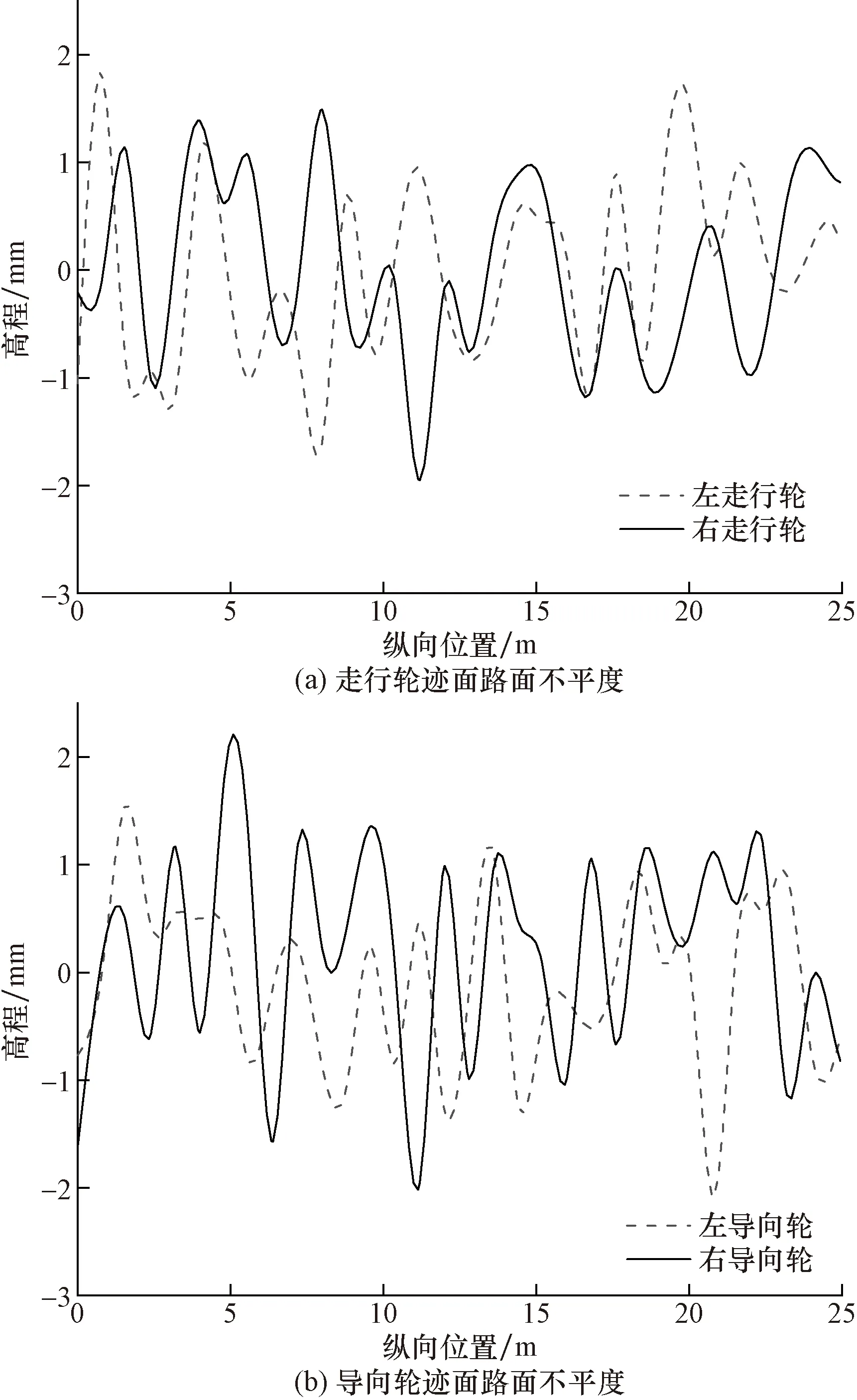
圖4 路面不平度函數圖Fig.4 Graph of road roughness function

2 車軌耦合系統振動響應結果分析

采用車輛行車平穩性來反映車輛振動響應,根據《機車車輛動力學性能評定及試驗鑒定規范》(GB 5599—2019)規定及相關文獻[21],將車輛振動時程曲線按頻率分組,計算每組的行車平穩性指標Wi,根據每組車輛平穩性指標Wi計算整個時程曲線的行車平穩性指標W,公式如下。

(5)

(6)

式中:Wi為第i組頻率對應的行車平穩性指標值;A為車體振動加速度,m/s2;f為車體振動加速度頻率,Hz;F(f)為頻率修正系數;n為整個時程曲線按頻率分組總數。

將計算得到的車輛行車平穩性指標值根據規范要求的行車平穩性評定等級進行評價,行車平穩性評定等級如表2所示。

表2 行車平穩性評定等級Table 2 Ride stability rating grade

由采樣得車輛自上橋到出橋過程的軌道梁跨中振動時程曲線,經40 Hz低通濾波得到跨中振動加速度最大值來反映軌道梁動力響應。

2.1 信號采集頻率對車輛響應的影響

車輛振動信號的采集點置于車體重心,設置車速v為30、60、90 km/h共3種工況,車輛有輪胎及減震器、空氣彈簧等一系懸掛用于減振,因此車輛振動信號采集頻率探究范圍選用20～800 Hz。通過數據采集,得到3種工況下各信號采集頻率的車輛振動時程曲線,圖5即車速60 km/h時,信號采集頻率為20 Hz和200 Hz下的車輛振動加速度時程曲線對比圖。觀察對比圖可知,采樣頻率200 Hz比20 Hz的時程曲線能夠捕捉更多樣本,使車體振動時程曲線能更準確地表達。

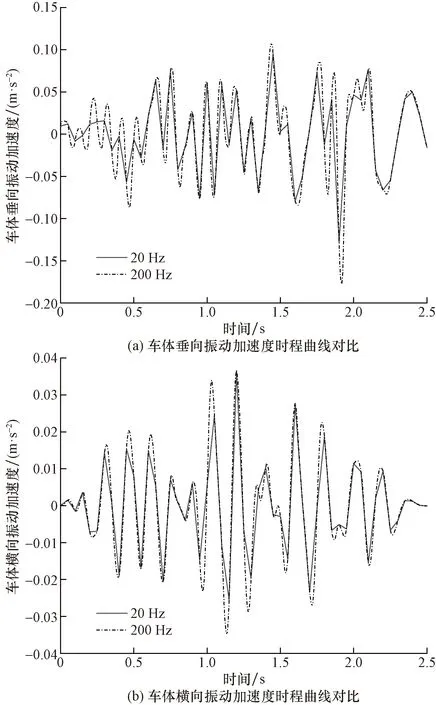
圖5 20 Hz和200 Hz采樣頻率下的車體振動加速度時程曲線對比Fig.5 Comparison of vehicle body vibration acceleration time history curves at the sampling frequency of 20 Hz and 200 Hz

將車輛振動時程曲線進行頻率分組,根據式(5)、式(6)計算得行車平穩性指標,得到不同車速下車輛振動響應隨信號采集頻率變化的趨勢如圖6所示。

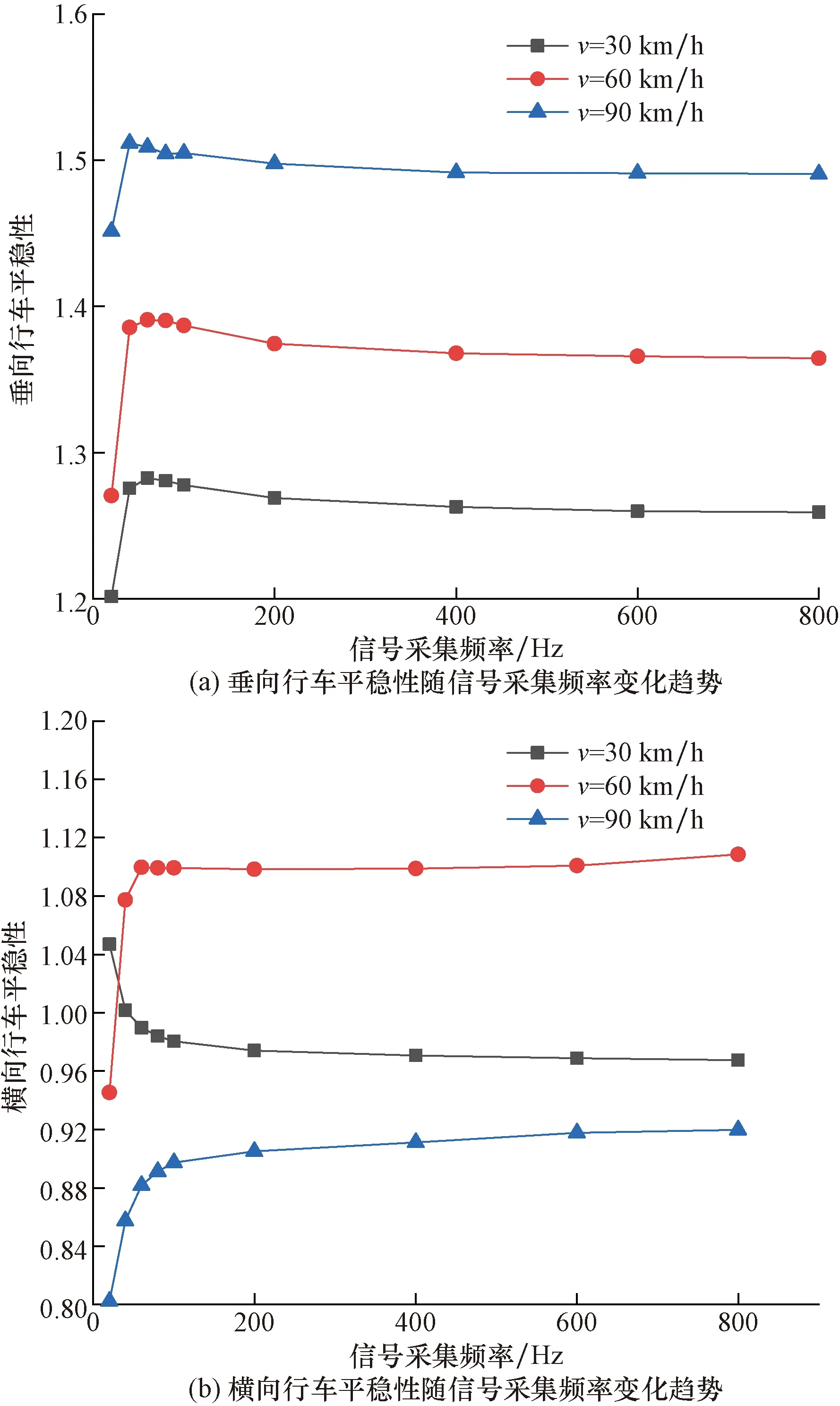
圖6 不同車速下車輛行車平穩性隨信號采集頻率變化趨勢Fig.6 The ride stability of vehicles at different speeds varies with the signal acquisition frequency

由圖6可以看出,在行車平穩性指標處于穩定階段時,車輛垂向平穩性指標隨著車速增加而增大,橫向平穩性指標隨著車速從30 km/h提升至60 km/h時略微上升,而后車速提高到90 km/h時橫向平穩性指標有所下降;在行車平穩性趨于穩定的200～800 Hz采集頻率區段,車速在30～60 km/h時,垂向與豎向行車平穩性指標最大差值分別為0.23和0.19,因此,車速對垂向行車平穩性的影響大于對橫向平穩性的影響。車速對車輛行車平穩性影響規律與文獻[9]中計算值得出規律基本一致,這也間接證明了本文分析方法及數值模型的正確性。

對比各工況下車輛行車平穩性隨信號采集頻率變化趨勢可知,對于車輛垂向行車平穩性指標,當信號采集頻率從20 Hz升高到40 Hz時,幅值精度大幅提高,信號采集頻率于40 Hz增大至200 Hz時,信號混疊逐漸減少使得垂向行車平穩性指標減小,信號采集頻率達到200 Hz之后,垂向行車平穩性指標趨于穩定;對于車輛橫向行車平穩性指標,在信號采集頻率從20 Hz升高到200 Hz過程中,車速為60 km/h和90 km/h的幅值精度不斷提高,車速為30 km/h時,出現信號混疊,隨著采樣頻率的增大,混疊程度逐漸減小,同樣,信號采集頻率達到200 Hz以上后,橫向行車平穩性指標趨于穩定。

2.2 信號采集頻率對軌道梁響應的影響

軌道梁振動信號采集點位于跨中底部,加速度傳感器信號采集頻率范圍為200～3 000 Hz,在自車輛開始上橋到車輛完全出橋這一時間段內進行振動加速度信號采集,得到的軌道梁跨中振動時程曲線,圖7即車速60 km/h時,信號采集頻率為200 Hz和2 000 Hz下的軌道梁振動加速度時程曲線對比圖。觀察對比圖可知,信號采集頻率提高為2 000 Hz時,更多高頻信號被采集到,有效減少了實際的高頻信號被低頻采樣而混疊輸出為低頻信號。

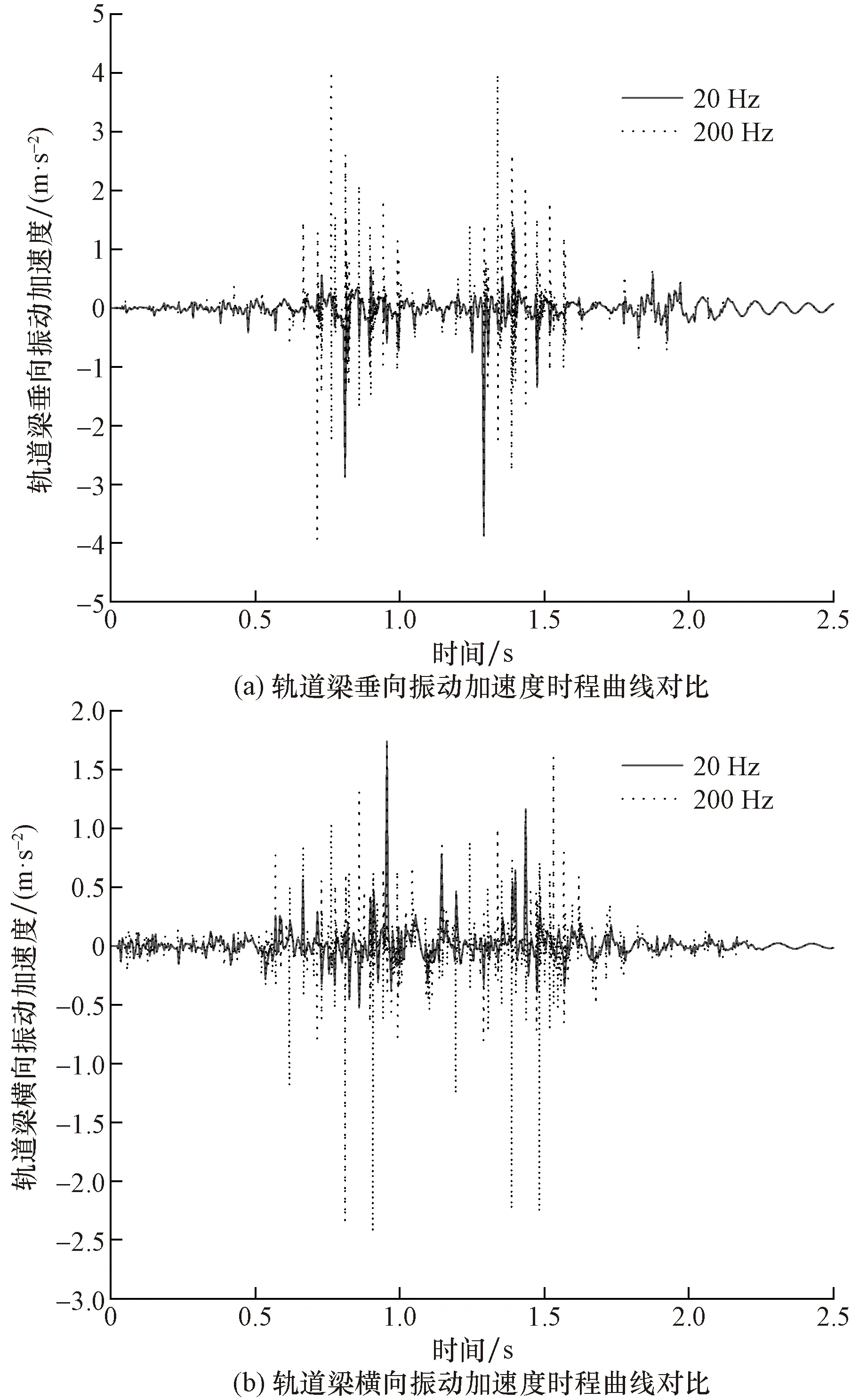
圖7 200 Hz和2 000 Hz采樣頻率下的軌道梁振動加速度時程曲線對比Fig.7 Comparison of vibration acceleration time history curve of track beam at 200 Hz and 2 000 Hz sampling frequency

將信號采集得到的軌道梁振動加速度時程曲線通過40 Hz低通濾波處理得到如圖8所示的不同車速下軌道梁振動加速度隨信號采集頻率變化的趨勢。

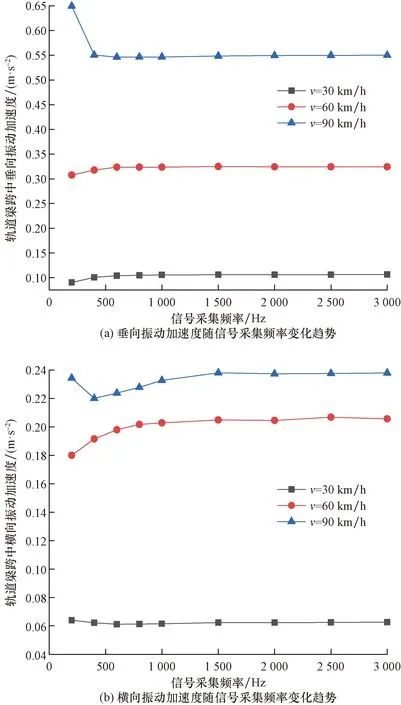
圖8 不同車速下軌道梁振動加速度隨信號采集頻率變化趨勢Fig.8 The dynamic acceleration of rail beam varies with signal acquisition frequency at different speed

對比各工況下軌道梁振動加速度隨信號采集頻率變化趨勢可知,對于軌道梁垂向振動加速度,當信號采集頻率從200 Hz升高到600 Hz時,信號混疊得到有效控制,幅值精度大幅提升,當信號采集頻率達到600 Hz以上后,軌道梁垂向振動加速度趨于穩定;對于軌道梁橫向振動加速度,當信號采集頻率從200 Hz升高到1 500 Hz時,信號混疊程度減弱,滿足幅值精度要求,當信號采集頻率達到1 500 Hz以上后,軌道梁橫向振動加速度趨于穩定。車速為30 km/h時,軌道梁振動響應較弱,隨著信號采集頻率的增大,軌道梁振動加速度變化較小。

3 結論

采用有限元分析軟件,建立跨座式單軌車軌耦合模型,探究不同車速工況下,減少信號混疊、滿足幅值精度要求的跨座式單軌車輛與軌道梁振動信號采集頻率范圍,得出如下結論。

(1)跨座式單軌車軌耦合系統振動信號采集頻率偏低時,會導致車輛與軌道梁振動響應結果嚴重失真;信號采集頻率過高時,對信號幅值精度提升效果并不明顯,還會增大計算時長,占用計算資源。

(2)單軌車輛振動加速度信號采集頻率應不低于200 Hz;行車平穩性結果趨于穩定時的信號采集頻率范圍不受車速的影響。

(3)軌道梁垂向振動加速度信號采集頻率應不低于600 Hz,橫向振動加速度信號采集頻率應不低于1 500 Hz;車速低于30 km/h時,振動信號采集頻率對軌道梁振動加速度準確性影響較小,但隨著車速的升高,信號采集頻率對軌道梁振動加速度結果的影響增大。