基于深度殘差網絡的(n,1,m)卷積碼盲識別

劉 杰,朱宇軒,馬 鈺

(1.軍事科學院系統工程研究院,北京 100191;2.電磁空間認知與智能控制技術重點實驗室,北京 100191)

0 引言

現代數字通信系統中,為保證信息穩定可靠傳輸,往往在調制前對信息序列采用糾錯編碼技術,以實現接收端數據的檢錯糾錯。無論是民用領域的認知無線電系統,還是軍事領域的非合作信息截獲技術,糾錯編碼盲識別技術正日益發揮著重要作用[1-5]。

(n,1,m)卷積碼作為最早被發明的糾錯編碼技術之一,因編譯碼技術成熟、糾錯能力較強,目前已被廣泛應用于電話、衛星和無線信道的數據傳輸中。針對(n,1,m)卷積碼的盲識別問題,目前公開發表文獻中所提方法主要存在兩方面的不足:一是對誤碼的容錯性較差,比如文獻[6]中基于關鍵模方程得到的Gr?bner基約化算法,文獻[7]中基于多項式輾轉相除得到的歐幾里得算法,文獻[8-14]中根據接收序列矩陣化簡后秩虧和列向量分布得到的矩陣分析法等。在實際環境,特別是非合作條件下,受噪聲、干擾和信號預處理誤差的影響,解調、解交織以后得到的二元編碼序列中往往存在很多誤碼,從而約束了上述方法的實用性。二是在假定預知很多先驗信息的條件下,才能完成部分參數的識別。比如Gr?bner基約化算法、歐幾里得算法和文獻[15-17]提出的沃爾什-哈達瑪變換(Walsh-Hadamard Transform,WHT)算法均在碼長、編碼約束長度、碼字起點已知的情況下完成對生成多項式的識別。因此,目前僅有矩陣分析法能較完整的完成(n,1,m)卷積碼識別,其他方法或結合矩陣分析法進行預處理,從而限制了整體識別準確性,或從不同起點和長度順序截取編碼序列,經多次迭代完成碼長等參數的驗證,整個過程比較繁瑣。

由以上分析不難發現,(n,1,m)卷積碼識別的關鍵在于碼長n、碼字起點和存儲級數m的識別。針對傳統方法存在的不足,本文提出了一種基于殘差網絡(Residual Network,ResNet)的(n,1,m)卷積碼盲識別新方法。首先利用常用的(n,1,m)卷積碼在不同誤碼率下生成編碼數據,然后直接按制定長度隨機劃分,輸入ResNet完成監督學習。實驗結果驗證了所提方法的有效性,無需其他先驗信息,即可完成碼長、編碼約束長度和碼字起點的識別,且容錯性能明顯優于傳統方法。

1 問題描述

對于(n,1,m)卷積碼,參數n、m分別表示碼長和存儲級數[18-19]。令s(x)表示卷積碼信息序列,C(x)表示編碼序列,G(x)表示生成多項式矩陣,則編碼方程在環F2(x)上可表示為:

C(x)=s(x)·G(x),

(1)

式中:

(2)

(3)

且

(4)

gi(x)=gi,0+gi,1·x+…+gi,m·xm,i=0,1,…,n-1,

(5)

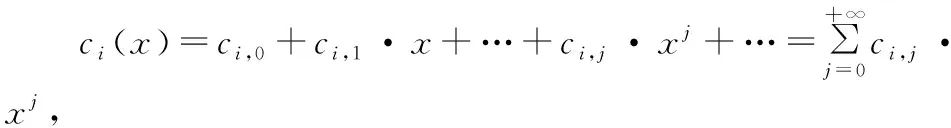
(6)

設傳輸時對應誤碼多項式矩陣為:

(7)

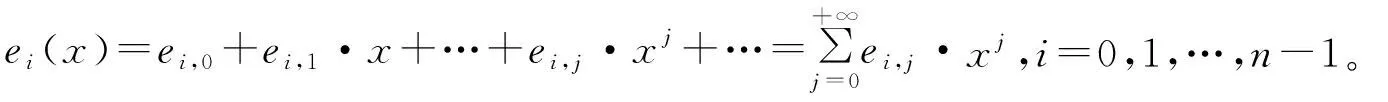
i=0,1,…,n-1。

(8)

為便于分析,將上式轉化為二元比特流形式,則:

V=(vk-1,l,vk-1,l+1,…,vk-1,n-1,vk,0,vk,1,vk,2,…,
vk,n-1,vk+1,0,vk+1,1,…,vk+M,p,vk+M,p+1)。

(9)

可以看出,去除編碼序列V首尾兩組不完整的碼字,中間共有M組完整的碼字。卷積碼盲識別是在僅知道序列V的前提下,通過合適的方法恢復出碼長n、碼字起點vk,0和存儲級數m等參數,進而計算得到生成多項式。

2 基于ResNet的(n,1,m)卷積碼識別

2.1 模型結構設計

深度神經網絡[20]屬于機器學習算法的一個重要分支,目前已被廣泛應用于計算機視覺、自然語言處理等領域。本文考慮到卷積編碼的數據特征,采用卷積神經網絡中的ResNet模型進行訓練,其基本組成結構如圖1所示,共兩種形式,圖中3×3表示卷積核大小,64表示輸出通道的維數。與普通卷積神經網絡相比,ResNet模型將輸入直接傳到網絡輸出,使得學習目標變成了期望輸出與輸入的差值,進而避免了深層次卷積神經網絡模型中的模型性能退化的問題,得到了更好的性能。

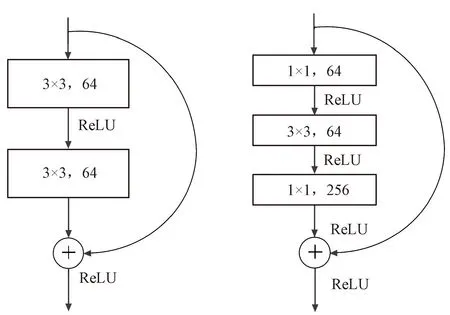
圖1 ResNet典型殘差單元結構示意圖Fig.1 Architecture of ResNet model

常用的ResNet結構網絡深度分別為18、34、50、101和152,主要針對多維數據,而信道編碼的數據是二元序列,為一維數據。因此,本文結合問題的難度,選擇基于Pytorch 中的ResNet-18、ResNet-50網絡結構進行調整,構造適用于信道編碼的ResNet網絡模型,其中,基于ResNet-50模型用于對編碼結構的識別,ResNet-18用于對碼序列起點的識別。將原網絡中,卷積核“1×1”“3×3”“7×7”變成“1×1”“1×5”“1×7”,卷積方式由二維卷積變為一維卷積,得到網絡結構示意圖如圖2所示。

(a) 編碼結構識別網絡模型

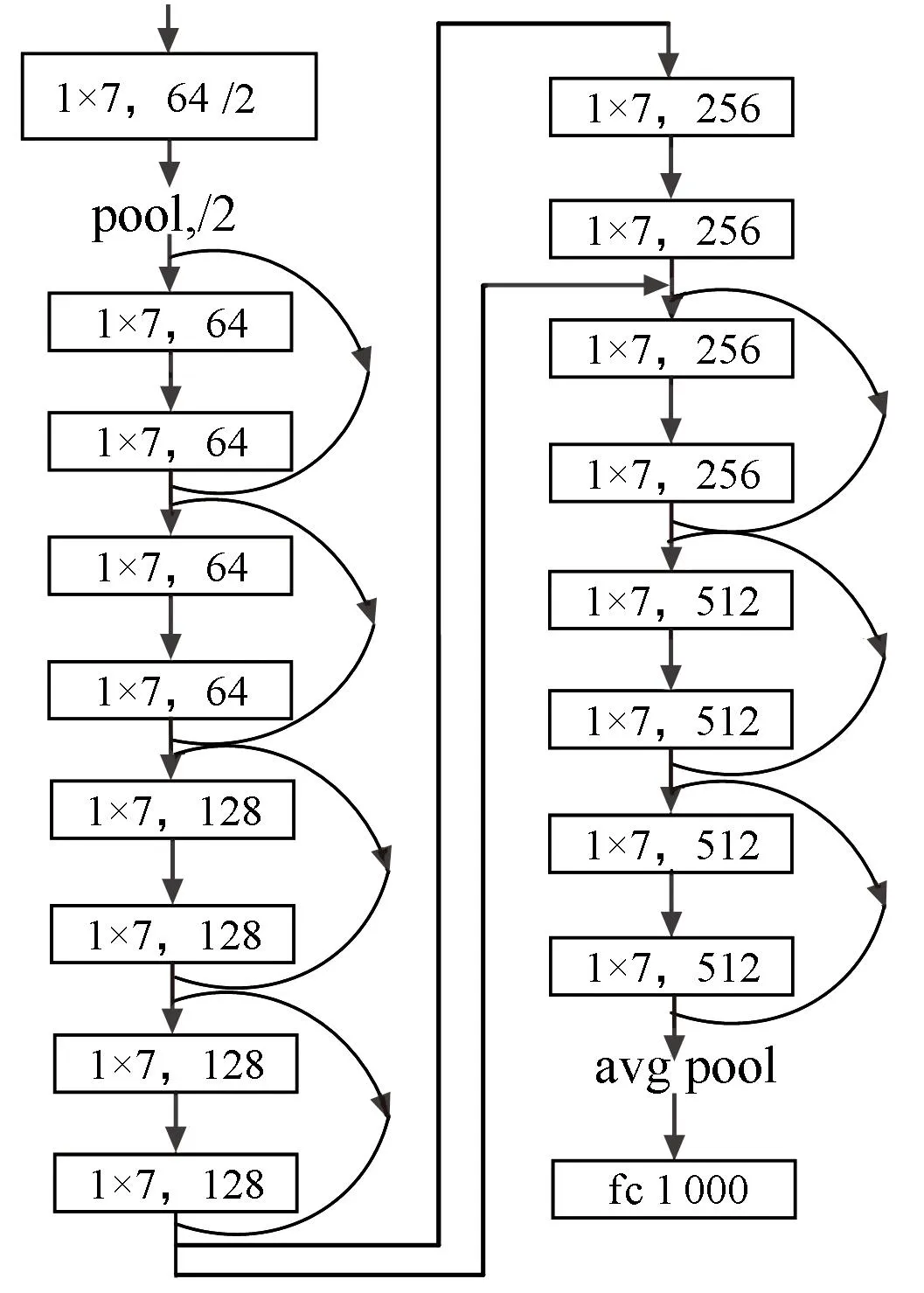
(b) 碼序列起點識別網絡模型圖2 本文調整后的ResNet模型Fig.2 Adjusted ResNet model

2.2 網絡數據樣本生成

本文采用監督學習算法,基于常用的(n,1,m)卷積碼在不同信噪比下構造數據樣本,并對網絡進行訓練,實際識別時將待識別數據序列輸入網絡即可得到識別結果。根據文獻[15],本文選取碼長分別為2、3、4,編碼存儲級數為1～7的共21種常用碼,用來構造數據。由前文分析可知,經解調等預處理后,最終影響識別效果的是誤比特率和碼字起點,因此可以利用計算機仿真軟件非常方便地構造數據集。對于每一組碼長n和存儲級數m下,選取誤比特率為0(即無誤碼)、0.01～0.09共10種情況,比特序列起點離碼字起點為0～n-1共n種情況,分別在每種組合下構造30 000個200 bit長度的數據,其中錯誤比特根據編碼序列長度和誤比特率隨機加入。同時,考慮卷積編碼序列中前后比特的相關性,為了保證每個數據之間彼此獨立,并不從一條編碼數據中順次截取數據。而是每次隨機生成長度為1 000 bit的數據序列,然后按誤比特率隨機加入誤比特,最后根據設置的數據起點從中截取長度為200 bit的數據。

2.3 模型訓練與識別步驟

訓練編碼結構識別模型時,將所有數據送入網絡進行訓練,總樣本數為1.89×107;訓練編碼序列起點識別模型時,分別選取對應碼長、編碼存儲級數下n種樣本序列起點、10種誤比特率下n×10×30 000個樣本進行訓練,共需訓練21個識別模型。兩種網絡訓練均按4∶1的比例隨機劃分數據,得到訓練集和驗證集。

根據以上分析,總結基于ResNet的(n,1,m)卷積碼識別步驟如下:

① 針對表中所示的21種(n,1,m)卷積碼,按1～21 依次進行編號,對于每種編號下卷積碼,利用Matlab軟件按照2.2節所示生成訓練樣本;

② 將所有樣本混合均勻后按4∶1的比例隨機劃分數據,得到編碼結構識別訓練集和驗證集;分別選取對應碼長、編碼存儲級數下n種樣本序列起點、10種誤比特率下n×10×30 000個樣本,得到21個子樣本集,各自混合均勻后按4∶1的比例隨機劃分數據,得到編碼序列起點識別訓練集和驗證集;

③ 基于Pytorch框架分別構建圖2所示的編碼結構識別網絡模型和編碼序列起點識別網絡模型,將訓練集樣本輸入各自網絡進行訓練,并根據驗證集情況不斷調整網絡參數,直到在驗證集上結果最優;

④ 對于待識別的卷積碼序列,按長度200 bit劃分得到多個數據樣本,輸入到編碼結構識別網絡模型,根據統計結果確認待識別的編碼結構,然后將編碼序列從起點開始,每次間隔碼長n劃分序列得到多個數據樣本,輸入所對應編碼結構的編碼序列起點識別模型,根據統計結果確認待識別的編碼起點,識別完成。

3 仿真驗證與分析

仿真軟件基于Windows 10 64位系統,數據產生基于Matlab R2020a 64位,程序設計基于Pycharm 2021.01社區版,Pytorch框架版本為1.5.1,cuDNN版本為7.6.1。硬件配置為:Intel(R) Core(TM) i9-10900X CPU @3.7 GHz,128 GB RAM,Nvidia GeForce RTX 2080Ti。

3.1 方法有效性驗證

按2.2節生成訓練集和驗證集,輸入網絡進行訓練,迭代30次后統計測試集上每種編碼類型的識別成功率,得到的混淆矩陣如圖3所示。

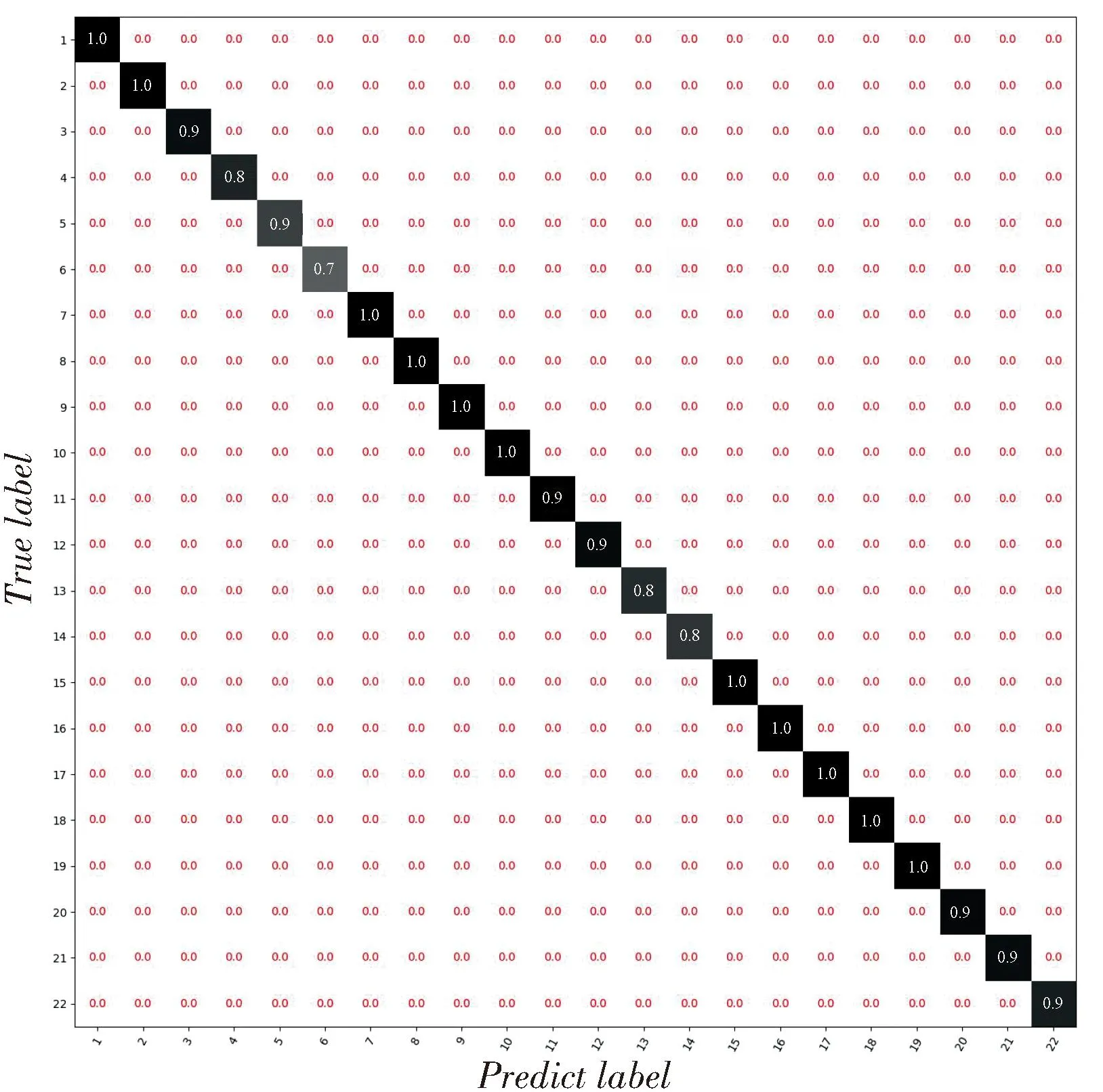
圖3 21種編碼樣式綜合識別準確率Fig.3 Comprehensive recognition accuracy of 21 convolutional coding structure

圖中,縱軸代表樣本的實際標簽,橫軸代表網絡預測的標簽,二者對應的紅色數值表示實際標簽對應樣本被識別為預測標簽對應編碼樣式的概率,即矩陣對角線處的數值表示21種編碼樣式在不同誤比特率下的綜合識別準確率。可以看出,對于21種編碼樣式,在誤比特率為0.01～0.09時,綜合識別準確率至少大于77.3%。進一步地,按2.2節相同的方法生成數據序列,從中隨機截取長度為200 bit的數據,每種情況下生成3 000個樣本。列出所有編碼樣式隨誤比特率的識別準確率變化曲線,結果如圖4所示。可以看出,在誤比特率小于0.03時,對所有編碼樣式的識別準確率均達到90%以上,甚至部分編碼樣式在誤比特率為0.09時識別準確率達到了97%。這證實了本文所提方法的有效性。

(a) 1/2碼率卷積碼識別結果

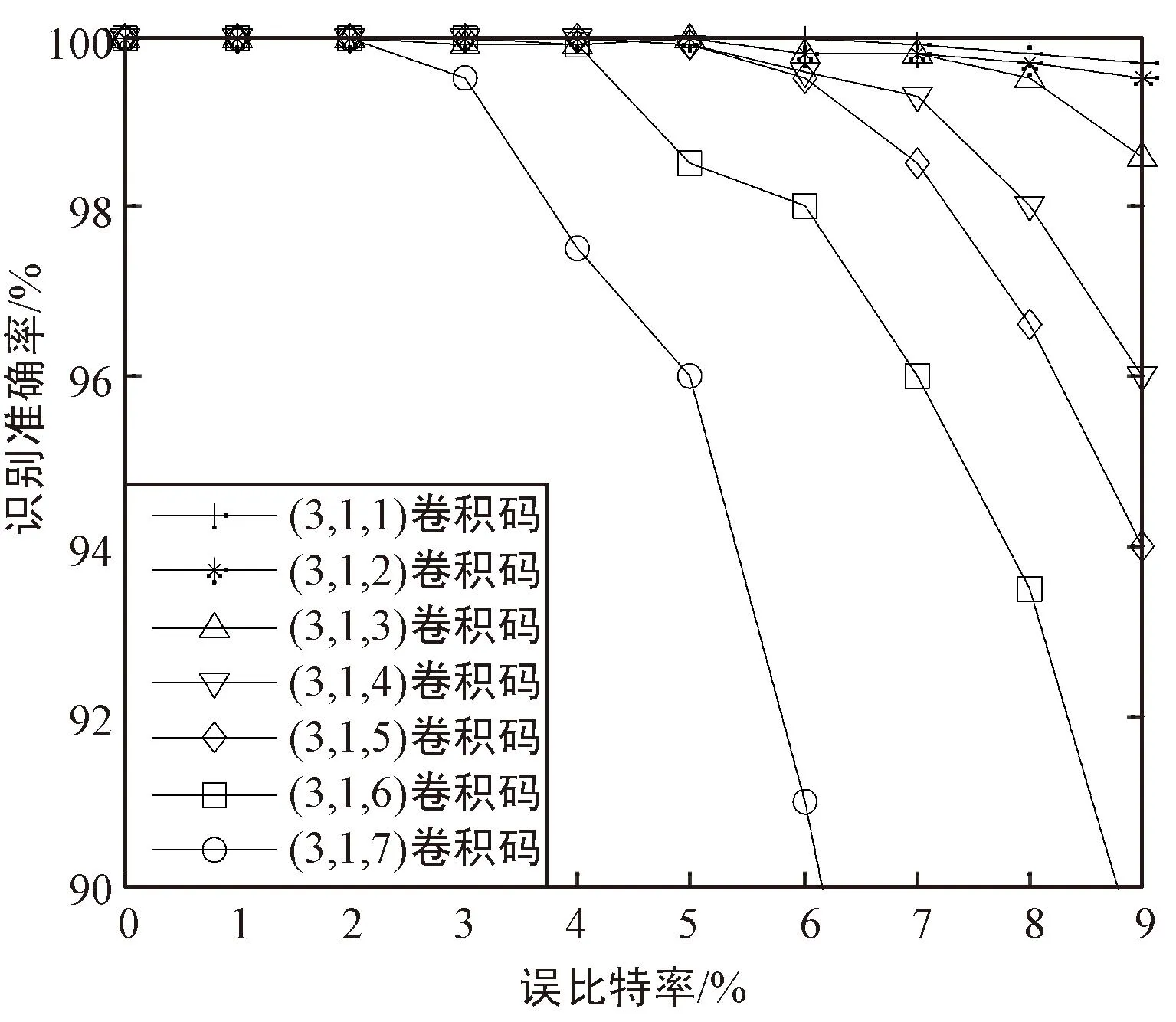
(b) 1/3碼率卷積碼識別結果

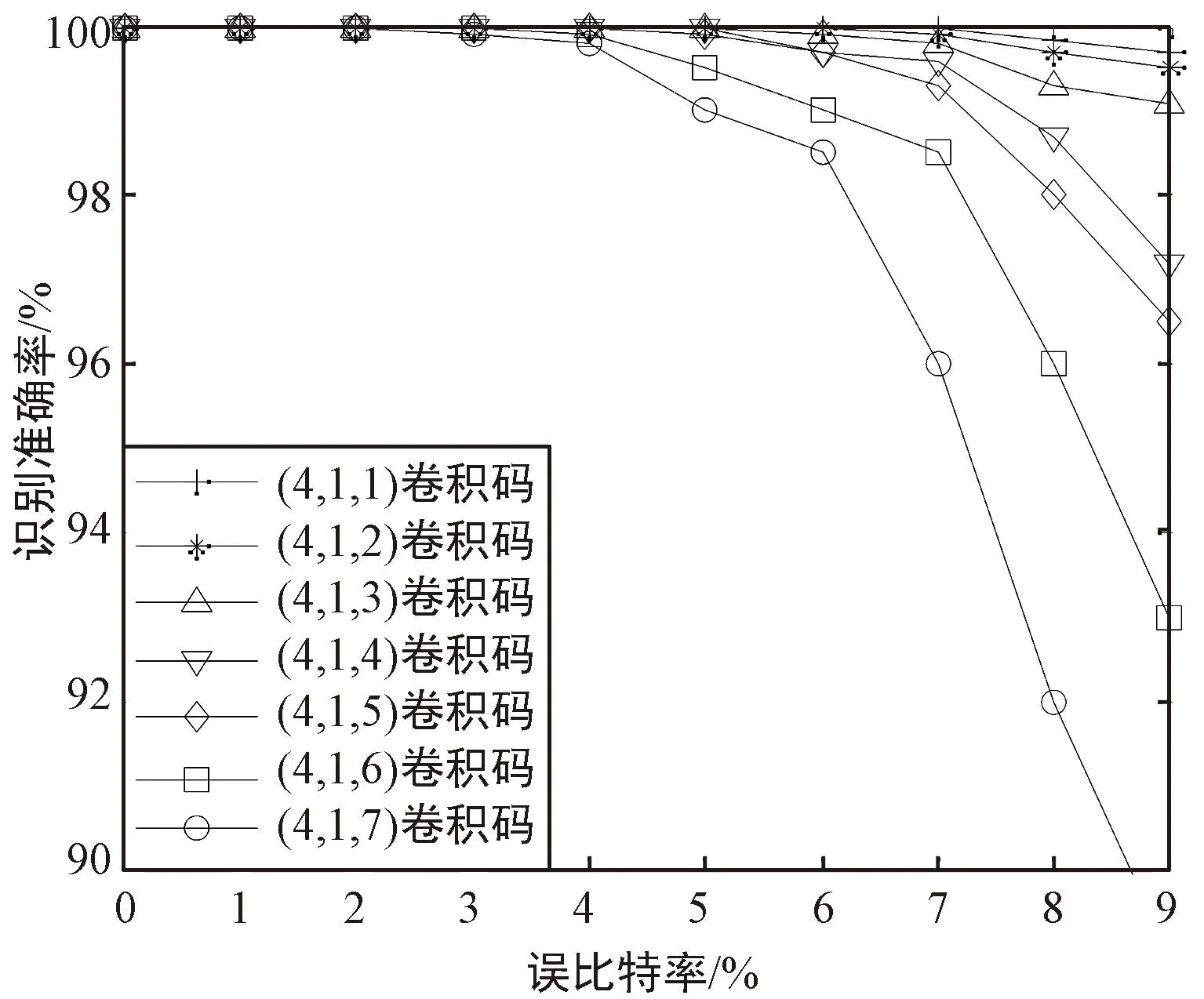
(c) 1/4碼率卷積碼識別結果圖4 不同誤比特率下卷積碼識別準確率Fig.4 Recognition accuracy of convolutional codes under different bit error rates

對于編碼序列起點識別,以(2,1,5)、(3,1,5)、(4,1,5)卷積碼為例,在訓練集上完成網絡訓練后,在驗證集上的統計每種編碼起點的識別成功率,得到的混淆矩陣如圖5所示。

(a) (2,1,5)卷積碼識別結果

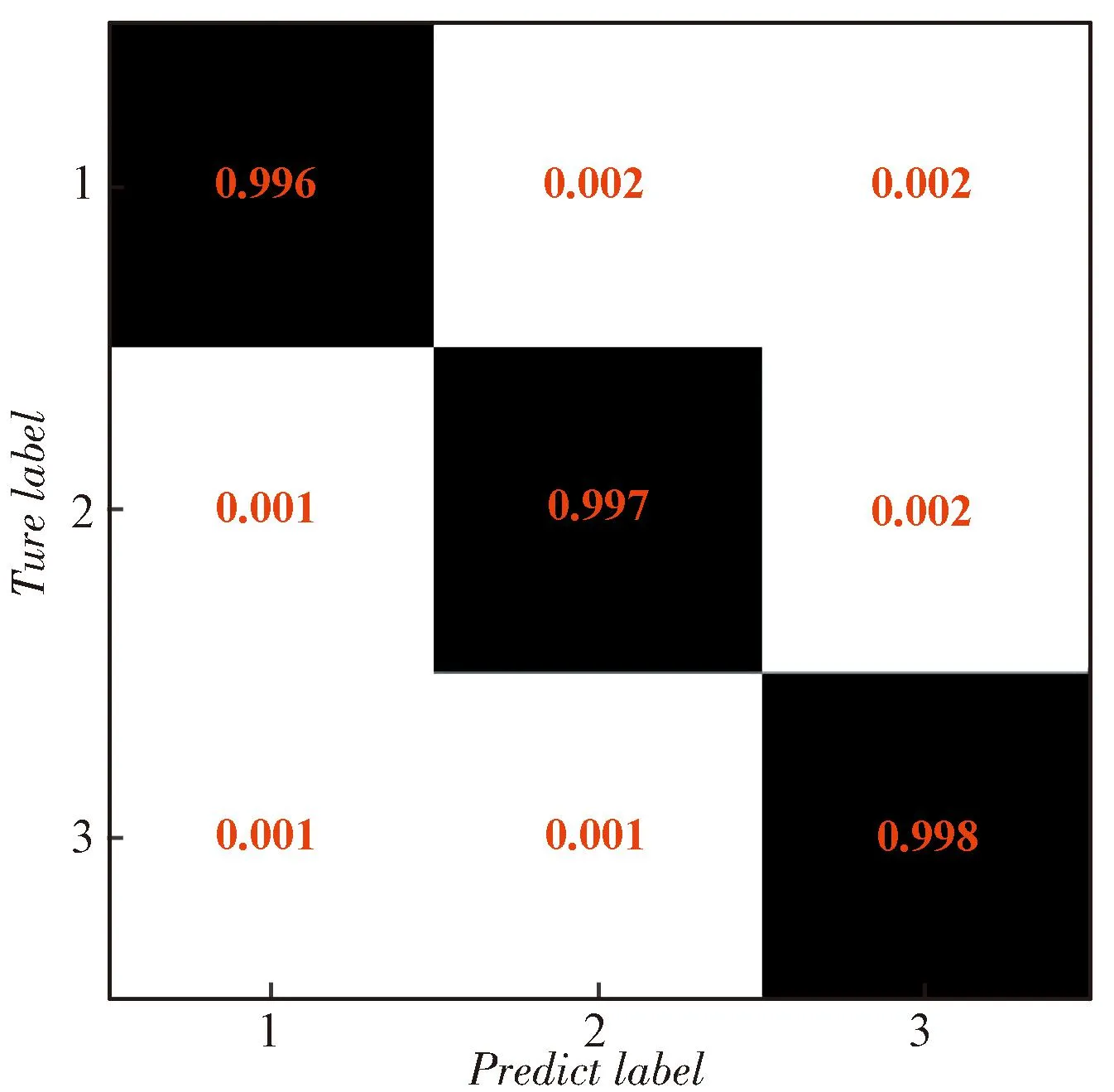
(b) (3,1,5)碼率卷積碼識別結果

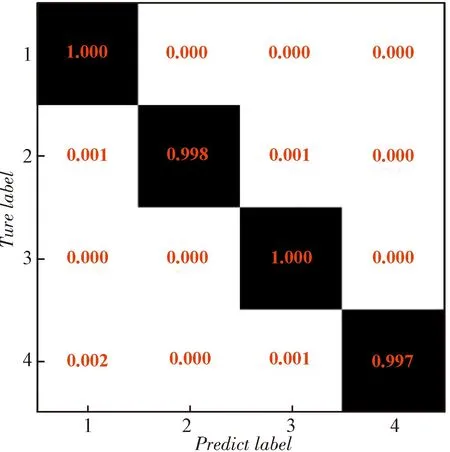
(c) (4,1,5)碼率卷積碼識別結果圖5 編碼起點識別結果Fig.5 Recognition result of coding starting point

可以看出,在不同情況下,每種起點情況的識別準確率都在96%以上。證實了本文所提方法的有效性。

3.2 與傳統方法的對比

對卷積碼識別,目前常用的方法主要是基于矩陣分析的方法和基于檢驗關系遍歷驗證的方法。下面主要從誤比特率的適應性、計算復雜度、對數據長度的需求,以及碼序列起點、碼長和編碼記憶長度對識別的影響等幾方面進行對比,說明本文方法的優勢之處。

3.2.1 識別性能對比

首先將本文方法對誤比特率的適應性與文獻[9]中基于矩陣分析的方法、文獻[16]中基于最大似然檢測的方法進行識別性能對比。選取(3,1,5)卷積碼進行研究,由于不同方法所需的數據量并不相同,為了對比的客觀性,此處主要考慮各種方法的最佳識別性能(即各種方法均滿足識別所需的條件),得到結果如圖6所示。

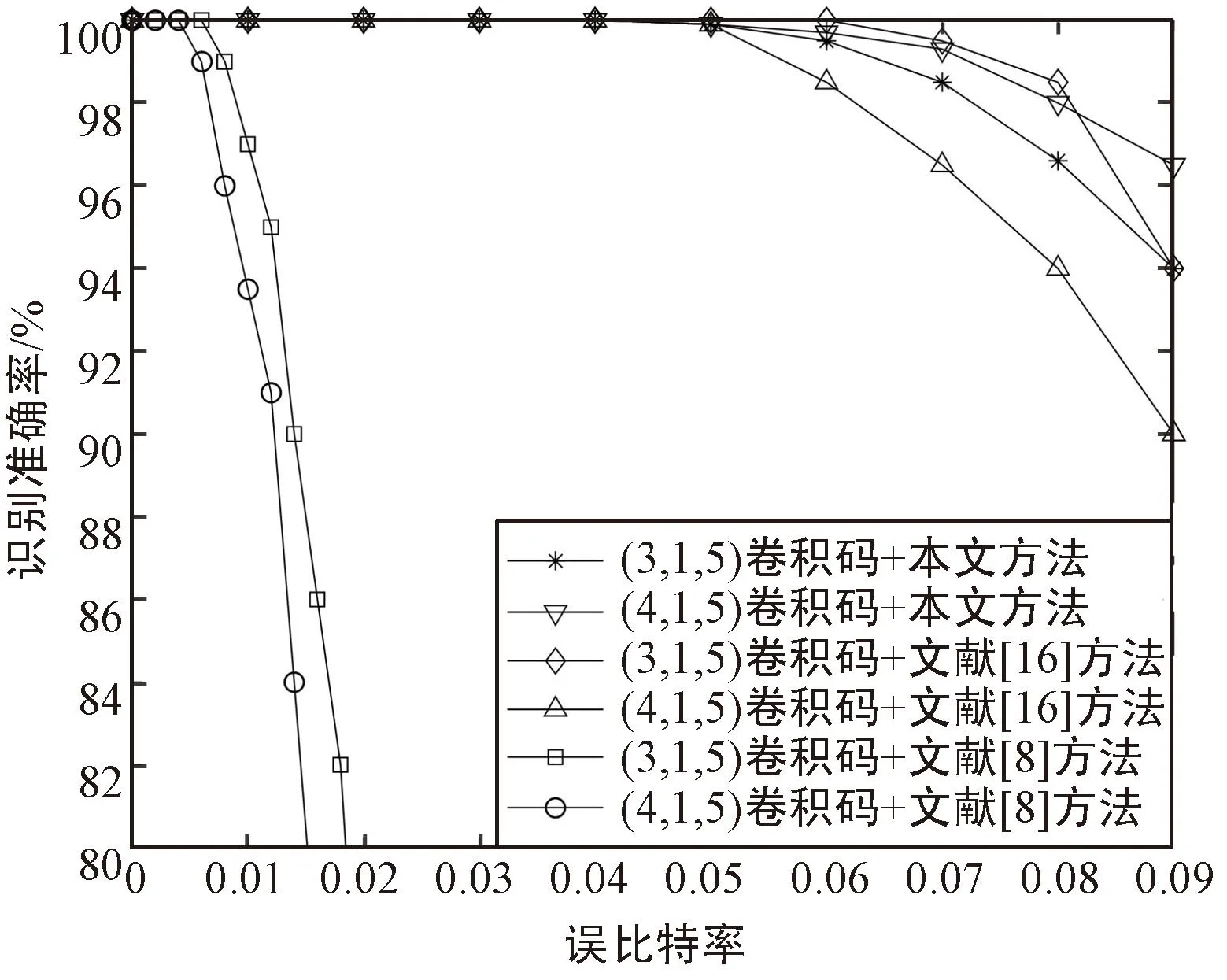
圖6 不同方法識別性能對比Fig.6 Comparison of recognition performance between different methods

可以看出:

① 在理想情況下,本文的識別準確率與文獻[16]中方法基本相當,明顯優于文獻[9]中方法,能在誤碼率為0.09時達到90%以上的識別概率;

② 兩種對比方法在碼長增大時識別模型更容易受到誤比特的影響,導致識別率下降,本文方法在碼長增大時識別率反而上升,可能是因為碼長較大時編碼數據包含的特征更明顯,從而使網絡更容易被訓練。

同時,還應考慮到不同方法在識別時需要的編碼參數先驗知識并不相同。本文方法和文獻[9]中方法不受先驗知識的影響,直接將接收序列輸入識別模型即可識別出對應的碼長、編碼記憶長度、生成多項式等參數,而文獻[16]中方法需要預知碼長、校驗多項式階數以及編碼起點等知識,否則無法建立有效的方程進行識別。在實際應用場景下先驗知識往往很難獲取,因此文獻[16]中方法的運用限制更大。

3.2.2 計算復雜度對比

對于本文方法,計算量主要在于網絡的訓練過程,但由于網絡模型可以提前訓練,而實際識別時往往需要近實時處理,因此,與文獻[9,16]中的方法進行計算量對比時,主要對比識別時的計算量,對于本文方法即測試過程的計算量。

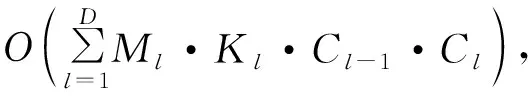
Ml=(Ml-1-Kl+2Pl)/Sl+1。

(10)

根據圖4可知,網絡包含卷積層數為49,卷積核長度取值為1或5,P取值為1或3,S取值為1或2,根據以上參數可以計算識別所需的計算復雜度。文獻[9]中方法計算復雜度為Ο(25·L3/14),其中L取值為49;文獻[16]中方法計算復雜度為Ο(N·n·(K+1)·2n(K+1)),其中n為碼長,N為建立的方程組系數矩陣的行數,K為校驗多項式的最高階數。計算文中21種卷積碼的計算復雜度如圖7所示。

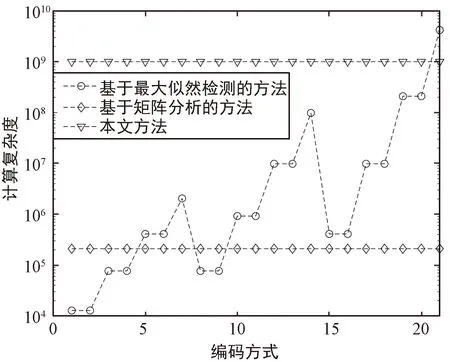
圖7 不同方法計算復雜度對比Fig.7 Comparison of calculation complexity between different methods

可以看出,本文方法的計算復雜度保持恒定,在編碼參數較小時大于兩種傳統方法,但隨著編碼參數的增大,基于最大似然檢測的方法計算復雜度逐漸超過本文方法。

3.2.3 對數據長度的需求

本文識別方法網絡訓練的數據可以用通過計算機仿真生成,識別時所需的數據量與網絡訓練時選擇的樣本長度相同,恒定為200,而文獻[9,16]中的方法往往與編碼參數有關。文獻[9]建立分析矩陣的列數要大于編碼約束長度n·(m+1),在本文選擇的21種編碼方式下,取列數為30,行數為35,每行的起點間隔取12,則建立分析矩陣的過程所需數據量至少為438。文獻[16]方法與誤比特率、方程解的重量(即解向量中1的個數)有關,誤比特率越高、方程解的重量越大,所需數據量越多。本文取校驗多項式階數為K=「(m+1)/2?,方程解的重量為ω=「n(「(m+1)/2?+1)/2?,誤比特率取0.09,則所需數據量為:

(11)

計算21種編碼方式所需的數據長度,結果如圖8所示。可以看出,本文識別方法所需數據長度小于兩種對比方法,特別是文獻[16]中的方法,在碼長、編碼記憶長度較大情況下差距能達到數百倍。

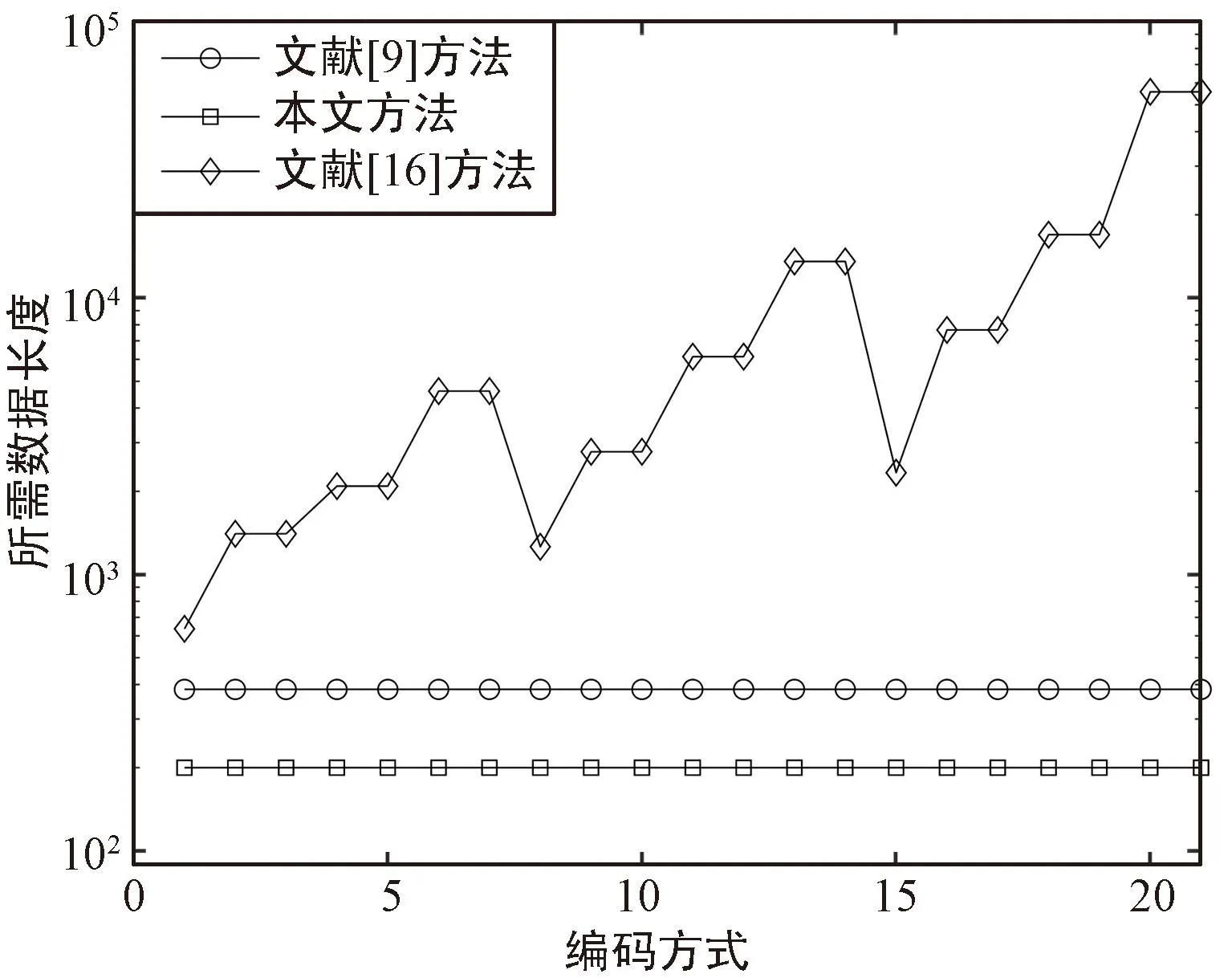
圖8 不同方法識別對數據長度的需求對比Fig.8 Comparison of sequence length needed for recognition between different methods

4 結束語

本文提出了一種基于ResNet的(n,1,m)卷積碼盲識別新方法,將圖像識別領域常用的神經網絡模型經改造應用于信道編碼識別領域,由網絡提取不同編碼參數下的差異特征,改變了傳統人工提取特征進行卷積碼參數識別的思路,可有效提升高誤比特率下的識別準確率,且識別所需數據量有效降低,更適用于非合作條件下的信道編碼盲識別。

下一步將重點關注刪余卷積碼、線性分組碼、Turbo碼等編碼類型和參數的識別,將基于深度學習的識別模型擴展至其他編碼類型,進一步提升實際工程應用價值。