多級壓裂套管偏心條件下微環隙發展規律研究

丁建新 席 巖 姚 宇 王海濤 溫 欣 李 輝

(1.昆侖數智科技有限責任公司 2.北京工業大學)

0 引 言

井筒密封完整性是保障油氣井安全和延長油氣井生命周期的重要保障[1-3]。水力壓裂作為增產的主要措施，施工過程中井筒內壓頻繁升高、降低，容易導致套管-水泥環-地層界面出現微環隙，進而誘發井筒密封完整性失效(環空帶壓)[4-5]。針對此，部分學者和工程技術人員開展了一系列的研究：劉仍光等[6]利用全尺寸水泥環密封性試驗裝置，研究了套管居中時內壓循環加卸壓條件下水泥環應力應變狀態，指出套管-水泥環界面處易出現變形不協調，進而導致微環隙產生；劉洋等[7-8]對川中多口高壓氣井環空帶壓進行了分析，建立了套管居中條件下交變載荷作用下水泥環彈塑性變形模型，指出微環隙的產生是導致環空帶壓的主要原因；趙效峰等[9]針對油氣井生產過程中固井界面微環隙的產生和發展開展了仿真試驗，結果表明相同膠結質量下固井一界面比二界面更容易產生微環隙；XI Y.等[10]基于套管居中的實際條件，開展了室內全尺寸水泥環試驗和數值模擬研究，指出套管-水泥環界面在套管內壓循環加卸載過程中出現了微環隙，分析了循環加卸載次數對于微環隙產生和發展的影響規律。前人在開展循環加卸載作用下微環隙產生與發展室內試驗和數值模擬過程中，通常假定套管居中、水泥環完整，這與長水平段水平井水平段套管易偏心的實際并不相符，且斯倫貝謝公司在北海等多個地區工程實踐結果表明，套管偏心會對水泥環密封完整性帶來顯著影響，加劇井筒密封完整性失效的風險[11]。黃熠等[12]通過開展室內研究也指出，套管偏心容易導致微環隙的出現，進而劣化水泥環的密封完整性。以上研究均未對套管偏心條件下、循環加卸載過程中水泥環微環隙產生的機理和發展規律進行分析，未對比和量化套管居中和偏心條件下水泥環微環隙發展規律的差異性，亟待開展進一步的研究。

針對此，筆者綜合考慮水力壓裂套管內壓循環加卸載和套管偏心的實際，建立了基于Mohr-Coulomb 準則和損傷理論的套管偏心條件下微環隙產生和發展數值模型，量化了套管居中和偏心條件下微環隙寬度的差異性，研究了多級壓裂過程中不同偏心距、偏心角對于微環隙產和發展的影響規律。研究結果可為井筒密封完整性的控制提供理論支撐和工程參考。

1 工程背景

頁巖儲藏開發過程中往往采用水平井和多級水力壓裂的方法，其中為進一步提升產能使得水平段往往較長(1 500～2 500 m)，容易導致固井過程中套管自重較大產生下沉，進而導致套管偏心、水泥漿凝固后形成的水泥環不規則[13-15]。此外，多級水力壓裂使得施工過程中套管內壓頻繁升高、降低，容易導致套管-水泥環界面出現微環隙，進而導致井筒密封完整性失效。前人在研究過程中，通常以套管居中為前提開展相應的分析，與工程實際不相符，且目前工程實踐和室內試驗表明，套管偏心會加速水泥環微環隙的發展，進而加劇井筒密封完整性失效的風險[11]。

頁巖氣井套管偏心狀態如圖1所示。

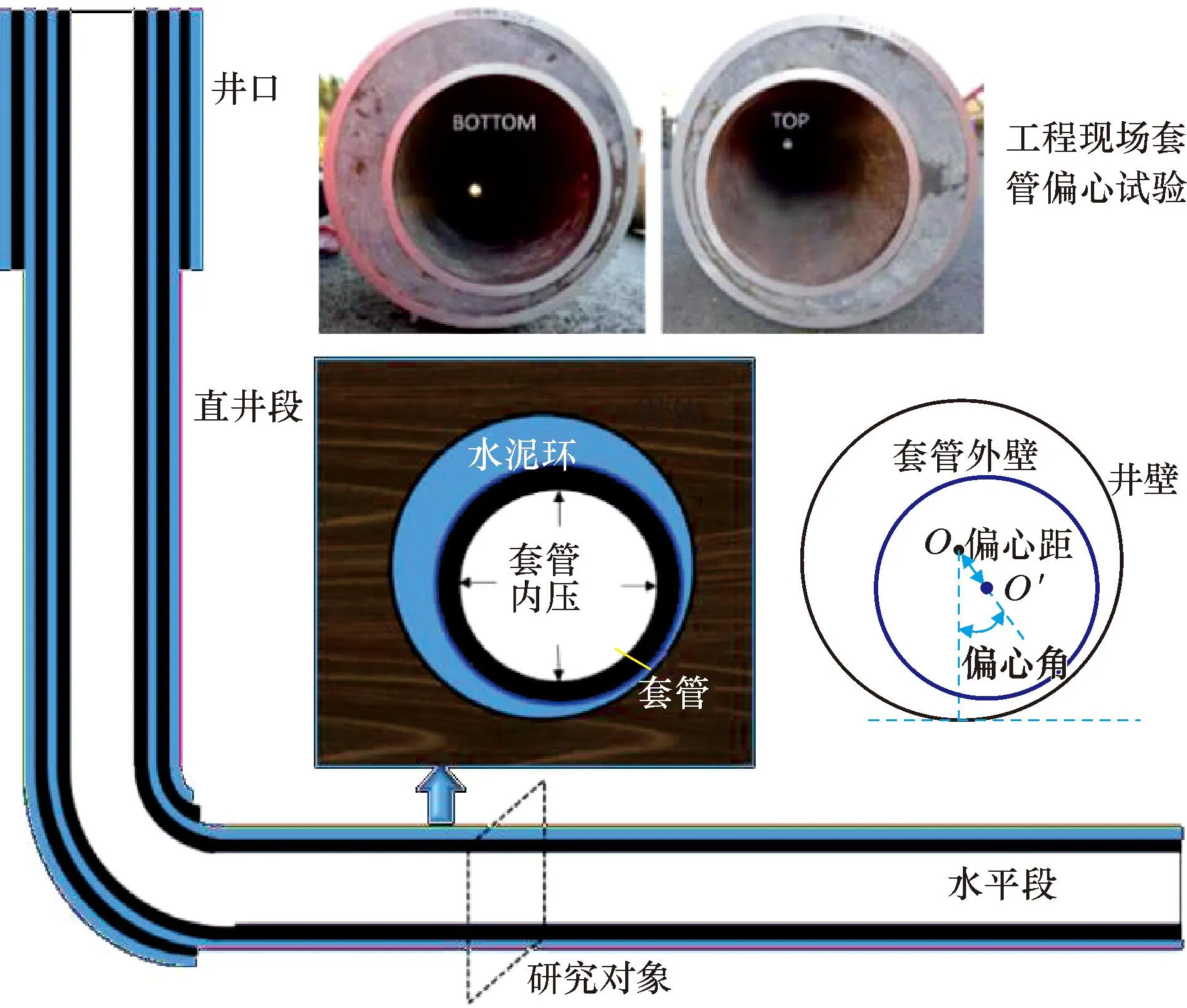
圖1 頁巖氣井套管偏心狀態Fig.1 Eccentric state of casing in shale gas well

頁巖氣井水平段套管偏心狀態下，在三維非均勻地應力的作用下，導致套管-水泥環界面沿圓周受力不均勻，在套管居中條件下就會導致其微環隙發展沿圓周存在差異性，套管偏心時會加劇該差異性。為進一步量化分差異性產生的機制，采用偏心距和偏心角對于套管偏心的狀態進行量化，其中偏心距會影響水泥環的壁厚分布，偏心角則會影響窄環隙處承受載荷的方向，進而對微環隙產生與發展的規律帶來影響。研究過程中，選擇井筒的水平段為研究對象，定義井眼圓心與套管圓心之間的距離為偏心距，定義井眼圓心與套管圓心連線與井眼垂線的夾角為偏心角。

2 數值模型

2.1 數值模型建立

三開井身結構是目前頁巖儲層油氣井廣泛使用的井身結構，儲層段井筒組合體主要包含套管、水泥環和地層，基于此建立相應的數值模型，如圖2所示。模型建立過程中，井眼直徑(215.9 mm)以及套管規格(直徑139.0 mm，壁厚9.17 mm)均與當前工程實井井筒工程實際尺寸一致。地層數值模型的大小為3 m×3 m×3 m，模型邊界為井眼直徑的10倍以上，以避免邊界效應對水泥環應力-應變帶來的畸變影響。與此同，模型建立時考慮套管居中和偏心的條件，同時采用偏心距和偏心角量化套管偏心的程度。

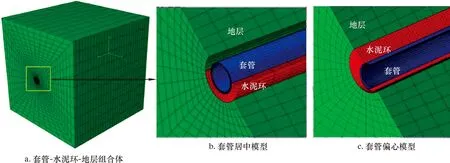
圖2 數值模型及網格劃分Fig.2 Numerical model and grid division

劃分網格過程中，為保障計算結果的精確性和收斂性，采用六面體結構網格對數值模型進行劃分。同時考慮到計算的時效性，對地層采用變密度劃分網格的方法。

2.2 塑性變形破壞準則

多級壓裂過程中，井筒內壓循環加卸載，導致套管-水泥環界面出現塑性變形且不斷累積，進而導致微環隙出現。針對該情況，采用Cohesive黏彈性單元進行模擬。計算過程中，套管內流體的壓力作用在套管內壁上，在徑向上通過傳導作用在水泥環內壁上，在力作用的影響下，水泥環內壁發生變形，且彈性變化階段應變隨著應力的增加逐漸增加；達到彈性階段末端時，材料進入損傷演化階段，對應的應力值或者位移為黏彈性單元損傷起始值。該過程中，套管-水泥環膠結面力學性能不斷退化，塑性變形產生累積，進而導致微環隙出現。

數值模型計算過程中，采用能量損傷演化中的BK準則[16]：

(1)

GS=Gs+Gt

(2)

GT=Gn+Gs+Gt

(3)

(4)

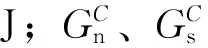
參數設置過程中，參考Wang &Taleghani等[16-17]基于試驗得到的相應結果，如表1所示。

表1 Cohesive單元界面膠結參數Table 1 Cohesive element interface cementation parameters

與此同時，為進一步量化微環隙的寬度，基于所計算出來的塑性變形分析微環隙寬度的發展過程，其中：

εture=ln(1+εnom)

(5)

σture=σnom(1+εnom)

(6)

(7)

式中：εture、εnom分別為真實應變和名義應變，%；σture、σnom分別為真實應力和名義應力，MPa；εture，pl、εture，el、εture，l分別為真是塑性應變、真實彈性應變和真實總應變，%；E為彈性模量，MPa。

2.3 邊界條件與材料參數

模擬過程中，采用瀘州區塊1口實井參數進行計算。該井垂深為3 500 m，壓裂過程中泵壓為77 MPa，壓裂液密度為1.05 g/cm3，排量為12 m3/min。為簡化計算，壓裂級數設置為10級。

邊界條件設置過程中，地層的邊界均設置為零位移、零轉動，以模擬實井地層在井下的穩定條件；采用Predefined Field方式加入三維地層地應力，其中最大水平地應力(σH)、最小水平地應力(σh)和垂向地應力(σv)梯度每100 m分別為3.08、2.43和2.83 MPa，其中σH>σv>σh。在生產套管內壁施加內壓，內壓值計算過程中考慮井口泵壓、水平段特定位置處的靜液柱壓力和摩阻。

在井筒材料參數設置方面，套管、水泥環、地層參數均根據實井數據進行設置。其中：套管彈性模量為206 GPa，泊松比為0.3，屈服強度為758 MPa；水泥環彈性模量為5.5 GPa、泊松比為0.17，內摩擦角和黏聚力分別為30°和8 MPa，模擬開展過程中水泥石遵循Mohr-Coulomb準則；地層彈性模量、泊松比、內摩擦角和黏聚力分別為33 GPa、0.24、50°和10 MPa。

3 結果與討論

3.1 結果驗證與對比分析

3.1.1 累積塑性應變

前人基于套管居中條件，采用室內試驗和數值模擬的方式，開展了循環加卸載條件下微環隙發展室內試驗以及數值模擬分析[3，5-6]。研究結果表明，微環隙主要出現在套管-水泥環界面。圖3為本研究中的計算結果。

由圖3可以看出：循環加卸載前，套管-水泥環-地層界面保持緊密接觸，無微環隙產生；循環加卸載10次后，套管-水泥環界面出現了塑性應變，進而導致微環隙出現，水泥環-地層依然保持緊密接觸。這與前人試驗和計算的結果較為相符，證明了數值模型的正確性。

在此基礎上，進一步考慮存在套管偏心的情況。取偏心距為10 mm、偏心角為0°的條件，對比分析套管內壓循環加卸載條件下套管居中和偏心條件下累積塑性應變規律發展的差異性。當循環加卸載為1次、4次、7次和10次時，累積塑性應變(PEEQ)進行對比分析，結果如圖4所示。基于圖4可以看出：

圖4 套管居中和偏心條件下塑性累積應變圖Fig.4 Plastic cumulative deformation of casing under centering and eccentric conditions

(1)套管居中條件下，考慮到井筒方向沿最大主應力方向，水泥環在最小水平主應力和垂向地應力的共同作用下，塑性變形位置主要集中水泥環內壁的兩側區域，平行于最小水平主應力方向。隨著循環加卸載次數的不斷增加，套管內壁累積塑性應變量不斷增大。

(2)套管偏心條件下，在最小水平和垂向地應力的共同作用下，套管-水泥環的幾何位置的改變，影響了累積塑性應變的分布區域。經過一定加卸載循環次數后，平行于垂向地應力的水泥環內壁位置成為了最大塑性應變的區域。與此同時，隨著循環加卸載次數的不斷增加，水泥環內壁的累積塑性應變不斷增加。

(3)套管偏心顯著增大了水泥環內壁的累積塑性應變。對比第7次、第10次循環加卸載條件下套管內壁累積塑性應變最大值，套管居中條件下累積塑性應變值分別為0.565%和0.594%，套管偏心條件下則分別為0.627%和0.770%，相比套管居中條件下分別增長11.0%和29.6%。由此可以看出，套管偏心對于水泥環內壁累積塑性應變的發展帶來了顯著的影響，加劇了井筒密封完整性失效的風險。

3.1.2 微環隙發展規律

基于式(5)～式(7)可以對累積塑性應變條件下微環隙的寬度進行計算，在此基礎上對比分析套管居中和偏心條件下微環隙產生和發展規律的差異性，量化套管偏心帶來的風險。

最大微環隙寬度隨加卸載次數發展規律如圖5所示。由圖5可知，在前5次循環加卸載條件下，加載的地應力和套管內壓一致時，套管居中和偏心條件下，微環隙寬度均較為接近，其中套管居中時水泥環微環隙呈線性變化特征，這與XI Y.等分析得到的規律較為一致[18]。套管偏心時，水泥環微環隙先保持不變(前3次循環加卸載)后呈非線性增加。該過程中套管偏心條件下產生的微環隙要小于套管居中時，但兩者整體相差較小。即便是在第3次循環加卸載兩者差異值最大時，微環隙寬度相差僅為0.60 μm。

圖5 最大微環隙寬度隨加卸載次數發展規律Fig.5 Development law of maximum micro annulus width with loading and unloading times

隨著套管內壓循環加卸載次數(≥6次)的不斷增加，套管偏心對于微環隙的影響越來越顯著。隨著循環加卸載次數(壓裂級數)的不斷增加，套管偏心條件下產生的微環隙的寬度要大于套管居中條件下，且兩者的差值在不斷地增加。當循環加卸載次數為7次時，套管居中和偏心2種條件下的微環隙寬度為15.05和16.69 μm，循環到第10次時，微環隙寬度則分別為15.81和20.50 μm。相比于套管居中初次壓裂卸載后產生的微環隙(13.22 μm)，循環加卸載10次后，套管居中條件下微環隙寬度增加19.6%，套管偏心條件下微環隙增加55.1%。

同時，結合前人的研究可知，微環隙寬度20 μm為氣竄臨界值。當套管居中時，經過10級壓裂的水泥環依然保持密封完整性，但是當套管偏心時候，在該條件下水泥環微環隙已經超過了氣竄臨界值，井筒已經發生氣竄。考慮到當前水力壓裂的級數已經超高了30級，在實際工程條件下套管偏心對于微環隙發展的影響也會更為顯著，需要在工程實際中予以考慮。

3.2 敏感性參數分析

3.2.1 偏心距

在套管應力和三維地應力的作用下，偏心距會影響水泥環在井筒中的環狀厚度分布，進而影響水泥環內壁塑性累積應變和微環隙寬度的發展。為進一步分析偏心距對于微環隙產生和發展的影響，選擇偏心角為0°、偏心距為5、10、15 mm時，套管內壓循環加卸載10次后進行計算和分析。計算結果如圖6所示。由圖6可以看出：當不存在偏心距時，受非均勻地應力的作用，水泥環塑性應變位置主要出現的水泥環內壁的兩側(累積塑性應變為0.594%)；當存在偏心距(5 mm)時，水泥環出現塑性應變的區域出現在了水泥環較厚位置的一側，微環隙主要將會在該位置產生與發展，最大累積塑性應變0.731%，相比套管居中條件下增幅為23.06%。

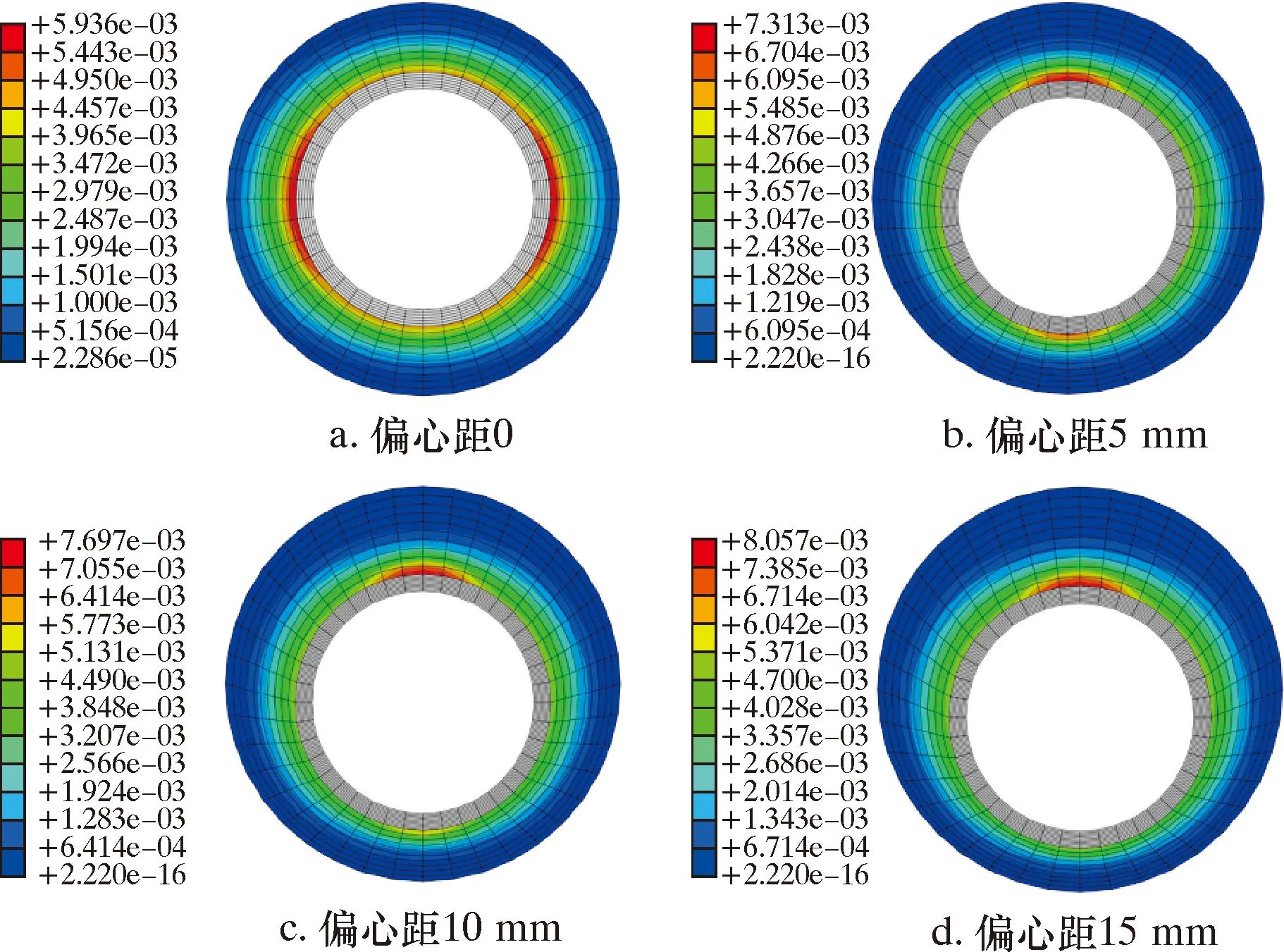
圖6 不同偏心距條件下累積塑性應變規律Fig.6 Cumulative plastic deformation law under different eccentricity conditions

隨著偏心距(10、15 mm)的不斷增加，同等加卸載次數條件下，水泥環的最大累積塑性應變不斷增加，進一步了增大微環隙產生的風險。當偏心距為15 mm時，最大累積塑性應變為0.806%，相比套管居中條件下增幅為35.69%。

基于前述結果進一步計算微環隙寬度，結果如圖7所示。當偏心距分別為5、10、15 mm時，隨著偏心距的不斷增加，微環隙寬度不斷增加，且增幅較為均勻。相比于套管居中條件下，當循環加卸載次數低于一定值時，套管偏心對微環隙產生的影響較小。但是當循環次數高于該值時，套管偏心對于微環隙寬度的影響越來越顯著，且隨著偏心距的不斷增加，微環隙相比套管居中條件下增加值越來越明顯。

圖7 不同偏心距條件下微環隙寬度發展規律Fig.7 Development law of micro annulus width under different eccentricity conditions

當循環加卸載次數為3次時，套管居中以及不同偏心距(5、10、15 mm)條件下，微環隙分別為13.89、13.00、13.29、13.70 μm；當循環加卸載次數為10次時，套管居中以及不同偏心距(5、10、15 mm)條件下，微環隙分別為15.81、19.47、20.50、21.46 μm。相比于套管居中條件下，偏心距為5、10、15 mm時微環隙增幅分別為23.15%、29.67%、35.74%。

值得一提的是，當偏心距為5 mm時，10次循環加卸載后微環隙寬度低于氣竄臨界值，但是當微環隙寬度達到10和15 mm時，就已經超過了氣竄臨界值。由此可以看出，偏心距對于井筒密封完整性影響顯著。

3.2.2 偏心角

套管偏心角的存在會改變會水泥環環狀分布特征。考慮到三維地應力的非均勻性，不同偏心角條件下套管偏心方向與最小水平主應力和垂向地應力方向的夾角會發生改變，進而影響水泥環內壁塑性應變發展規律。針對此，保持偏心距不變(10 mm)，當偏心角分別為0°、30°、60°、90°時，計算循環加卸載條件下水泥環內壁累積塑性應變，以及微環隙寬度的發展規律。

圖8為不同偏心角條件下累積塑性應變云圖。

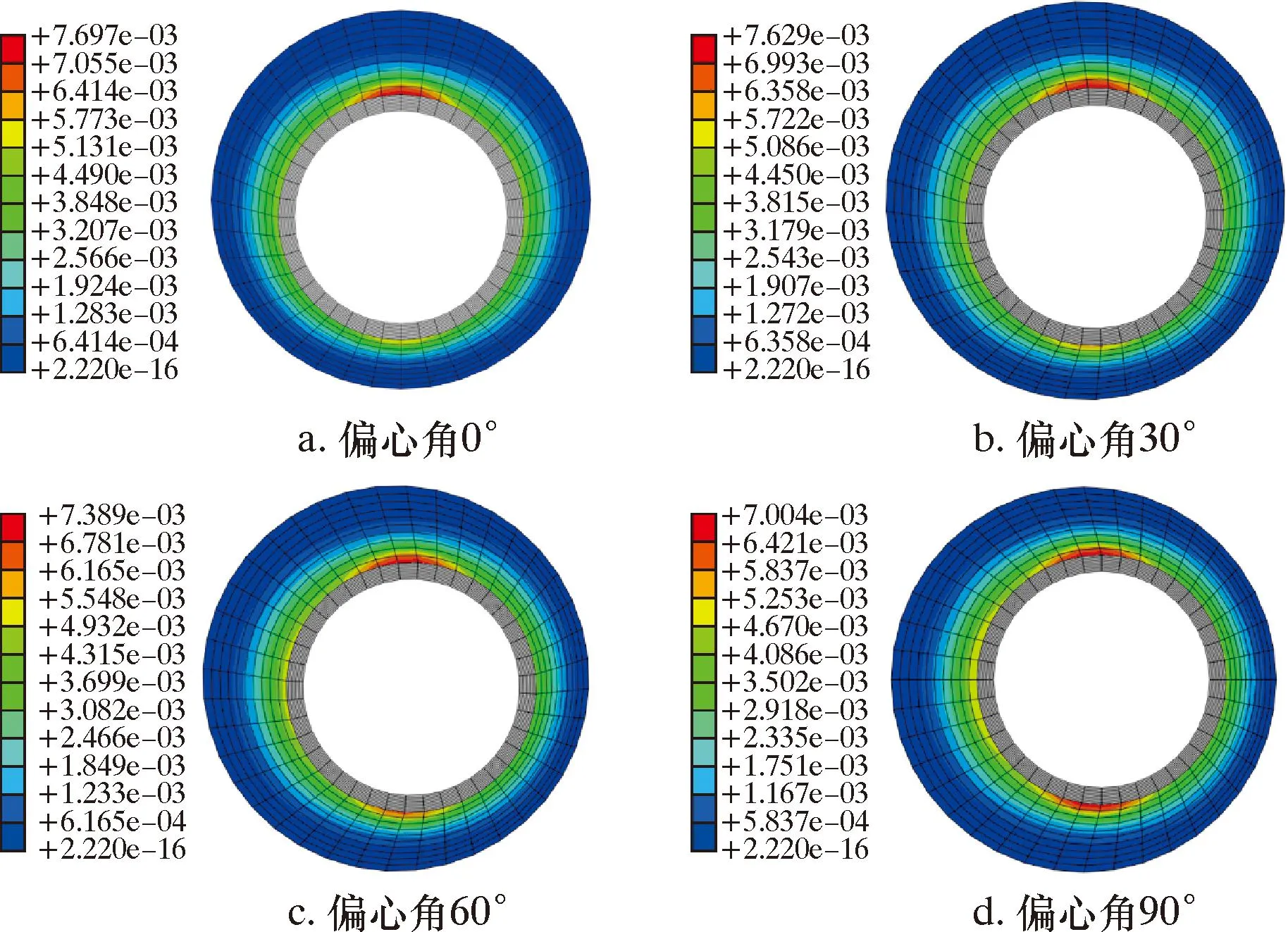
圖8 不同偏心角下累積塑性應變規律Fig.8 Cumulative plastic deformation law under different eccentric angles

由圖8可知，隨著偏心角的不斷增大，最大累積塑性應變區域發生改變。該條件下最小水平主應力小于垂向地應力，這主要是因為偏心方向與地應力夾角的方向改變導致。與此同時，在該條件下，隨著偏心角的不斷增大，同等循環加卸載條件下，累積塑性應變不斷減小。當偏心角為0°時，最大累積塑性應變為0.770%，當偏心角為90°時，最大累積塑性應變為0.700%。相比于套管居中條件下(0.594%)，累積塑性應變增長29.63%和17.84%。由此可見，偏心角對于水泥環密封完整性也帶來了顯著的影響。

基于前述計算結果計算微環隙寬度，結果如圖9所示。

圖9 不同偏心角下微環隙寬度發展規律Fig.9 Development law of micro annulus width under different eccentric angles

由圖9可以看出，當循環加卸載次數低于5次時，隨著偏心角的不斷增加，微環隙寬度不斷增加，且增速不斷減小。但在該范圍內，對于微環隙寬度的影響低于1 μm，影響較小。當循環加卸載次數超過5次時，隨著偏心角度數的不斷增大微環隙寬度不斷減小，且降速不斷增加。如前所述，套管居中條件下，循環加卸載10次后微環隙寬度為15.81 μm，當偏心角度數為0°、30°、60°、90°時，微環隙寬度分別為20.50、20.32、19.70、18.65 μm，增幅分別為29.67%、28.52%、24.60%、17.96%。

當偏心角為0°和30°時，10次循環加卸載后微環隙寬度高于氣竄臨界值。由此可以看出，偏心角對于井筒密封完整性也帶來了顯著的影響。

4 結 論

針對頁巖儲層水力壓裂過程中容易出現井筒密封完整性失效的實際，開展了循環載荷作用下套管偏心條件下微環隙產生和發展規律研究，分析了偏心距、偏心角對于微環隙產生和發展規律的影響。主要結論如下：

(1)基于水泥石損傷理論建立了套管偏心條件下累積塑性變形模型，對比分析套管居中和偏心條件下微環隙發展規律。研究結果表明，套管偏心顯著影響了微環隙的產生與發展，同等應力環境下加劇了水泥環密封完整性失效的風險。

(2)套管偏心時偏心距加速了微環隙的形成過程。當循環加卸載次數高于一定值時，相比于套管居中條件下，隨著偏心距的不斷增加，最大塑性累積應變區域發生變化，微環隙寬度不斷增加，增加了水泥環密封完整性失效的風險。

(3)當水平最小主應力低于垂向地應力時，當循環加卸載次數高于一定值時，隨著偏心角的不斷增加，微環隙寬度不斷降低，且降幅不斷增加。