基于數值模擬的新型無反饋射流振蕩元件性能影響因素研究

楊 慶

(東北師范大學環境學院)

引 言

浮選作為常見選礦方法,被廣泛應用于處理賤金屬、稀有金屬及貴金屬礦石。然而,該方法只有在處理粒度為30～70 mm礦物時,才能從原料中有效回收有價礦物,大量粒度遠小于20 mm礦物中有價值成分損失在選礦尾礦中。考慮到富礦枯竭和開發細粒級礦物的需要,亟須研發高效的細粒級礦物浮選方法[1-4]。針對細粒級礦物浮選的關鍵問題,國內外開展了大量的基礎研究,主體思路之一是:根據顆粒與氣泡的匹配性原理減小氣泡尺寸,從而改善微細粒浮選效果[5]。然而,如何以廉價且有效的方式產生微泡仍然是個難題[6]。

近年來,在氣泡生成方面的研究進展表明:微泡可以經由振蕩射流通過起泡裝置產生,振蕩射流是由穩定氣流通過一個射流振蕩器轉換而來的[7]。ZIMMERMAN等[8]研究發現,利用附壁式流體振蕩器脈動進氣的方法能夠產生高能效、大小為20～100 μm的微泡。調查發現,振蕩射流進氣方式沒有額外能量的輸入,并且射流振蕩元件無自由移動部件,具備功率小、價格優廉、能適應極端環境、壽命長等優勢[9]。

無反饋射流振蕩元件是近年新興起的一種無反饋結構的流控元件,在具有附壁式射流振蕩元件特點的同時,結構也更加簡單[10]。查閱文獻發現,國內外學者僅對無反饋射流振蕩元件基礎構型的振蕩機理、內部流場等進行了大量模擬研究,而元件優化設計和工程應用的研究相對較少[11-14]。因此,研究嘗試在無反饋射流振蕩元件基礎構型上增加分流劈,并對其不斷優化,將由圓腔出口無規則噴射而出的射流變為周期性、以正負交替方式切換方向產生的脈沖流;隨后根據分流劈模擬結果,確定形成穩定振蕩的最佳參數組合,結合文獻中模擬優化所得無反饋射流振蕩元件基礎構型的幾何參數,加工出新型無反饋射流振蕩元件,進而應用于去除金礦中二氧化硅浮選試驗。

1 模型構建

1.1 物理模型

在無反饋射流振蕩元件基礎構型的基礎上,使用機械設計軟件SolidWorks對新型無反饋射流元件進行三維建模。為了保證計算的準確性及模型更好的收斂,確保出口邊界條件可以正確設置,分流劈2個出口處增加了矩形計算域。無反饋射流振蕩元件基礎構型見圖1,新型無反饋射流元件的二維及三維圖見圖2。

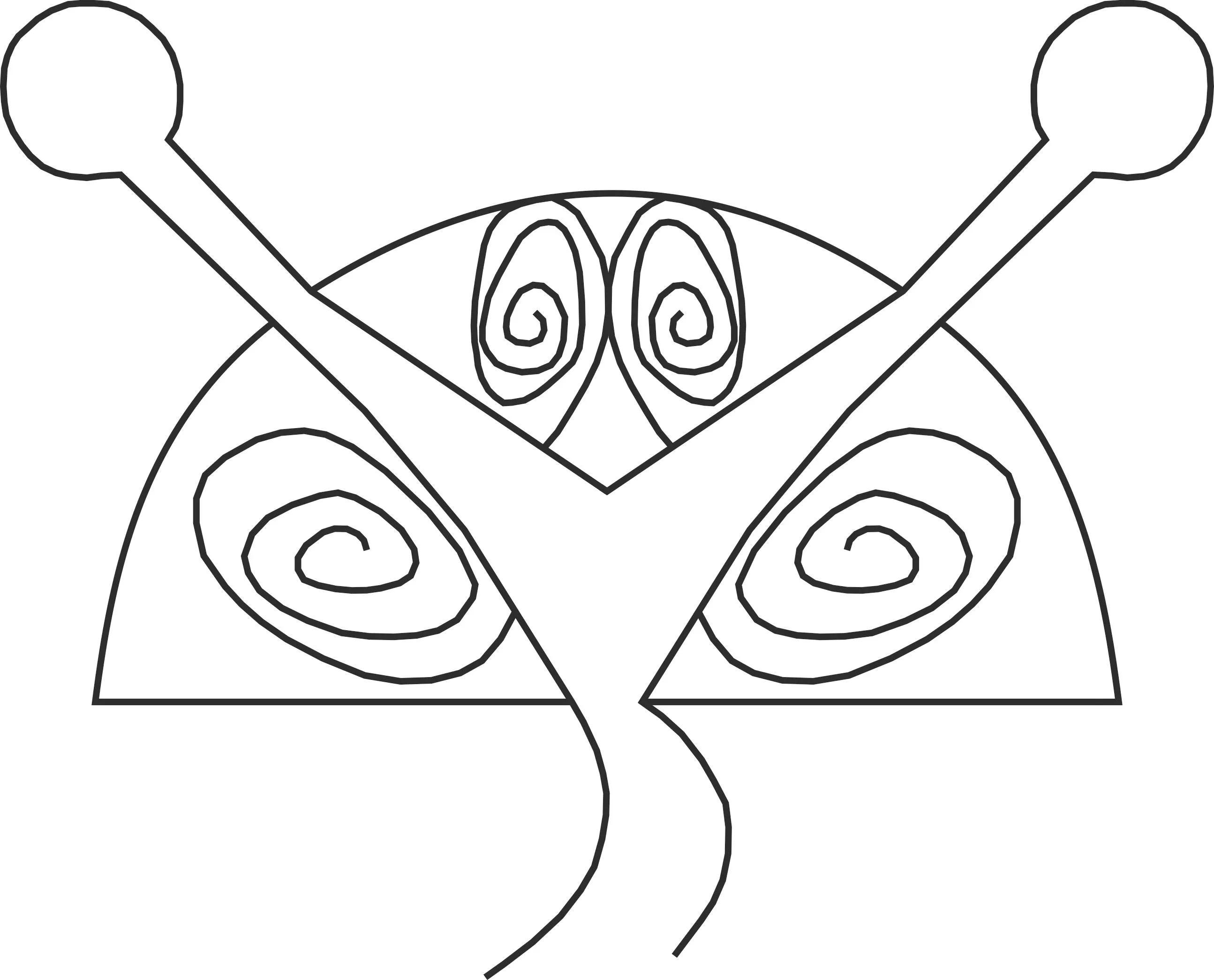
圖1 無反饋射流振蕩元件基礎構型示意圖

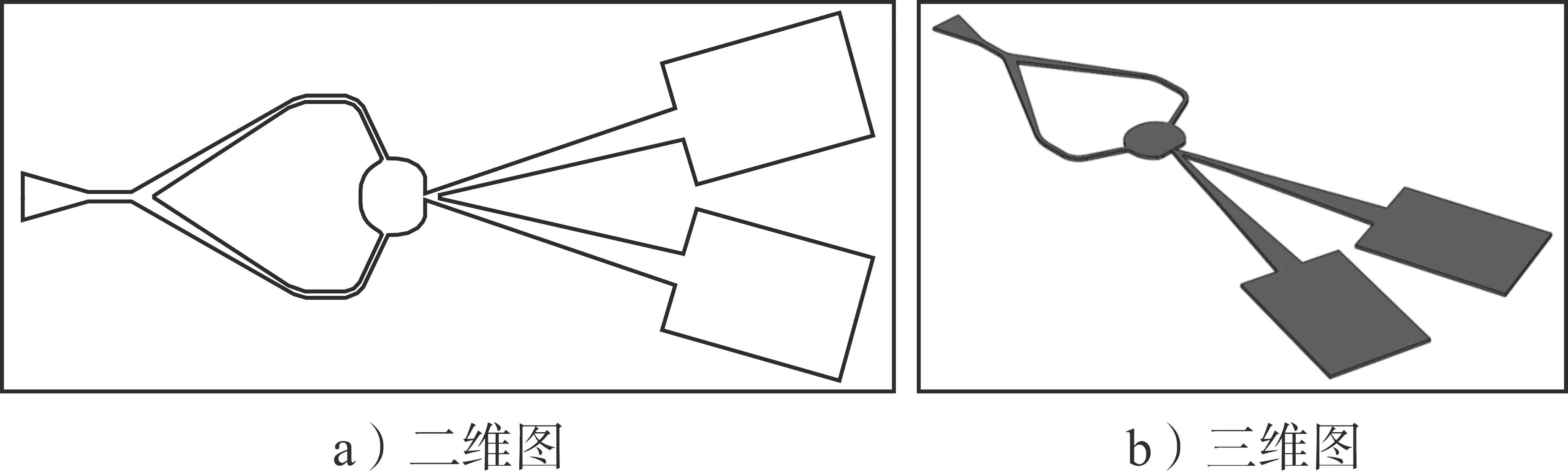
圖2 新型無反饋射流元件物理模型

本文針對新型無反饋射流振蕩元件的分流劈進行模擬優化設計,分流劈幾何尺寸見圖3。分流劈形狀為凹型,除此之外還有尖銳型與凸型,見圖4。

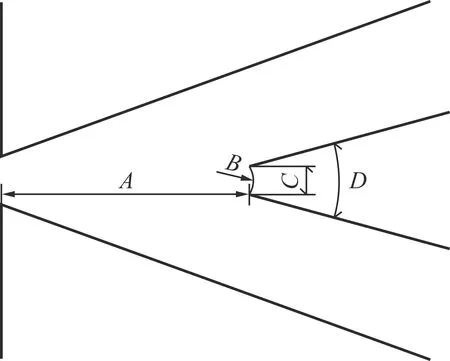
A—分流劈距離 B—分流劈半徑 C—出口管間距離 D—分流劈角度圖3 分流劈幾何尺寸示意圖

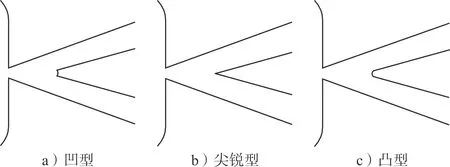
圖4 各類型分流劈形狀示意圖

1.2 控制方程

該研究的工作流體為空氣,氣流速度較大且具有壓縮性、黏性。另外,流體流動遵循流體力學中質量守恒定律、能量守恒定律與動量守恒定律。因此建立控制方程[15]。

1)連續方程(Continuity Equation):

(1)

式中:ρ為射流自身密度(kg/m);t為時間(s);u、v為速度矢量在x、y方向上的分量(m/s)。

2)動量方程(Navier-Stokes Equation)

(2)

(3)

式中:μ為動力黏度(Pa·s);Su、Sv為動量守恒方程的廣義源項。

3)能量方程(Energy Equation):

(4)

式中:T為溫度(K);Cp為比熱容(J/(kg·K));k為流體的傳熱系數;ST為流體的內熱源及由于黏性作用流體機械能轉換為熱能的部分,簡稱為黏性耗散項。

4)理想氣體狀態方程(Ideal Gas Equation):

p=ρRT

(5)

式中:p為氣體壓強(Pa);R為摩爾氣體常數(m2/(s2·K-1))。

在上述控制方程組中,有5個未知函數、5個方程,方程組封閉,可以應用ANSYS CFX19.2軟件求解和流體流動有關的物理量。

1.3 湍流模型

本文研究對象為新型無反饋射流振蕩元件,工作時其內部空氣處于高流速、非穩定狀態,因此在數值模擬過程中,選擇合適的湍流模型至關重要。對方程的直接數值模擬(DNS)由于計算量過大,目前在工程中使用較少。工程中常用基于雷諾時均法的湍流模型(RANS)及介于DNS與RANS之間的大渦模擬(LES),LES計算量較大,一般用于分析噪聲問題等。該研究采用RANS方法來進行計算。

k-ωSST湍流模型是目前計算精度較高的一種RANS模型,解決了湍流剪切應力輸運問題,可以較好捕捉壁面吸附分離等現象,適用于本研究的計算。

1.4 邊界條件與求解設置

采用瞬態計算法,總計算時長設為3 s,時間步長設定為0.000 5 s,每10步記錄一次;溫度設定為30 ℃,壁面均采用絕熱無滑移邊界;采用流速入口、壓力出口的邊界條件,流速設定為20 L/min,壓力設定為10 000 Pa;采用精度高、收斂好的有限體積離散方法進行數值計算。在分流劈出口管與出口堰交界處設置2個監測點。

1.5 網格劃分與無關性檢驗

1.5.1 網格劃分

網格劃分與生成前需要選擇網格形狀與存儲方式。由于研究的幾何模型不算復雜,為了提高精度、節省計算資源及時間,本文選擇六面體結構網格轉非結構網格的方式來離散計算域。模型整體網格劃分見圖5-a)。

圖5 新型無反饋射流振蕩元件網格劃分

提高網格質量的方式之一是對整體網格加密,但要注意,網格加密雖然可以適當提高計算精度,但網格密度過大需要占用更多的計算資源,可能造成非物理解。因此,先對整體網格加密,再根據流場需要進行局部加密,還需要注意在局部加密處與相鄰處有一定的過渡,否則網格梯度過大也會導致非物理解。在振蕩腔、圓腔內部處,由于流體碰撞激烈且流動較為敏感,需進行局部加密,其余區域采用均勻網格。局部網格加密情況見圖5-b)。

1.5.2 網格無關性檢驗

研究劃分了5種不同密度的網格,其數量梯度從38×104增加到97×104,選取2個出口管末端與矩形計算域連接處為監測點。5種不同網格數量下的監測點頻率變化見圖6。由圖6可知:頻率變化并不顯著,因此可以認為仿真模擬受網格數量的影響不大。考慮到計算資源與收斂效果,選擇50×104網格數量進行求解計算。

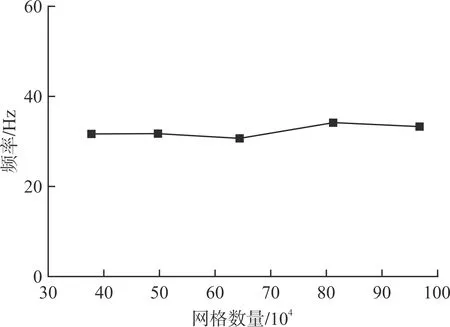
圖6 網格無關性檢驗

2 模擬結果

就元件幾何尺寸對振蕩性能的影響進行了分析,以出口頻率作為衡量指標,研究了不同幾何參數對振蕩器頻率的影響。可以產生振蕩的具體參數設置見表1。

表1 振蕩器設計幾何參數

2.1 分流劈距離

振蕩腔為分流劈、圓腔出口及周圍壁面的夾帶區,對主射流的附壁距離、振蕩性能及壓降等均有重要的影響,分流劈距離對新型無反饋射流振蕩元件振蕩性能的影響見圖7。由圖7可知:隨著分流劈距離從3.7 mm增加至4.5 mm,頻率由13.03 Hz增加至32.00 Hz;隨后繼續增加分流劈距離至4.6 mm,頻率反而減小至29.74 Hz,減少幅度約為7 %;且在分流劈距離小于3.7 mm或大于4.6 mm時不會產生振蕩。說明適當增加分流劈距離有利于提高元件的振蕩性能和雙穩特性,即易于振蕩;但隨著分流劈距離持續增加,會影響到立渦形成時間和發展,進而減少射流的切換,且分流劈距離過大會導致振蕩腔面積顯著增加,同時由于射流卷吸作用會造成能量耗散,表現為振蕩周期變長、頻率值變低。因此,在特定工況下,確定分流劈的合理位置是非常重要的。

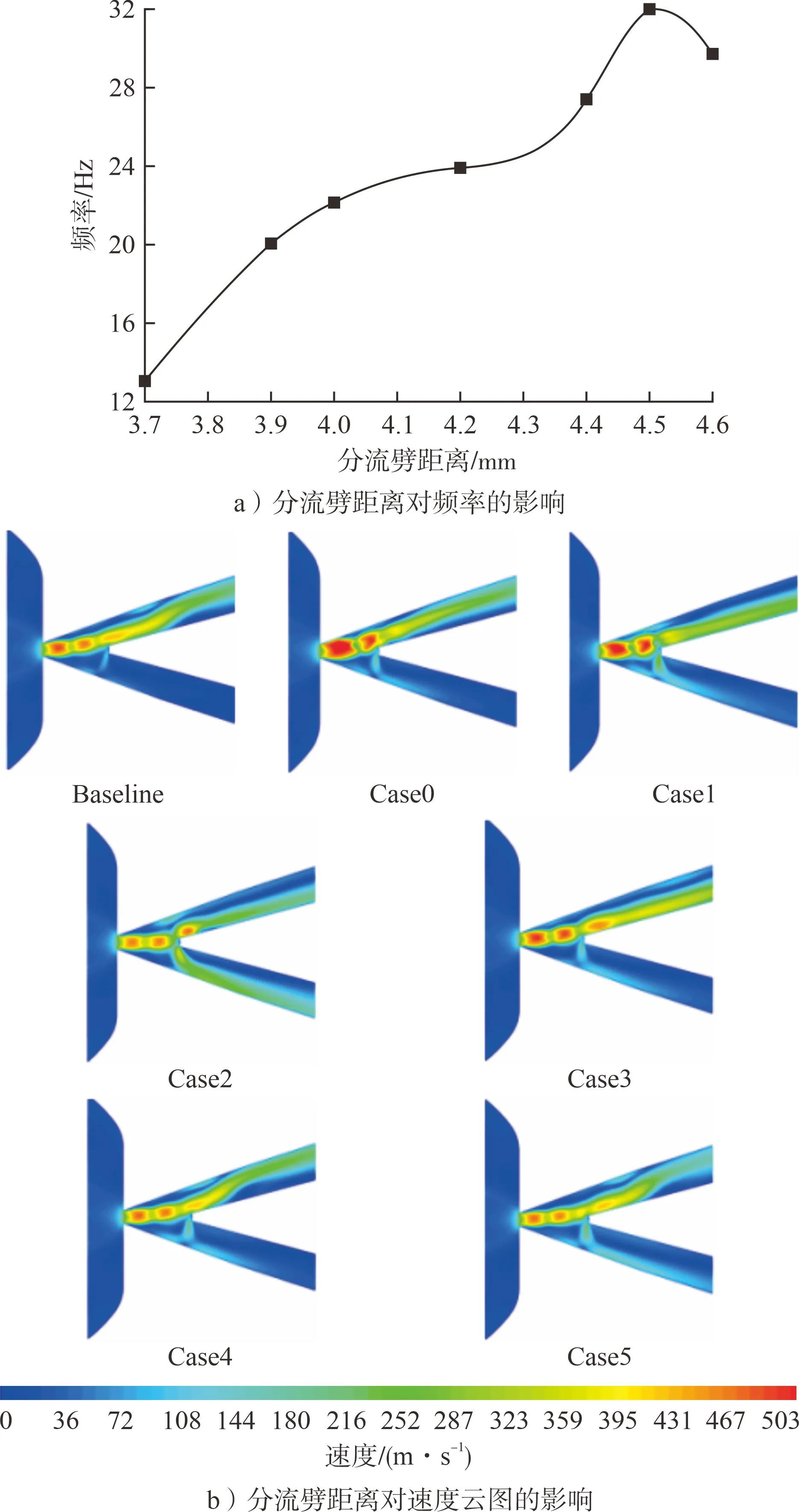
圖7 分流劈距離對新型無反饋射流振蕩元件振蕩性能的影響

2.2 分流劈半徑

分流劈半徑對新型無反饋射流振蕩元件振蕩性能的影響見圖8。由圖8可知:分流劈半徑由0.4 mm增加至0.5 mm后,頻率由22.47 Hz增加至27.39 Hz,增幅約21.90 %。說明適當增加分流劈半徑可使射流雙穩特性得到較好的保證,且易于振蕩;但隨著分流劈半徑繼續增大直至0.9 mm,頻率呈衰減趨勢,最終下降至21.16 Hz。考慮是射流附壁過程中由于卷吸作用從非附壁側進入振蕩器的氣體更多,造成能量損失增大,同時出口壓力恢復變慢,表現為頻率減小。

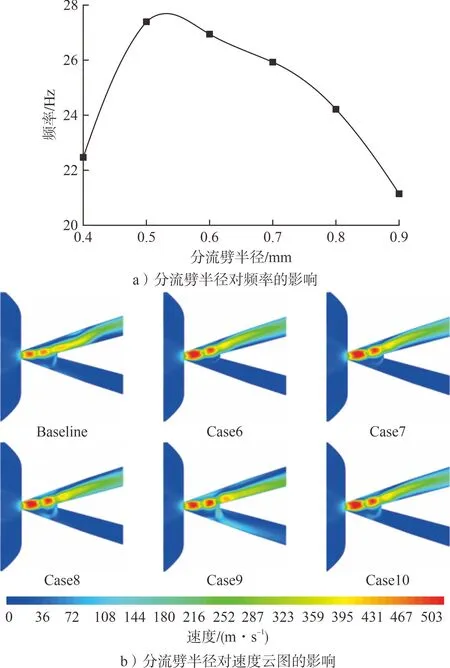
圖8 分流劈半徑對新型無反饋射流元件振蕩性能的影響

2.3 分流劈角度

分流劈角度簡稱劈角,也稱為出口管角度,指分流劈處兩側壁的夾角。分流劈角度對新型無反饋射流振蕩元件振蕩性能的影響見圖9。由圖9 可知:隨著分流劈角度增加,頻率先呈線性增長,由28°時的21.56 Hz增加至30°時的27.39 Hz,并達到最大值;之后分流劈角度與頻率呈負相關,頻率隨著分流劈角度的增加而下降,最終降至33°時的25.48 Hz。射流和側壁的碰撞區域是強湍流區,該區域需要耗散能量,而分流劈角度又會對碰撞區域湍流耗散的大小造成影響,進而影響射流總壓損失。

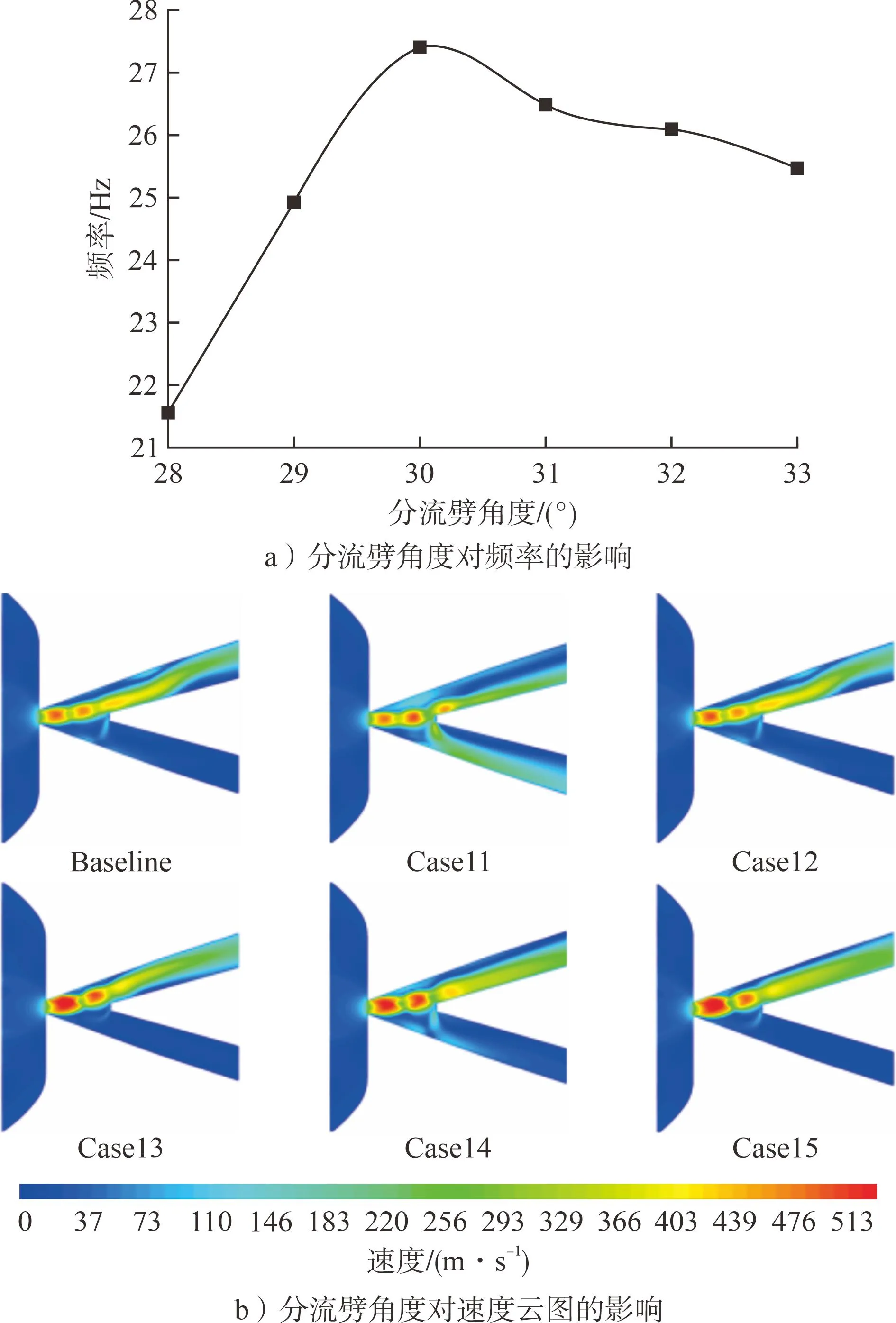
圖9 分流劈角度對新型無反饋射流振蕩元件振蕩性能的影響

2.4 出口管間距離

出口管間距離對新型無反饋射流振蕩元件振蕩性能的影響見圖10。由圖10 可知:當出口管間距離由0.3 mm增加至0.4 mm后,頻率由24.81 Hz增加至31.91 Hz,增長了28.62 %;繼續增加出口管間距離,頻率開始持續降低,直至降低至0.7 mm時的18.73 Hz。說明適當增加出口管間距離會使頻率增加,即易于振蕩;繼續增加出口管間距離,振蕩腔面積相應增加,造成主射流在射氣過程中卷吸的氣體量增加,導致壓力損失增大,表現為頻率降低。

圖10 出口管間距離對新型無反饋射流振蕩元件振蕩性能的影響

2.5 分流劈形狀

分流劈形狀對新型無反饋射流振蕩元件振蕩性能的影響見圖11。由圖11可知:不同分流劈構型下頻率表現出差異,凸型下的34.43 Hz相較于尖銳型下的31.45 Hz與凹型下的27.39 Hz有一些提升。這是因為凸型結構減少了振蕩腔的面積,致使射入的主射流氣體量減少,射流卷吸周邊流體量也減少,從而減少了能量損失。尖銳型分流劈的尖銳部分雖會造成能量損失,但振蕩腔面積仍小于凹劈。

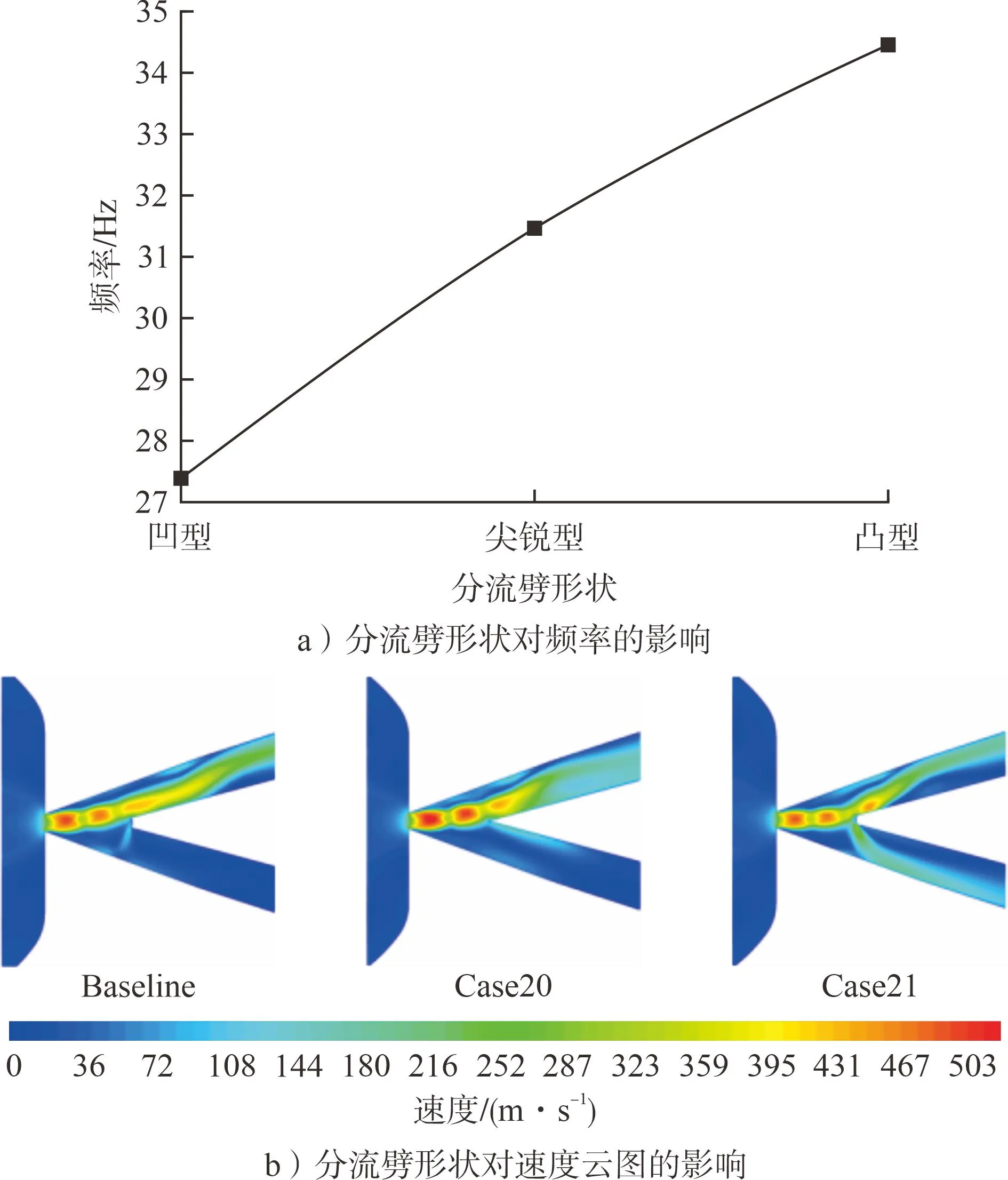
圖11 分流劈形狀對新型無反饋射流振蕩元件振蕩性能的影響

3 新型無反饋射流振蕩元件去除金礦石中二氧化硅浮選試驗

結合文獻中模擬優化所得無反饋射流振蕩元件基礎構型的幾何參數,并在上述分流劈模擬優化結果的基礎上,加工并組裝新型無反饋射流振蕩元件。選取某二氧化硅品位為79.3 %的金礦石,進行浮選試驗,對比研究使用及不使用新型無反饋射流振蕩元件浮選二氧化硅去除率。

3.1 試驗材料

某二氧化硅品位為79.3 %的金礦石;醚胺、3-(2-乙基己氧基)丙胺分別用作捕收劑和起泡劑,并且使用乙酸中和水溶液中醚胺以增加其溶解度;試驗用水均為當地自來水。

3.2 試驗設備

浮選試驗設備形象聯系圖見圖12。浮選裝置包括帶有篩網分布器(孔徑為105 μm)的柱(直徑6 cm,高150 cm)。將供液泵放在起泡器上方100 cm處的柱旁,并以一定的流速將柱底的排放物由排液泵流出,以控制礦漿-泡沫界面。微氣泡發生系統進氣方向由右至左,使用新型無反饋射流振蕩元件將空氣供應模式由穩定變為振蕩,通過由穩壓器與流量計組成的供氣控制裝置調節。為了進行比較,將虛線內裝置去除則為正常氣泡發生系統。

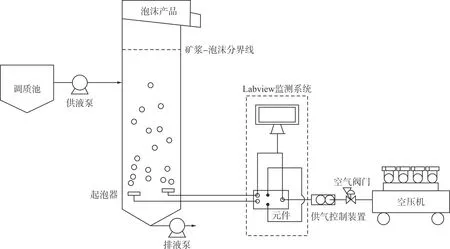
圖12 浮選試驗設備形象聯系圖

3.3 試驗結果

試驗結果顯示,對于小于10 μm的細粒二氧化硅,不使用新型無反饋射流振蕩元件穩定進氣時,浮選回收率為28.9 %;當使用新型無反饋射流振蕩元件進行振蕩進氣時,浮選回收率提高至42.2 %,增幅為46 %,大大提高了浮選回收率。

4 結 論

針對新型無反饋射流振蕩元件進行了三維模擬,得出了射流的振蕩頻率隨分流劈結構參數的變化規律,并且給出了詳細合理的描述,主要結論如下所示:

1)考察的分流劈參數包括分流劈距離、分流劈半徑、分流劈角度、出口管間角度、分流劈形狀,它們對振蕩頻率都有一定的影響。分流劈距離增加,振蕩腔容積也隨之增大,頻率呈先增加后減小趨勢,3.7 mm處為最小值13.03 Hz,并在4.5 mm處達到最大值32.00 Hz。此外,在模擬數值的上下限繼續增加或者減少分流劈距離將無明顯振蕩。將分流劈半徑自0.4 mm增加至0.9 mm,頻率呈現先增大再減小的趨勢,但是變化并不顯著。增加出口管間距離,振蕩區的面積也會增大,使得主射流在射氣過程中卷吸的氣體量增加,引發壓力損失增大,這是出口頻率降低的原因。分流劈角度的模擬優化結果表明,最高頻率為30°時的27.39 Hz,最低頻率為28°時的21.56 Hz,最大變化幅度約為27.04 %。對于不同的分流劈形狀研究表明,在相同分流劈距離下,凸型構型頻率更高,即振蕩效果更好。

2)在去除金礦石中二氧化硅浮選試驗中發現,通過使用新型無反饋射流振蕩元件將空氣供應流動模式從穩定轉換為振蕩,二氧化硅細粒級浮選回收率顯著提高,增幅為46 %。