基于迭代RMSE 法的約束阻尼板動力特性分析

劉全民，葉孝意，宋立忠，孫逸飛，劉林芽

（華東交通大學(xué)軌道交通基礎(chǔ)設(shè)施性能監(jiān)測與保障國家重點(diǎn)實(shí)驗室，江西 南昌 330013）

黏彈性阻尼結(jié)構(gòu)具有高效的減振降噪能力及質(zhì)量輕等優(yōu)點(diǎn)，廣泛應(yīng)用在航空航天、土木工程、交通運(yùn)輸?shù)阮I(lǐng)域[1-2]，如在車輪表面粘貼約束阻尼層以增大車輪阻尼[3]，在飛機(jī)壁板敷設(shè)約束阻尼層控制中低頻結(jié)構(gòu)振動和噪聲[4]等.黏彈性阻尼材料具有黏性流體和彈性固體2 種特性[5]：黏性流體在受到外力時耗散能量，而彈性固體則是儲存能量；彈性材料的應(yīng)力和應(yīng)變幾乎是同時增加和減小的，基本不存在相位差[6]；黏彈性材料的應(yīng)變滯后于應(yīng)力，應(yīng)力應(yīng)變曲線呈橢圓形，橢圓形滯回曲線所包含的面積表示黏彈性材料耗散的能量.

根據(jù)實(shí)際所需，表面敷設(shè)黏彈性阻尼結(jié)構(gòu)的形式主要有以下4 種：1）自由阻尼層結(jié)構(gòu)（FLD），直接將黏彈性材料敷設(shè)在需要減振的結(jié)構(gòu)表面上；2）被動約束阻尼層結(jié)構(gòu)（PCLD），在自由阻尼層表面再敷設(shè)一層彈性約束層；3）主動約束阻尼層結(jié)構(gòu)（ACLD），采用可控壓電材料約束層代替PCLD 中不可控約束層；4）智能約束阻尼層結(jié)構(gòu)（SCLD），將傳統(tǒng)的被動約束阻尼層與主動控制技術(shù)相結(jié)合的新興阻尼減振降噪結(jié)構(gòu)[7].被動約束阻尼結(jié)構(gòu)是一種將黏彈性阻尼材料鋪設(shè)在結(jié)構(gòu)層和具有較大剛度的約束層之間的結(jié)構(gòu)[8-9]，要求阻尼層與結(jié)構(gòu)層之間、約束層與阻尼層之間粘結(jié)牢固，阻尼層隨結(jié)構(gòu)層彎曲振動產(chǎn)生拉壓變形，同時約束層能夠約束住阻尼層的拉壓變形，從而使阻尼層產(chǎn)生剪切變形，耗散更多的振動能量實(shí)現(xiàn)減振降噪[10]，具有減振效果好、可靠性高、成本低等優(yōu)點(diǎn)，適用于鋼結(jié)構(gòu)等的振動控制.

衡量黏彈性材料耗能性能的主要指標(biāo)是材料的損耗因子，約束阻尼結(jié)構(gòu)模態(tài)損耗因子則是衡量阻尼處理是否合理、減振效果是否顯著的關(guān)鍵，不少學(xué)者對此進(jìn)行了積極的探索：郭中澤等[11]利用Reissner夾層板理論計算了約束阻尼結(jié)構(gòu)的固有頻率和模態(tài)損耗因子；Johnson 和Kienholz[12]采用模態(tài)應(yīng)變能法（MSE 法）計算了復(fù)合夾層梁前5 階模態(tài)損耗因子；Ren 和Zhao[13]采用有限元法計算了不考慮阻尼材料頻變特性時約束阻尼板前5 階模態(tài)損耗因子；Rao等[14]用直接頻率響應(yīng)技術(shù)和模態(tài)應(yīng)變能方法求解黏彈性約束阻尼梁損耗因子；Ravi 等[15-16]將黏彈性材料的力學(xué)性能參數(shù)（剪切模量和損耗因子）考慮成常數(shù)，采用有限元法建立了彈性-黏彈性復(fù)合梁動力學(xué)模型，分析了結(jié)構(gòu)前2 階固有頻率和模態(tài)損耗因子.

已有的約束阻尼結(jié)構(gòu)動力分析大多將黏彈性材料的剪切模量和損耗因子看作常數(shù)，而黏彈性阻尼材料特性隨頻率變化顯著，這將導(dǎo)致在對約束阻尼結(jié)構(gòu)動力特性進(jìn)行計算時對計算結(jié)果帶來誤差.MSE法計算效率高，較多地應(yīng)用在約束阻尼結(jié)構(gòu)模態(tài)損耗因子計算中，但已有研究往往忽略了黏彈性材料虛剛度的影響.為了減小阻尼層黏彈性材料虛剛度和參數(shù)頻變特性對約束阻尼結(jié)構(gòu)模態(tài)損耗因子計算造成的誤差，計算出的約束阻尼結(jié)構(gòu)更接近真實(shí)的模態(tài)損耗因子，本文結(jié)合修正模態(tài)應(yīng)變能法（RMSE法）和迭代算法，探討?zhàn)椥圆牧咸搫偠燃皡?shù)頻變特性對約束阻尼板的振型、固有頻率和模態(tài)損耗因子的影響.

1 模態(tài)應(yīng)變能法

模態(tài)應(yīng)變能法被認(rèn)為是黏彈性阻尼結(jié)構(gòu)模態(tài)損耗因子計算中最實(shí)用的一種方法，反映了整個結(jié)構(gòu)在敷設(shè)約束阻尼層后，每一階振型對于諧振峰的抑制作用.其主要做法是假定黏彈性阻尼結(jié)構(gòu)的模態(tài)近似于對應(yīng)結(jié)構(gòu)的無阻尼模態(tài)，有限元法計算時，只需將黏彈性阻尼材料當(dāng)作具有實(shí)剛度模量的純彈性體，從而避免了復(fù)雜的復(fù)特征值計算.該方法同時具有較高的計算效率和計算精度[17].

約束阻尼結(jié)構(gòu)形式作以下假設(shè)[18-20]：1）各層材料為線彈性、均勻、各向同性；2）結(jié)構(gòu)能正常工作，各層之間粘結(jié)非常牢固，在彎曲過程中各層之間不會產(chǎn)生滑動，將約束阻尼層整體作為一個耗能元件，不考慮能量在約束層和阻尼層之間的流動；3）垂直于板中間的各層無擠壓；4）黏彈性材料對結(jié)構(gòu)阻尼貢獻(xiàn)是主要的.

一般地，無阻尼自由振動運(yùn)動方程[21]為

式（1）的特征方程為

其中：λ 為特征值；Φ 為特征向量.

當(dāng)結(jié)構(gòu)為含有黏彈性材料的復(fù)合結(jié)構(gòu)，結(jié)構(gòu)剛度矩陣KG為復(fù)剛度矩陣，如式（3）.

式中：Ke為復(fù)合結(jié)構(gòu)彈性部分剛度矩陣；KvR為復(fù)合結(jié)構(gòu)黏彈性部分剛度矩陣實(shí)部；KvI為復(fù)合結(jié)構(gòu)黏彈性部分剛度矩陣虛部；ηv為黏彈性阻尼材料損耗因子.

黏彈性復(fù)合結(jié)構(gòu)運(yùn)動方程為

復(fù)合結(jié)構(gòu)特征方程為

式中：λG為復(fù)合結(jié)構(gòu)復(fù)特征值，如式（6）；ΦG為復(fù)合結(jié)構(gòu)復(fù)特征向量.

式中：λR、λI分別為復(fù)特征值的實(shí)部和虛部；η 為復(fù)合結(jié)構(gòu)模態(tài)損耗因子.

將式（6）代入式（5）得

將 ΦG由實(shí)特征向量 ΦR近似，則

根據(jù)式（9）兩邊實(shí)部與虛部分別相等，可得

將式（10）代入式（11），可得復(fù)合結(jié)構(gòu)模態(tài)損耗因子的計算表達(dá)式為

聯(lián)合式（13）、（14）可得

2 基于迭代的RMSE 算法

本文采用基于RMSE 的迭代算法求解復(fù)合結(jié)構(gòu)的頻率和損耗因子有以下2 個原因：1）一般而言，約束阻尼結(jié)構(gòu)不同階次下模態(tài)損耗因子不同，不同階次采用相同修正系數(shù)可能導(dǎo)致修正不足或過量；2）黏彈性材料的剪切模量及損耗因子隨頻率變化較大，這使得不同模態(tài)階次下剪切模量、材料損耗因子具有顯著差異，這對模態(tài)損耗因子和固有頻率的計算有很大影響.RMSE 方法僅在計算特征向量時使用復(fù)剛度的絕對值來考慮虛剛度的影響，從而避免特征向量和剛度雙重修正引起的過度修正.黏彈性材料參數(shù)是頻變的，而約束阻尼結(jié)構(gòu)的固有頻率又與材料參數(shù)有關(guān)，而這可以通過迭代算法來實(shí)現(xiàn).通過迭代計算考慮黏彈性阻尼材料的頻變特性，可更準(zhǔn)確地分析模態(tài)損耗因子和固有頻率.

該迭代法的具體實(shí)現(xiàn)步驟：

步驟1約束阻尼結(jié)構(gòu)進(jìn)行實(shí)模態(tài)分析得各階固有頻率.

步驟2選取該頻率下阻尼層材料損耗因子和剪切模量，進(jìn)行模態(tài)分析得到新的固有頻率.

步驟3將前、后2 組的固有頻率進(jìn)行比較，若滿足誤差公式（其中，fi,j為第j次模態(tài)分析后約束阻尼結(jié)構(gòu)的第i階頻率），則輸出固有頻率，并采用RMSE 方法計算該階模態(tài)損耗因子，否則，重復(fù)步驟1 和步驟2.

3 計算方法驗證

為驗證本文提出的基于RMSE 的迭代法較MSE 迭代法的準(zhǔn)確性，建立與文獻(xiàn)[23]相同的模型，計算結(jié)構(gòu)固有頻率和模態(tài)損耗因子，并與MSE 迭代法及文獻(xiàn)[23]的模態(tài)試驗測試數(shù)據(jù)對比分析.本文RMSE 迭代法考慮了阻尼層虛剛度的貢獻(xiàn)，這與已有MSE 迭代法顯著不同.

文獻(xiàn)[23]試驗材料為ZN-3 黏彈性阻尼材料，試驗的頻率范圍為0.1～200.0 Hz，且在該范圍內(nèi)材料的儲能模量E和損耗因子 ηv、頻率f的關(guān)系為

文獻(xiàn)[23]中試驗采用的結(jié)構(gòu)形式是一邊固定的約束阻尼板.本文均采用實(shí)體單元模擬結(jié)構(gòu)層、約束層和阻尼層，計算模型邊界條件為懸臂約束，如圖1所示.基層和約束層彈性模量均為70 GPa，模型其他參數(shù)如表1 所示，計算結(jié)果對比如表2 所示.

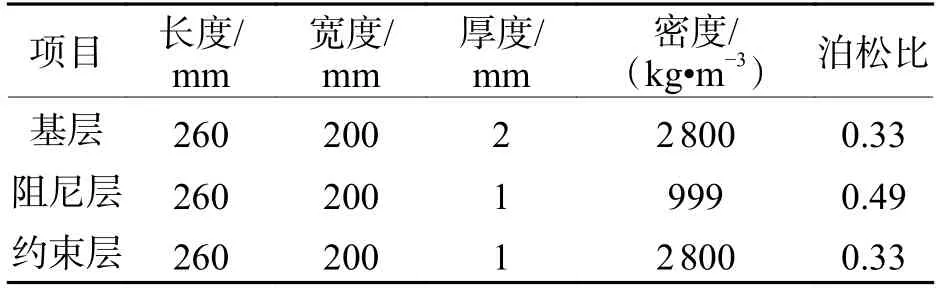
表1 文獻(xiàn)[23]模型參數(shù)Tab.1 Model parameters in reference [23]

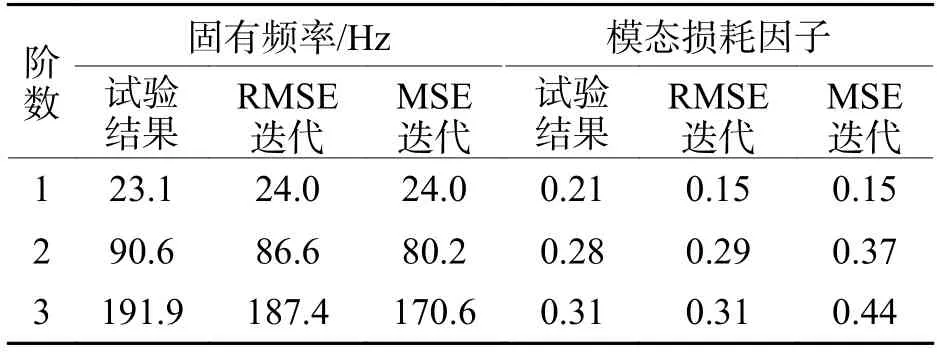
表2 試驗與計算結(jié)果比較Tab.2 Comparison of experimental and calculated results

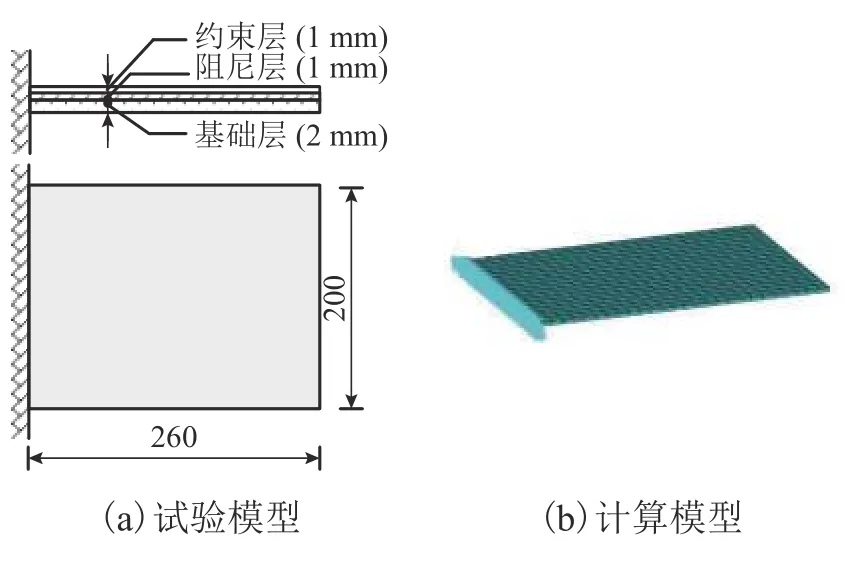
圖1 結(jié)構(gòu)模型Fig.1 Structural model

從表2 中可以看出，對比文獻(xiàn)[23]的實(shí)測數(shù)據(jù)，本文算法考慮阻尼層虛剛度貢獻(xiàn)和材料頻變特性后得到的固有頻率和模態(tài)損耗因子誤差更小，表明本文提出的算法較傳統(tǒng)MSE 迭代法的計算精度更高.由于本文算法涉及的仍然是與傳統(tǒng)MSE 法相同的實(shí)特征求解，通常迭代3～5 次計算結(jié)果即可收斂，計算效率雖低于傳統(tǒng)MSE 法，但仍然明顯高于復(fù)特征值法.

4 約束阻尼板動力特性分析

黏彈性阻尼材料的損耗因子和儲能剪切模量隨頻率變化顯著.本文選用ISD-112 型黏彈性阻尼材料，頻變儲能剪切模量和材料損耗因子如圖2.在0～1 000.0 Hz 內(nèi)，儲能剪切模量G和損耗因子ηv與頻率f的關(guān)系[1]為

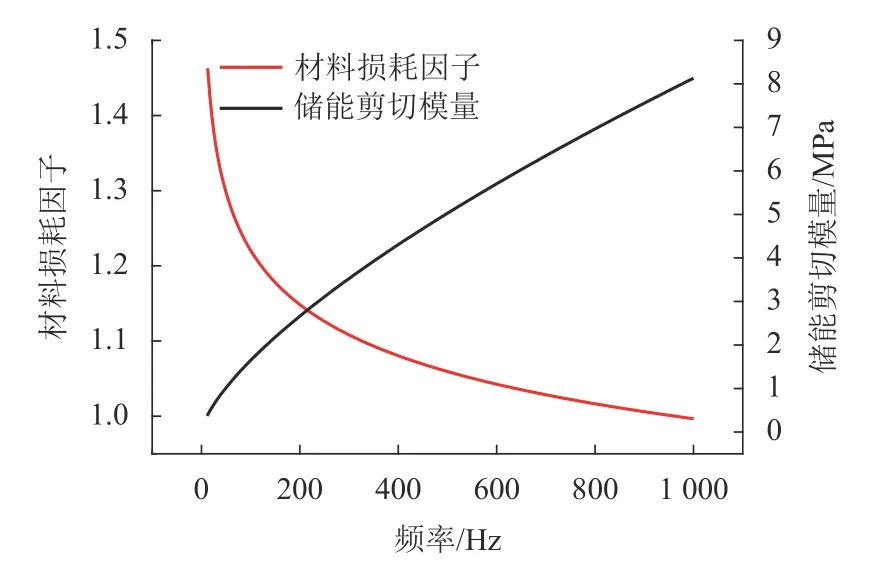
圖2 ISD-112 阻尼材料頻變特性Fig.2 Frequency-dependent characteristics of damping material ISD-112

在采用迭代算法計算約束阻尼板模態(tài)損耗因子時，利用式（18）、（19）可得到任意頻率下阻尼材料的儲能剪切模量和材料損耗因子.

計算模型邊界條件為四邊簡支，基層和約束層彈性模量為68.95 GPa，其他具體物理參數(shù)如表3 所示.

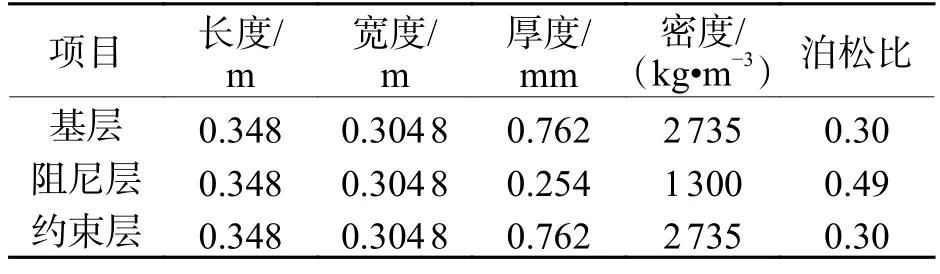
表3 模型參數(shù)Tab.3 Model parameters

4.1 模態(tài)振型對比

由于本文關(guān)心的頻率范圍是0～1.0 kHz，所以選取中間頻率500.0 Hz 對應(yīng)的儲能剪切模量和材料損耗因子作為約束阻尼板非頻變參數(shù)進(jìn)行模態(tài)分析.迭代法則可以選擇任意頻率下的儲能剪切模量和材料損耗因子作為初值，按照第2 節(jié)描述的步驟進(jìn)行迭代模態(tài)分析.

迭代前后計算所得的前20 階模態(tài)振型相差不大，現(xiàn)取其中的4 階計算結(jié)果進(jìn)行對比分析.約束阻尼板結(jié)構(gòu)層第1、12、15、20 階模態(tài)振型結(jié)果如圖3 所示.

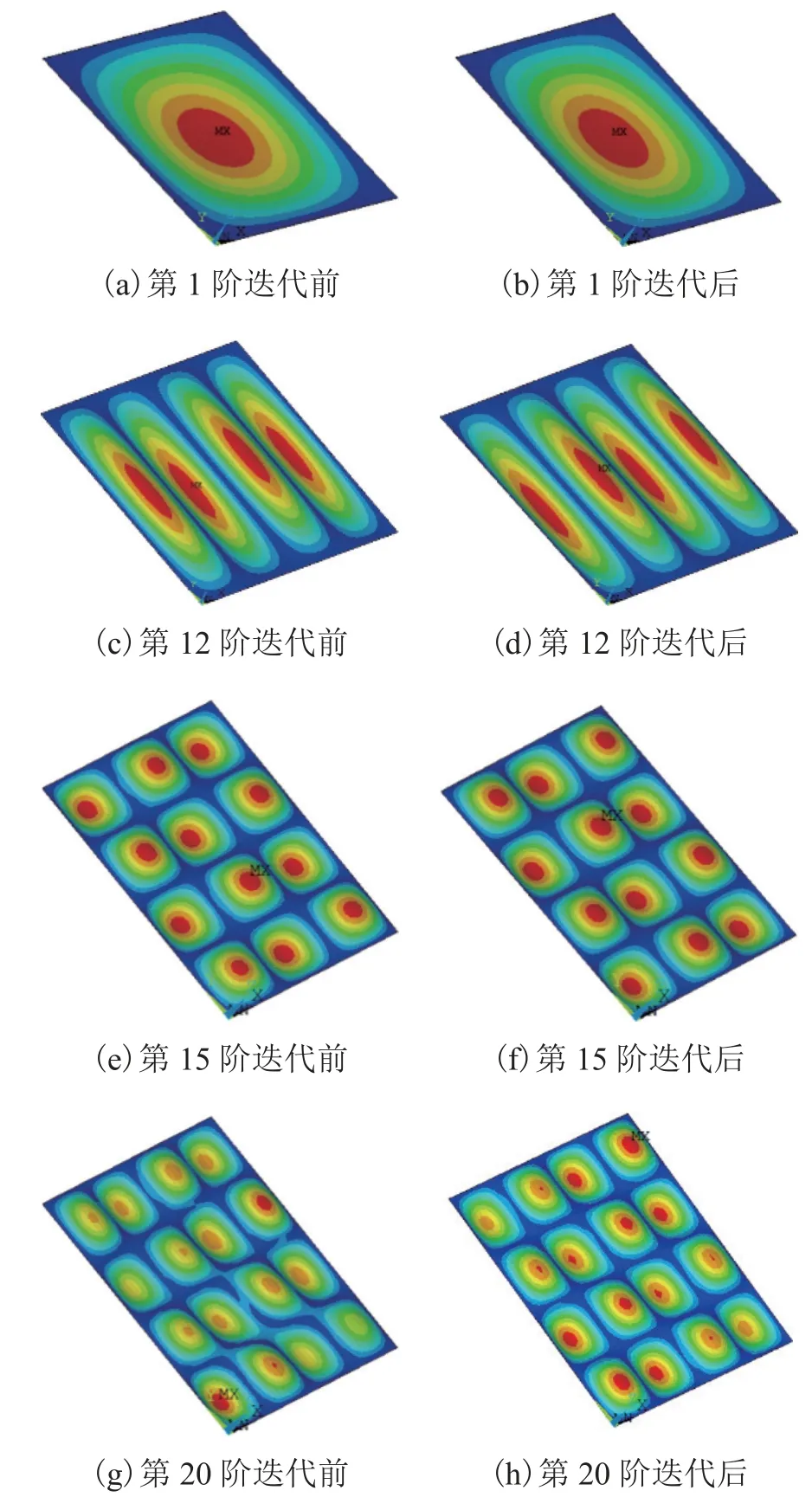
圖3 結(jié)構(gòu)層模態(tài)振型Fig.3 Modal shapes of structural layer

從圖3 可以看出：迭代前后，各階模態(tài)振型形狀基本相同，僅部分模態(tài)振型相位相差180°.這是由于阻尼層對整個結(jié)構(gòu)的剛度貢獻(xiàn)不大，所以剪切模量的改變對振型形狀的影響可忽略，但會改變振型的相位.

4.2 固有頻率對比

迭代前后黏彈性約束阻尼板前20 階固有頻率計算結(jié)果如圖4 所示.由圖可見：對于前10 階，非迭代計算的固有頻率均高于迭代后的，且差值逐漸減小；對于后10 階，非迭代計算的固有頻率又低于迭代后的結(jié)果，且差值逐漸增大；在第10 階時，由于該頻率下的阻尼層剪切模量與實(shí)際值最為接近，故迭代前后的差值最小.

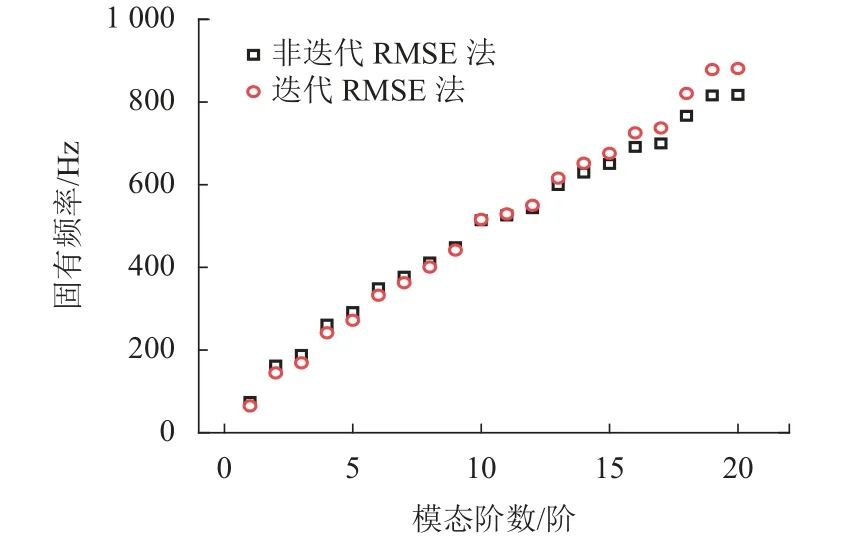
圖4 迭代前后各階固有頻率對比Fig.4 Comparison of intrinsic frequencies before and after iteration

迭代前后，約束阻尼結(jié)構(gòu)的質(zhì)量矩陣不發(fā)生改變，對于影響固有頻率的因素而言，唯一的變化在于結(jié)構(gòu)的剛度.迭代前后剛度的不同是阻尼層剪切模量變化引起的，阻尼材料的剪切模量隨頻率變化函數(shù)如式（18）所示，阻尼層剪切模量隨頻率增大而增大，所以迭代法計算時，結(jié)構(gòu)剛度隨階數(shù)增大而增大.非迭代計算，阻尼層剪切模量只能取定值（本文取500.0 Hz 對應(yīng)的剪切模量），結(jié)構(gòu)剛度矩陣不變，顯然低階模態(tài)高估了阻尼層剪切模量，高階模態(tài)又低估了阻尼層剪切模量.

以上分析表明，忽略阻尼層材料虛剛度貢獻(xiàn)及其頻變特性，阻尼層模量取定值會造成固有頻率計算出現(xiàn)明顯偏差.

4.3 模態(tài)損耗因子對比

為了修正由于未考慮黏彈性材料頻變特性而引起的誤差，Johnson 等[12]提出了利用頻率函數(shù)f(ω)對損耗因子進(jìn)行修正，損耗因子修正計算公式為

式中:ω為圓頻率；ωi為第i階模態(tài)頻率；Gd(ωi) 為第i階模態(tài)對應(yīng)的黏彈性材料剪切模量；Gd,ref為實(shí)模態(tài)分析中采用的剪切模量；ηi為第i階非迭代模態(tài)損耗因子；ηr為修正模態(tài)損耗因子.

將采用頻率修正法計算得到的模態(tài)損耗因子與迭代前后的模態(tài)損耗因子進(jìn)行對比，如圖5 所示.可以看出，非迭代計算的模態(tài)損耗因子在低頻時偏差較大，頻率修正法計算的模態(tài)損耗因子在高頻時偏差較大.

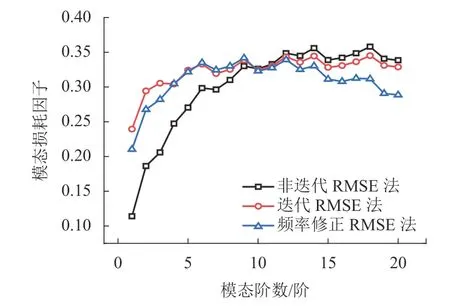
圖5 模態(tài)損耗因子對比Fig.5 Comparison of modal loss factors

將迭代法計算結(jié)果作為參照，對比分析不進(jìn)行迭代和頻率修正對模態(tài)損耗因子的影響.不進(jìn)行迭代的計算誤差范圍為-56.00%～3.72%，對于頻率修正后的計算誤差范圍為-10.20%～3.62%.所以通過頻率修正能在一定程度減小損耗因子的計算誤差，但在高階時會導(dǎo)致修正過度，說明頻率修正得到的損耗因子也存在較大誤差，不能較好地解決不考慮阻尼材料頻變特性帶來的影響.

3 種方式下求得的模態(tài)損耗因子在第10 階最為接近，原因是第10 階時結(jié)構(gòu)頻率在500.0 Hz 左右，而不進(jìn)行迭代采用的材料參數(shù)為頻率500.0 Hz對應(yīng)的材料屬性值，所以在該頻段附近的計算結(jié)果會比較接近真實(shí)值，才會出現(xiàn)三者的計算結(jié)果相近.

4.4 約束阻尼層參數(shù)分析

阻尼層厚度和約束層厚度對約束阻尼板減振效果至關(guān)重要，所以本節(jié)主要分析這2 個參數(shù)對約束阻尼結(jié)構(gòu)的模態(tài)損耗因子的影響規(guī)律.

4.4.1 阻尼層厚度對比分析

將約束層厚度取0.762 mm，阻尼層的厚度依次取0.154、0.254、0.354、0.454、0.554 mm，討論在不同厚度下約束阻尼板模態(tài)損耗因子的變化，計算結(jié)果如圖6 所示.由此可見，隨著阻尼層厚度的增加，損耗因子不斷增大，但增加相同的厚度，損耗因子增量不斷減小.

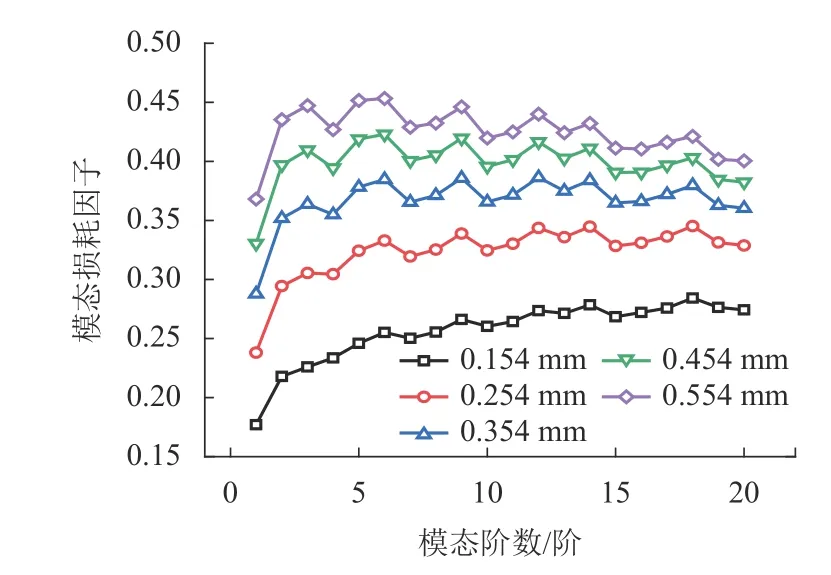
圖6 不同阻尼層厚度下CLD 板模態(tài)損耗因子Fig.6 Modal loss factors of CLD plate under various thicknesses of damping layer

4.4.2 約束層厚度對比分析

阻尼層厚度取0.254 mm，約束層的厚度依次取0.262、0.562、0.762、1.262、1.762 mm 和2.262 mm，討論在不同厚度下約束阻尼結(jié)構(gòu)模態(tài)損耗因子變化，計算結(jié)果如圖7 所示.由此可見，隨著約束層厚度增加，結(jié)構(gòu)模態(tài)損耗因子不斷增大，但增大到一定值時，開始減小.這說明并不是約束層厚度越大越好，而是存在最佳值使模態(tài)損耗因子最大.約束層厚度與基層厚度相等時，模態(tài)損耗因子最大.

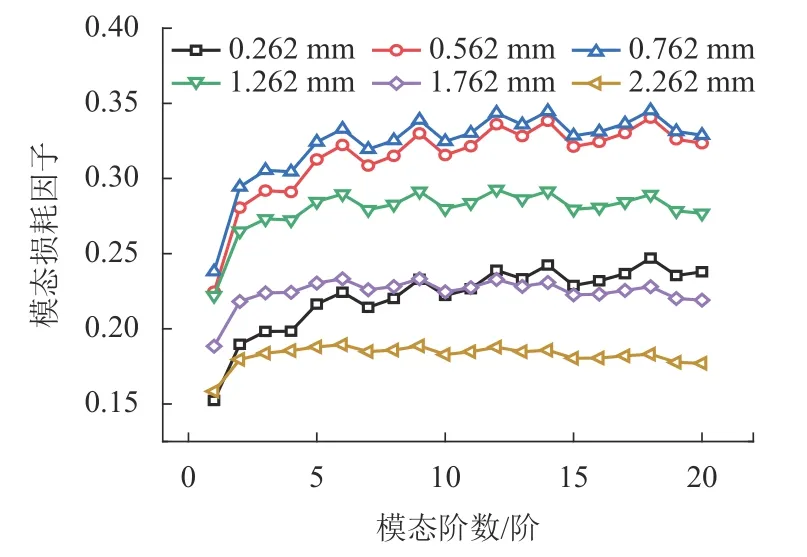
圖7 不同約束層厚度下CLD 板模態(tài)損耗因子Fig.7 Modal loss factors of CLD plate under various thicknesses of constraint layer

5 結(jié)論

1）通過與相關(guān)文獻(xiàn)試驗實(shí)測數(shù)據(jù)對比驗證了本文所提出算法的準(zhǔn)確性，并且較已有MSE 迭代法具有更高的計算精度，說明有必要考慮阻尼層虛剛度的貢獻(xiàn).

2）不考慮阻尼材料參數(shù)頻變特性，結(jié)構(gòu)層模態(tài)振型形狀基本不變，但部分模態(tài)的振型相位相反.

3）對于本文選取的阻尼材料而言，阻尼層剪切模量取中間頻段值會造成固有頻率在低階模態(tài)時計算結(jié)果偏大，在高階模態(tài)時偏小.

4）不考慮阻尼材料參數(shù)頻變特性計算得到的模態(tài)損耗因子只有在中間頻段處較為準(zhǔn)確，其他頻段處有較大誤差，特別是低階模態(tài)對應(yīng)頻段.

5）在一定范圍內(nèi)，結(jié)構(gòu)損耗因子與阻尼層厚度成正比.對約束層而言，其厚度與基層厚度相等時，結(jié)構(gòu)模態(tài)損耗因子最大.