緩傾斜厚大礦體采場結構參數優化研究與應用

柴 紅 郭俊超 楊淑慧 劉成博

(1.黃河水利職業技術學院土木與交通工程學院,河南 開封 475004;2.鄭州大學水利與土木工程學院,河南 鄭州 450001;3.山西省第三地質工程勘察院有限公司,山西 晉中 030620)

在礦山實際生產過程中,采場結構布置參數優化必須從經濟效益和安全條件兩個方面考慮。 良好的結構布置方案不僅能夠提升礦石的采出率、提高采出礦石的品位,而且能夠有效地保證礦柱、礦房內施工安全。 礦山的安全與經濟效益是礦山設計的核心要義,因此,礦山設計過程中,根據實際情況確定與優化采場結構參數就顯得尤為重要。

近年來,國內外諸多學者對采場結構參數優化進行了深入研究[1-4]。 目前,常用的確定采場結構參數的方法主要有經驗類比法[5]、數值模擬分析法[6-9]、理論分析法[9-10]等。 劉澤洲等[11]基于查表法確定了厚大礦體的采場寬度,并利用經驗方法與數值模擬方法對采場參數進行了優化。 焦國芮等[12]、羅來和等[13]設計了采場結構參數方案,應用FLAC3D軟件進行數值模擬,探究了采場結構參數合理取值。 周寶坤等[14]為了提高礦石品位,利用響應面法對礦房參數進行了優化。 陳順滿等[15]為了取獲最優的采場結構參數,采用中心復合試驗研究了采場高度、礦柱直徑、礦柱排距和礦柱間距對破碎圍巖條件下的礦柱最大拉應力、最大壓應力和礦石回收率的影響規律。 徐帥等[16]運用SOM 模型,設計了多水平參數試驗,并通過數值模擬軟件,實現了擴展方案的正向預測、結構參數反向預測以及影響采場穩定性的主因素分析。張亞偉等[17]根據礦山實際情況,利用三維有限元動態仿真模擬方法對采場結構及推進方向進行了優化分析。 蘭明等[18]基于彈性力學理論,建立了板狀結構力學模型,分析了厚板結構發生變化時所對應的拉應力變化特征,確定了階段嗣后充填采場最優開采參數,并通過多因素分析法對理論計算結果進行了驗證。

本研究以山東半島地區某地下礦為例,將Mathew 穩定圖表法與數值模擬計算方法相結合,首先利用經驗分析法綜合考量采場的安全性與經濟性,對采場尺寸參數進行預估;然后基于FLAC3D數值模擬軟件,以礦柱垂直應力、頂板拉應力與頂板位移為研究對象,對采場參數取值進行進一步分析,在此基礎上,綜合經濟、技術因素確定最優采場結構參數。

1 工程概況

山東半島某地下礦所開采的某礦段中富含了大量的金、鎢、銅等多種金屬礦體,開采段長約143 m,傾向長度為128～186 m,厚度為18.7～36.8 m,平均24.8 m。 礦體上盤為花崗巖,普氏系數f為13～18;下盤為大理巖,普氏系數f為10～14;礦體較為致密且相對堅硬,普氏系數f為9。

礦塊沿礦體走向方向布置,由于礦塊在中間位置存在一定的夾矸,降低了礦石品位,因此在礦段中間位置、北偏東12°方向設置了寬19 m 的永久性保護礦柱(圖1)。 開采順序分為兩個階段進行,首先是回采礦柱,待回采完畢后進行充填;其次是礦房回采,回采后再次進行充填。 根據設計,礦柱寬度為16 m,左右兩個盤區的走向長度為62 m,礦房寬度(即礦房的傾斜長度)需要進一步確定。 采場礦房寬度越大將會導致整個采場的懸頂面積增大,礦柱的穩定性與頂部圍巖的穩定性將同時減弱,因此本研究通過進一步分析給出合理的礦房寬度取值。 采礦方案如圖1所示。

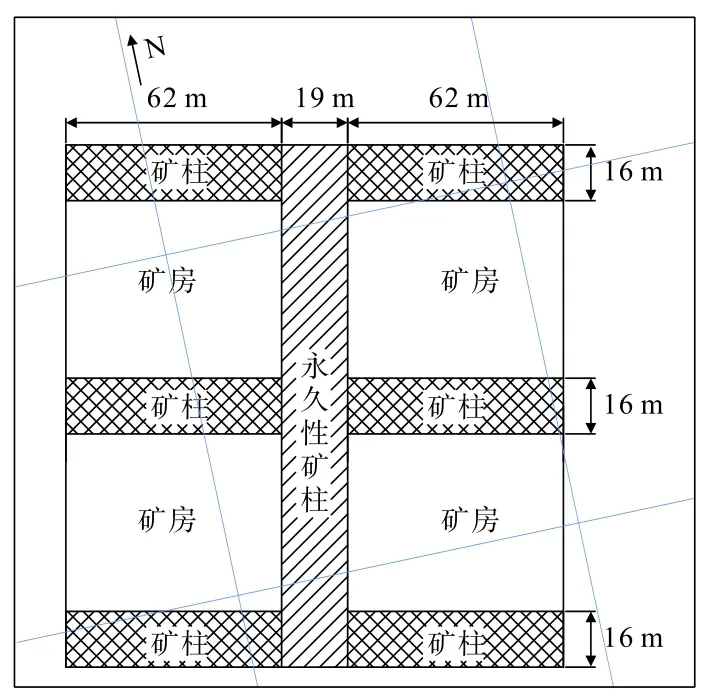
圖1 礦塊開采尺寸Fig.1 Mining size of ore blocks

2 基于Mathew 穩定圖表法的礦房寬度確定

Mathew 穩定圖表法是由英國Golder 公司工程人員MATHEW 提出的,在判斷采場穩定性方面,是目前應用較為廣泛的方法之一。 其基本思想為綜合考慮采場的巖石力學性質和開采技術因素經驗性確定采場的穩定性情況。 隨后POTVIN 基于工程實例對Mathew 穩定性圖表進行了發展,得到新的Mathew 穩定性圖表,如圖2 所示。 圖2 中橫坐標為采場暴露面形狀系數S,縱坐標為巖體穩定性指數N,通過現場確定的采場尺寸和穩定性系數,從而可以確定坐標點位置,據此判斷采場的穩定性。 其中,穩定性區域分為3 類,即穩定區、不穩定區和崩落區。 因此,在確定采場區域時,根據采場穩定性系數N,可以反算出穩定情況下的采場尺寸。

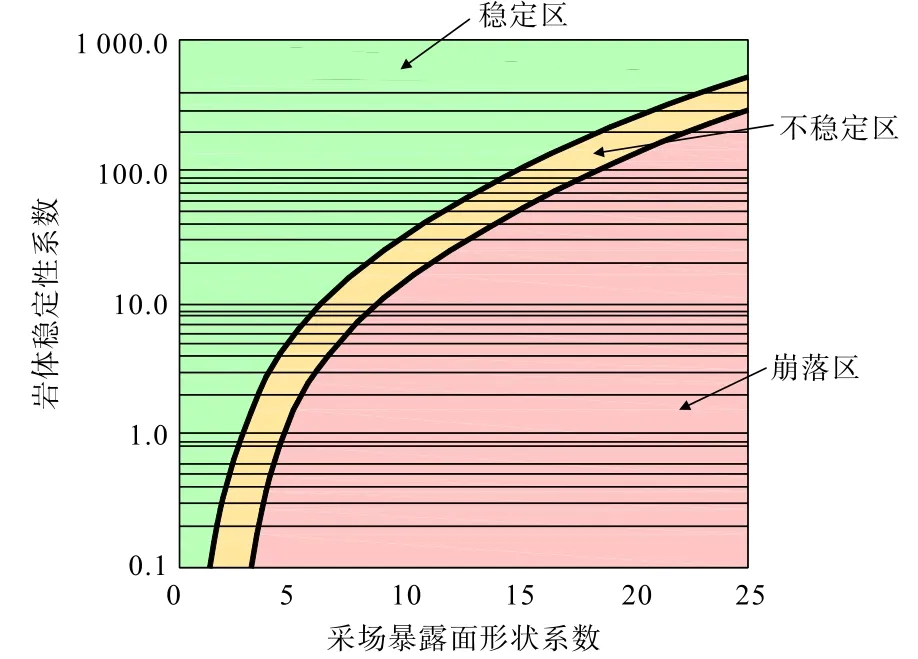
圖2 基于Mathew 穩定圖表法的采場穩定性區域劃分Fig.2 Regional division of stope stability based on Mathew stability chart method

2.1 基于Mathew 方法確定礦房寬度

2.1.1 穩定性指數N 確定

穩定性指數N可進行如下計算:

式中,Q為巖體質量指數,綜合考慮了巖石的力學特性、所處的應力場以及巖體的空間關系;A為巖石應力系數,與采場所受的應力有關;B為巖體缺陷方位修正系數,綜合考慮了巖體中的缺陷,例如弱面、節理、孔洞等影響;C為巖石暴露的修正系數,與采場暴露情況有關。

巖體質量指數Q計算公式為

式中,R為巖體質量指標,即RQD(Rock Quality Designation),表示巖體良好度的指標;Jr為節理粗糙度系數,表征節理面形貌;Jw為節理裂隙水折減系數,表征節理裂隙水對節理的影響;Ja為節理蝕變、充填及膠結程度系數,表征節理初始狀態的膠結程度;Jn為節理組數;Sf為應力折減系數。

巖石應力系數A綜合表征了兩個方面因素:① 外在因素,由于礦石開采導致的應力場重新分布形成應力集中;② 內在因素,巖石自身的單軸抗壓強度對應力系數A的影響。

巖體缺陷方位修正系數B綜合反映了頂板方位對穩定性的影響,其表達式為

式中,φ為頂板傾角,(°)。

對于巖石暴露的修正系數C,在水平情況下,C=1;其他情況下,取值為

式中,α為暴露面與水平方向的夾角,(°)。

2.1.2 采場形狀系數S

形狀系數S是主要表征暴露面形貌特征的參數,一般情況下采場為矩形,主要參數為矩形的長和寬。S值可進行如下計算:

式中,L1為采場長度,m;L2為采場寬度,m。

2.2 采場尺寸確定

根據上述關于穩定性指數N和采場形狀系數S計算過程的描述,此時根據采場的空間力學特性能夠計算得到穩定性指數N,在此基礎上,判斷出穩定區、不穩定區以及崩落區的范圍。 由于設計過程中采場長度固定,因此通過S值能夠確定采場寬度。 基于采場的圍巖力學性質與應力特征,根據式(1)至式(4)得到穩定性指數N與計算參數取值,見表1。

表1 計算參數取值Table 1 Values of calculation parameters

根據確定的穩定性系數N取值,并根據圖2 可知,若采場處于穩定區,此時形狀系數S為0～9.73;若采場處于不穩定區,S為9.73～12.55;若采場處于崩落區,S為12.55～25。

為防止采場崩落,在局部支護的情況下,S為9.73～12.55,既保證了安全,同時確保達到較高的產量,因此由式(6)計算得到的采場寬度L2為28.36～42.17 m。

式中,根據采場設計參數,L1取62 m。

3 數值模擬計算

3.1 模擬方案

基于Mathew 穩定圖表法確定的采場寬度為28.36～42.17 m,在保證礦柱寬度為19 m、采場長度為62 m 的前提下,進一步對采場寬度參數取值進行優化,根據采場寬度范圍,設計的數值模擬方案見表2。

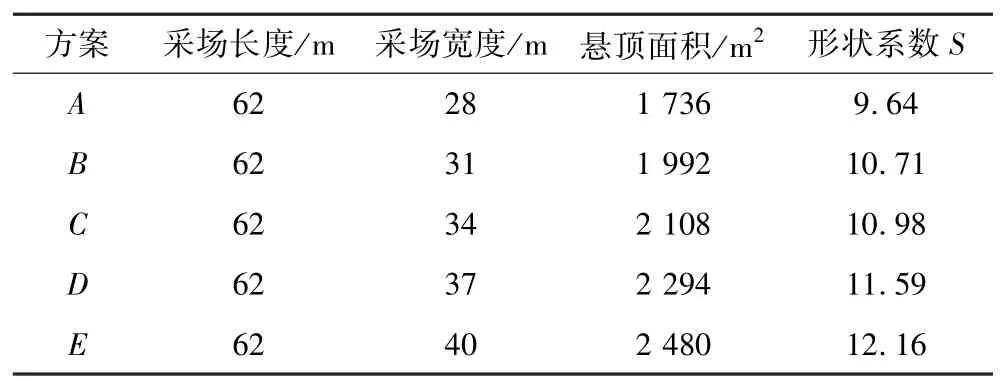
表2 數值模擬方案Table 2 Numerical simulation schemes

3.2 FLAC3D 數值模型構建

FLAC3D軟件是美國ITASCA 公司開發的三維有限差分程序,能夠進行土質、巖石和其他材料的受力分析和塑性流動分析。 該款軟件采用顯式拉格朗日算法和混合—離散分區技術,在塑性破壞和塑性流動方面有著顯著優勢[19-20]。 同時由于其無須整合剛度矩陣,在解算三維問題時所需內存較小。 故本研究采用該款軟件進行數值模擬分析。

根據采場尺寸,模擬所用到的網格模型通常為3～5 倍的研究范圍,因此構建的網格模型尺寸為600 m×600 m×500 m(長×寬×高),如圖3 所示。 模型邊界條件為:底部約束垂直位移,前后左右4 個邊界采用固定界面法向位移,由于模型尺寸延伸至地表,因此不再對頂部施加載荷,采用自然邊界。 巖體采用Mohr-Coulomb 模型,模型參數取值見表3。

表3 數值模擬力學參數Table 3 Mechanical parameters of numerical simulation

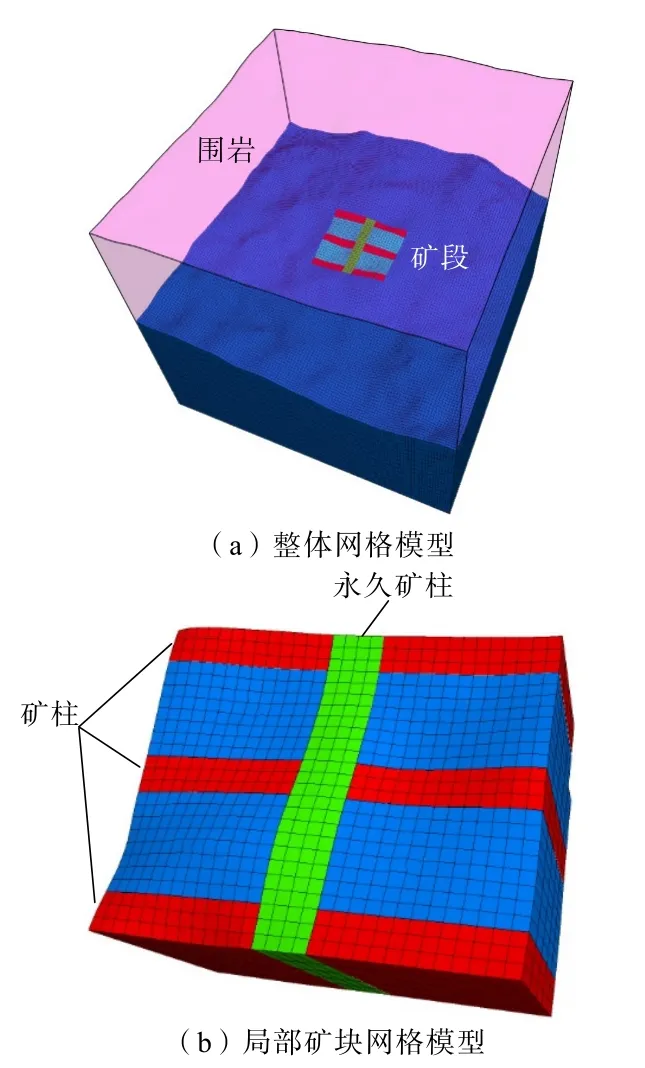
圖3 數值模擬網格模型Fig.3 Grid model for numerical simulation

3.3 計算結果分析

3.3.1 應力分析

由于礦房中間位置為最容易發生崩落的位置,故本研究取中間位置的應力云圖進行分析,結果如圖4所示。 對礦柱上的垂直應力分別進行了統計,結果如圖5 所示。 由圖4、圖5 可知:隨著采場寬度增加,礦柱上垂直方向的應力增大;最大值出現在方案E中,礦柱中垂直應力為27.4 MPa,顯然最大垂直應力小于礦柱巖石的抗壓強度(31 MPa)。

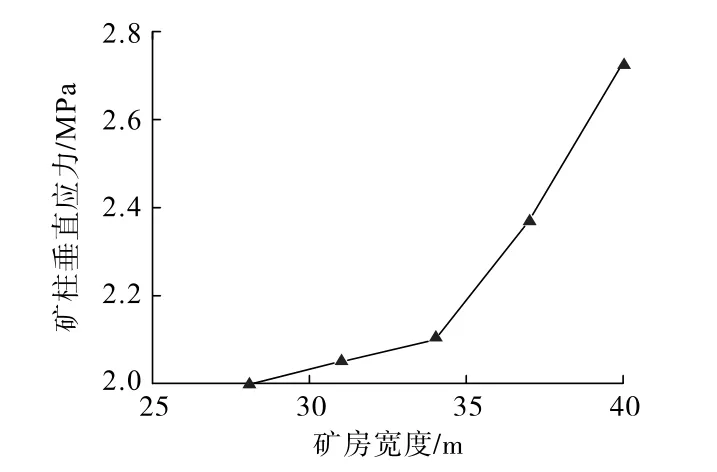
圖5 不同礦房寬度方案中的最大垂直應力Fig.5 Maximum vertical stress in different schemes

礦房上部的拉應力是預測巖體崩落的重要指標,一旦拉應力超過抗拉強度,往往將會從礦房中部位置產生巖塊的崩落,造成安全隱患。 對不同方案中的最大拉應力進行了統計,結果如圖6 所示。 由圖6 可知:隨著礦房寬度增加,拉應力逐漸增大,5 個方案對應的拉應力分別為0. 23、0. 28、0. 32、0. 53、0. 62 MPa,最大拉應力為0.62 MPa(方案E),顯然5 個方案中的最大拉應力小于礦石的抗拉強度。

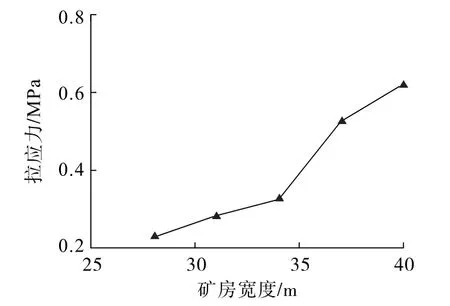
圖6 不同礦房寬度方案中的最大拉應力Fig.6 Maximum tensile stress in different schemes

綜合最大垂直應力和最大拉應力可以看出,盡管5 個方案的應力值均小于巖石強度,但對于方案D、E中的應力值接近巖石強度。 同時在方案A至方案C中垂直應力與拉應力增長相對緩慢,從方案C到方案D垂直應力與拉應力增長幅度較大。

3.3.2 位移分析

礦房中的礦體一旦開采后,礦房上方的頂板將失去原始支撐,出現頂底板向開采空間擠壓、頂底相互移近現象。 因此,頂底板的移近量是采場空間安全性的重要指標。 5 個方案的位移云圖如圖7 所示。 分析可知:隨著礦房寬度增加,頂底板移近量逐漸增大。移近量最大值發生在礦房中部位置,對5 個方案開采后的頂底板移近量進行了統計,結果如圖8 所示。 由圖8 可知:隨著礦房寬度增大,最大移近量分別為11.83、13.43、14.9、17.53、19.25 cm。 除了方案C、D存在微小波動外,頂底板移近量與礦房寬度近似呈線性關系。

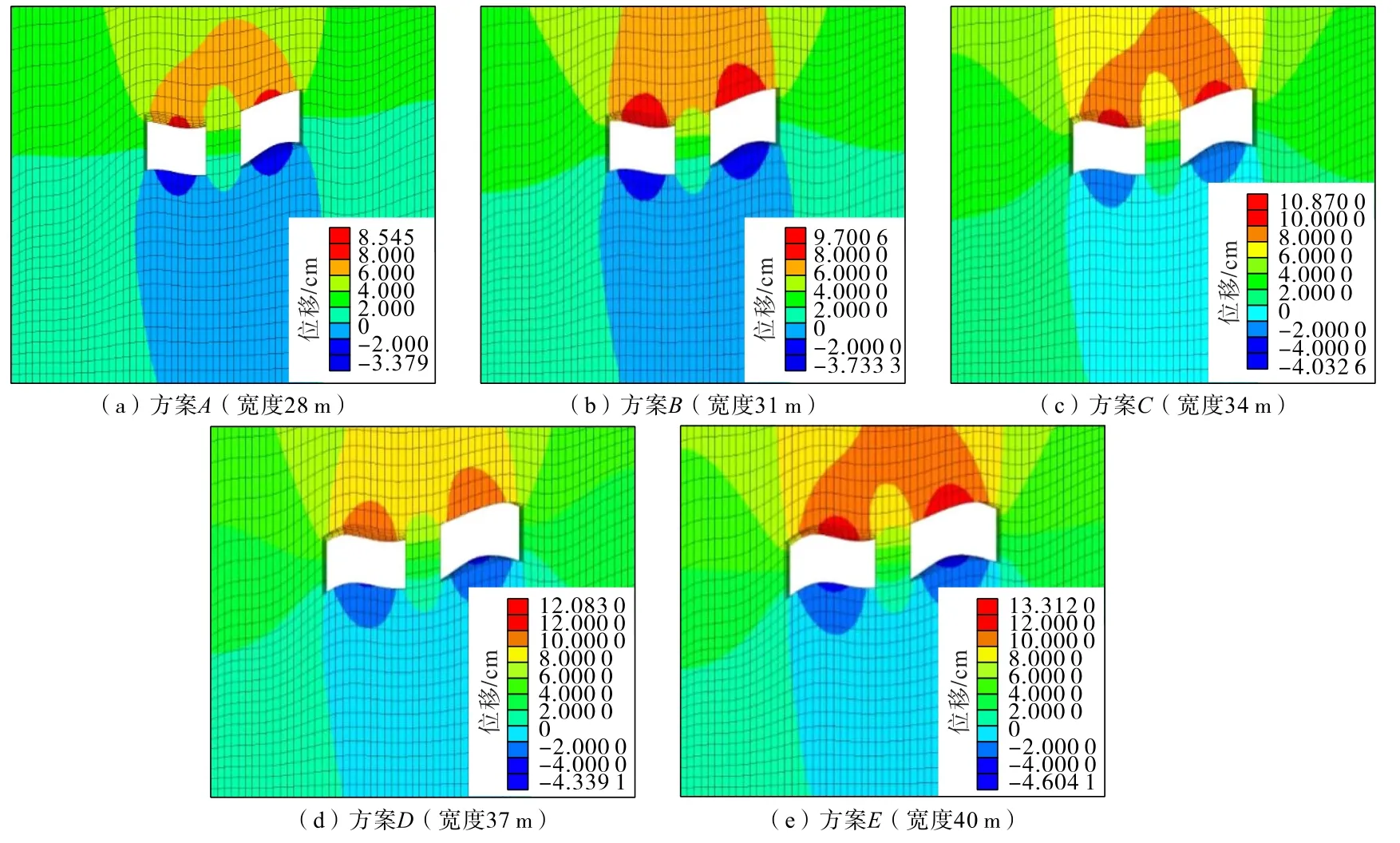
圖7 不同礦房寬度方案中頂底位移云圖Fig.7 Nephogram of roof and floor displacement in different room widths schemes

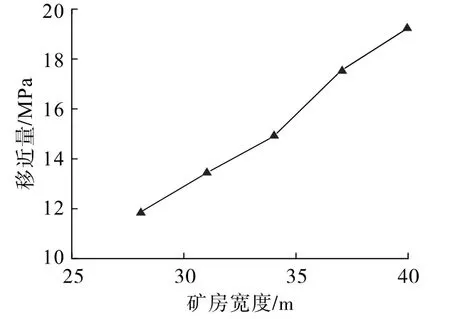
圖8 不同礦房寬度方案中頂底板移近量Fig.8 Displacement of roof and floor under different room width schemes

由上述分析可知:5 個方案的圍巖基本能夠保持穩定,都具備了一定的自支撐能力。 方案中D、E的應力值趨近于巖石強度,故不建議采納兩者。 綜合考慮經濟效益與安全性,認為方案C(寬度為34 m)為最佳方案。 該方案充分利用了圍巖自身承載能力,同時在一定支護的前提下,圍巖穩定性相對可控。

4 結 論

(1)基于山東半島某礦現場地質條件,利用Mathew 穩定圖表法,計算得到在相對穩定情況下的采場結構參數,在綜合考慮利用圍巖自身支撐能力的基礎上,給出了采場寬度合理取值范圍為28. 36～42.17 m。

(2)利用FLAC3D軟件對采場進行了數值模擬分析,不同寬度方案下應力場與位移場的數值模擬結果表明,34 m 采場寬度為最優參數。