改進Copula函數(shù)在中型水庫枯期徑流預測中的應用

白天竺

(遼寧省鐵嶺水文局，遼寧 鐵嶺 112000)

對于中型水庫而言，其主要用于區(qū)域灌溉供水和發(fā)電，尤其是在枯水期，需要對其徑流進行預測，從而制定相應的供水和發(fā)電計劃[1]。因此對于中型水庫而言，其枯水期徑流預測精度的高低，直接影響水庫的調(diào)度效益[2]。當前，對于水庫枯水期徑流預測取得一定研究成果[3-8]，其中Copula函數(shù)通過建立水庫枯水期徑流數(shù)據(jù)系列，對其未來變化概率進行趨勢預測，預測效果要好于傳統(tǒng)趨勢預測模型，但傳統(tǒng)Copula函數(shù)需要對不同數(shù)據(jù)系列進行概率密度的推求，使得其求解精度往往不高[9]。有學者針對傳統(tǒng)Copula函數(shù)求解精度不高的局限，引入變量條件概率邊際分布函數(shù)對其進行改進，并在國內(nèi)一些大型水庫枯水期徑流預測中得到相關(guān)應用[10-15]，應用結(jié)果均好于傳統(tǒng)Copula函數(shù)。但改進的Copula函數(shù)在中型水庫枯水期徑流預測中還未得到相關(guān)應用，大型水庫多為季節(jié)調(diào)節(jié)型，其枯水期徑流預測精度相比較高，而對于中型水庫而言，其枯水期徑流受季節(jié)調(diào)蓄作用影響較大，因此其徑流預測難度較高，為提高中型水庫枯水期徑流預測的精度，引入改進的Copula函數(shù)對鐵嶺地區(qū)中型水庫進行枯水期徑流預測，研究成果對于中型水庫枯水期徑流預測方法具有重要參考價值。

1 改進的Copula函數(shù)

對于任何一個變量X和Y按照Copula函數(shù)原理建立聯(lián)合概率法密度分布函數(shù)C(u，v)，其條件概率密度函數(shù)H(X，Y)的計算方程為：

H(X，Y)=C(u，v)

(1)

其中：

u=Fx(x)=P(X≤x)

(2)

v=FY(y)=P(Y≤y)

(3)

式中，u和v—變量條件概率密度函數(shù)；FX和FY—各變量對應的概率函數(shù)。

改進的Copula函數(shù)對水庫枯水期徑流采用二元模型進行概率密度分布函數(shù)的構(gòu)建，并計算其聯(lián)合概率分布函數(shù)的特征值：

(4)

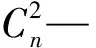
對構(gòu)建的Copula函數(shù)采用K-S檢驗方法進行離差檢驗：

(5)

式中，Cemp、Ci—概率密度函數(shù)的邊際密度計算系數(shù)。

相鄰月份徑流概率條件分布采用改進Copula函數(shù)進行描述，任一個系列的月枯期徑流量采用前一月份已知的水庫枯期徑流進行推求，其計算步驟為：

(1)計算枯期徑流序列邊緣概率函數(shù)：

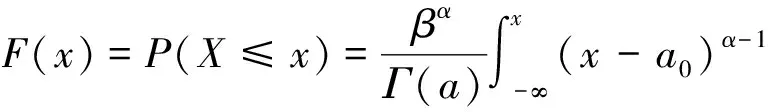
(6)

式中，α、β、α0—概率密度函數(shù)分布參數(shù)；x—徑流預測值，m3；Γ(α)—條件概率密度分布函數(shù)。

(2)計算相鄰月份枯期徑流條件概率分布函數(shù)：

(7)

式中，ut，n+1—推求的相鄰時間段的水庫枯期徑流量預測值，m3；St，St-1—不同時間段枯水期徑流變量概率密度函數(shù)；xt，n+1—水庫枯水期總的徑流量預測值，m3；Ft—預測變量在時間t內(nèi)的概率分布函數(shù)。

水庫枯水期徑流預測變量按照P-Ⅲ型分布進行計算：

(8)

式中，Φt—模型概率密度函數(shù)的偏態(tài)系數(shù)；xt，n+1，xt—不同時間段的徑流預測樣本數(shù)據(jù)系列。

改進的Copula函數(shù)對水庫枯水期徑流預測序列進行置信度區(qū)間的設置：

(9)

(10)

式中，uup和ulow—樣本序列置信區(qū)間最高和最低值；xup和xlow—預測變量置信區(qū)間的最高和最低值。

2 模型應用

2.1 分析數(shù)據(jù)

以鐵嶺地區(qū)寇河誠信中型水庫為具體實例，水庫主要功能為灌溉供水，水庫枯水期水量調(diào)度的關(guān)鍵在于其枯水期徑流預測精度的高低。11月份～次年的4月份為誠信水庫枯水期月份，結(jié)合水庫2000—2020年近20年的枯水期徑流數(shù)據(jù)系列作為分析數(shù)據(jù)，其中枯水期徑流預測變量的概率密度分布函數(shù)采用2000—2015年徑流數(shù)據(jù)序列進行計算，2011—2020年的枯水期徑流系列主要用于對比分析改進前后的Copula函數(shù)在誠信水庫枯水期徑流預測的精度。

2.2 模型構(gòu)建

采用誠信水庫2000—2015年枯水期徑流數(shù)據(jù)作為改進前后Copula函數(shù)變量計算序列樣本，分別對不同時間尺度下模型的參數(shù)進行設定，結(jié)果見表1。

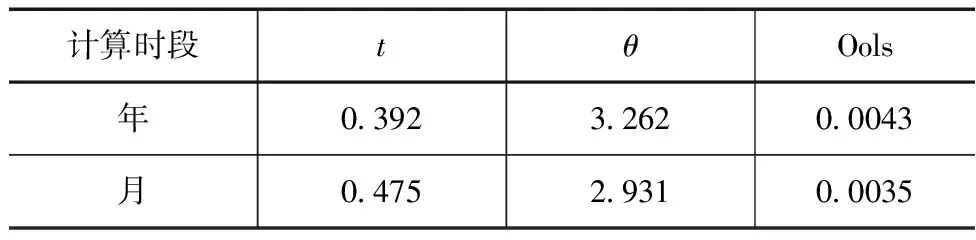
表1 改進前后Copula函數(shù)計算變量參數(shù)

2.3 年尺度預測精度對比

結(jié)合誠信水庫在2011—2020年11月份～次年的4月份實際入庫水量，對比分析改進前后的Copula函數(shù)在水庫枯水期年尺度的入庫水量的預測精度，并對改進前后模型預測值和實際入庫量之間的相關(guān)系數(shù)和誤差分布進行統(tǒng)計，統(tǒng)計分析結(jié)果見表2，如圖1所示。

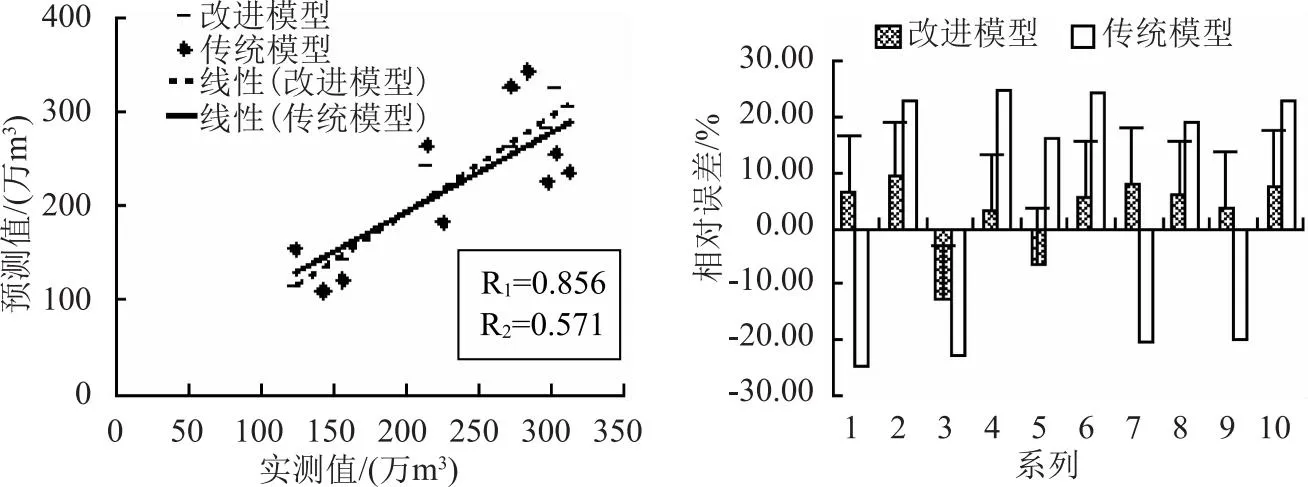
圖1 誠信水庫年尺度枯水期預測值和實際值誤差統(tǒng)計

從改進前后Copula函數(shù)下誠信水庫年尺度入庫水量預測精度對比結(jié)果可看出，相比于改進前的Copula函數(shù)，改進后的Copula函數(shù)其枯水期徑流預測精度得到明顯改善，改進后誠信水庫在枯水期年尺度下的入庫水量預測值和實際入庫水量之間的相對誤差均在±10%以內(nèi)，而改進前的相對誤差均高于±10%，相比于改進前，改進后水庫枯水期徑流預測相對誤差均值降低13.4%。從絕對誤差對比可看出，改進前，各年份誠信水庫枯水期徑流預測值和實際入庫量之間的絕對誤差在27.72萬m3～69.84萬m3之間，且具有明顯的年際變幅，而改進后誠信水庫枯水期徑流預測的絕對誤差可控制在30萬m3之內(nèi)，且年際變幅較小。從改進前后Copula函數(shù)下誠信水庫枯水期年尺度預測誤差統(tǒng)計結(jié)果可看出，相比于改進前，改進后的相關(guān)系數(shù)達到0.856，相關(guān)系數(shù)提高0.285，相對誤差分布也更為集中。

2.4 月尺度預測精度對比

對于水庫而言，枯水期徑流在月尺度變化更為明顯，因此在年尺度精度對比分析基礎(chǔ)上，分別結(jié)合改進的Copula函數(shù)對枯水期各月徑流量進行預測精度對比，并統(tǒng)計改進前后徑流預測的誤差分布，統(tǒng)計結(jié)果分別見表3，如圖2所示。

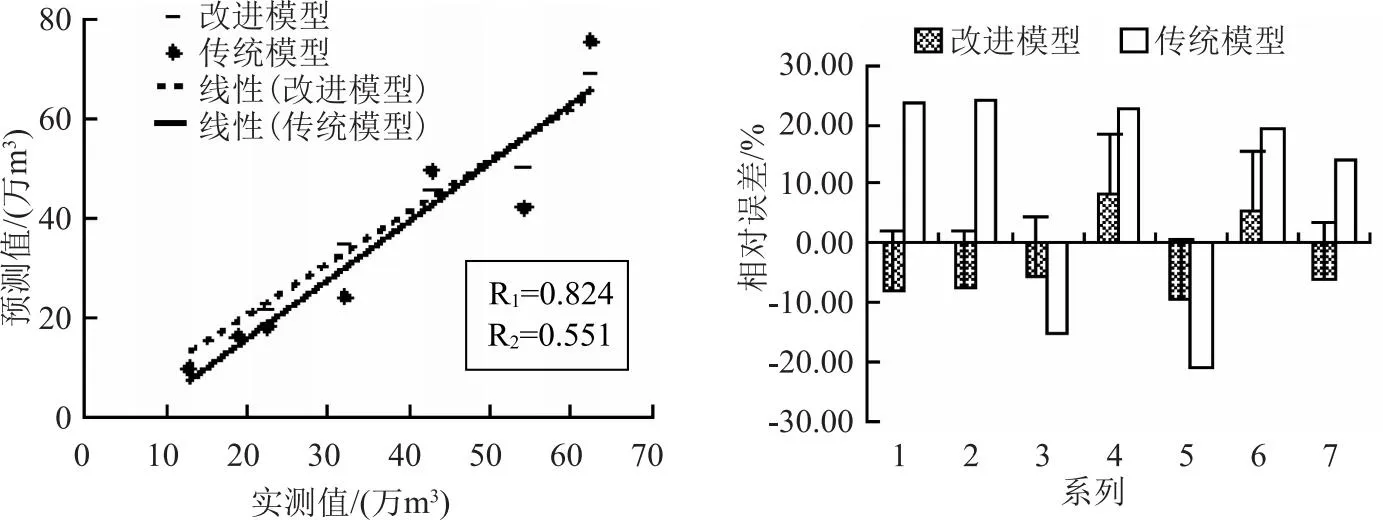
圖2 誠信水庫月尺度枯水期預測值和實際值誤差統(tǒng)計

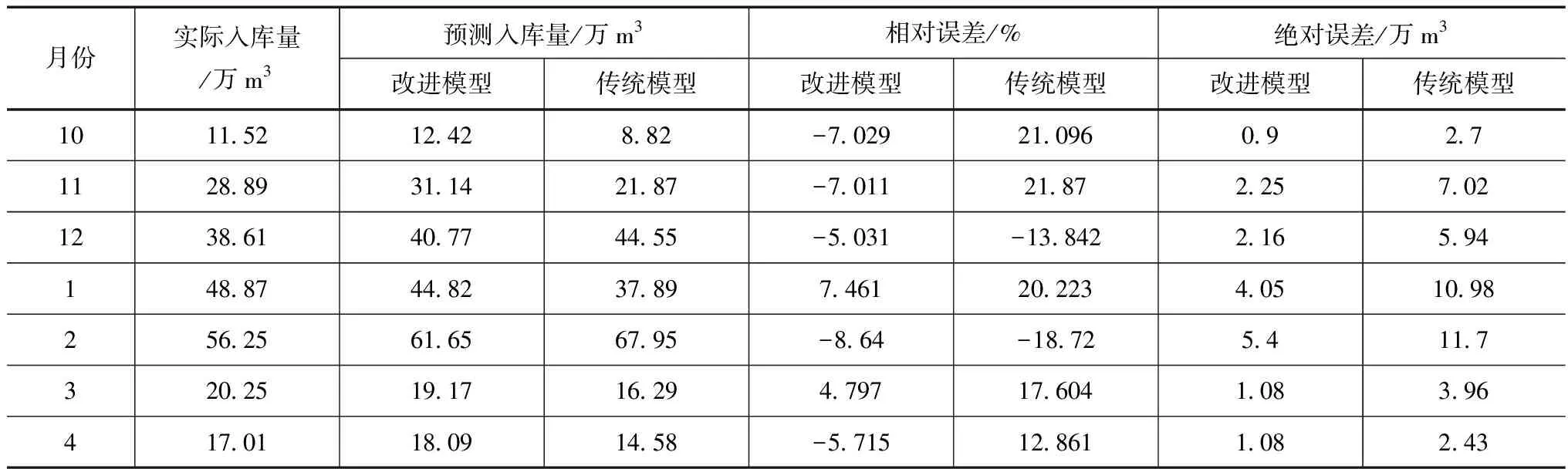
表3 改進前后Copula函數(shù)下誠信水庫月尺度入庫水量預測精度對比

從改進前后Copula函數(shù)下誠信水庫月尺度入庫水量預測精度對比可看出，相比于改進前，改進后的Copula函數(shù)下誠信水庫月尺度入庫水量預測精度也同樣明顯改善，改進后誠信水庫枯水期各月入庫水量預測值和實際入庫水量之間的相對誤差均在±10%以內(nèi)，且要低于年尺度預測相對誤差，這主要是因為年尺度下徑流預測有均化現(xiàn)象，一定程度提高了其預測誤差。相比于改進前，在月尺度上改進后的Copula函數(shù)下誠信水庫月尺度入庫水量預測值和實際入庫水量之間的相對誤差均值降低11.5%，絕對誤差降低3.97萬m3。從誠信水庫月尺度枯水期預測值和實際值誤差統(tǒng)計結(jié)果可看出，對于月尺度而言，改進后的Copula函數(shù)其徑流預測值和實際入庫水量之間的相關(guān)系數(shù)提高0.273，誤差分布也相比于改進前更為集中。

3 結(jié)語

(1)在采用改進后Copula函數(shù)對中型水庫進行枯水期徑流預測時，應結(jié)合K-S檢驗對其預測變量序列的概率密度分布函數(shù)進行離差檢驗，檢驗系數(shù)低于0.95時其變量概率密度函數(shù)可通過檢驗。

(2)在進行中型水庫枯水期逐月徑流預測時，可降低其預測變量置信區(qū)間的上限值，通常可在0.5～1.5之間進行調(diào)整，可解決其不同月份之間徑流預測差異較大的問題。

(3)降水量變化對于中型水庫枯水期徑流預測影響較大，在后續(xù)研究中可建立降水和徑流量的雙變量Copula函數(shù)，充分考慮降水變化對其枯水期徑流影響。