GNSS網基線檢核對平差結果的影響

邢金玉 金 鵬 房大為 許永強

（1.河北省第一測繪院，河北 石家莊 050031；2.北京市測繪設計研究院，北京 100038；3.城市空間信息工程北京市重點實驗室，北京 100038）

0 引言

在施測全球導航衛星系統（global navigation satellite system，GNSS）控制網時，通常是使用數量不等的GNSS 接收機在外業進行數據采集，采用隨機軟件下載觀測數據并進行基線向量的解算，解算完畢后使用隨機軟件進行平差計算，或者從隨機軟件中導出基線解文件，使用經過國家認定的商用平差軟件對GNSS 網進行平差計算，得到我們所需要的控制網的成果。

GNSS 控制網的誤差來源主要包括三類：與衛星相關的誤差、與大氣傳輸相關的誤差、與接收機相關的誤差，在實際的作業過程中通常需要解決的是與接收機相關的誤差，包括接收機安置誤差以及觀測誤差［1］。

為確保GNSS 控制網測量成果的精度和可靠性，在相應的測量規范中，對于不同等級控制網的施測，其觀測時段數、時段長度均有具體的規定，根據《全球定位系統（GPS）測量規范》（GB/T 18314—2009）10.1.2 的技術規定，C 級網的觀測時段數≥2，時段長度≥4［2］。

GNSS 控制網的基本元素是GNSS 基線向量，因而基線向量質量的好壞對GNSS 控制網的質量有著直接的影響，在數據處理中，應該采用相應的質量控制措施，以確保其質量能滿足規范和項目的要求，GNSS 基線的質量依賴于GNSS 觀測數據的質量和基線處理方法。

基線向量解算完成后，評定基線解算結果質量的指標有兩類，一類是基于測量規范的控制指標，另一類是基于統計學原理的參考指標。在工程應用中，規范的控制指標必須滿足，而參考指標則不作為判別質量是否合格的依據［3］。

在平差過程中，雖然采用GNSS 同步觀測的基線向量解作為觀測量能消除各同步網位置基準的系統誤差對平差結果的影響，但是采用坐標解作為平差的觀測量進行平差得到的結果更能真實地反映控制網的實際精度水平［4］。

在除了剔除含有粗差的基線向量外，還需要對基線處理結果的質量進行檢核，檢核內容包括同步環閉合差、異步環閉合差以及重復基線邊長較差的檢核。

如果不進行這些檢核就進行平差計算會對平差結果有多大的影響，下面就作業實例進行探討。

1 作業實例

該C 級GNSS 網位于河北省南部，共聯測控制點13 個，其中包含省級連續運行參考站（continuously operating reference stations，CORS）2 個（HDWX、XTLX），國家B 級控制點2 個（1179、1120），新建C 級控制點9 個，使用5 臺Trimble R8進行外業數據采集，平均上站率≥2，采用隨機軟件TBC3.60 進行數據下載、基線解算與基線檢核，使用武漢大學測繪學院研制開發的科傻數據處理系統（CosaGPS 5.21）進行控制網的平差計算，CORS 基準站的起算坐標數據為自然資源部西安大地測量數據處理中心2011 年平差出來的最新成果。控制網觀測網如圖1所示。

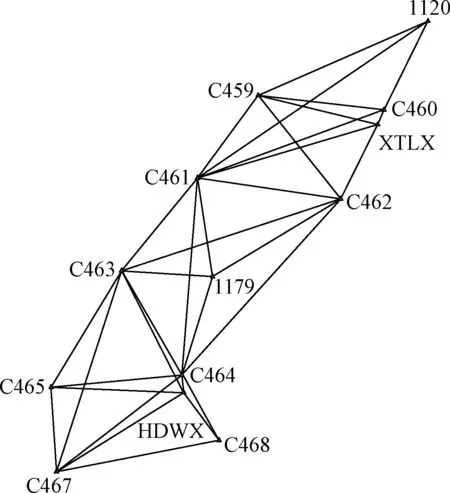
圖1 測量標志重建C級GNSS觀測網

基線解算采用隨機軟件TBC3.60，解類型設置為固定，頻率使用多頻，水平精度標志設置為0.050 m+1.0×10-6D，D為相鄰點間距離（km），垂直精度標志設置為0.100 m+1.0×10-6D。

在數據統計分析中，將所有值平方求和，求其均值后再開平方，就得到均方根（root mean square，RMS）的數值，常用RMS值來分析噪聲。

RMS 是觀測值中噪聲的量度，通常認為RMS值越小越好。要達到“通過”狀態，RMS 值必須小于“標記”值，雖然RMS檢驗包含單頻標記和失敗域以及雙頻標記和失敗域，但本次作業選擇的是雙頻標記和失敗域作為檢驗項，標記值設置為：0.005 m+0.5×10-6D［5］。

相對定位是指在觀測值間求差并利用求差后的差分觀測值進行定位，在相對定位中常用雙差觀測值求解基線向量，由雙差觀測值列出誤差方程式，然后利用最小二乘平差原理求解基線向量，基線向量的解算是一個復雜的計算過程，實際處理時要顧及時段信號間斷引起的數據剔除、劣質觀測數據的發現及剔除、衛星變化引起的整周未知參數的增加等問題。

基線解算完成后進行了基線檢核，基線檢核設置環的邊數為3 條，固定誤差設置為5 mm，比例誤差系數設置為1×10-6D，判定合格與不合格的標準為環閉合差Ws以及坐標分量閉合差WX、WY、WZ均不能超限，基線檢核結果統計如表1所示。

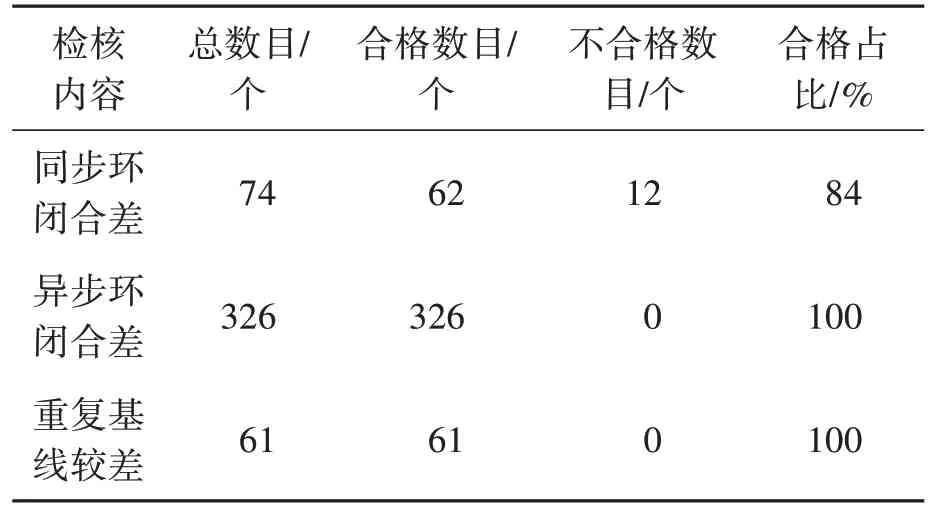
表1 基線檢核統計表

通過表1 看出，只有同步環閉合差有不合格的情況出現，這也與同步環閉合差限差要求嚴格相對應，表2 是對不合格的同步環超限情況的統計。

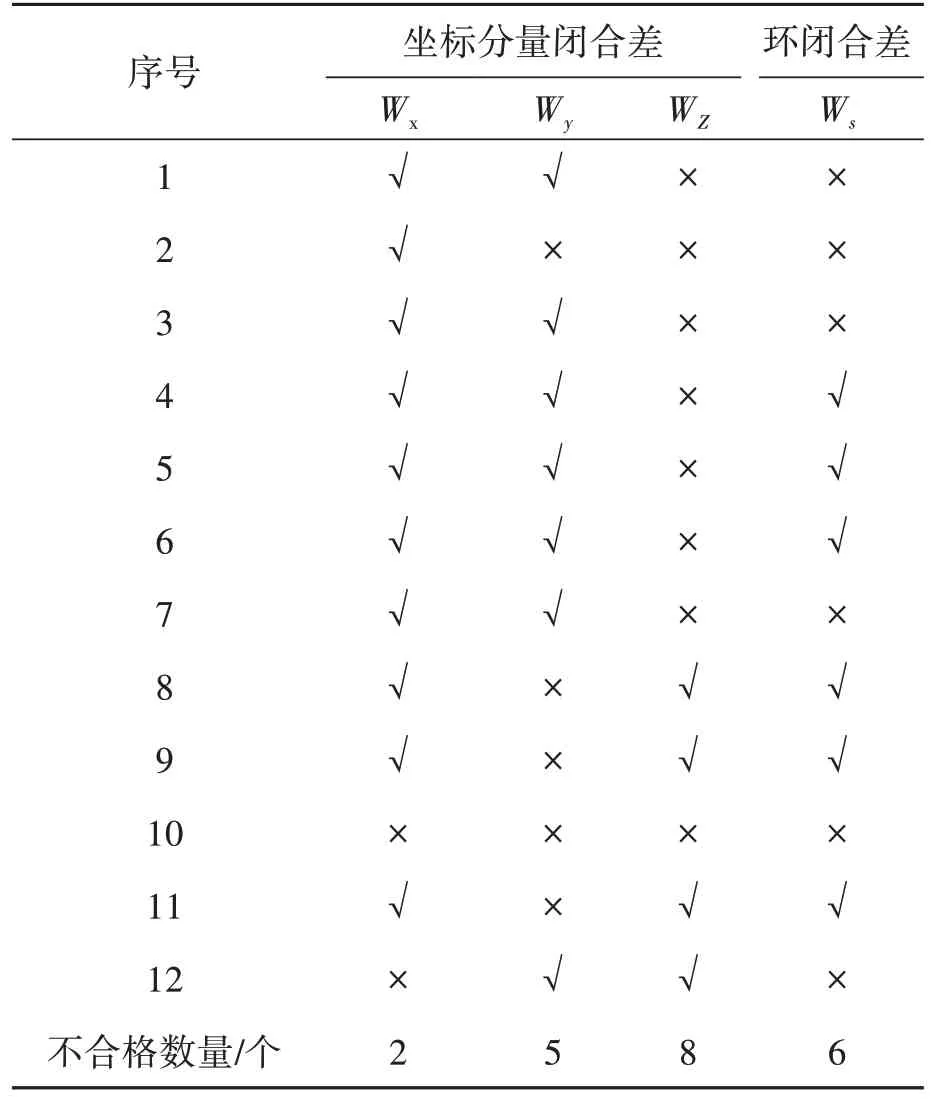
表2 同步環超限情況統計表

從表2 中看出，坐標分量閉合差WZ不合格的最多，為8 個，6 個不合格的環閉合差WS中有1 個是由Wx直接 引起（序號12），1 個是由Wy和WZ引起（序號2），3 個是由WZ直接引起（序號1、3、7），剩余1個是由Wx、Wy、WZ三者共同作用引起的（序號10），另外有3 個WZ雖然不合格（序號4、5、6），但并未造成Ws的不合格。

鑒于WZ不合格數量最多，因此在外業作業中精準設置儀器以及準確量取天線高度很有必要。

接收機天線相位中心相對測站標石中心位置的誤差叫接收機位置誤差。這里包括天線的置平、對中不精準引起的誤差和量取天線高誤差。如當天線高度為1.6 m 時，置平誤差為0.1°時，可能會產生對中誤差3 mm，因此，在精密定位時，必須仔細操作，以盡量減少這種誤差的影響。在變形測量中，應采用有強制對中裝置的觀測墩［6］。

除了上面提到的接收機位置誤差或者叫安置誤差外，另外一種與接收機誤差叫觀測誤差，為提高精度，應使位置精度因子（position dilution of precision，PDOP）值盡可能小，這就是說，應選擇由用戶位置和衛星位置構成的四面體的體積為最大的一組衛星進行觀測［7］。

1.1 使用所有基線向量平差計算

用多臺接收機進行多次觀測，就形成一個由GNSS 基線向量組成的GNSS 網，網中包含地面起算數據和觀測數據，這就產生了GNSS 網與地面數據的三維聯合平差，地面觀測值可按公式列出它們的誤差方程，建立了全部基線向量的誤差方程后與地面觀測值的誤差方程聯合組成法方程，就可以解出各點的大地坐標和轉換參數的平差值［8］。

基線向量解算完成后，不進行基線檢核，即不考慮同步環閉合差不合格的情況下導出基線向量文件，使用全部基線向量進行GNSS網平差。

首先固定一個CORS 站的三維坐標進行三維無約束平差，GNSS 網中含有許多閉合條件，通過三維無約束平差可消除閉合條件的不符值，并建立網的基準，即網的位置、方向和尺度基準。基線向量本身已經確定了方向和尺度基準，與網的平差方法無關，而網的位置基準則與平差的方法密切相關。

三維無約束平差的目的是考察網本身的內符合精度以及考察基線向量之間有無明顯的系統誤差和粗差，同時為GNSS 大地高與公共點正常高聯合確定GNSS 網點的高程異常，提供平差處理后的大地高程數據［9］。

在三維無約束平差結果中，三維基線向量的殘差均合格，其中最弱邊為HDWX-C464，其邊長相對中誤差為1/3 090 000。

三維約束平差基本方法為建立包含地心系到參心系的轉換參數和參心系下坐標參數在內的統一函數模型，平差后可直接得出待定點在參心系下的坐標。

固定兩個CORS 站的坐標進行三維約束平差，兩個B 級點作為校核點，在平差結果中，三維基線向量殘差均合格，其中最弱邊為HDWXC464，其邊長相對中誤差為1/2 986 000，最弱點為C460，其點位中誤差為Mp=1.84 cm，其坐標分量中誤差分別為Mx=0.69 cm，My=1.31 cm，Mz=1.09 cm。

1.2 使用檢核后的基線向量平差計算

由于有12個三邊同步環是不合格的，所以只對組成不合格同步環的基線向量進行重新計算或刪除，經過反復計算，最后得到的基線檢核結果如表3所示。

基線是相關的，基線間的相關性對解算結果是有影響的，基線間的這種相關性容易造成粗差的轉移和隱藏，所以對于高精度GNSS 網的數據處理，必須考慮基線間的相關性，不合格的基線應該在平差前剔除出去［10］。

由表3看出，正是由于刪除了部分基線向量，造成了合格的同步環、異步環以及重復基線的數目都有不同程度的減少，其中異步環減少的最多，導出基線向量文件進行平差計算，固定的點和平差過程與首次的計算完全相同。

三維無約束平差結果中，三維基線向量殘差均合格，其中最弱邊為HDWX-C466，其邊長相對中誤差為1/6 469 000；在三維約束平差結果中，三維基線向量殘差均合格，其中最弱邊為HDWX-C466，其邊長相對中誤差為1/6 236 000，最弱點為C460，其點位中誤差為MP=2.03 cm，其坐標分量中誤差分別為Mx=0.76 cm，My=1.45 cm，Mz=1.20 cm。

2 比較與分析

根據上面的平差計算成果，可以通過對比發現兩次平差結果的差異，并對產生差異的原因進行分析。

2.1 平差結果比較

由于兩次平差所采用的基線向量不同，造成最弱邊不是同名基線，對最弱邊的比較已經沒有意義，所以我們只對點位精度進行比較，首先比較兩次平差后坐標成果的差值，差值為首次平差結果減去第二次平差結果，見表4。

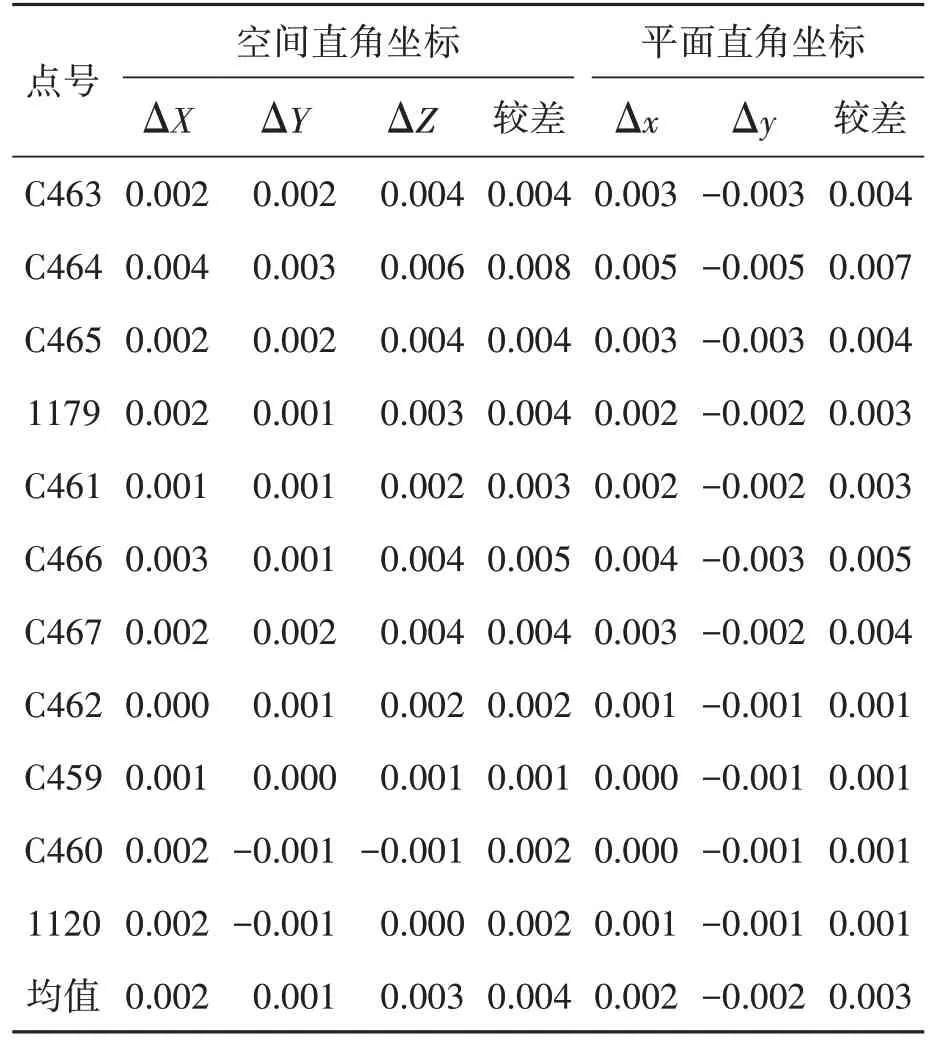
表4 兩次平差成果坐標較差表 單位：m

由表4可以看出，在空間直角坐標系中，C464坐標較差最大，為0.008 m，C459 坐標較差最小，為0.001 m，均值為0.004 m。在平面直角坐標中，較差最大與最小的點也是該兩個點，同時C462、C460、1120是較差最小的點。

以空間直角坐標的點位精度來比較兩次平差結果精度的不同，未進行基線檢核，選取所有基線向量的基線解文件進行平差計算，點位精度如表5所示。

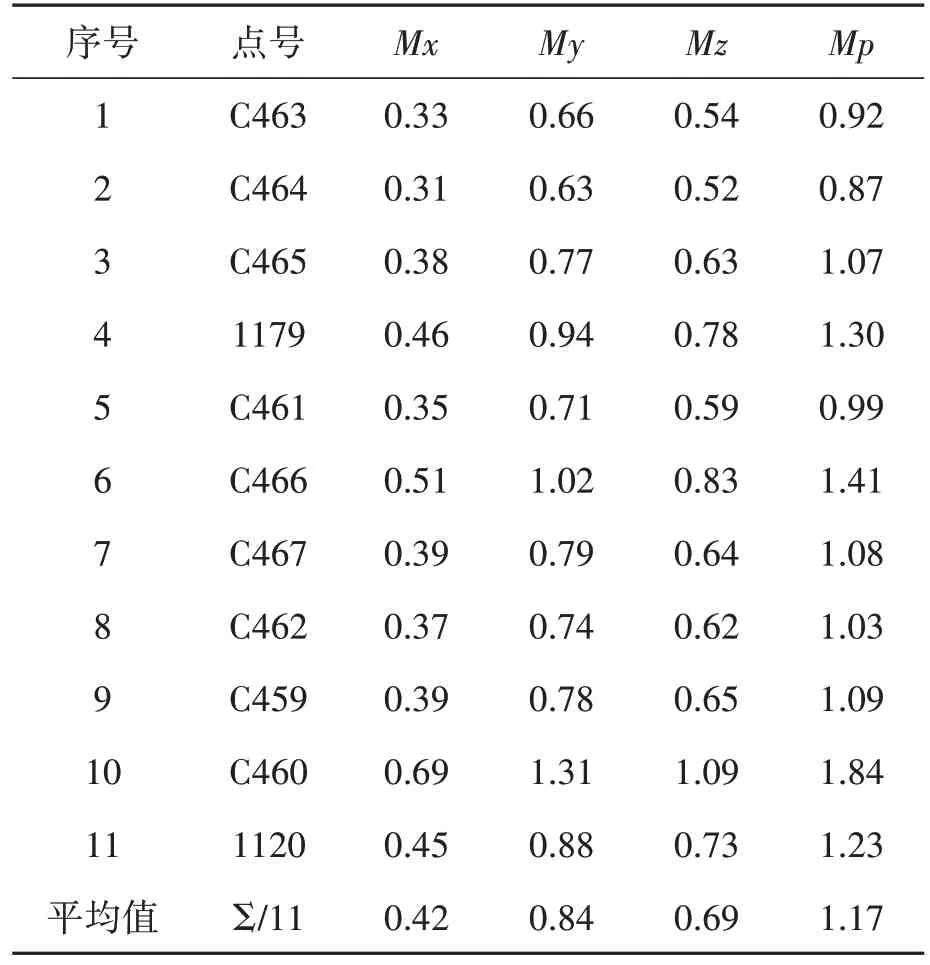
表5 首次平差點位精度表 單位：cm

進行基線檢核后提取基線解文件進行平差計算，平差的設置與第一次一樣，平差報告中精度評定中點位精度情況見表6。

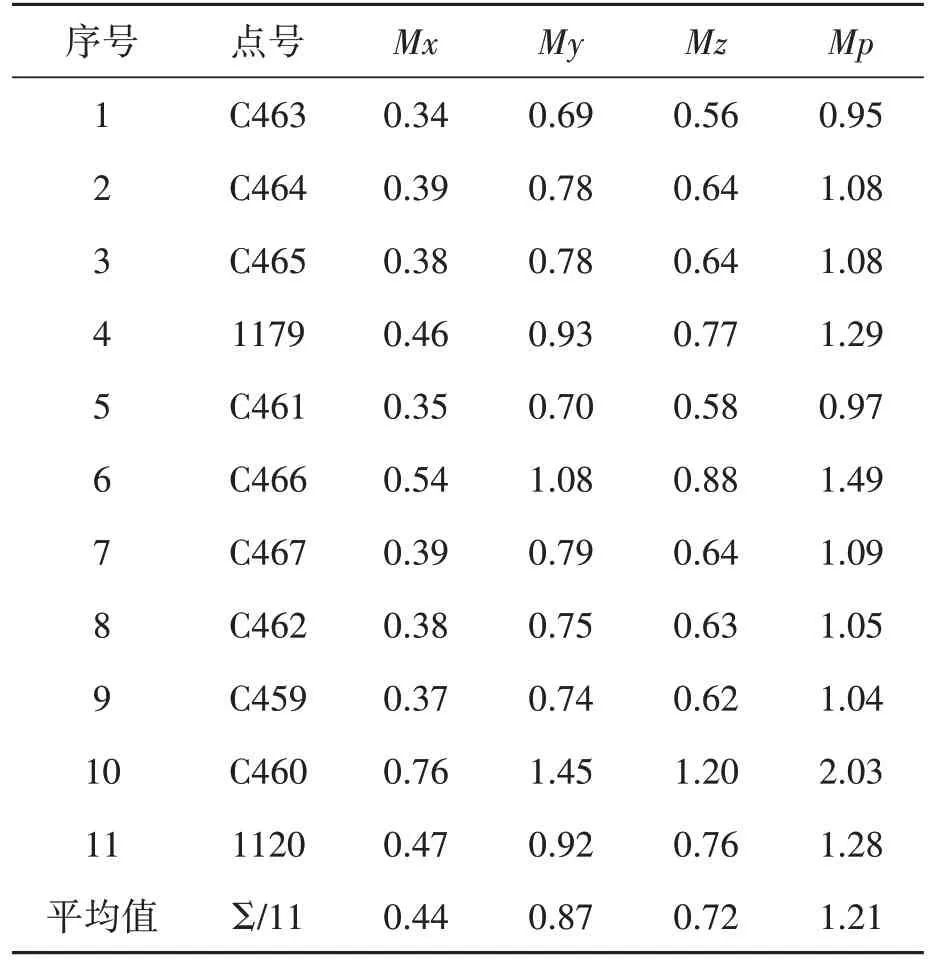
表6 二次平差點位精度表 單位：cm

通過對表5、表6 兩個表格的對比，發現進行基線檢核后的平差結果中除了1179、C461、C459三個點的精度略有提高外，其他8 個點的點位精度反而都降低了，什么原因造成了這種結果，是本研究需要探討的問題。

2.2 原因分析

既然使用全部基線向量進行平差的結果點位精度更高一些，是不是就應該選取全部基線向量進行平差計算，而不需要進行基線檢核了呢。

由表4 可知，兩次平差結果中的空間直角坐標較差均值為4 mm，平面直角坐標的坐標較差均值為3 mm，兩次平差的結果雖然無明顯變化，但是差距也不容忽視。

點位中誤差雖然可以用來評定待定點的點位精度，但是它卻不能代表該點在某一任意方向上的誤差大小，為了便于求定待定點點位在任意方向上誤差的大小，一般是通過求出待定點的點位誤差橢圓來實現的，這樣就可以比較精確地、形象而全面地反映待定點在各個方向上誤差的分布情況。

這說明點位中誤差在反映控制網的精度方面有一定的局限性，在《全球定位系統（GPS）測量規范》（GB/T 18314—2009）里面“級別劃分和測量精度”一節中對C 級網的精度要求為其相對精度應不低于1×10-6，并無點位中誤差精度方面的相關要求。

精度評定需要首先得到單位權中誤差，無論是條件平差還是間接平差，單位權中誤差的公式均為

式中，p為某一個觀測值的權；v為某一個觀測值的改正數；n為觀測值個數；t為未知數個數［11］。

由兩次平差結果中提供的基本信息可以驗算單位權中誤差，表7 是兩次三維約束平差結果中提供的控制網的一些基本信息。

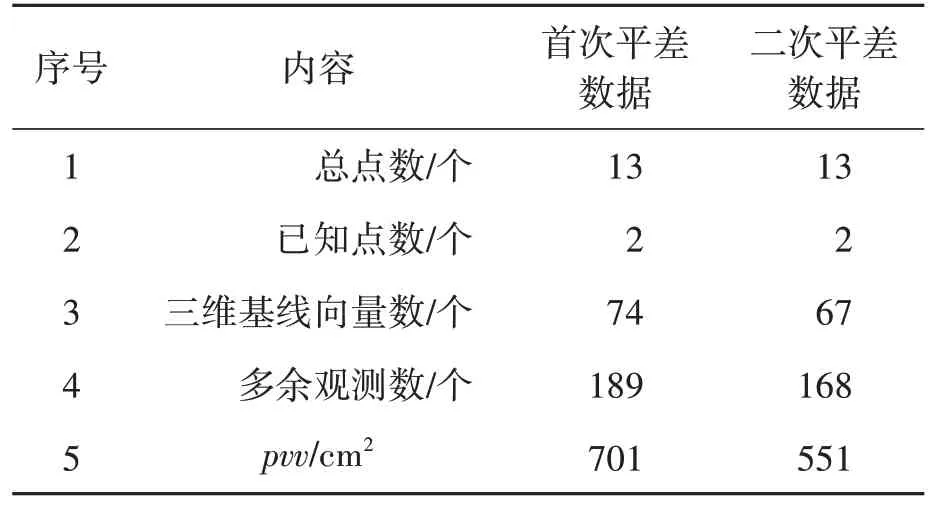
表7 控制網基本信息表

根據式（1）計算出兩次平差的單位權中誤差，對于一個確定的網來說，按最小二乘原則平差后，所得改正數v與所用平差方法無關，所以，無論GNSS 網平差取何種方法（經典平差法、偽逆平差法或擬穩平差法），其原始觀測量的單位權中誤差的計算公式是一樣的［12］。

通過計算兩次平差的單位權中誤差分別為σ1=±1.927 cm、σ2=±1.811 cm。

可以看出，第二次平差的單位權中誤差更小一些，說明第二次的平差精度要高于首次的平差，為什么第二次平差的點位精度更高一些呢，GNSS網平差后，其坐標分量中誤差可按式（2）估算。

式中，σ0為單位權中誤差；qxx、qyy、qzz、為權系數陣QXX、QYY、QZZ主對角線的相應元素，其坐標中誤差可按式（3）計算。

權系數陣與所采用的平差方法密切相關，采用不同的平差方法其計算公式也不相同，權系數陣包含了所有平差量及其函數的精度信息，所以它對于平差后網的精度評定，具有極為重要的意義［13］。

由于首次平差比第二次平差多出21 個多余觀測量，也就是增加了21 個函數相關觀測，增加了多余觀測量的點其首次平差求得的qxx、qyy、qzz比第二次平差要小，造成了未采取基線檢核就進行平差反而得到了更高的點位精度。但并不是所有的點都增加了多余觀測，這也是首次平差中仍有三個點精度低的原因，盡管如此增加的多余觀測量還是提高了多數點的點位中誤差的精度，造成了未采取基線檢核就進行平差反而得到了更高的點位精度，出現了選取所有基線向量平差會出現點位中誤差虛高的現象［14］。

點位坐標中誤差是由兩部分組成，一是單位權中誤差，二是坐標分量的協因數陣，通常情況下增加了多余觀測會造成此項變小，但增加了多余觀測并不一定能使單位權中誤差變小，因為式（1）中雖然n-t變大了，但pvv同樣也變大了，因此同一個網采用不同的基線向量進行平差時，應以單位權中誤差作為衡量網精度大小的一個重要指標，而不只是參照坐標的點位中誤差，如果得到的單位權中誤差比較小，甚至可以抵消協因數陣變大帶來的影響，使得點位中誤差也變小。

因此控制網平差前的基線檢核還是很有必要的，基線檢核會把外業觀測數據中的粗差和誤差超限部分剔除了，在國家標準和規范中對外業數據質量檢核也做了相應的規定，特別是在衛星定位城市測量技術規范里面，關于“城市GNSS 控制網建設”中對GNSS 網基線解算有著更為嚴格和詳細的規定［15］。

3 結束語

理論上GNSS 閉合環的各分量閉合差以及環閉合差是為零的，因此在各類規范中對基線檢核都有相應的規定；在基線檢核中異步環閉合差以及重復基線較差比較容易達到規范的要求，同步環閉合差容易出現不合格的情況；不合格的同步環中，坐標分量閉合差WZ不合格較多，許多環閉合差Ws不合格的原因也是由WZ不合格造成的，因此外業需要精準量取天線高；雖然選取所有的基線向量進行平差計算，有時會得到虛高的點位中誤差，但進行基線檢核還是很有必要的，也是應該必須進行檢核的。