基于不同抽樣方法的核電廠大破口失水事故BEPU 分析

王洋洋，孫曉暉，石興偉

（1.電力規劃設計總院，北京 100120；2.中國核電工程有限公司，北京 100840；3.生態環境部核與輻射安全中心，北京 100082）

最佳估算加不確定性（BEPU）分析方法同傳統的保守性分析方法相比，可獲取相對現實的分析結果和安全裕量，能在保證核電廠安全性的前提下，提高核電廠的經濟性和運行靈活性。根據國際原子能機構（IAEA）的定義[1]，最佳估算加不確定性分析方法應滿足3 個條件：對于選定的驗收準則，事故分析中不有意引入悲觀性；使用最佳估算程序；對計算結果進行不確定性分析。不確定性分析方法依據不確定性傳輸主體的不同可分為“輸入不確定性傳播”方法和“輸出不確定性傳播”方法[1]。典型的“輸入不確定性傳播”方法有美國的CSAU 和ASTRUM、德國的GRS、法國的IPSN 和西班牙的ENUSA 等。典型的“輸出不確定性傳播”方法為意大利的UMAE/CIAU。目前相比“輸出不確定性傳播”方法，“輸入不確定性傳播”方法被世界更多國家研究和使用。“輸入不確定性傳播”方法以熱工水力系統程序（最佳估算程序）為不確定性傳輸媒介，將輸入不確定性傳播到輸出不確定性，其具體流程如圖1 所示。基于特定的抽樣方法對不確定性重要輸入參數進行隨機抽樣是不確定性評估流程的重要環節，隨機抽樣參數作為熱工水力系統程序的輸入，將直接關系到目標響應參數的不確定性量化結果。

圖1 基于輸入傳遞的不確定性評估流程

美國核管會（NRC） 在1974 年發布的10CFR 50.46 輕水堆核電廠應急堆芯冷卻系統（ECCS）驗收準則[2]，成為輕水堆保守性失水事故（LOCA）分析的國際通用規范。失水事故驗收準則為：包殼峰值溫度不能超過限值（1 477 K）以防止包殼脆化；包殼總氧化率不超過氧化前包殼總厚度的17%；燃料包殼與水或蒸汽發生化學反應的產氫量不應超過堆芯所有鋯產氫量的1%；堆芯保持可冷卻的幾何形狀；保持對堆芯的長期冷卻。NRC 在1988 年對10CFR 50.46 及其附錄K 進行了修訂，LOCA 驗收準則保持不變，允許采用BEPU分析方法進行LOCA 分析，需將不確定性分析結果同驗收準則進行比較，確保驗收準則規定限制有很高的概率不被超過。盡管許多國家采用TRACE、CATHARE和RELAP5 等最佳估算程序對大破口失水事故（LBLOCA）進行了不確定性分析，但系統地基于不同抽樣方法開展響應參數不確定性量化與敏感性分析工作尚無。

本文采用RELAP5 程序建立百萬千瓦級壓水堆核電廠大破口失水事故模型，并對模型進行穩態調試和瞬態分析；采用Python3.7 基于簡單隨機抽樣（SRS）和拉丁超立方抽樣（LHS）對重要不確定性輸入參數進行隨機抽樣產生模型輸入矩陣，通過模型對輸入矩陣實施計算獲取關鍵安全參數；采用Wilks 非參數統計方法對關鍵安全參數進行不確定性量化以獲取單側統計容忍上限，采用Spearman 秩相關系數法對關鍵安全參數進行敏感性分析以識別主要影響的輸入參數。并評估2 種抽樣方法在不確定性量化和敏感性分析中的計算結果的差異。

1 模型建立

1.1 程序介紹

RELAP5/MOD3.4 程序基于非均勻、非平衡、兩流體動力學模型，采用快速半隱式數值技術求解，能夠模擬反應堆在幾乎各種運行瞬態或假想事故下的行為，廣泛應用于事故分析、規程制定、審評計算和事故緩解措施評價等各個方面。是目前國際通用的輕水堆熱工水力瞬態分析程序，可用于反應堆破口類事故分析。

1.2 模型建立

某百萬千瓦級壓水堆核電廠采用我國具有完整自主知識產權的第三代壓水堆核電技術。核電廠主系統具有3 個環路，每個環路有1 臺主泵和1 臺蒸汽發生器，系統共用1 臺穩壓器。反應堆熱功率為3 180 MW，冷卻劑平均溫度為310℃，系統正常運行壓力為15.5MPa。

采用RELAP5/MOD3.4 程序針對百萬千瓦級壓水堆核電廠的設計特點，對大破口失水事故建立最佳估算分析模型，系統節點劃分如圖2 所示。建模對象主要包括反應堆壓力容器、穩壓器、蒸汽發生器、主泵、主蒸汽系統、安注系統、主給水系統、輔給水系統、主管道和破口等。其中，壓力容器針對入口、下降環腔、下封頭、下腔室、堆芯通道、堆芯旁通通道、上腔室和上封頭等進行了模擬。安全殼采用時間相關控制體進行模擬，大破口失水事故的發生通過觸發閥打開進行模擬。

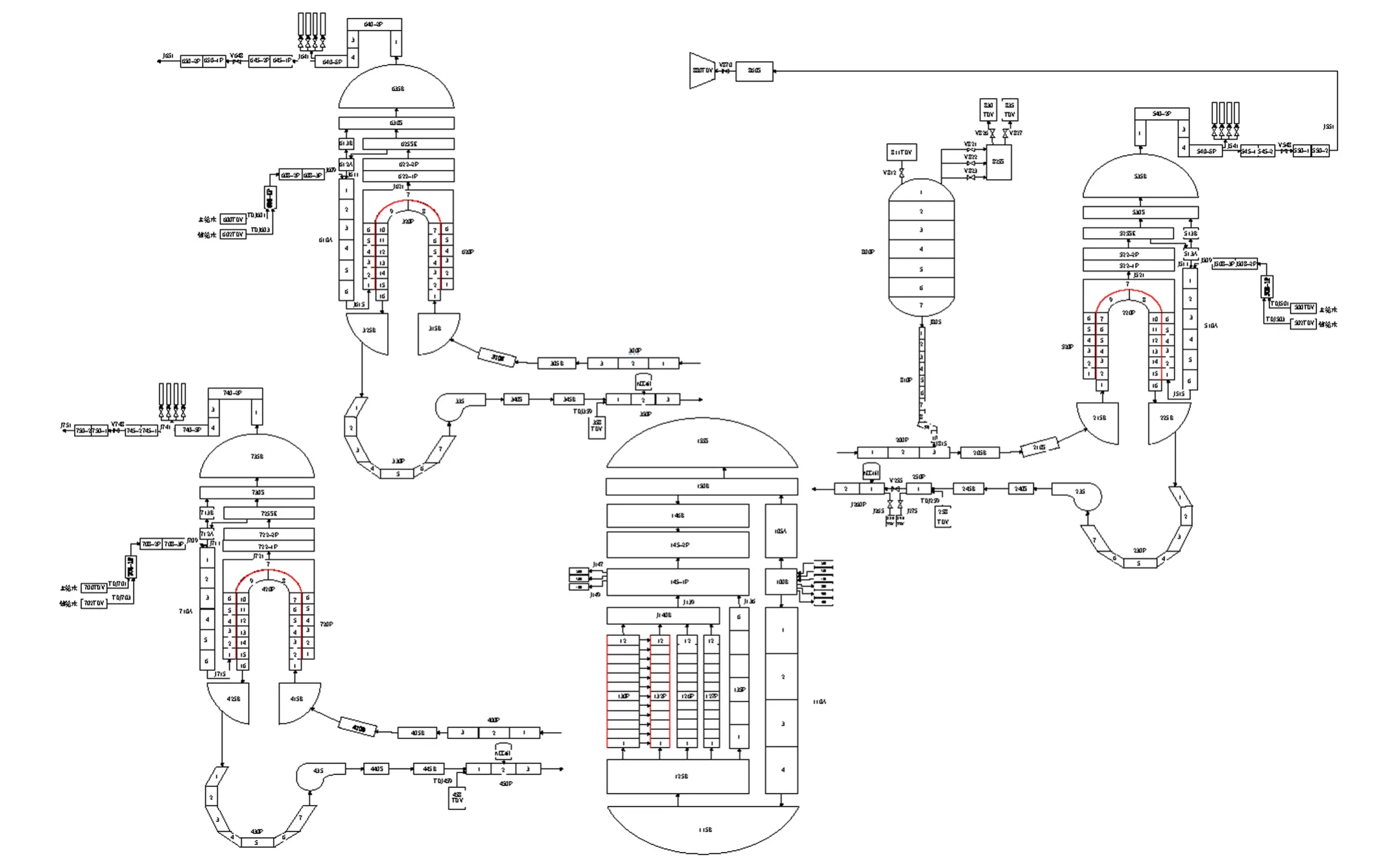
圖2 RELAP5 系統節點

1.3 穩態調試

在進行大破口失水事故瞬態計算之前，需要對建立的模型進行穩態調試，以確保各主要參數同電廠名義值一致。表1 為模型的穩態計算值和電廠名義值的相對偏差，從模型穩態計算結果可見，主要參數模型穩態計算值和名義值符合較好。

表1 模型穩態計算值相對偏差%

1.4 瞬態計算

模型在穩態運行1 000 s 后發生冷管段雙端剪切斷裂大破口失水事故，事故瞬態計算時間為300 s，大破口失水事故事件序列見表2。圖3—5 分別為大破口失水事故下歸一化堆芯功率、穩壓器壓力、破口總流量的模型計算曲線和參考曲線。從瞬態計算結果可見，計算曲線與參考曲線大小趨勢基本一致。

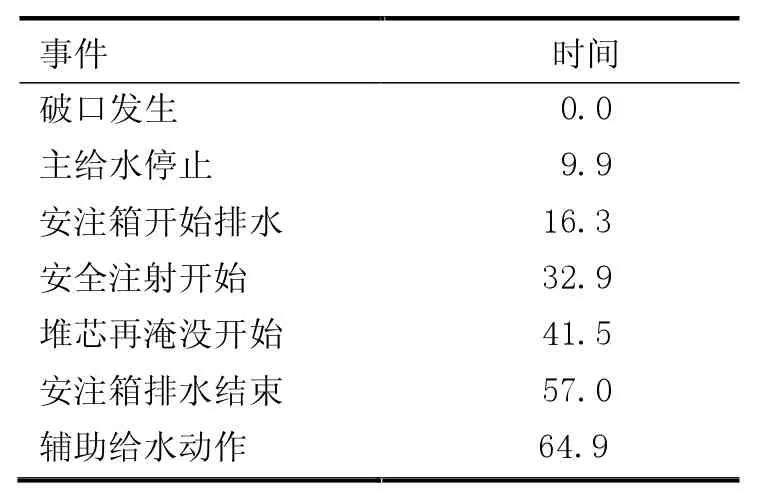
表2 大破口失水事故事件序列s

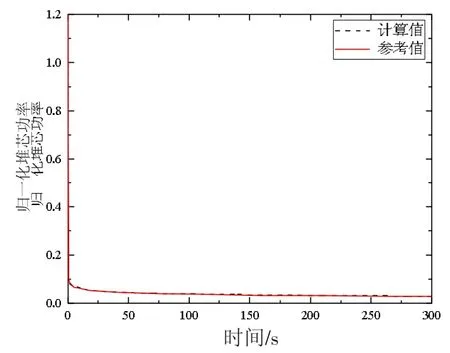
圖3 堆芯功率

圖4 穩壓器壓力

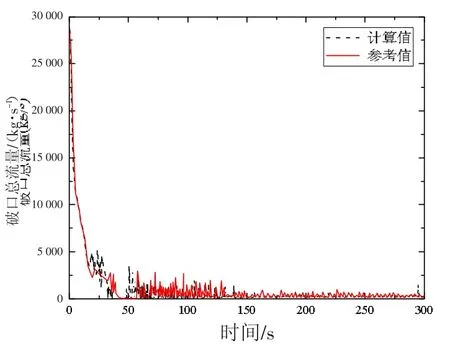
圖5 破口流量

2 理論方法

2.1 簡單隨機抽樣

2.1.1 均勻分布參數的簡單隨機抽樣

對于均勻分布參數，簡單隨機抽樣實現步驟如下。

1）通過公式（1）采用Python3.7 程序中的random 模塊調用random（）方法生成0 到1 之間的隨機浮點數u。

式中：random 為Python3.7 程序中的模塊，random（）為模塊中的方法。

2）通過公式（2）將隨機浮點數u映射為參數分布范圍內的隨機數。

式中：a為均勻分布參數的下限，b為均勻分布參數的上限。

2.1.2 正態分布參數的簡單隨機抽樣

對于正態分布參數，簡單隨機抽樣實現步驟如下。

1）通過公式（1）采用Python3.7 程序中的random 模塊調用random（）方法生成0 到1 之間的隨機浮點數u；

2）將u視為標準正態分布的分布函數值，采用公式（3）借助標準正態分布反函數映射到上1-u分位點z；

式中：z為標準正態分布的上1-u分位點，?-1為標準正態分布的反函數。

3）采用線性變換公式（4）將z映射為正態分布抽樣散點。

式中：σ 為正態分布的標準差，μ 為正態分布的期望值。

2.2 拉丁超立方抽樣

2.2.1 均勻分布參數的拉丁超立方抽樣

對于均勻分布參數，拉丁超立方抽樣[3]實現步驟如下。

1）將均勻分布參數的取值范圍等概率分割為滿足公式（5）的N個子區間；

式中：X為隨機變量，Ii為等概率區間坐標值。

2）采用公式（6）將0 到1 之間的隨機浮點數u映射為歸一化區間的各子區間的隨機數；

3）通過公式（7）將隨機數zi映射為參數分布范圍內的隨機數；

2.2.2 正態分布參數的拉丁超立方抽樣[3]

對于正態分布參數，拉丁超立方抽樣實現步驟如下。

1）依據公式（8）將正態分布參數區間進行等概率劃分

2）通過公式（9）將0 到1 之間的隨機浮點數u映射為歸一化區間的各子區間的隨機數；

3）將νi視為標準正態分布的分布函數值，采用公式（10）借助標準正態分布反函數映射到上1-νi分位點wi；

4）采用線性變換公式（11）將wi映射為正態分布抽樣散點。

2.3 Wilks 非參數統計

Wilks 非參數統計方法[4]廣泛應用于BEPU 統計分析中。基本思想是通過Wilks 公式根據選定的置信水平和概率水平獲取最小的計算次數，通過對響應參數的有序統計理論來獲取統計容忍區間。

對于概率密度分布函數g（y），確定一統計容忍區間（L，U），此區間對y的覆蓋率至少為γ 的概率為β，通過式（12）表示為

式中：β 為置信水平，γ 為概率水平，L為容忍下限，U為容忍上限，P為概率。

依據有序統計理論和多項式分布定律可推導出單側統計容忍區間Wilks 公式為

式中：N為計算次數。

Wilks 非參數統計方法具有黑箱統計模型的特點，由公式（13）可知：計算次數僅與置信水平和概率水平有關，與輸入變量的數量及其概率密度分布無關。Guba[5]在2003 年將單側統計容忍區間Wilks 公式推廣到下式

式中：p為輸出變量數量。

依據Wilks 非參數統計方法，采取95%置信水平和95%概率水平（簡記為95/95），若只有一個輸出變量，確定95/95 單側統計容忍上限至少需進行59 次運算，取59 次運算最大值；若計算次數為93 次，取次大值作為95/95 單側統計容忍上限；若計算次數為124次，取第三大值作為95/95 單側統計容忍上限。

3 不確定性量化與敏感性分析

3.1 輸入參數抽樣

主要依據大破口失水事故PIRT 表[6]，綜合考慮大破口失水事故過程中燃料棒、反應堆堆芯、換料水箱和安注箱等重要部件重要現象，識別大破口失水事故下對關鍵安全參數PCT 有重要影響的模型參數、電廠參數（電廠初始條件和電廠邊界條件），并結合相關資料等多種方式綜合確定不確定性輸入參數。選用的不確定性輸入參數見表3。對各種不確定性輸入參數的范圍和概率密度分布，結合核電站設計文件、已有的相關文獻資料及工程經驗判斷加以判定。在信息不足的情況下，不確定性輸入參數通常假設為均勻分布。

表3 不確定性輸入參數

采用Python3.7 程序調用Mersenne Twister 隨機數產生器。對不確定性輸入參數分別進行124 次簡單隨機抽樣和拉丁超立方抽樣。

可見抽樣散點反映了輸入參數的分布特征，對于均勻分布的輸入參數，散點在取值范圍內分布均勻。對于正態分布參數，散點分布呈現出中間聚集效應。拉丁超立方抽樣比簡單隨機抽樣散點分布更加均勻。以堆芯功率散點分布為例，簡單隨機抽樣相鄰散點距離的標準差為0.517 7，而拉丁超立方抽樣相鄰散點距離的標準差僅為0.252 6。

3.2 不確定性量化

將簡單隨機抽樣和拉丁超立方抽樣結果組合作為RELAP5/MOD3.4 程序輸入并執行計算，得到基于2 種抽樣的124 組熱點處燃料包殼溫度瞬態曲線。通過AptPlot 程序提取熱點處包殼峰值溫度數據。相應的包殼峰值溫度散點分布如圖6 和圖7 所示。

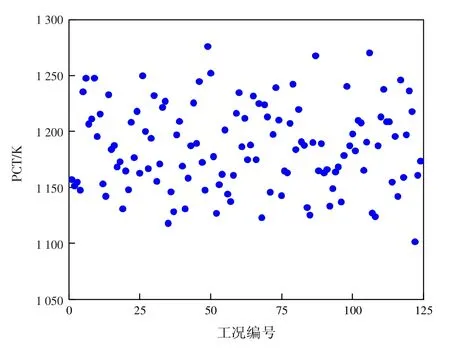
圖6 基于SRS 的124 組PCT 散點

圖7 基于LHS 的124 組PCT 散點圖

將124 組包殼峰值溫度由大到小進行排序，根據Wilks 非參數統計理論可知，排序第3 位的值即為包殼峰值溫度, 在95%置信水平上具有95%概率水平的單側統計容忍上限。基于簡單隨機抽樣計算得到包殼峰值溫度單側統計容忍上限95/95PCT 為1 264.057 K，基于拉丁超立方抽樣計算得到包殼峰值溫度單側統計容忍上限95/95PCT 為1 267.617 K。基于2 種抽樣方法得到的包殼峰值溫度，單側統計容忍上限均低于驗收準則規定的限值1 477 K。基于2 種抽樣方法得到的包殼峰值溫度單側統計容忍上限較為接近，僅相差3.56K。

3.3 敏感性分析

Spearman 秩相關系數法作為全局敏感性分析方法[7]，可檢驗多個輸入參數對響應參數的全局影響。采用Spearman 秩相關系數作為輸入參數對包殼峰值溫度敏感性的度量。Spearman 秩相關系數的絕對值大小表示敏感性強弱，其計算公式為

式中：RXi為Xi在X中的大小排序，RYi為Yi在Y中的大小排序。

基于簡單隨機抽樣和拉丁超立方抽樣的不確定性輸入參數與包殼峰值溫度間的Spearman 秩相關系數如圖8 和圖9 所示。

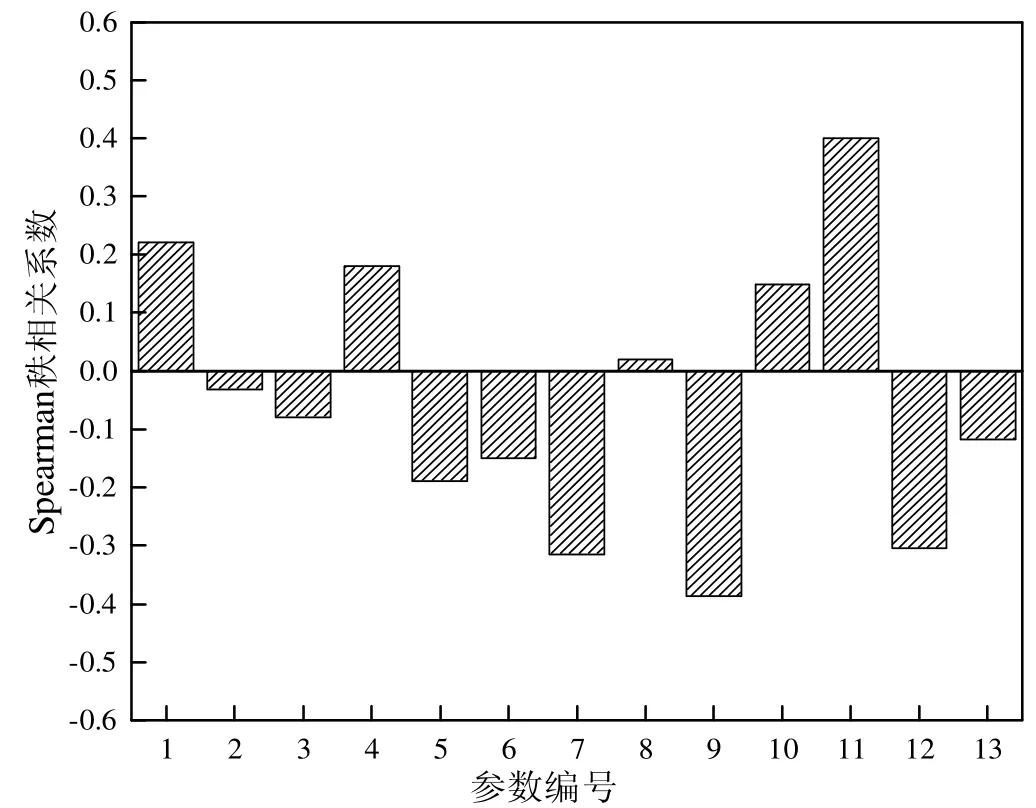
圖8 基于SRS 輸入參數的Spearman 秩相關系數

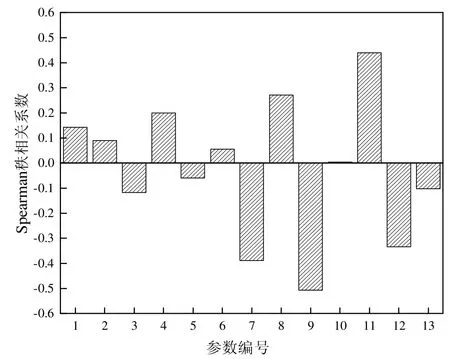
圖9 基于LHS 輸入參數的Spearman 秩相關系數

基于簡單隨機抽樣的敏感性分析結果表明包殼峰值溫度對衰變熱、換料水箱水溫、安注箱水溫和氣隙導熱率較為敏感；基于拉丁超立方抽樣的敏感性分析結果表明，包殼峰值溫度對衰變熱、換料水箱水溫、安注箱水溫和氣隙導熱率較為敏感。因此采用Spearman 秩相關系數法基于2 種不同的抽樣方法識別出的包殼峰值溫度四大主要影響參數相一致。

4 結論

以百萬千瓦級壓水堆核電廠大破口失水事故為分析對象，基于簡單隨機抽樣和拉丁超立方抽樣對包殼峰值溫度開展不確定性量化和敏感性分析計算，得到的結論如下。

1）采用簡單隨機抽樣和拉丁超立方抽樣對不確定性輸入參數開展隨機抽樣，拉丁超立方抽樣散點比簡單隨機抽樣散點分布更加均勻，能夠更好地復現參數的分布特征。

2）采用Wilks 非參數統計理論基于簡單隨機抽樣和拉丁超立方抽樣計算得到的95/95 PCT 均滿足ECCS 驗收準則，且95/95 PCT 非常接近，僅相差3.56 K。

3）采用Spearman 秩相關系數法基于簡單隨機抽樣和拉丁超立方抽樣均識別出包殼峰值溫度對衰變熱、換料水箱水溫、安注箱水溫和氣隙導熱率較為敏感。