基于Bellman原理的人員密集場所疏散路徑優化研究

王 勇，李肖肖，鄒成祥，李亞萍

（武漢科技大學 資源與環境工程學院，湖北 武漢 430081）

0 引言

人員密集場所具有人員流動性較強、人員數量和密度大等特點［1］，極易發生擁堵踩踏事故造成人員、財產損失，如“上海12·31 外灘踩踏事故”、“印度10·13 寺廟踩踏事故”［2］。隨著我國城市化進程的加快，有多部疏散樓梯、多條穿行通道的建筑和公共場所越來越多，這類建筑或場所的人員疏散過程存在多個決策點，可行性疏散路線較多，合理規劃疏散路徑可以引導人流，避免或緩解局部擁堵，減少疏散時間，對于提高人員疏散效率、保證生命財產安全具有重要意義［3］。

1 相關研究

目前，國內外學者對人員疏散及其路徑優化進行了大量研究。例如，楊樂等［4］針對傳統蟻群算法收斂速度慢、搜索時間長、易陷入局部最優等缺點，在其基礎上重新定義信息素更新方式，對搜索出的最短路徑進行平滑優化處理，使其能快速有效地搜索出最優路徑；趙曉東等［5］采用Java 語言設計并實現了給定條件下基于偏好的有向圖路徑搜索系統，在該系統中，用戶可基于偏好輸入相關數據得到想要的路徑集合，進而從中篩選出最優路徑；霍非舟等［6］研究視野受限條件下行人間信息傳遞對疏散時間的影響，并建立了考慮信息傳遞的人員疏散元胞自動機模型；謝啟苗等［7］建立了一種基于元胞自動機與改進囚徒困境模型的人員疏散仿真模型，并運用該模型考察恐慌心理對人員疏散路徑的影響；杜寶江等［8］采用Pyrosim 軟件動態模擬火災情況并輸出環境參數，通過改進當量長度代替蟻群優化算法中的幾何長度，同時改進目標函數，根據火場環境對信息素揮發系數進行動態更新。仿真實驗模擬了火災發展3個時期的路徑優化情況，驗證了該算法的有效性和收斂性；袁文濤等［9］在研究一般物流配送路徑問題處理方法和數學模型的基礎上提出一種改進蟻群算法以提高構建路徑的速度和質量，在限量車輛路徑問題中采用改進算法優化求解車物流的配送路徑；言娟等［10］設計了基于時空擁擠度與建筑信息模型的應急疏散路徑優化方法，解決了傳統建筑應急疏散路徑優化合理度低的問題；張佳瑜等［11］通過實地調查、查閱資料和影像數據，運用地理信息系統對避震疏散空間需求及路徑進行優化；萬遠等［12］通過引入路徑尋優方法、改進社會力模型、更新的啟發函數和信息素構建了新的行人路徑選擇與優化機制；Hong等［13］提出基于社會力模型與改進人工蜂群算法的應急疏散路徑規劃方法；Khalid 等［14］利用動態人群模型與基于免疫的路由機制解決緊急路線規劃問題；Nishaben 等［15］提出前向—后向最短路徑算法，以圖論為基礎對多條路徑進行組合，以確定精準的應急疏散路徑；Min 等［16］提出一種改進量子蟻群算法，采用量子比特表示螞蟻當前的信息素信息，采用量子旋轉門更新信息素信息，該算法可更快找到疏散方案，并且具有較強的魯棒性；徐橙瑋等［17］建立空間多目標優化模型，并采用多目標遺傳算法求解出最優疏散路徑；Hui 等［18］利用A*算法計算出實際路徑，提出針對建筑內部區域的3D 疏散路徑模型，規劃出最佳路徑。

以上研究主要通過建立模型、改進算法或引入最短路徑算法規劃疏散路徑，計算過程較為復雜。目前已有一些疏散模擬軟件能快速分析出人員疏散的最佳路徑和時間，減少人員傷亡，如STEPS、SGEM、Pathfinder 等，但均存在一定缺陷。例如，Pathfinder 軟件內嵌的局部最快算法以總時間最短為目標選擇疏散路徑，對當前房間不僅考慮運動時間而且考慮由于擁堵造成的排隊等候時間，但總時間中忽略了后續房間的排隊等候時間，僅以距離與最快速度的比值來預估后續房間的疏散時間［19］，這必將導致該算法不適用于后續房間內存在擁堵的情況。為此，本文以存在多步決策情形的某學生公寓人員疏散為例展開研究，針對Pathfinder 軟件模擬結果存在路徑利用率不均衡的問題，提出一種基于疏散模擬軟件的可代數求解的全局路徑優化方法。該方法基于決策點構建可行路徑模型，通過綜合路徑長度、疏散速度和局部最短疏散時間等因素，以總疏散時間最短為目標建立路徑優化模型，并基于Bellman 原理進行求解，最終確定最優路徑和疏散時間。

2 Pathfinder軟件模擬與分析

2.1 學生公寓模擬模型

通過Pathfinder 軟件建立的某學生公寓三維模型如圖1 所示。該公寓共7 層，1 層有40 間宿舍，2-7 層均有42 間宿舍，每間宿舍容納4 人。公寓內部的東西兩側各有一部疏散樓梯，樓梯凈寬度均為1.8 m；各層房間門凈寬度為0.9 m；疏散廊道通行無障礙物，凈寬度為1.8 m。公寓共有P1、P2、P33 個安全出口，寬度分別為2 m、2 m、1.2 m。Ma1、Ma2分別為第a+1 層下行到第a 層廊道的西側、東側樓梯口。

Fig.1 3-dimensional model of the student apartment圖1 學生公寓三維模型圖

模型主要參數包括：①人員速度設置。參照文獻［20］，將公寓疏散人員的運動速度設定為1.4 m/s；②人員行為與參數設置。人員均采用就近原則選擇出口進行疏散，疏散行為模式選用Steering 模式；人員行為設置為自行尋找任意安全出口（Go to Any Exit）；當前門偏好值（Current Door Preference，CDP）及當前房間距離懲罰值（Current Room Distance Penalty，CRDP）均取默認值35。

2.2 模擬結果分析

2.2.1 實時流率與累計人員數量分析

模擬得到的實時流率曲線和累計人員數量分別如圖2、圖3 所示。由圖2 可知，M11的使用時段為6.5-253.5 s，總利用時長為247 s；M12的使用時段為5.5-327.5 s，總利用時長為322 s，M12的 總利用時 長比M11多75 s。由圖3 可知，通過M11疏散的總人數為435 人，通過M12疏散的總人數為573 人，通過M12疏散的人數比M11多138 人。在疏散過程中，東、西側樓梯的使用情況不均衡。

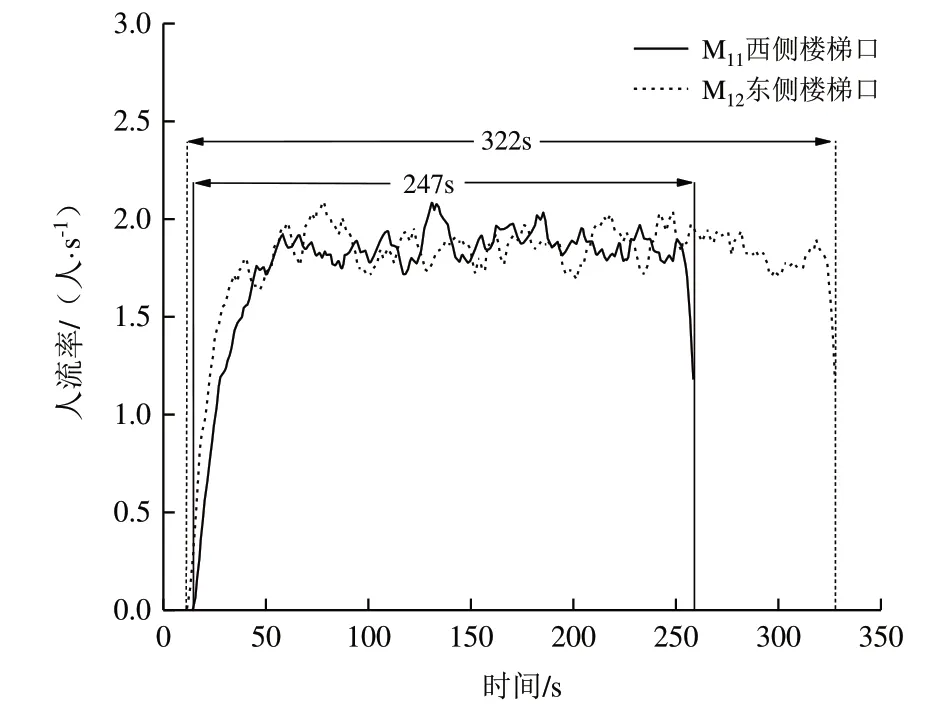
Fig.2 Real-time flow rate curves of M11 and M12圖2 M11、M12實時流率曲線

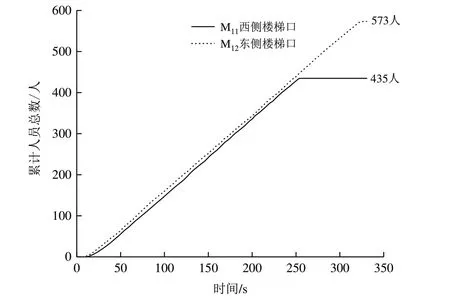
Fig.3 Total number of person passing through M11 and M12圖3 通過M11、M12的累計人員數量

2.2.2 模型參數優化分析

由表1 可知，CRDP、CDP 取默認值，總疏散時間為330.3 s。若CRDP=35 m，總疏散時間會隨著CDP 參數值的減小而單調減小，CDP 參數取0 為較佳值；若CDP=0，總疏散時間會隨著CRDP 參數值的減小而先增大后減小然后再增大，CRDP 參數取35 為較佳值。即使設定CRDP=35 m，CDP=0，經過東西兩側樓梯的人數差值仍為62 人，兩側樓梯的使用情況仍存在較大差異，說明軟件本身優化效果不足。

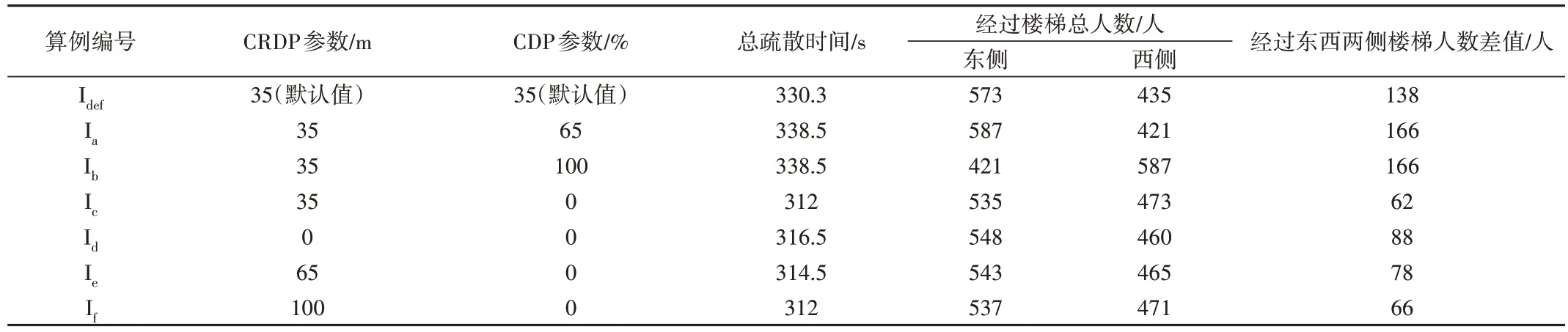
Table 1 Effects of main model parameters on the simulation results表1 主要模型參數對模擬結果的影響

3 學生公寓全局路徑優化

在保證疏散路徑安全的基礎上，本文提出一種以總疏散時間最短為目標的路徑優化方法，詳細流程見圖4。

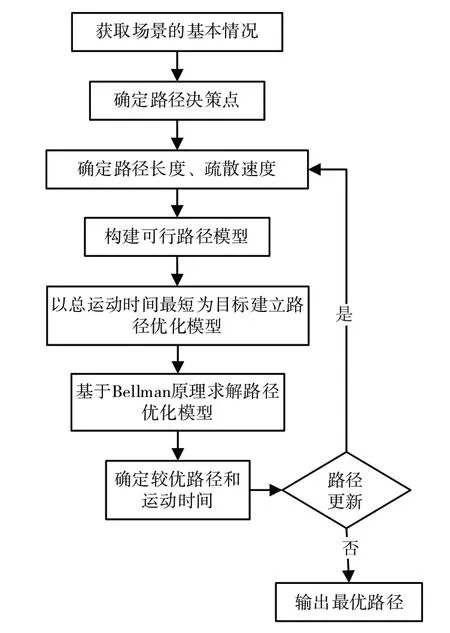
Fig.4 Path optimization flow圖4 路徑優化流程

3.1 決策點確定及可行路徑模型構建

學生公寓的可行路徑模型如圖5 所示。第i 層樓的任一房間門Ci及樓梯口Ma1、Ma2構成路徑決策點。線段上的數字表示決策點之間的路徑長度，各樓層房間門至下一決策點的具體路徑長度如表2、表3所示。

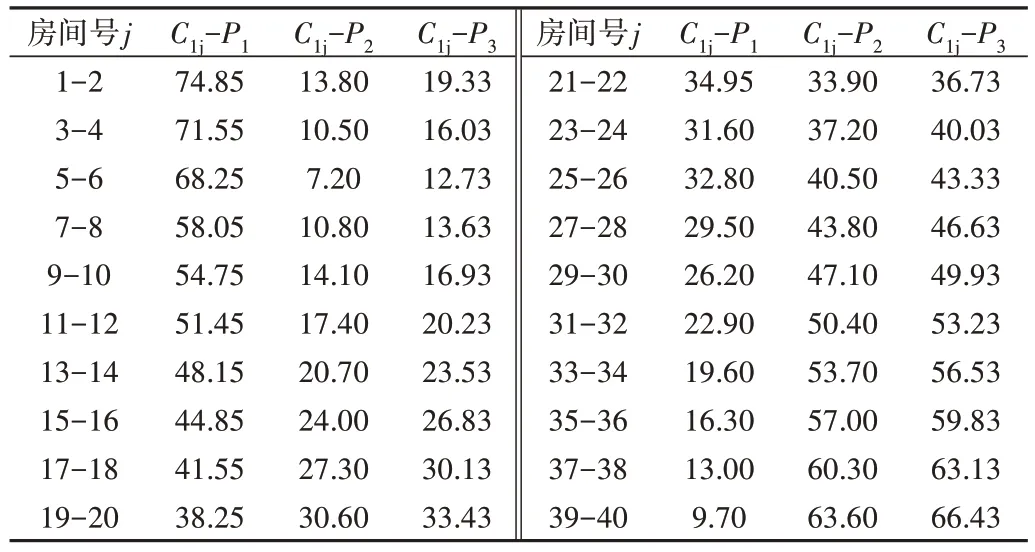
Table 2 Path length from C1j to P1，P2 and P3 of the first floor表2 第1層樓房間門Cij至P1、P2及P3的路徑長度（m)

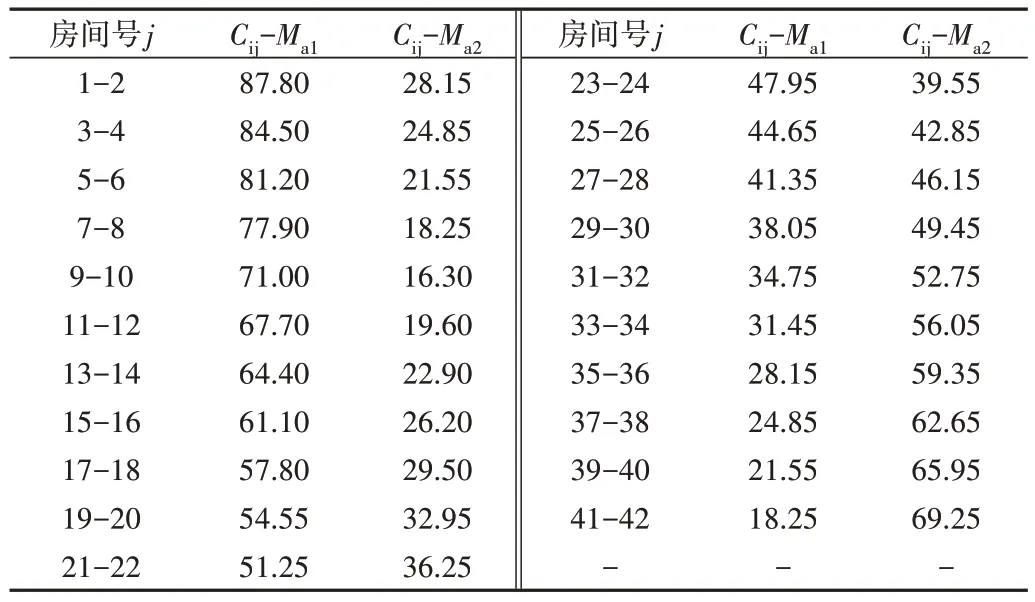
Table 3 Path length from Cij to Ma1 and Ma2 of the floor of 2-7表3 第2-7層各房間門Cij至Ma1、Ma2的路徑長度（m，i≥2，a=i-1）

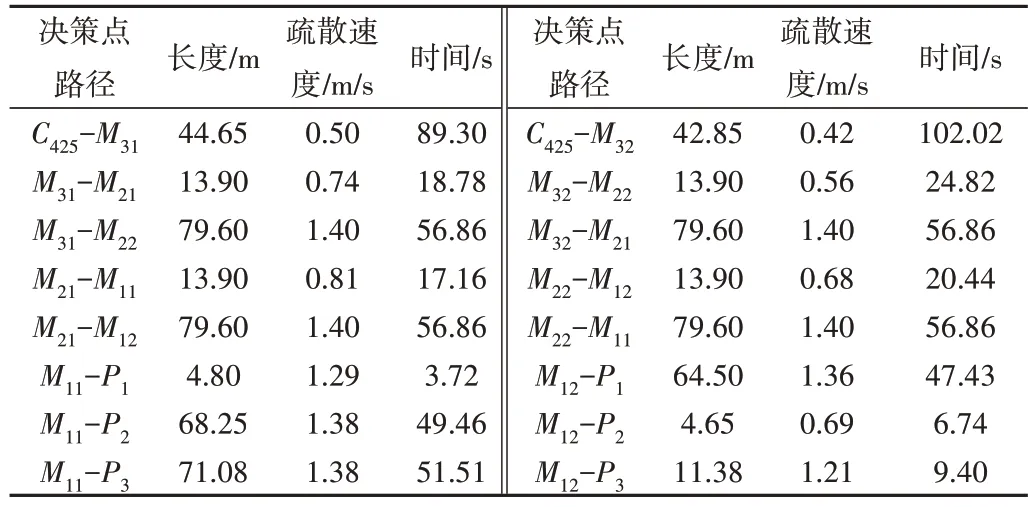
Table 4 Path length，evacuation speed and time of decision nodes between exit and room 425表4 房間門C425至出口各決策點之間的路徑長度、疏散速度及時間

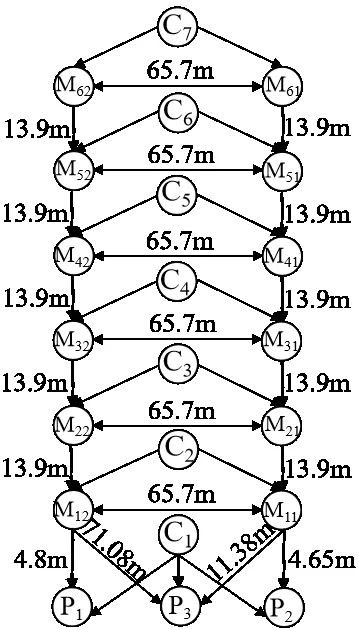
Fig.5 Feasible path model for the student apartment圖5 學生公寓可行路徑模型

3.2 路徑優化模型建立與求解

3.2.1 路徑優化模型建立

針對第k階段的疏散路徑優化目標函數為：

式中：k為階段變量，k=1，2，…，N；gk為階段指標函數，以疏散時間為階段指標，其為路徑長度和疏散速度的函數，即gk=tk=L/V，其中tk為第k階段所需疏散時間；L為第k階段決策點與決策點之間的路徑長度，m；V為第k階段決策點與決策點之間的疏散速度，m/s；Sk為狀態變量，用于描述各階段的狀態，包括第k+1階段的決策；dk～N為第k階段到第N 階段的決策。一般情況下，第N階段的輸出狀態SN+1已經不再影響本過程的策略，即式中的邊界條件fN+1（SN+1）=0。

3.2.2 路徑優化模型求解

Bellman 原理為在最優策略的任意一階段上，無論過去狀態和決策如何，對過去決策所形成的當前狀態而言，余下的諸決策必須構成最優子策略。基于該原理，可逆序對路徑優化目標函數進行求解，即從最后階段開始逐步向前逆向尋求最短疏散時間。首先求解最后一個階段的優化目標函數fN（SN），得到該階段的局部優化決策；然后基于該階段的決策結果繼續求得fN-1（SN-1）所對應的局部優化決策，依此類推，直至求得目標函數f1（S1）所對應的局部優化決策；最后將各局部優化決策整合得到全局優化決策。

3.3 疏散路徑優化過程及效果分析

3.3.1 路徑優化過程

以公寓第4 層樓25 號（425）房間、第5 層樓23 號（523）房間優化過程為例，其疏散路徑優化決策如圖6、圖7 所示。圖中決策點之間各可行路徑線段上的數字為疏散時間，其求解所依據的路徑長度、疏散速度見4、表5，其中疏散速度來自Pathfinder模擬結果。

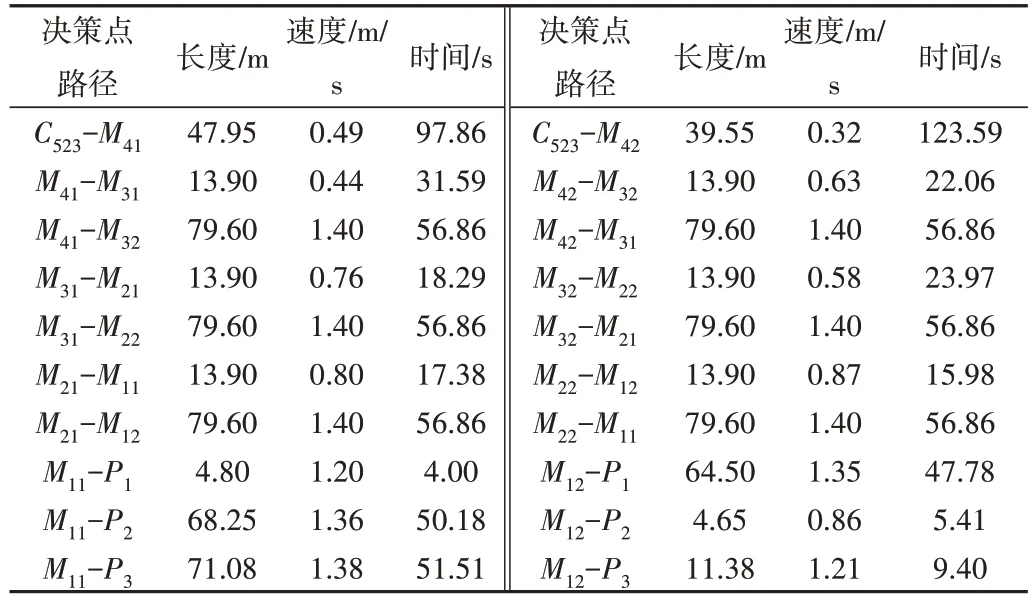
Table 5 Path length，evacuation speed and time of decision nodes between exit and room 523表5 房間門C523至出口各決策點之間的路徑長度、疏散速度及時間

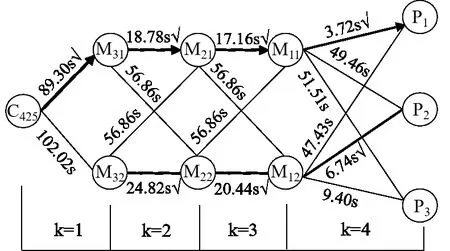
Fig.6 Evacuation path optimization decision for room 425圖6 425房間疏散路徑優化決策

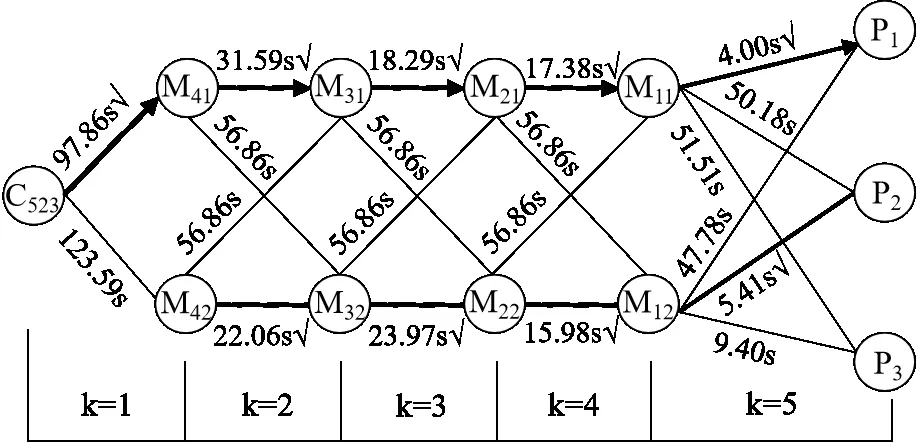
Fig.7 Evacuation path optimization decision for room 523圖7 523房間疏散路徑優化決策

425 房間的路徑決策過程可劃分為4 個階段，即階段變量k=1、2、3、4。基于Bellman 原理，從最后階段開始逆序尋求最短疏散時間。首先從階段k=4 開始，選出該階段中各決策點之間的最短疏散時間路徑，即路徑M11-P1；其次，選出階段k=3 中各決策點之間的最短疏散時間路徑，即路徑M21-M11；然后選出階段k=2 中各決策點之間的最短疏散時間路徑，即路徑M31-M21；最后選出第一階段k=1 中各決策點之間的最短疏散時間路徑，即路徑C425-M31。最終得到425 房間的最優疏散路徑為C425→M31→M21→M11→P1。同理，523 房間的最優疏散路徑為C523→M41→M31→M21→M11→P1。運用優化方法一次運算即得學生公寓所有房間的最優疏散路徑（見表6），按該優化路徑設置后Pathfinder模擬的公寓人員總疏散時間為292.3 s。

Table 6 Optimal evacuation routes for all rooms表6 所有房間最優疏散路徑

3.3.2 優化效果分析

（1）總疏散時間分析。設置優化路徑后的模擬結果與原模擬結果相比，公寓的總疏散時間從330.3 s 減少至292.3s。

（2）優化后實時流量與累計人員數量分析。圖8 為優化后的實時流量曲線圖。可以看出，M11的使用時段為6.5-288.5 s，總利用時長為282 s；M12的使用時段為5-288.5 s，總利用時長為283.5 s。圖9 為優化后的累計人員數量圖，可以看出，通過M11、M12疏散的總人數均為504人，優化后東、西側樓梯的利用率相當，公寓整體疏散效率達到最高。

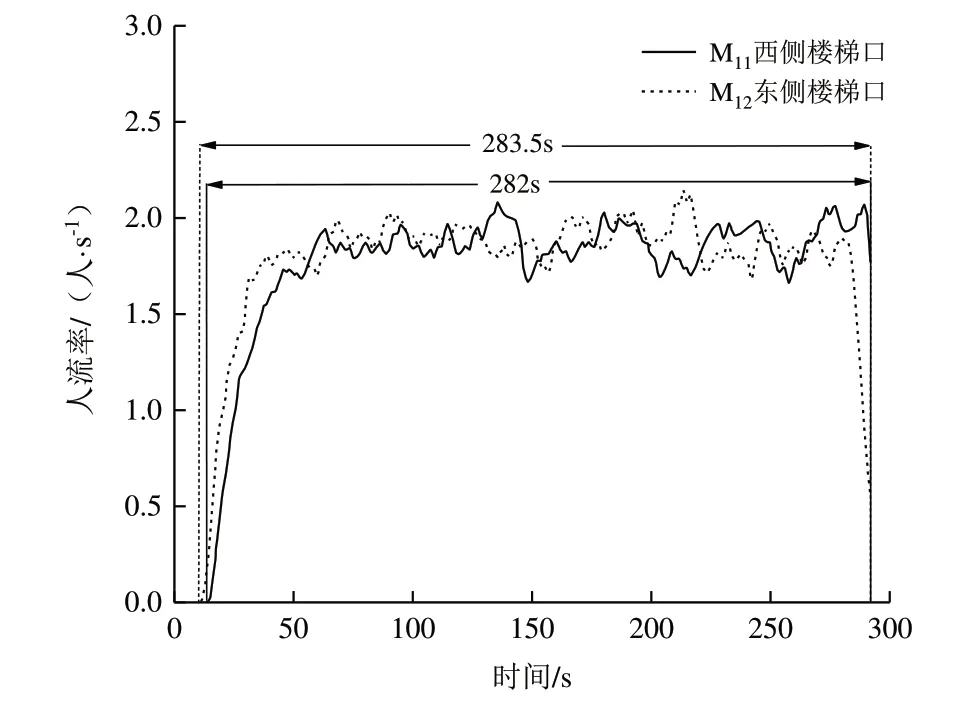
Fig.8 Optimized real-time flow rate curves圖8 優化后實時流率曲線

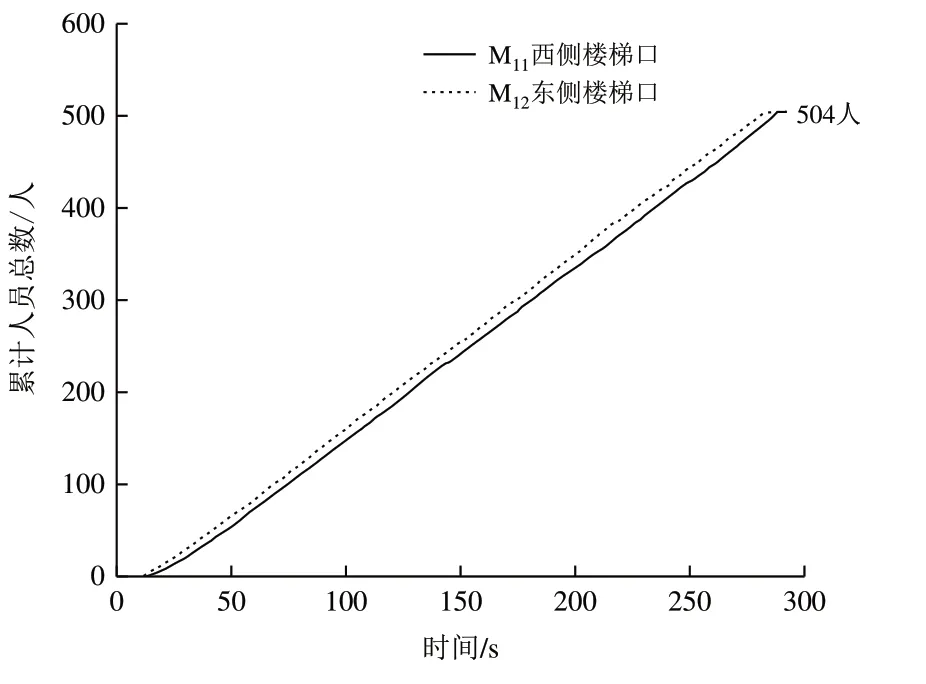
Fig.9 Total number of accumulated person after optimization圖9 優化后累計人員數量

4 結語

Pathfinder 軟件對學生公寓人員疏散過程的模擬結果表明，東西兩側樓梯的使用情況不均衡，調整模型主要參數為最佳值，即CDP=0、CRDP=35m，此時經過東西兩側樓梯的總人數仍相差62 人，說明軟件內嵌的局部最快算法在多決策點密集群體疏散方面存在缺陷，軟件本身優化效果不足。為此，本文以總疏散時間最短為目標，在軟件模擬結果的基礎上確定決策點，以可行路徑模型圖的方式展現出全局路徑，同時通過Bellman 原理簡單快捷地代數求解出優化路徑，最終得到全局最優疏散方案。路徑優化后的模擬結果與原模擬結果相比，總疏散時間縮短了38 s，東側樓梯處部分人流量被分散至西側樓梯處，東西兩側樓梯的利用情況達到均衡狀態。然而，本文設置的人員疏散情景為緊急疏散，未耦合火災、地震等具體危險場景。后續研究中可引入火災情景進行人員疏散，并根據災害發生地點給不同路徑賦予不同的危險度，以區別其可通過程度。通過程序設計，將所提出的全局最優路徑優化方法代碼化，形成獨立于Pathfinder 軟件的疏散路徑優化工具，或對Pathfinder軟件進行二次開發賦予其路徑優化功能。