基于多種群遺傳算法的鋼框架結構優化設計

周俊文　劉界鵬

摘要：傳統的基于力學分析軟件的結構設計方法存在效率低下、依靠專家經驗等局限性，采用智能算法能實現高效的結構自動優化設計。然而，由于隨機搜索特征，優化結果和收斂性高度依賴于算法的參數設置，需要通過試算來確定其合理取值，該方法會造成優化效率低、計算量大等問題。引入多種群協作和信息共享機制來改善此類問題，并研究其在結構優化設計中的適用性。利用MSC.Marc軟件建立鋼框架結構有限元模型，采用底部剪力法將地震作用等效為水平荷載施加到結構上，搭建有限元軟件與智能算法的自動優化過程，以結構的總體材料用量最低為目標，考慮了層間位移角、應力比、構件穩定性和寬厚比等多種約束條件，以遺傳算法為基礎，通過適應度尺度變換、基于方向的交叉算子、非均勻變異算子、自適應概率、精英保留策略、重復項替代機制、基于約束的策略對其進行改進，引入多種群思想，對比多種算法優化結果的差異。結果表明：基于多種群的遺傳算法能有效改善優化結果對算法參數的依賴性，提高結構優化設計的效率。

關鍵詞：鋼框架結構；結構優化設計；多種群遺傳算法；智能算法

中圖分類號：TU318；TU392.1? ? ?文獻標志碼：A? ? ?文章編號：2096-6717（2024）01-0071-11

Optimization design of steel frame structure based on multi-population genetic algorithm

ZHOU Junwen， LIU Jiepeng

（School of Civil Engineering； Key Laboratory of New Technology for Construction of Cities in Mountain Area of Ministry of Education， Chongqing University， Chongqing 400045， P. R. China）

Abstract： The traditional structural design method based on mechanical analysis software has some limitations， such as low efficiency and expert experience reliance. The efficient automatic structural optimization design can be achieved by using intelligent algorithms. However， due to the random search feature， the optimization result and convergence are highly dependent on the parameter settings of the algorithm whose reasonable values need to be determined by the trial-and-error procedure. It results in inefficient optimization and substantial computational cost. Therefore， this paper introduces the multi-population collaboration and information sharing mechanism to improve such problems and its applicability in the structural optimization design is studied. The finite element model of a steel frame is built by MSC.Marc and the equivalent horizontal load from earthquake obtained by base shear method is exerted on the structure. The automatic optimization process is established based on finite element software and the intelligent algorithm with the aim of mininizing the total material cost of the structure. Multiple structural constraints are considered including the inter-story drift ratio， the stress ratio， and the stability and width-thickness ratio of the component. Several strategies are used to improve the performance of the genetic algorithm， such as the fitness scaling， the direction-based crossover operator， the non-uniform mutation operator， the adaptive probability， the elite strategy， the duplicate substitution mechanism， and the constraint-based strategy. Then the multi-population mechanism is introduced to such an algorithm. The results of different algorithms are compared with each other， which shows that the multi-population genetic algorithm can improve the dependence of optimization results on algorithm parameters and the efficiency of structural optimization design.

Keywords： steel frame structure； structural optimization design； multi-population genetic algorithm； intelligent algorithms

中國位于地震多發帶，受地震作用的影響，大量建筑物被損毀，造成了巨大的經濟損失和人員傷亡[1-3]。據建筑業發展報告統計，2021年上半年，中國建筑業企業完成建筑業總產值119 843.55億元，同比增長18.85%，呈現出蓬勃向上的發展趨勢，建筑結構的安全性和經濟性成為重要的關注點。因此，研究高效的建筑結構設計方法，對保證建筑行業的快速發展具有重要的現實意義。

傳統的建筑結構設計方法主要依賴PKPM等設計軟件的力學計算分析結果，憑借專家經驗對結構進行人為調整，包括合理的構件布置和截面取值等，使其滿足相關規范的要求，以實現優化設計，在保證結構安全性的同時降低建筑材料成本[4-8]，該方法受人為主觀因素的影響較大且耗時耗力，已無法滿足建筑行業快速發展的需求。以智能化方法實現結構的自動建模分析和優化設計，能有效改善傳統結構設計效率低下的問題，并保證優化后結構的經濟有效性[9-12]。

與傳統的混凝土結構、砌體結構相比，鋼框架結構具有輕質高強、延性好、結構形式簡單、施工方便等優點，應推廣其在地震區的應用[1]，近年來，在鋼框架結構的智能優化設計方面已有大量學者進行了相關研究。Degertekin等[13]考慮截面選型和位移約束，采用和聲搜索算法對鋼框架進行了優化設計，降低了鋼框架的重量。Gholizadeh[14-15]采用智能算法對平面鋼框架結構進行了優化設計，包括蝙蝠算法和海豚回聲算法，研究了結構尺寸的優化，實現了結構總質量的降低，研究了剪力墻位置的優化，得到了最優布局。Talatahari等[16]采用基于差分進化的鷹策略算法，?arba?[17]采用基于生物地理學的優化算法，Kaveh等[18]采用先進的充電系統搜索算法對鋼框架結構進行優化，優化后的結構能夠滿足約束限值的要求，其材料總成本得到了有效地降低。智能算法已在結構優化的研究中有了廣泛的應用，在每次優化過程中，需要首先對算法參數進行相應的設置，當其取值不合理時，容易會引起算法的收斂性和優化結果的優異性等問題，造成計算量大、耗時長、結果不理想、隨機性強等后果，如遺傳算法中的變異概率，當其設定較大時，容易破壞原有優秀個體的基因，當其設定較小時，可能使優化陷入局部最優解而過早收斂。在單次優化過程中，引入多種群的概念，每個種群設置不同參數值而表現出不同的優化性能，通過信息共享來進行不同種群間的交流，從而發揮多種群算法的綜合性能優勢，能夠有效提高搜索能力，降低優化結果對參數設置的依賴性[19-20]。基于多種群思想的算法在優化問題中存在一定的優勢，已應用到兵工、計算機等領域[21-22]，然而其在土木工程領域的應用仍有限。對于建筑結構設計而言，優化問題比較復雜，涉及非凸性、非線性、變量離散性、局部最優解眾多等，優化對象存在較大的結構差異和較強的構件相互作用，且優化結果和收斂性高度依賴于算法的更新機制和搜索能力，因此，在實現高效的結構優化設計方面，該算法的適用性仍有待研究。

目前，中國正在大力推進經濟有效結構的發展，以最小的資源和成本，造出外觀美、空間分布合理并滿足安全性要求的建筑物，實現資源的最大化利用和經濟性。筆者以遺傳算法為基礎，通過多種策略對其進行改進并引入多種群思想，將其應用于鋼框架結構的優化問題中，以驗證方法的有效性，旨在為鋼框架結構的優化設計提供參考。

1 優化問題

1.1 優化對象

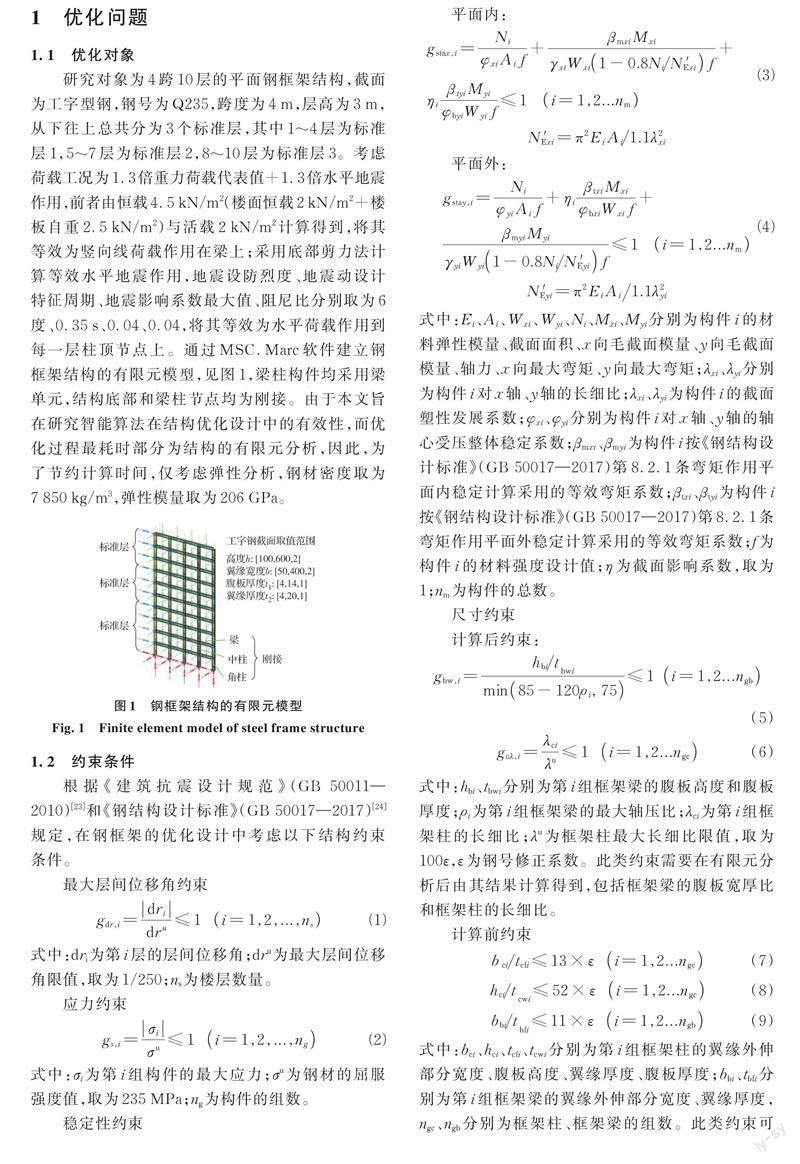
研究對象為4跨10層的平面鋼框架結構，截面為工字型鋼，鋼號為Q235，跨度為4 m，層高為3 m，從下往上總共分為3個標準層，其中1～4層為標準層1，5～7層為標準層2，8～10層為標準層3。考慮荷載工況為1.3倍重力荷載代表值+1.3倍水平地震作用，前者由恒載4.5 kN/m2（樓面恒載2 kN/m2+樓板自重2.5 kN/m2）與活載2 kN/m2計算得到，將其等效為豎向線荷載作用在梁上；采用底部剪力法計算等效水平地震作用，地震設防烈度、地震動設計特征周期、地震影響系數最大值、阻尼比分別取為6度、0.35 s、0.04、0.04，將其等效為水平荷載作用到每一層柱頂節點上。通過MSC.Marc軟件建立鋼框架結構的有限元模型，見圖1，梁柱構件均采用梁單元，結構底部和梁柱節點均為剛接。由于本文旨在研究智能算法在結構優化設計中的有效性，而優化過程最耗時部分為結構的有限元分析，因此，為了節約計算時間，僅考慮彈性分析，鋼材密度取為7 850 kg/m3，彈性模量取為206 GPa。

1.2 約束條件

根據《建筑抗震設計規范》（GB 50011—2010）[23]和《鋼結構設計標準》（GB 50017—2017）[24]規定，在鋼框架的優化設計中考慮以下結構約束條件。

最大層間位移角約束

式中：Ei、Ai、Wxi、Wyi、Ni、Mxi、Myi分別為構件i的材料彈性模量、截面面積、x向毛截面模量、y向毛截面模量、軸力、x向最大彎矩、y向最大彎矩；λxi、λyi分別為構件i對x軸、y軸的長細比；λxi、λyi為構件i的截面塑性發展系數；φxi、φyi分別為構件i對x軸、y軸的軸心受壓整體穩定系數；βmxi、βmyi為構件i按《鋼結構設計標準》（GB 50017—2017）第8.2.1條彎矩作用平面內穩定計算采用的等效彎矩系數；βtxi、βtyi為構件i按《鋼結構設計標準》（GB 50017—2017）第8.2.1條彎矩作用平面外穩定計算采用的等效彎矩系數；f為構件i的材料強度設計值；η為截面影響系數，取為1；nm為構件的總數。

式中：bci、hci、tcfi、tcwi分別為第i組框架柱的翼緣外伸部分寬度、腹板高度、翼緣厚度、腹板厚度；bbi、tbfi分別為第i組框架梁的翼緣外伸部分寬度、翼緣厚度，ngc、ngb分別為框架柱、框架梁的組數。此類約束可以在進行有限元分析前計算得到，包括框架柱的翼緣外伸部分和腹板寬厚比、框架梁的翼緣外伸部分寬厚比。

2 優化方法

2.1 設計變量

如圖1所示，鋼框架結構總共設有3個標準層，將每個標準層中的構件劃分3組，包括角柱、中柱和梁，總共有9組構件，每組構件設置4個參數，包括工字型鋼截面的翼緣寬度b、總高度h、腹板厚度t1、翼緣厚度t2，記為（b、h、t1、t2），單位為mm，因此，該優化問題中總共考慮36個設計變量，變量的取值范圍見表1。

2.2 目標函數

以結構的鋼材總質量最小化為目標函數，包括所有的框架梁柱構件，其數學表達式為

當結構滿足所有的約束條件時，式（12）第2項為0，偽目標函數等于結構總質量；當結構存在約束超限的情況時，式（12）第2項將遠大于0，偽目標函數大于結構總質量。因此，偽目標函數值越小，則結構更好，其既能滿足所有的約束條件，又能實現經濟性。

偽目標函數是一項考慮結構原始總質量和所有約束條件的綜合指標，可以將有強約束的結構優化設計問題轉換為無約束問題，通過種群個體函數值之間的對比，能夠反映出結構違反約束條件的程度、超限數量、材料質量和結構相對優劣等信息，以實現對個體的比較選擇。

2.3 優化算法

以遺傳算法為基礎，引入多種改進策略和多種群思想，結合結構和設計變量特征，基于規范要求對鋼框架結構進行優化設計，旨在說明多種群遺傳算法的有效性。采用的所有算法都具有相同的種群初始化、適應度評估步驟，在設計變量生成和更新時都采用了基于約束的策略，將先對其進行統一描述。

基于約束的策略見圖2。遺傳算法是一種隨機性較強的算法，在初始化和迭代過程中生成種群時不具有方向性，通常存在新個體無法滿足約束條件或原本滿足要求的個體在變量更新后出現超限的情況，這會增加無效個體（存在超限情況的個體）的數量，從而導致計算時間的增加。為了減少該情況發生的可能性，以構件組為單位，采用基于約束的策略來改善該問題，僅針對計算前約束條件。在初始化過程中或在迭代過程中通過交叉、變異操作后，當有新個體生成時，遍歷每個構件組，均通過式（7）～式（9）對其截面參數進行相關驗算，當滿足要求時，該構件組生成有效，否則重復進行相同操作，直至滿足要求為止，為了避免某些構件組始終無法滿足要求而陷入死循環的情況，設置最大重復操作的次數，在超過30次后，將該構件組的4個參數在取值范圍內重新隨機生成，直到滿足要求。該策略將應用于包括種群初始化、交叉、變異、重生成等所有會生成新個體的步驟中。

種群初始化。個體的所有設計變量在相應的取值范圍內隨機選擇，以構件組為單位，采用基于約束的策略生成最終個體，最大限度地保證初始種群在可行域內均勻分布和算法的全局搜索能力。

適應度評估。采用式（12）計算每個個體的偽目標函數值，進而得到其適應度。

2.3.1 遺傳算法

遺傳算法（Genetic Algorithm，GA）是基于大自然中生物體進化規律，模擬達爾文生物進化論的自然選擇法則和遺傳學機理的生物進化過程思想的一種優化算法，具體為將優化問題以基因的形式對種群中所有個體進行編碼，通過自然選擇、遺傳和變異過程實現新種群的更新迭代，最終獲得適應性高的個體，即最優個體，該方法已被廣泛應用于機器學習、信號處理、組合優化等領域。該算法的主要流程（見圖3）如下。

1）個體編碼。采用實數編碼方式將求解問題轉換為可供遺傳算法進行后續操作的帶有數據信息的染色體或個體，建立問題解空間和算法參數搜索空間的映射關系。

2）選擇算子。根據遺傳算法中“適者生存”的思想，從上一代種群的適應度選擇出優質個體作為交叉和變異操作的基礎。采用輪盤賭策略對個體進行選擇，即通過計算所有個體的適應度，其值越高，則被選擇的概率越大。

3）交叉算子。在荷載作用下，結構構件具有較強的相互作用關系，存在著荷載的分配問題，如應力不僅與該構件的截面尺寸相關，還與其他構件的剛度以及分配的荷載相關，若在所有設計變量之間采用多點交叉，容易導致原本滿足應力要求的構件發生超限的情況，使算法的收斂速度降低等問題。為了提高算法的性能，采用基于構件層次的多點交叉策略，即在每一組構件的4個參數中隨機選擇一個點位進行交叉，突出相同構件組之間父代特性的繼承和遺傳。

4）變異算子。與交叉算子相似，采用基于構件層次的多點變異策略，即在每一組構件的4個參數中隨機選擇一個點位，在其取值范圍內隨機生成，提高對構件組的局部搜索能力，增加種群的多樣性并避免“早熟”現象的發生。

5）終止準則。設置最大迭代次數和最優解保持在誤差范圍內的最大連續次數，當滿足任意一種情況時，優化過程終止，輸出最優解。

2.3.2 改進遺傳算法

經典遺傳算法存在著一些弊端，在基于輪盤賭策略的選擇操作中，迭代后期的個體差異較小，由于適應度相近較難選擇出真正的優質個體，在交叉和變異操作中，概率固定且缺乏搜索方向的引導，對設計變量的取值擾動較大，容易破壞構件層次的優質基因，使算法的局部搜索能力降低，整體未設置精英保留策略，可能造成優質個體基因的浪費。因此，考慮采用適應度尺度變換、基于方向的交叉算子、非均勻變異算子、自適應概率、精英保留策略、重復項替代機制對其進行改進，稱為基于方向的自遺傳算法（genetic algorithm，DBAGA），其主要流程見圖4。

適應度尺度變換[25]。適應度對算法的收斂性有一定的影響，為了在優化初期對少數適應度較高的個體進行控制，降低其與其他個體的差異，以維護種群多樣性，在優化后期適當放大個體之間的差異，提高優質個體的競爭性，采用線性尺度變換策略對適應度進行處理，其數學表達式為

精英保留策略[25]。為了避免精英個體的丟失，提高子代個體對父代個體優質基因的繼承特性，將歷史最優解保存并在每一次迭代過程中用于替代最劣解，可以有效保證最優個體不會被破壞，提高算法的收斂性，但同樣存在某個局部最優解不易被淘汰而使優化過早收斂的問題，因此與重復項替代機制配合使用。

重復項替代機制[26]。由于算法的遺傳特性，經過選擇、交叉和變異操作后，種群中很可能存在重復個體，為了避免重復計算和降低優化時間，用變異后的精英個體來替代重復項，能夠有效增加種群的多樣性，同時提高對精英個體參數取值附近的局部搜索，改善因精英保留策略帶來的過早收斂和陷入局部最優解問題。

2.3.3 多種群遺傳算法

優化算法的性能和結果受到算法中參數的影響，如遺傳算法中的交叉概率等，基于固定參數的優化隨機性較強、魯棒性較差，采用基于多種群的思想可以改善此類問題。在同一次優化中，同時生成多個初始種群或者將整體群體劃分為多個子群體，每個子群體設置不同的算法參數，各自同時進行優化，在一定的迭代次數后，通過移民算子將各子種群在進化過程中出現的最優個體引入相鄰的子種群中，實現種群之間的信息交換。該方法能夠有效降低的單一種群算法的隨機性和提高魯棒性，減少對參數設置的依賴性。對上述GA和DBAGA都進行多種群的設置，即多種群遺傳算法（Multi Population GA，MPGA）和基于方向的多種群遺傳算法（Direction-based MPGA，DMPGA），以MPGA為例進行說明，見圖5。在多種群算法中，各參數值不固定，只給定各自的取值范圍，在每次優化開始時隨機得到。

移民算子。在多種群算法中，將群體劃分為一些子種群，通過移民操作建立子種群之間的相互聯系并實現信息交流，具體步驟如下：設置子種群數、移民間隔（相鄰兩次移民的間隔迭代數）和移民率（每次被移民的個體數量）；每個子種群按一定的模式（即獨立優化器，在圖5中為GA）分別進行獨立優化；當迭代次數滿足移民間隔時，相鄰子種群進行有序的移民操作。如設置子種群數為4，移民間隔為5，移民率為1，則將群體劃分為4個子種群，每個子種群進行獨立優化，每5次迭代時，用子種群1中歷史最優的1個個體替換子種群2中當代最差的1個個體，以此類推，按順序完成所有子種群間的移民操作（2→3，3→4，4→1）。

2.4 自動優化過程

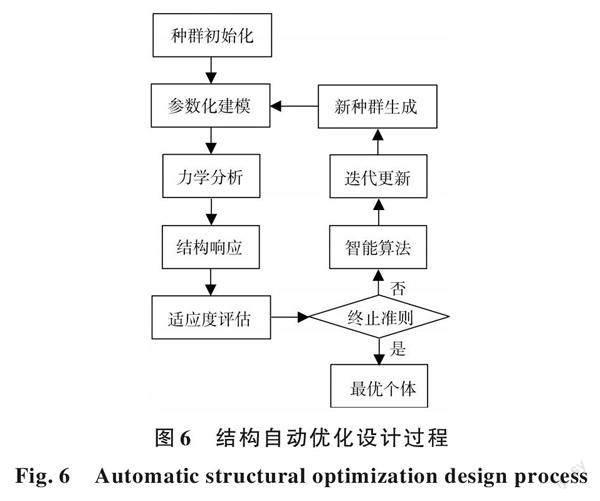
結構體系的自動優化設計過程主要包括結構的有限元分析和智能算法的迭代更新兩步，搭建優化算法框架，通過MSC.Marc有限元軟件完成對初始化種群的力學分析，基于Python二次開發技術對結構的計算結果進行提取和整理，得到個體的適應度，再由優化算法生成新一代種群，基于參數化建模方法和智能算法實現結構設計的反復計算分析和自動尋優過程，見圖6。為了節約結構分析時間，利用多核CPU設置并行計算。

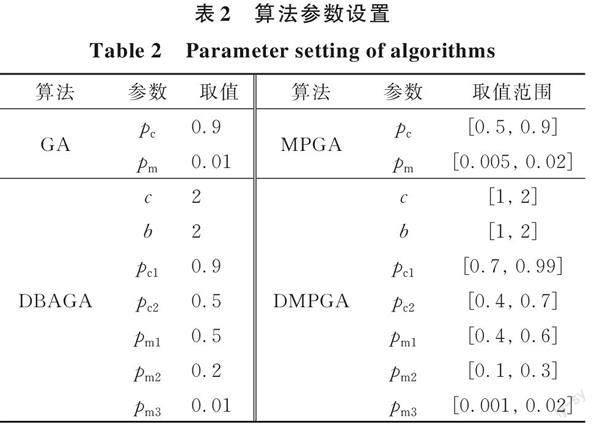
采用4種算法對鋼框架結構進行優化，各進行20次優化，在優化過程中，各算法的參數設置保持不變，具體取值見表2。在2種單種群算法中，因試算后發現種群規模設置較小時會出現過早收斂情況且優化結果不理想，故均設置為100；在2種多種群算法中，移民算子均設置為每1次迭代后進行相應操作，子種群均設置為5個且每個子種群10個個體。

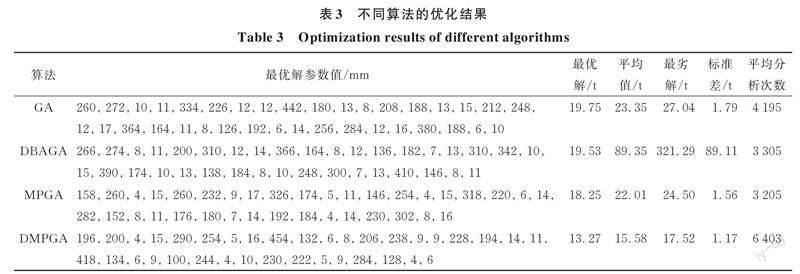
3 結果分析

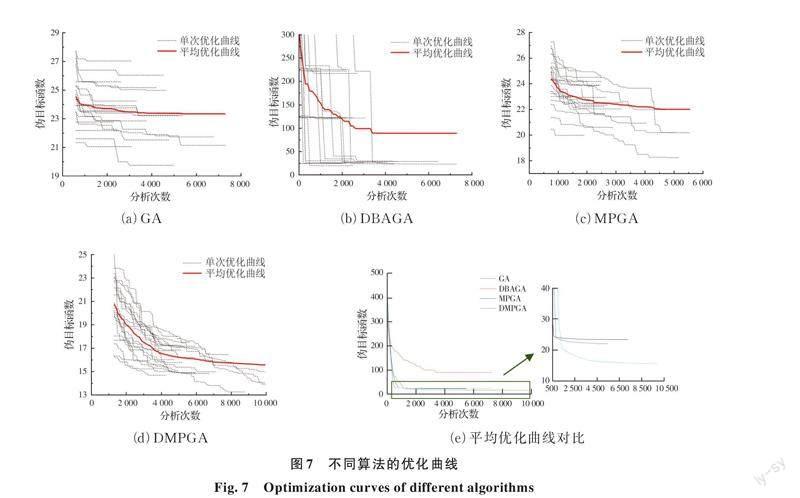
鋼框架結構不同算法的優化曲線和計算結果見圖7、圖8和表3。對于GA，20次優化后的結構均能滿足所有的約束條件，但最優解呈現出較強的離散性，其標準差為1.79 t，其中，最優解和最劣解分別為19.75、27.04 t，差值較大，達到7.29 t。從圖7（a）中可見，大多數優化所需的分析次數在4 000次左右，其中，有6次優化所需的分析次數小于2 800次，計算成本較小，但在1 000次分析后，大多數優化曲線進入平穩階段且后期僅存在1～2次下降，由此說明，該算法容易陷入局部最優解而過早收斂，局部搜索能力較差，這是因為其交叉和變異策略都是針對每個構件組的某一個隨機的基因位進行的相關操作，不確定性較高，缺乏一個搜索方向的引導，容易造成優質基因被破壞。

對于DBAGA，優化后的結構中有8次無法滿足所有的約束條件，由于偽目標函數中考慮了約束條件的影響，因此，受多個最劣解的影響，優化結果的平均值和標準差均較差，分別達到89.35、89.11 t，在該算法參數的設置下呈現出較強的離散性和隨機性。從優化所需的分析次數來說，有14次算例小于3 000次即可達到終止判別條件，計算代價較低，同樣存在容易陷入局部最優解而過早收斂的問題。這是因為該算法的交叉策略是針對設計變量的所有維度，雖然通過較優個體向較差個體提供了搜索方向的引導，但受到算法參數的設置影響，如果交叉的兩個個體都較差，其交叉后的子代個體則有較大可能無法得到好的改善，此外，在迭代后期，由于精英策略保留的歷史最優個體將在種群中重要性增加，即使設置了重復項替代機制對該個體的重復項進行了變異且在其參數取值附近進行了局部搜索，但由于該個體本身質量較差且每一次迭代僅存在少數重復項，算法的局部搜索能力仍不易尋到更優質的解。

對于MPGA，優化后的結構均能滿足所有的約束條件，最優解和最劣解分別為18.25、24.50 t，差值達到6.25 t，但除少數案例以外，其他優化結果相對集中且標準差僅有1.56 t，表現出較大的離散性，但優于GA。從圖7（c）中可見，大多數優化所需的分析次數小于2 700次，計算時間較短，在迭代前期能下降到接近最終解便進入到平穩階段且后期出現下降的次數較GA有所增加，說明算法的局部搜索能力較GA更好，這是因為采用了多種群思想，部分改善了GA存在的局部搜索能力較差的缺點。該算法的基礎是GA，同樣是基于構件組進行的交叉操作，在迭代過程中容易破壞較優個體，缺少搜索方向的引導，大多靠全局搜索來尋優，具有一定的隨機性。

對于DMPGA，優化后的結構均能滿足所有的約束條件，其中，最優解和最劣解分別為13.27、17.52 t，標準差僅有1.17 t，該算法的魯棒性較好。從圖7（d）可見，優化所需的分析次數大多集中于5 000次左右，少數案例進行到了最大迭代次數才終止，受其影響，20次優化所需的平均分析次數達到6 403次，所有的優化曲線表現出較多次的下降，說明該算法的局部搜索能力較強。這是因為DMPGA設置了多個子種群，集合了多個不同參數設置且獨立的DBAGA，極大地降低了單種群算法對其參數取值的依賴性，由于自適應概率和基于方向的交叉算子，每個DBAGA都存在較差個體向較優個體前進的機制，即使其歷史最優解的質量較差，但通過移民算子可以得到極大地改善。

由圖7（e）可見，除DBAGA之外，其他3種算法優化后的結構均能滿足約束條件。其中，GA、DBAGA和MPGA的平均優化曲線分別在約1 000、2 000和1 500次分析后下降到較低水平，優化前期的收斂速度較快，但隨后基本保持平穩狀態，此外，由表3可見，3種算法所需的平均分析次數分別為4 195、3 305、3 205次，整體表現為局部搜索能力不足，存在早期陷入局部最優解而過早收斂的問題。相比之下，DMPGA的平均優化曲線在1 000～3 000次分析中仍有較大幅度的下降，約6 000次分析后進入穩定期，所需的平均分析次數為6 403次，雖然遠高于其他算法，但優化前期和后期均能表現出較好的搜索能力且最終得到的優化結果遠好于其他算法，具體如下：從平均解來說，DMPGA的結果為15.58 t，比GA、DBAGA、MPGA的結果分別低33.3%、82.6%、29.2%；從最優解來說，DMPGA的結果為13.27 t，比GA、DBAGA、MPGA的結果分別低32.8%、32.1%、27.3%；從標準差來說，DMPGA的結果為1.17 t，比GA、DBAGA、MPGA的結果分別低34.7%、98.7%、25.2%；從最劣解來說，DMPGA的結果為17.52 t，比GA、DBAGA、MPGA的最優解都小，分別低11.3%、10.3%、4.0%。因此，由于采用了并行計算技術，平均一次結構分析所用時間約為1～2 s，一次結構優化所需的總體計算時間約為1～4 h，耗時較短，DMPGA在計算效率方面雖有不足和有待改進之處，但在可接受范圍之內，此外，該算法在搜索能力和優化后結構的質量結果方面有明顯的優勢。

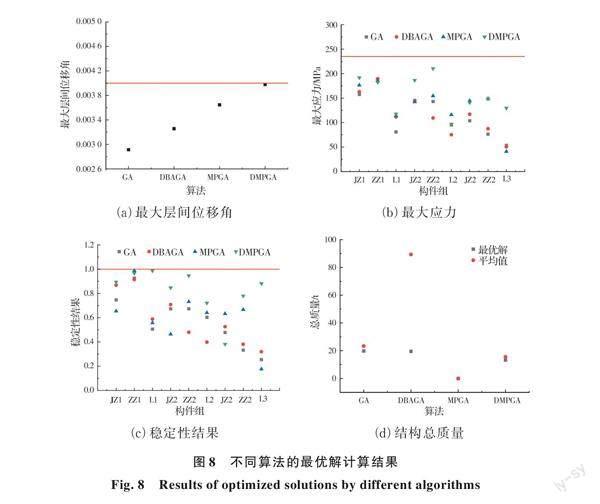
由圖8和表3可見，不同算法的最優解都能滿足約束條件，但最優結構的設計變量參數值和性能指標結果相差較大，這是因為每種算法都是基于遺傳算法的思想，具有一定的隨機性，即使結構總質量相近，但構件尺寸和結構性能仍存在較大差異。與GA和DBAGA相比，總體來說，基于多種群思想的MPGA和DMPGA最優解的結構性能指標更接近限值，兩者相比，DMPGA的結果更好，如最大層間位移角為0.003 98，基本等于限值1/250，多組構件的穩定性結果接近1，說明其優化后的結構更優，既能滿足約束條件，又具有較小的總質量。

總體來說，DBAGA比GA的局部搜索能力更強，這是因為非均勻變異算子和重復項替代機制同時增加了種群的多樣性和歷史最優個體參數取值附近的局部搜索，但優化結果仍較差；基于多種群的算法能夠有效改善基于單種群的算法的隨機性和魯棒性，通過多組不同參數設置降低了優化結果對其的依賴性，如在前面分析中提到的DBAGA可能由于精英策略保留的個體質量較差而不易尋到更優質的解，但通過多種群機制的移民算子，能夠有效建立起子種群之間多個歷史最優解的聯系，有效彌補了單種群算法的不足；與MPGA相比，由于增加了基于方向的交叉算子能夠引導較差個體向較優個體學習，DMPGA具有更強的全局和局部搜索能力。

4 結論

以結構的材料用量最小化為目標，通過罰函數法同時考慮多種結構約束條件，以遺傳算法為基礎，結合鋼框架結構的特征，建立了結構的自動優化設計流程，通過多種策略對算法進行了改進，引入多種群思想，驗證了多種群遺傳算法在鋼框架結構優化問題中的有效性，主要結論如下：

1）與GA相比，DBAGA由于引入了基于方向的交叉算子、非均勻變異算子和重復項替代機制，有效地提高了算法的局部搜索能力，但其優化結果仍較差，多數優化后的結構無法滿足所有的約束條件。

2）基于多種群思想的遺傳算法通過設置多個不同參數的子種群和移民算子，建立起子種群之間的聯系，降低了單種群遺傳算法對參數設置的依賴性，有效地改善了其隨機性較強的問題，提高了算法的魯棒性。

3）基于多種群思想的DMPGA由于存在基于方向的交叉算子、非均勻變異算子、重復項替代機制，其局部搜索能力得到了較大的改善，優化結果的最優解為13.27 t，比GA、DBAGA、MPGA的結果分別低32.8%、32.1%、27.3%。

參考文獻

[1]? 李國強， 陳素文. 從汶川地震災害看鋼結構在地震區的應用[J]. 建筑鋼結構進展， 2008， 10（4）： 1-7， 62.

LI G Q， CHEN S W. From the damage by Wenchuan earthquake to the application of steel building in seismic zone [J]. Progress in Steel Building Structures， 2008， 10（4）： 1-7， 62. （in Chinese）

[2]? 孫得璋， 黃勇， 楊振宇， 等. 九寨溝7.0級地震中典型非結構構件震害特征[J]. 地震工程與工程振動， 2019， 39（1）： 27-34.

SUN D Z， HUANG Y， YANG Z Y， et al. Seismic damages of typical nonstructural components in the MS7.0 Jiuzhaigou earthquake [J]. Earthquake Engineering and Engineering Dynamics， 2019， 39（1）： 27-34. （in Chinese）

[3]? 潘毅， 陳建， 包韻雷， 等. 長寧6.0級地震村鎮建筑震害調查與分析[J]. 建筑結構學報， 2020， 41（Sup1）： 297-306.

PAN Y， CHEN J， BAO Y L， et al. Seismic damage investigation and analysis of rural buildings in MS6.0 Changning earthquake [J]. Journal of Building Structures， 2020， 41（Sup1）： 297-306. （in Chinese）

[4]? 朱杰江， 顧元杰. 高地震烈度區某大高寬比住宅建筑結構優化設計[J]. 建筑結構， 2020， 50（11）： 21-26.

ZHU J J， GU Y J. Optimization design of a residential building with large height-width ratio in high seismic fortification intensity area [J]. Building Structure， 2020， 50（11）： 21-26. （in Chinese）

[5]? 康庭豪， 王青琴， 張浩. 高層住宅混凝土結構優化設計分析[J]. 智能城市， 2020， 6（9）： 32-33.

KANG T H， WANG Q Q， ZHANG H. Optimization design analysis of high-rise residential concrete structure [J]. Intelligent City， 2020， 6（9）： 32-33. （in Chinese）

[6]? PECHORSKAYA S A， GALISHNIKOVA V V， GEBRESLASSIE S B， et al. Structural analysis of high-rise building using ETABS and RSA software [J]. Structural Mechanics of Engineering Constructions and Buildings， 2021， 17（2）： 133-139.

[7]? WANG F， SHI Q X， WANG P. Seismic behaviour of reinforced concrete frame structures with all steel assembled Q195 low yield buckling restrained braces [J]. Structures， 2021， 30： 756-773.

[8]? 秦佳俊， 譚平， 尚繼英， 等. 模塊化鋼框架單元新型盒式連接節點及其設計方法[J]. 土木與環境工程學報（中英文）， 2021， 43（3）： 37-43.

QIN J J， TAN P， SHANG J Y， et al. Design method on inovative box connections of modular steel frame units [J]. Journal of Civil and Environmental Engineering， 2021， 43（3）： 37-43. （in Chinese）

[9]? TALATAHARI S， GANDOMI A H， YUN G J. Optimum design of tower structures using Firefly Algorithm [J]. Structural Design of Tall and Special Buildings， 2014， 23（5）： 350-361.

[10]? ALDWAIK M， ADELI H. Advances in optimization of highrise building structures [J]. Structural and Multidisciplinary Optimization， 2014， 50（6）： 899-919.

[11]? 趙昕， 趙健哲， 馬壯. 基于等增量敏感性的高層建筑結構反向約束優化設計方法研究[J]. 建筑結構學報， 2019， 40（11）： 210-219.

ZHAO X， ZHAO J Z， MA Z. Reversely constrained optimal design method for tall buildings based on constant incremental sensitivity [J]. Journal of Building Structures， 2019， 40（11）： 210-219. （in Chinese）

[12]? LI Y， DUAN R B， LI Q S， et al. Wind-resistant optimal design of tall buildings based on improved genetic algorithm [J]. Structures， 2020， 27： 2182-2191.

[13]? DEGERTEKIN S O， HAYALIOGLU M S， GORGUN H. Optimum design of geometrically non-linear steel frames with semi-rigid connections using a harmony search algorithm [J]. Steel & Composite Structures， 2009， 9（6）： 535-555.

[14]? GHOLIZADEH S， SHAHREZAEI A M. Optimal placement of steel plate shear walls for steel frames by bat algorithm [J]. The Structural Design of Tall and Special Buildings， 2015， 24（1）： 1-18.

[15]? GHOLIZADEH S， POORHOSEINI H. Seismic layout optimization of steel braced frames by an improved dolphin echolocation algorithm [J]. Structural and Multidisciplinary Optimization， 2016， 54（4）： 1011-1029.

[16]? TALATAHARI S， GANDOMI A H， YANG X S， et al. Optimum design of frame structures using the Eagle Strategy with Differential Evolution [J]. Engineering Structures， 2015， 91： 16-25.

[17]? ?ARBA? S. Optimum structural design of spatial steel frames via biogeography-based optimization [J]. Neural Computing and Applications， 2017， 28（6）： 1525-1539.

[18]? KAVEH A， KHODADADI N， AZAR B F， et al. Optimal design of large-scale frames with an advanced charged system search algorithm using box-shaped sections [J]. Engineering with Computers， 2021， 37（4）： 2521-2541.

[19]? FARSHCHIN M， MANIAT M， CAMP C V， et al. School based optimization algorithm for design of steel frames [J]. Engineering Structures， 2018， 171： 326-335.

[20]? FARSHCHIN M， CAMP C V， MANIAT M. Optimal design of truss structures for size and shape with frequency constraints using a collaborative optimization strategy [J]. Expert Systems with Applications， 2016， 66： 203-218.

[21]? 駱清國， 趙耀， 桂勇， 等. 基于多種群協同進化免疫多目標優化算法的百葉窗優化研究[J]. 兵工學報， 2019， 40（4）： 689-696.

LUO Q G， ZHAO Y， GUI Y， et al. Research on optimization of louvered fin with hybrid multi-objective optimizations based on EDA and AIS [J]. Acta Armamentarii， 2019， 40（4）： 689-696. （in Chinese）

[22]? 張天佳， 楊永勝. 基于并行結構的多種群粒子群優化算法[J]. 傳感器與微系統， 2020， 39（9）： 119-121.

ZHANG T J， YANG Y S. Multi-swarm PSO algorithm based on parallel structure [J]. Transducer and Microsystem Technologies， 2020， 39（9）： 119-121. （in Chinese）

[23]? 建筑抗震設計規范： GB 50011—2010 [S]. 北京： 中國建筑工業出版社， 2010.

Code for sesmic design of buildings： GB 50011—2010 [S]. Beijing： China Architecture & Building Press， 2010. （in Chinese）

[24]? 鋼結構設計標準： GB 50017—2017 [S]. 北京： 中國計劃出版社， 2018.

Standard for design of steel structures： GB 50017—2017 [S]. Beijing： China Architecture & Building Press， 2017. （in Chinese）

[25]? 王小平， 曹立明. 遺傳算法： 理論、應用與軟件實現[M]. 西安： 西安交通大學出版社， 2002.

WANG X P， CAO L M. Genetic algorithm： Theory， application and software implementation [M]. Xi，an： Xi，an Jiaotong University Press， 2002. （in Chinese）

[26]? 王吉權， 程志文， 張攀利， 等. 求解有約束優化問題的實數遺傳算法改進研究[J]. 控制與決策， 2019， 34（5）： 937-946.

WANG J Q， CHENG Z W， ZHANG P L， et al. Research on improvement of real-coded genetic algorithm for solving constrained optimization problems [J]. Control and Decision， 2019， 34（5）： 937-946. （in Chinese）

[27]? 周明， 孫樹棟. 遺傳算法原理及應用[M]. 北京： 國防工業出版社， 1999.

ZHOU M， SUN S D. Genetic algorithms： theory and applications[M]. Beijing： National Defense Industry Press， 1999. （in Chinese）

（編輯? 胡玲）

DOI： 10.11835/j.issn.2096-6717.2022.071

收稿日期：2022?01?30

基金項目：國家自然科學基金（52130801）；重慶市博士后研究項目（2021XM2039）

作者簡介：周俊文（1991- ），男，博士，助理研究員，主要從事結構優化設計研究，E-mail：0zhoujunwen0@cqu.edu.cn

通信作者：劉界鵬（通信作者），男，教授，博士生導師，E-mail：liujp@cqu.edu.cn。

Received： 2022?01?30

Foundation items： National Natural Science Foundation of China （No. 52130801）; Chongqing Postdoctoral Science Foundation （No. 2021XM2039）

Author brief： ZHOU Junwen （1991- ）， PhD， research assistant， main research interest： structural optimization design， E-mail： 0zhoujunwen0@cqu.edu.cn.

corresponding author：LIU Jiepeng （corresponding author）， professor， doctorial supervisor， E-mail： liujp@cqu.edu.cn.