車體偏載對系列化標準地鐵80B車輛動力學性能的影響研究

楊陳,胡定祥,賈小平,2,孫海東

(1.中車南京浦鎮車輛有限公司 技術中心,江蘇 南京 210031;2.西南交通大學 牽引動力國家重點實驗室,四川 成都 20180)

良好的車輛動力學性能是軌道車輛設計持續追求的目標[1-2]。地鐵車輛頻繁地上下客,以及乘客的不均勻分布,將導致車體出現偏載,進而導致車輛動力學性能發生強烈變化[3-4]。池茂儒等[5]研究了偏載對車輛平穩性的影響趨勢,發現隨著偏載的增大,車輛的整體平穩性逐漸變差,縱向偏載將引起車輛前后端的平穩性產生較大的差距。馮陳程等[6]在靜力分析的基礎上,建立了C80 型重載貨車的動力學模型,計算了貨車在不同偏載狀態下通過曲線時的脫軌系數和輪重減載率,研究發現隨著偏載的增大,貨車的運行安全性逐漸降低。夏張輝等[7]建立包含車體彈性及車下設備的高速動車組精細化剛柔耦合動力學模型,研究了車下設備偏心對整車振動性能的影響及其機理,發現車下設備偏心會使車下設備6個方向自由度的振動發生耦合現象,導致各階剛體振型及振型頻率產生較大變化,致使車下設備減振效果降低、車輛運行平穩性變差。本文建立考慮車體偏載的理論模型,理論分析車體偏載對車體剛體振型頻率的影響規律;建立車輛系統動力學模型,計算分析車體偏載對車輛動力學性能指標的影響。研究結果可為系列化標準地鐵80B車體偏載控制及相關規范的制定提供理論依據。

1 理論模型

本文將車體考慮為具有6個自由度的空間剛體,將空氣彈簧考慮為具備三向剛度的彈簧[8],建立圖1所示坐標系。車體坐標系的定義[9]為:車體的重心位置為坐標原點,以車輛走行方向為x正方向,車輛走行方向水平向右為y正方向,垂直向下為z正方向,側滾rx、點頭ry、 搖頭rz正方

圖1 車體坐標系示意圖

向按右手法則確定。

第i個(i=1,2,3,4)空氣彈簧的位置坐標為(ai,bi,ci),其三向剛度為(kxi,kyi,kzi),當車體振動時,第i個空氣彈簧產生的力與力矩分別為:

(1)

式中:[x,y,z,rx,ry,rz]為車體6個自由度的剛體位移。4個空氣彈簧產生的總的力與力矩為:

(2)

當不考慮外界激勵時,建立車體6個自由度的動力學方程:

(3)

式中:M為車體的質量矩陣,其表達式為:

M=diag(m,m,m,Ixx,Iyy,Izz)

(4)

式中:m為車體質量;Ixx、Iyy、Izz分別為車體繞對應軸的轉動慣量。

將式(3)展開并整理得:

(5)

根據式(3),求解車體6階剛體模態振型向量及模態頻率,有

KTj=λjMTj,j=1,2,3,4,5,6

(6)

式中:Tj=[x,y,z,rx,ry,rz]jT為各階模態振型向量6個自由度的剛體位移;λj=(2πfj)2為各階模態特征值;fj為各階模態頻率;K為剛度矩陣。

2 模態參數計算分析

依據第1章所建理論模型,以系列化標準地鐵80B車輛為計算參數,估計乘客平均體重為75 kg,分析乘客在車內的不均勻分布引起的車輛重心縱向與橫向的偏移對車體剛性振型頻率的影響。若10～20名乘客因上下車集中站立在車體一側端部,可引起縱向偏載1 m左右,圖2為縱向偏載對系統橫態影響。可以看到,隨著縱向偏載量增大,車體搖頭、車體點頭模態頻率增大,車體浮沉、車體下心滾擺模態頻率減小,而車體上心滾擺模態頻率基本不變。若10～15名乘客因單側車門上下,坐立在車體一側, 可引起橫向偏載0.05 m左右。圖3為橫向偏載對系統模態影響。從圖3可以看到,橫向偏載時,隨著偏載量增加,車體下心滾擺、車體搖頭、車體浮沉、車體上心滾擺、車體點頭模態頻率基本不變。圖4和圖5分別為乘客車內不均勻分布時,縱向和橫向的同向偏載與反向偏載對系統模態的影響。可以看到,縱向和橫向的同向偏載(此時縱向偏載dx與橫向偏載dy設置為dy=0.05dx)與反向偏載 (此時縱向偏載dx與橫向偏載dy設置為dy=-0.05dx)變化,對車體下心滾擺、車體搖頭、車體浮沉、車體上心滾擺、車體點頭模態頻率的影響與單一的縱向偏載變化的影響一致。

圖2 縱向偏載對系統模態影響

圖3 橫向偏載對系統模態影響

圖4 縱向和橫向同向偏載對系統模態影響

圖5 縱向和橫向反向偏載對系統模態影響

3 動力學性能指標計算分析

采用系列化標準地鐵80B車輛動力學參數,建立地鐵車輛動力學模型,見圖6。車輪踏面外形采用LM踏面,鋼軌采用R60鋼軌,輪對內側距為1 353 mm,軌底坡為1∶40,軌距為1 435 mm,軌道譜采用美國5級譜[10-11],計算分析車體偏載對車輛臨界速度、輪軸橫向力、脫軌系數、輪重減載率以及運行平穩性指標的影響[12-14]。其中,輪軸橫向力、脫軌系數、輪重減載率為車輛以80 km/h速度通過450 m半徑曲線時的計算結果,縱向偏載計算范圍為[-3 m,3 m],橫向偏載計算范圍為[-0.15 m,0.15 m]。

圖6 地鐵車輛動力學模型

圖7所示為車體偏載對臨界速度的影響。可以看出,橫向偏載對臨界速度影響較小,而縱向偏載、縱向和橫向同向偏載及二者反向偏載均對臨界速度有影響,臨界速度隨著重心的前移而逐漸增加,總體而言,在偏載計算范圍內,臨界速度仍然大于120 km/h。圖8～圖10所示分別為車體偏載對輪軸橫向力、脫軌系數及輪重減載率(一位輪對最大值)的影響,可以看出, 車體橫向偏載會略微影響輪軸橫向力;車體縱向偏載和橫向偏載對脫軌系數影響較大,隨著重心的單獨縱向前移,一位輪對(右側車輪)脫軌系數逐漸降低,而隨著重心的單獨橫向水平右移,脫軌系數逐漸增加;隨著車體縱向偏載和橫向偏載的增加,輪重減載率(一位輪對最大值)大致呈逐漸增大趨勢;總體而言,在偏載計算范圍內,上述3種曲線通過指標仍滿足要求[15]。

圖7 車體偏載對臨界速度的影響

圖8 車體偏載對輪軸橫向力的影響

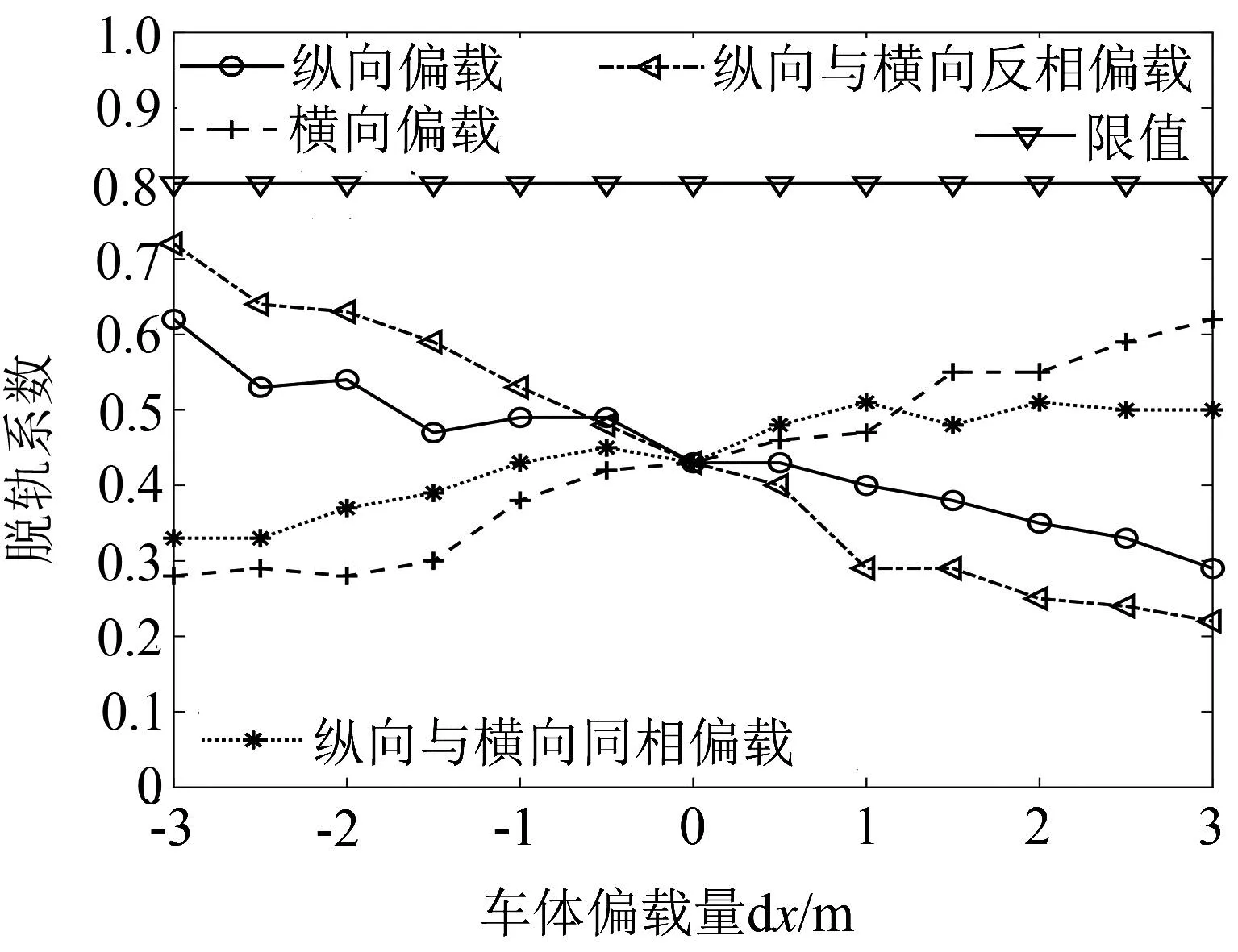
圖9 車體偏載對脫軌系數的影響

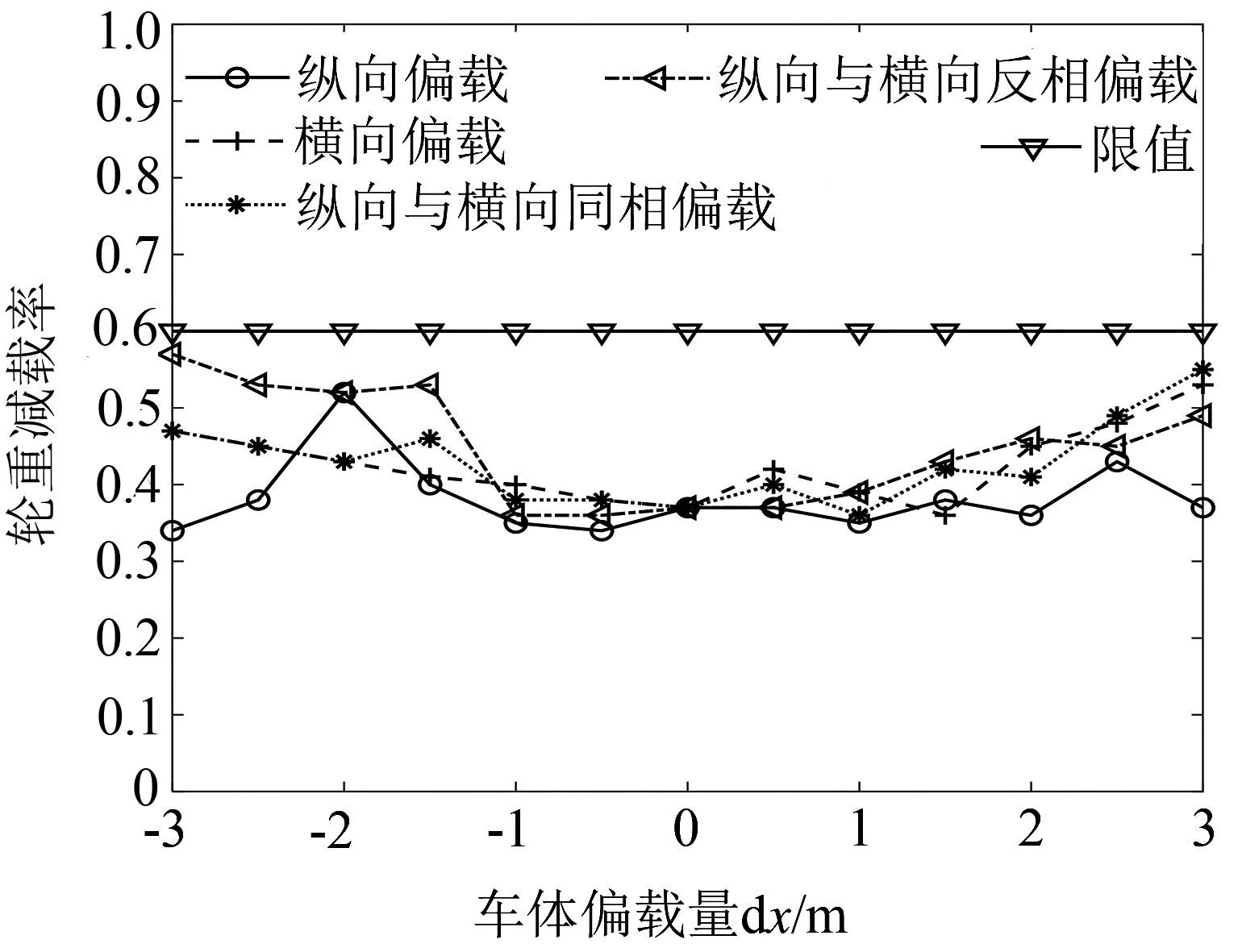
圖10 車體偏載對輪重減載率的影響

圖11為車體偏載對橫向運行平穩性指標的影響。這里分別考慮了前后轉向架上方車體左右兩側各1 m的平穩性指標評價位置的計算結果。 可以看出, 車體橫向偏載在計算范圍內對橫向平穩性影響較小,這也符合圖3橫向偏載對車體模態頻率產生較小的影響規律一致。總體來說,縱向偏載發生后,減載端轉向架橫向平穩性指標會增加。

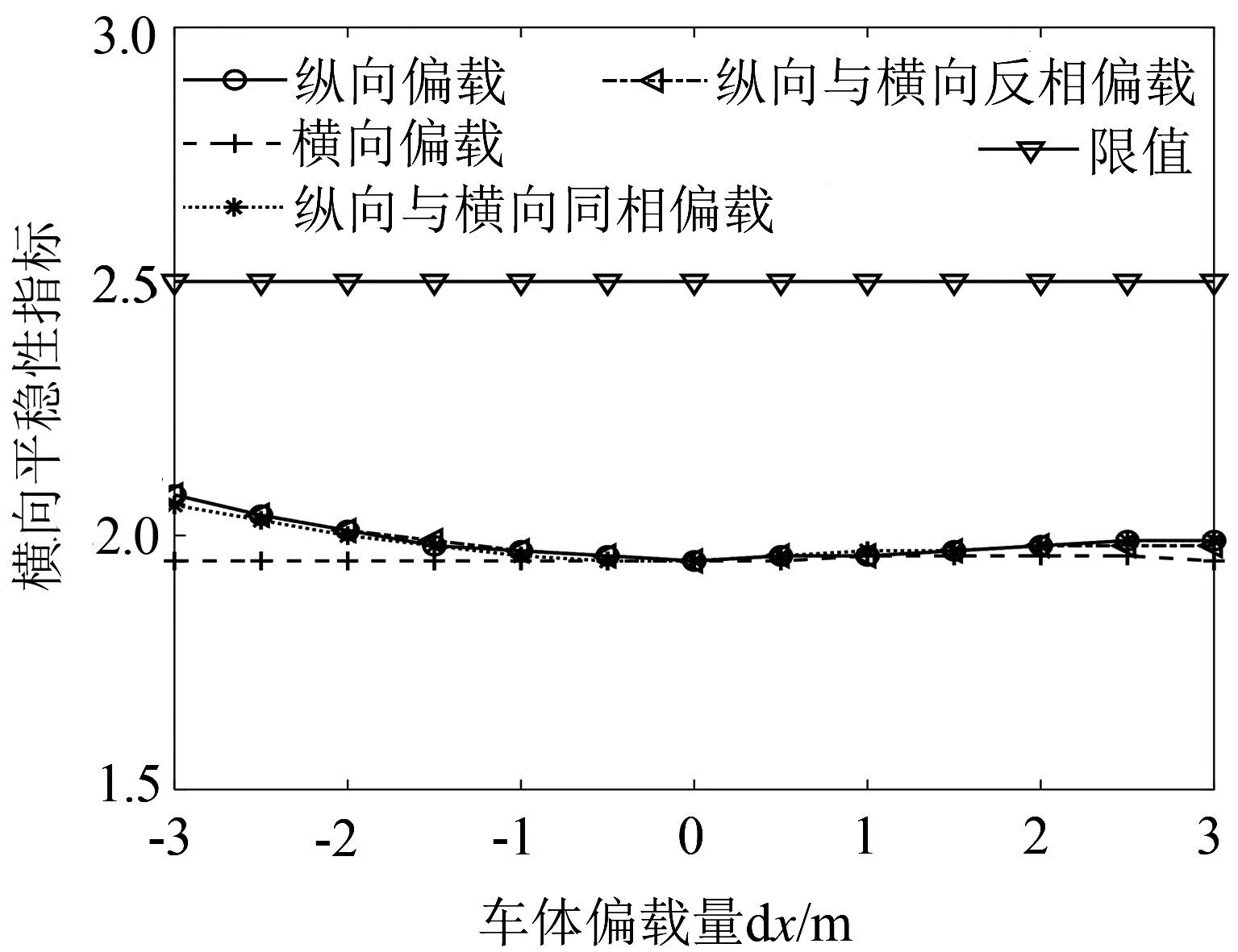
(a)車體前左

(b)車體前右

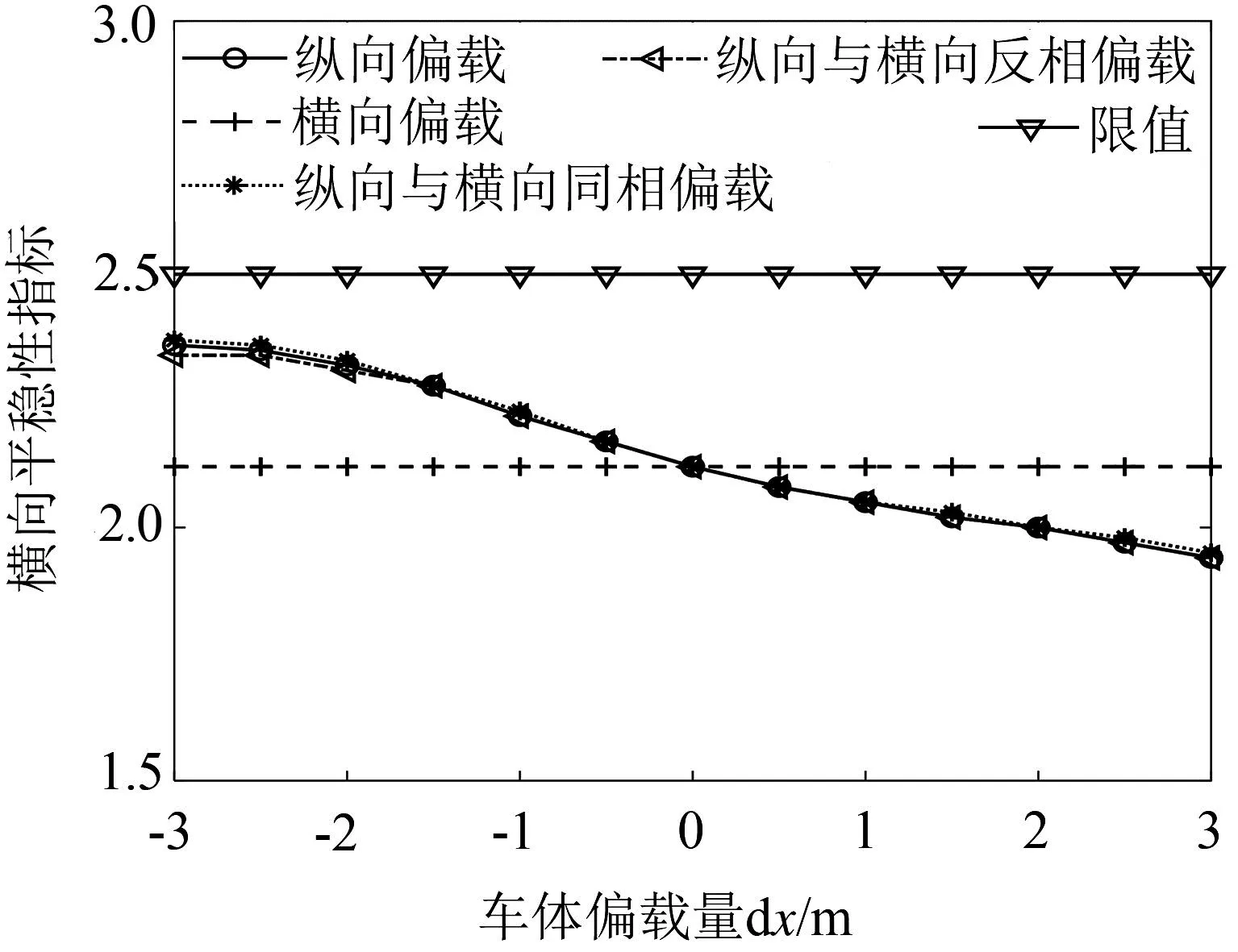
(c)車體后左

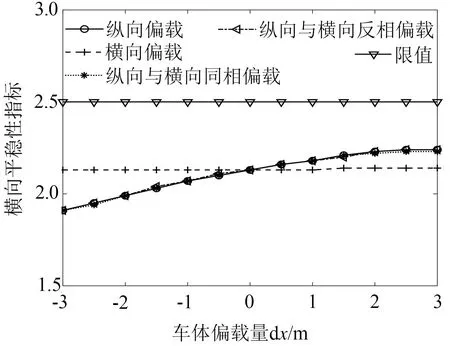
(d)車體后右圖11 車體偏載對橫向平穩性指標的影響

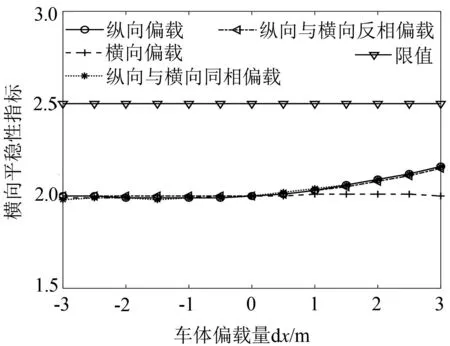
圖12給出了車體偏載對垂向運行平穩性指標的影響規律。可以看出,車體偏載對垂向運行平穩性指標的影響規律與橫向相似。結合第2章偏載對模態頻率的影響不難發現,縱向偏載對車體的模態頻率影響更大,進而對車輛橫向及垂向運行平穩性的影響更大;總體而言,縱向偏載發生后,減載端轉向架垂向平穩性指標會增加。

(a) 車體前左

(b) 車體前右

(c) 車體后左

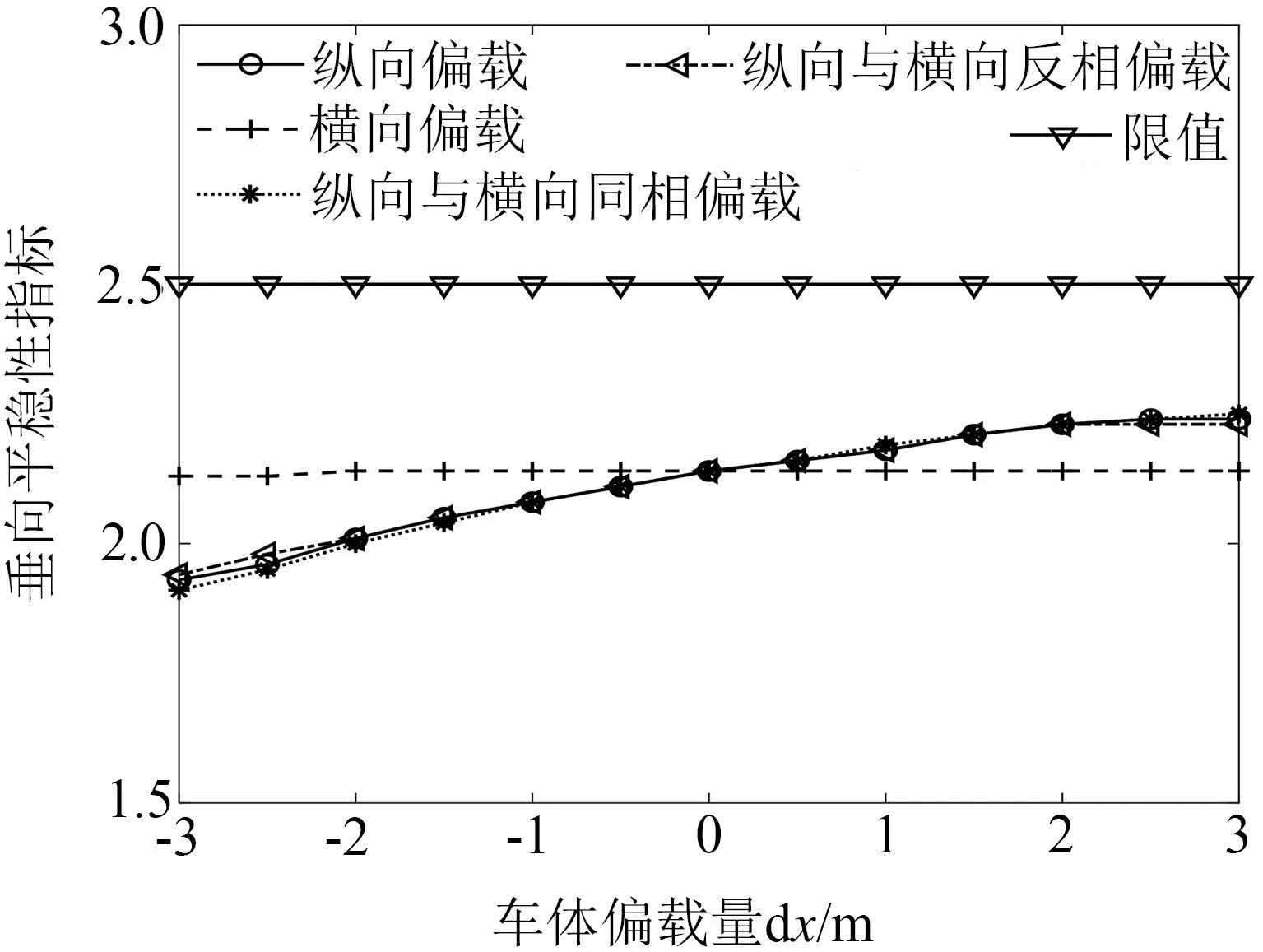
(d) 車體后右圖12 車體偏載對垂向平穩性指標的影響

4 結論

(1)隨著縱向偏載量增大,車體搖頭、車體點頭模態頻率增大,車體浮沉、車體下心滾擺模態頻率減小,而車體上心滾擺模態頻率基本不變;橫向偏載在[-0.15 m,0.15 m]范圍內變化時,車體下心滾擺、車體搖頭、車體浮沉、車體上心滾擺、車體點頭模態頻率基本不變。

(2)車體橫向偏載在[-0.15 m,0.15 m]范圍內對臨界速度影響較小,而縱向偏載對臨界速度有影響,臨界速度隨著車體重心的前移而逐漸增加。橫向偏載會略微影響輪軸橫向力;縱向偏載和橫向偏載對脫軌系數影響較大,隨著偏載縱向前移,一位輪對(右側車輪)脫軌系數逐漸降低,而隨著偏載橫向水平右移,脫軌系數逐漸增加;隨著車體縱向偏載和橫向偏載的增加,輪重減載率(一位輪對最大值)大致呈逐漸增大趨勢。

(3)縱向偏載對車體的模態頻率影響較大,進而對車輛橫向及垂向運行平穩性的影響更大;總體而言,縱向偏載發生后,減載端轉向架垂向平穩性指標會增加。