投資成本和發電系統可靠性提升水平間的量化分析方法

李 琛，孫 悅，羅金嵩，魏 揚，徐 晶，陳博文

（中國長江電力股份有限公司，湖北 宜昌 443133）

水力發電廠作為清潔能源，具有污染小、可再生、成本低等特點，受到了各國的廣泛關注。“雙碳”目標下，風、光等新能源在我國電力系統的滲透率不斷提高，將成為電力系統的主導電源[1]。在此背景下，水力發電廠作為調峰調頻的重要角色，研究其出力可靠性具有重要意義。眾所周知，提高發電系統可靠性勢必意味著增加投資成本。然而，目前還沒有一個準確的數學模型來刻畫投資成本與設備故障率降低水平間的不確定性關系，進而量化投資成本對發電系統可靠性的影響。

已有研究學者所建立的投資成本和電力系統可靠性間的函數關系未考慮投資成本對設備故障率的不確定性影響[2，3]。然而，由于不同廠家或設備制造等原因，會導致同一投資成本下的設備故障率降低水平不同，從而給水力發電系統帶來潛在的風險，也會給電廠成本控制人員和運行方式人員帶來一定的誤導。

因此，本文建立了投資成本和發電系統可靠性間的映射關系，定量分析投資成本對發電系統可靠性的影響。首先，提出基于Sigmoid 云模型的投資成本和設備故障率降低百分比間的量化曲線，以刻畫復雜因素影響下的投資成本和設備故障率降低水平間的不確定映射關系，并采用粒子群算法計算Sigmoid 函數云模型的參數。然后，采用K-means聚類算法對同一投資成本下的故障率參數進行聚類，提出一種快速可靠性評估方法，從而建立了投資成本和發電系統可靠性間的精確數學模型，進而定量刻畫投資成本對發電系統可靠性的影響。

1 設備故障率不確定性建模

多年統計數據發現，同一投資成本下，由于可以選擇不同的廠家，或者是設備制造自身的原因，設備可靠性的提升效果往往不同。而且，過高或過低的投資成本，會使設備可靠性提升的不確定性增加，從而影響發電系統可靠性。因此，本文提出設備故障率降低百分比指標HI 來量化投資成本對設備故障率降低水平的不確定性，具體步驟如下：

假設考慮投資成本Pj對設備故障率降低百分比不確定性影響后的故障率記為λi，此時對應的設備故障率降低百分比指標為HIPj。為了模擬投資成本變化時HIPj的變化情況，本文將投資成本P和HI之間的不確定映射關系描述為：

當Pj時，HIPj=0，其隨機故障率沒有額外的不確定性變化；

當0＜Pj＜Pmax時，0＜HIPj＜0.4，隨著投資成本的升高，設備故障率在降低時受其他非成本因素影響的概率越低，HIPj呈現緩慢降低→加速降低→緩慢降低的趨勢。

因此，本文的重點是尋找一種可以表征Pj和HIPj不確定性關系的模型。云模型利用一個具有穩定傾向的隨機數來代替精確隸屬度，既體現了隨機性，也考慮了模糊性，通過二者的結合，形成定性和定量關系之間的映射，成為研究不確定性知識的重要方法[4]。但是，Pj和HIPj之間的映射關系不符合正態分布規律，傳統的正態云模型已不再適用。因此，為了能夠較準確刻畫Pj和HIPj之間的關系，需要建立新的云模型。

Sigmoid 函數是一個在生物學中常見的S型函數[5]，該函數將不同Pj映射為（0，1）區間下的實數，可以較好地擬合投資成本和設備故障率降低水平之間的不確定映射關系，這個實數即為HI指標。為了更加準確的擬合Pj和HIPj之間的映射關系，本文提出一種改進的Sigmoid 函數，表達式如下：

式中，w參數刻畫函數的陡峭程度，w越大，表示函數在Pj附近HI指標的變化越大；b參數刻畫函數在縱軸上的偏移程度，b越大，表示同一投資成本下的HI指標越小。

Sigmoid 函數的云圖可以由云模型的四個數字特征來體現：陡峭程度期望值Ea，偏移程度期望值Eb，熵En和超熵He。因此，Sigmoid 函數云圖是由分布在該函數周圍的散點組成的，其數字特征具體介紹如下：

陡峭程度期望值Ea：刻畫函數在同一投資成本附近下HI的變化程度，即決定函數在橫軸上的分布形狀，是最能代表定性概念的點之一，w～N（Ea，En’）。

偏移程度期望值Eb：刻畫函數在同一投資成本下HI的偏移程度，即決定函數在縱軸上的分布位置，是最能代表定性概念的點之一，b～N（Eb，En’）。

熵En：反應HI的隨機性和模糊性，一般熵越大，隨機性和模糊性也越大。即En刻畫了Ea和Eb的不確定性程度，代表定性概念的可度量粒度以及度量定性概念的不確定性，En’=N（En，He）。

超熵He：超熵是熵的不確定性的度量，是熵的熵，由熵的隨機性和模糊性決定，反應了同一投資成本下HI的凝聚性，一般超熵越大，HI離散程度越大。

Sigmoid 函數云模型圖中的每一個點，就代表一個HI不確定性云滴，即代表投資成本Pj下用戶HIPj的度量。

2 基于改進Sigmoid 函數云模型的設備故障率降低百分比指標分析

為了評估HI相對投資成本的變化程度，需要構建表征不同投資成本下用戶設備故障率降低百分比的云模型，再基于該云模型，預測用戶的HI。因此，本文先根據逆向云發生器，計算Ea、Eb、En、He，然后再根據正向云發生器，得出每一個投資成本Pj下的HIPj。

（1）Sigmoid 函數云模型數字特征計算

首先，根據各個廠家收集得到S組不同投資成本PjS下的HI HISP（js=1，2，3， …，S），將S組（PjS，HISP）j作為逆向云發生器的輸入，來計算Sigmoid 函數云模型數字特征：Ea、Eb、En、He，如圖1 所示。

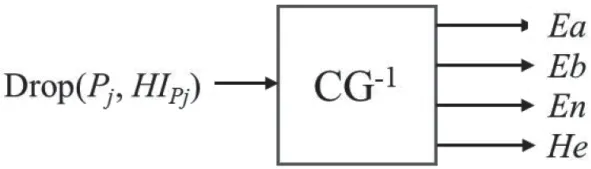
圖1 逆向云發生器

不同于傳統正態云模型數字特征的計算，Sigmoid 函數云模型中的數字特征難以直接通過計算得到，因此，本文采用粒子群算法[6]來計算Ea、Eb、En、He，具體步驟為：

本文用m表示粒子群算法中第m個粒子，m=1，2，…，M；n表示第n個參數，n=1，2，3，4 分別代表參數Ea、Eb、En、He；k、kmax分別代表當前迭代次數和最大迭代次數；xmax、vmax分別代表粒子位置和速度的最大值；xmin、vmin分別代表粒子位置和速度的最小值。具體計算步驟如下：

步驟1：初始化種群：在粒子取值范圍[xmin，xmax]、[vmin，vmax]內分別隨機抽取M組粒子，設定最大迭代次數kmax，并令k=0。

步驟2：局部最優和全局最優變量初始化計算：

首先根據公式（1）計算每一個粒子對應的HI值，即HI（x0（m，：），PjS）（m=1，2，…，M；j=1，2，3），并依據式（4）求解對應的適應度函數值：

假設Erkg=min（Erkm），選取Erkg對應的xkgn作為局部最優值，記為Lgn，并作為初始化全局最優值Ggn，其中，n=1，2，3，4。

步驟3：粒子選取：根據式（5）和（6）更新速度變量vk+1和位置變量xk+1。

式中，c1、c2為常數；u1、u2為[0，1]間的均勻分布隨機數。

步驟4：計算第k+1 次迭代的所有粒子的適應度函數，若＜，則更新局部最優值Ign=。

步驟5：若=min（），得到第k+1 次迭代的全局最優值，若＜，則全局最優值更新為Ggn=。

步驟6：判斷是否達到最大迭代次數kmax，若達到，則停止迭代，根據當前全局最優值得到Sigmoid函數云模型的四個數字特征Ea、Eb、En、He。否則，令k=k+1，轉到步驟3 繼續迭代。

（2）設備故障率降低百分比指標分析

基于上述方法計算得到的云模型數字特征Ea、Eb、En、He，進而根據圖2 所示的正向云發生器，得到不同投資成本Pj下的HIHIPj。具體步驟為：

圖2 正向云發生器

步驟1：根據En’=N（En，He）生成正態隨機數En’；

步驟2：根據w～N（Ea，En’）生成正態隨機數w；

步驟3：根據b～N（Eb，En’） 生成正態隨機數b；

步驟4：通過公式（1）計算投資成本Pj下HIHIPj。

可以發現，對于同一投資成本Pj，根據Sigmoid 函數云模型得到的HIPj每次都是不同的，重復步驟1 到步驟4，根據大數定律，即可得到同一投資成本Pj下，HIPj的云圖。因此，本文提出的改進Sigmoid 函數云模型可以很好的量化同一投資成本下的HI變化程度。

（3）考慮投資成本對設備故障率變化不確定性的可靠性評估方法

結合上述分析，HI和投資成本緊密結合在一起。因此，HI在發電系統可靠性評估中起著至關重要的作用，該指數會改變設備故障率，從而影響發電系統的可靠性。本文假定每次抽樣的系統狀態及負荷大小保持不變。采用非時序蒙特卡洛法來進行電力系統可靠性評估，考慮負荷損失概率LOLP和期望未供電能量EENS指標[7]，可靠性評估步驟為：

步驟1：記當前累計抽樣產生的系統狀態的數目為N；記系統狀態St的削負荷標志為Pf；記系統狀態St的削負荷量為h（St）。令N=1，Pf=0，h（St）=0；

步驟2：根據投資成本Pj，結合設備故障率降低百分比指標模型，抽取相應成本下的設備故障率，再隨機抽取機組狀態，根據各機組容量得到當前迭代次數的系統總發電容量VT；

步驟3：比較峰值負荷PL與步驟3 得到的總發電容量VT；若PL＞VT，Pf=Pf+1，則該系統狀態的削負荷量h（St）=PL-VT，否則，Pf=0，h（St）=0。并令N=N+1；

步驟4：計算各指標的方差系數，若方差系數達到預設的收斂閾值，則停止模擬，轉步驟；否則，轉步驟3 繼續迭代。

步驟5：根據式、統計可靠性指標，輸出計算結果。

步驟2 中，本文采用K-means 聚類方法[8]聚類同一投資成本下的故障率，根據每一類的聚類中心和概率，來抽取相應成本下的故障率，該方法在保證計算精度的前提下，大大的減少了可靠性評估計算時間。因此，經過上述方法，本文在考慮投資成本對設備故障率降低百分比水平不確定性前提下，可建立發電系統可靠性指標和投資成本之間的定量函數關系，可以方便得到不同投資成本下，系統可靠性指標的變化量。

3 算例分析

本文選用IEEE-RTS79 測試系統[9]來進行算例分析。IEEE-RTS79 系統包括32 臺發電機，系統總裝機容量為3 405 MW，年峰值負荷為2 850 MW。假設各元件的運行和維修狀態持續時間呈指數分布。

圖3 展示了設備故障率降低百分比指標的Sigmoid 云圖。黑色的線是經過標幺化后的歷史數據（假設投資成本的基準值為4×108元），灰色的點是通過本文提出的Sigmoid 函數云模型得到的數據。從圖3 可以看出，同一投資成本P對應的HI具有不同的值。

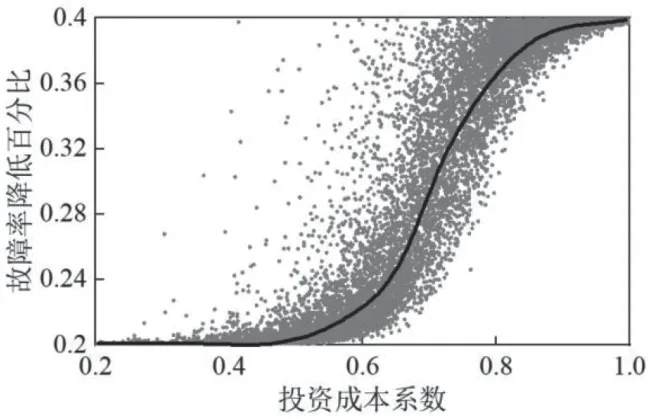
圖3 設備故障率降低百分比不確定性云圖

為了驗證本文所提投資成本和發電系統可靠性提升水平間的量化分析方法的正確性，基于IEEERTS79 系統設計了4 個對比算例，分別計算其可靠性評估指標LOLP、EENS，結果如表1 所示：

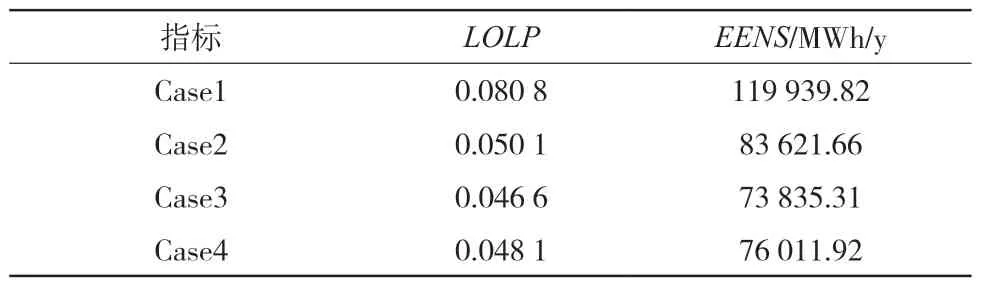
表1 可靠性評估對比結果一

Case1：不考慮投資成本的影響。

Case2：考慮投資成本對設備故障率降低百分比的影響，但不考慮其不確定性。

Case3：基于Sigmoid 云模型考慮投資成本對設備故障率降低百分比不確定性的影響。

Case4：基于歷史數據考慮投資成本對設備故障率降低百分比不確定性的影響。

從表1 可以看出，與不考慮投資成本影響的情況相比，考慮投資成本影響的情況下的可靠性指標顯著下降。其背后的原因是投資成本使得設備故障率降低，進而提高了系統的可靠性水平。本文提出的方法考慮了投資成本對設備故障率降低百分比的不確定性，得到了更合理的可靠性評估結果。

由圖3 可知，對于每一個投資成本P對應的HI均有多種情況，從而會得到不同的隨機故障率曲線，進而會影響到可靠性指標的收斂情況，最終影響系統可靠性評估時間。因此，本文選擇將設備故障率進行聚類，再進行可靠性評估，從而可以加快可靠性收斂速度。為了說明K-means 聚類算法能夠加速系統可靠性評估速度，本文設置了Case5 與Case3對比，結果如表2 所示。

表2 可靠性評估對比結果二

Case5：基于Sigmoid 云模型考慮投資成本對設備故障率降低百分比的影響，且用K-Means 對同一投資成本下的故障率進行聚類。

從表2 可以很直觀看出：對于RTS 系統，Case5的可靠性評估時間大大減少；而且，從表2 可以得到Case3 和Case5 的LOLP 和EENS 相差不大，二者的相對差值分別為0.41%、0.9%，在誤差允許范圍之內。因此，可以得出結論：采用K-Means 算法對同一投資成本下的故障率進行聚類，在保證計算精度的情況下，大大縮短了可靠性評估時間。

4 結語

投資成本增加有降低設備故障率的作用，會使得系統可靠性升高；但是，往往投資成本對于設備故障率的降低是不確定的，受到諸如環境因素、設備廠商等眾多因素的影響，這些因素應該計及在可靠性評估模型中，因此，本文所提出的考慮投資成本對設備故障率降低水平不確定性的可靠性評估結果更加準確。